一道圆锥曲线模拟题的命制与思考
2020-11-15广东潘敬贞
广东 潘敬贞
解析几何是高中数学的核心内容,也是高考命题的重点内容.圆锥曲线解答题常以中档题或压轴题的形式出现,该题重点考查运用代数方法研究几何问题,涉及的内容主要包括平面几何的性质、直线方程、韦达定理、点到直线的距离公式、分类讨论等解析几何的核心内容.该题的解答综合考查学生的推理论证能力、运算求解能力、分析与解决问题能力、考查化归与转化思想,考查学生直观想象、逻辑推理、数学运算等数学核心素养.圆锥曲线解答题也是高考模拟考试必考的题目之一.本文就2018年汕头市第二次模拟考试的圆锥曲线解答题的命制及思考与同行交流.
一、试题与解答赏析
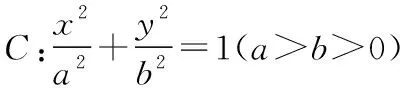
(1)求椭圆C的方程;

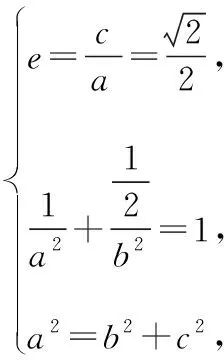

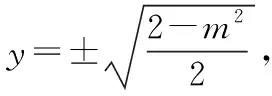


当直线MN的斜率存在时,设直线MN的方程为y=kx+n,
代入椭圆方程化简得(1+2k2)x2+4knx+2n2-2=0,
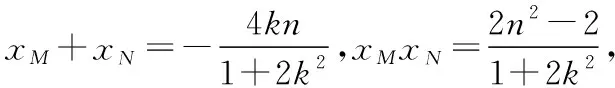
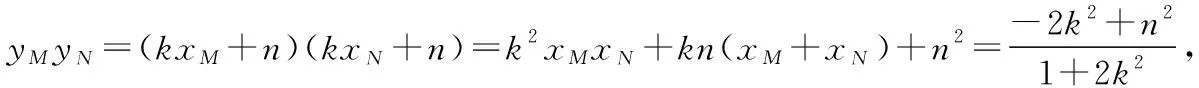

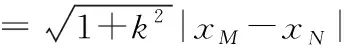


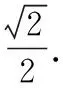
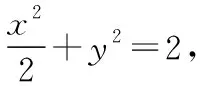




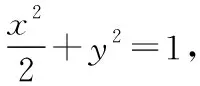

不妨设M(ρ1,θ1),N(ρ2,θ2)(θ1>θ2),

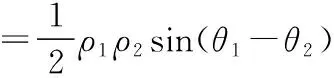
【评析】第二问的“解法一”是本题的一般解法,但运算量较大.“解法二”其关键是联立直线与曲线方程并求交点坐标,巧妙地回避了分类讨论,运算量有所减小.“解法三”是在极坐标系下进行求解,将代数变形问题转化为三角函数恒等变形问题,运算量较小,过程简洁,思路清晰.
二、命题思考
1.对第一问命制的思考
求一个指定的圆锥曲线方程或者求动点的轨迹方程,哪个更有利于解析几何的考查,笔者思考了很久.从表面上看,求轨迹方程没有指定曲线作定向的提示,问题的开放性较大,似乎更能考查求曲线方程,对考生的能力要求也似乎更高.其实不然,因为求指定曲线的方程和求轨迹方程都是考查用代数方法解决几何问题——用曲线方程刻画曲线特征.同时,两种考查方式都在利用等量关系列方程并求出曲线方程,在本质上是一致的.但是求指定曲线方程还可以考查考生从指定曲线中寻找更多的等量关系,兼顾对所指定曲线的特征和性质的考查.因此笔者认为,求指定曲线的方程比求轨迹方程更能全面地考查圆锥曲线.当然,平时考试或训练的命题,两种考查方式都可以考虑.本次命题还要考虑有利于学生的解答,因此决定试题入口要宽,问题由浅入深,层层递进,以提高试题的区分度,最后笔者确定,求一个指定的圆锥曲线方程并选择常见的方法——待定系数法作为本道题第一问的考查方式.这与全国卷的命制思路基本吻合.
2.对第二问命制的思考
圆锥曲线解答题的第二问,一般是已知一条动直线或两条动直线与第一问所求的指定曲线方程的位置关系,根据直线和曲线的性质特征设置有关问题(主要考虑与题目所涉及的圆锥曲线的几何意义、性质特征、方程等),曲线与已知直线所存在的几何关系,以及直线方程等有关的问题.该问的解答主要用代数方法解决几何问题,涉及的内容主要包括平面几何的性质,直线方程,韦达定理,点到直线的距离公式,分类讨论等解析几何的核心内容.本小题的解答主要考查学生的推理论证、运算求解、分析与解决问题等能力,考查化归与转化思想,考查学生直观想象、逻辑推理、数学运算等数学核心素养.

三、答题情况与教学思考
1.答题情况分析
从阅卷情况来看,学生的运算求解能力普遍不高,有一部分学生有思路,但因为运算问题而选择中途放弃.长期以来圆锥曲线解答题在高考中都以中档题或压轴题的形式出现,该题的命制通常是以直线与圆锥曲线相交为背景,通过推理变形后提出有意义的问题.通过对问题的解答考查学生数学运算、逻辑推理等核心素养,考查代数变形、恒等变形等能力和化归与转化思想、函数与方程思想、分类讨论思想、数形结合等数学思想方法.该题的求解对学生的能力要求比较高,考查学生综合运用数学知识解决问题的能力,因此圆锥曲线解答题的求解成为众多学生望而却步的考题,众多非重点中学数学老师欲讲而不敢“逾越半步雷池”,造成“学会放弃也是一种美”的声音颇为流行.不少学生面对圆锥曲线解答题的解答有一定的恐惧心理,甚至直接放弃解答.本次模拟考试阅卷发现有大批量的学生由于各种原因,圆锥曲线解答题位置空白.
2.教学思考
面对当前众多学生的运算求解、推理论证能力普遍不高和面对圆锥曲线解答题有恐惧心理的现状,需要全体教师共同想办法改变这种现状,从而促进学生健康成长.笔者根据多年备考经验,提出几点思考,仅供大家参考.
(1)加强圆锥曲线基础知识的教学.“重构”概念知识,使学生了解圆、椭圆、双曲线、抛物线的定义的形成过程,加强基本量求解和曲线方程求解的训练,掌握曲线的性质特征.逐渐帮助学生梳理知识、构建知识体系,使知识网络化、系统化.日常教学例题和训练题的选取要突出基础性,试题的解答更要讲通性通法、易于归纳总结出解题套路,增强学生学习信心,逐渐消除学生的恐惧心理,有序地提升学生解题能力.
(2)教学设计要科学.教学内容和教学方式方法的选取一定要符合学生的认知和最近发展区,要循序渐进,螺旋上升,逐步提升能力.数学能力综合、复杂,提升数学能力并非一日之功,要循序渐进.建议从以下几方面选取素材开展教学:第一是加强列关于基本量(a,b或c)的方程或其他等量关系式并求解基本量;第二是将已知条件、图形中的几何关系、向量运算转化为代数关系式;第三是根据已知条件求出特定直线方程和指定曲线方程,用代数方法判断直线与曲线的位置关系,若直线与曲线相交则要求交点坐标或弦长,结合曲线上的特殊点求三角形或四边形的面积;第四是根据已知条件求动直线的方程和动点的轨迹方程,判断直线与曲线的位置关系,结合平面向量等其他知识转化列方程并解决相关问题;第五是根据已知两条动直线和某个几何量的等式关系,通过推理得到某两个量的等式关系,列有关弦长或其他几何量关于某变量的方程或函数解析式,并解决相关问题.
(3)重视运算求解能力的培养,注重数学思想方法的教学.从阅卷情况来看,有相当一部分学生有思路,但因为运算问题而选择中途放弃,也有不少学生因为缺乏分类讨论思想导致解答不完整而被扣分,有相当多的学生由于欠缺方程思想、缺乏考虑特殊情形意识而丢掉得分机会等.因此,教师在平时教学时要多选择恰当的素材让学生多尝试列有关方程、解有关方程、求交点坐标、求弦长、求三角形或四边形的面积等培养学生的运算求解能力和方程思想的意识.多结合平面几何知识以及平面向量转化为代数关系式、数形结合分析问题、分类讨论解决问题等,帮助学生理解化归与转化、数形结合、分类讨论等数学思想方法.鼓励学生完整解答圆锥曲线解答题,帮助学生树立解题信心,提高解题能力.
