重视基础、把握本质、领悟思想方法
——2019年全国卷Ⅲ理科第18题评析与备考建议
2020-11-15安徽
安徽 任 静 祝 峰
1.试题呈现
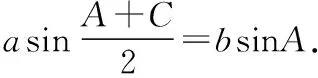
(Ⅰ)求B;
(Ⅱ)若△ABC为锐角三角形,且c=1,求△ABC面积的取值范围.
2.命题分析
试题情境熟悉,条件简单清晰,表达言简意赅,构思巧妙,有效规避“题型”、“套题”.在核心素养导向下,朴实中重“四基”,常规中考“四能”.在三角形问题情境中,着眼于三角变换公式、三角函数的性质、正余弦定理等知识点,考查了学生的逻辑推理、数学运算和直观想象数学核心素养.
3.失分点分析
(1)三角变换出错.三角变换公式是解决三角形问题的基本工具,三角变换出错是低级失误,说明基础知识掌握不牢.

(3)忽视挖掘题目条件.解题过程中应深刻领会题目条件,B=60°,锐角三角形中仅考虑A、B均为锐角不够,还应兼顾A+C=120°,意识不到这一点,C的范围求解就会出错,导致求不准S△ABC的范围.
(4)抽象能力不够.三角形面积有取值范围,则其在变化,变化的原因是什么?能否在函数思想的统领下,辅以几何直观等手段,发现变化的根本原因,抽象出范围问题的求解模型,如“函数模型”、“不等式模型”等,做不到这一点,会导致思维混乱、无路可走、望题兴叹.
4.试题探究
第(Ⅰ)问

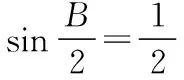
第(Ⅱ)问
角度一:视面积为角的函数


角度二:视面积为边的函数
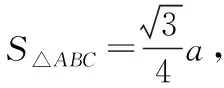
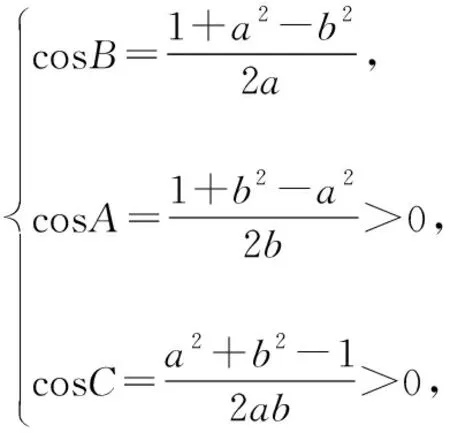
【评析】视三角形形状的不确定性由边a的变化导致,S△ABC是a的一次函数,求出定义域即可求出函数的值域,侧重于余弦定理的应用.
角度三:借助几何直观
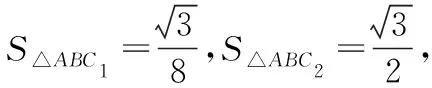

【评析】利用图形描述和分析问题,把复杂抽象的数学问题直观化、形象化,是直观想象素养的体现.论证求解过程需辅以必要的文字和符号说明.
角度四:坐标运算


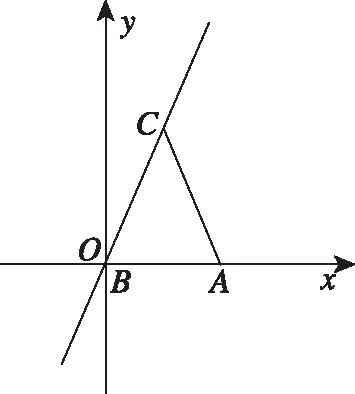
【评析】在平面直角坐标系中,图形的几何特征可以“坐标化”、“方程化”,用方程、不等式的运算解决图形的几何特征,这是解析法的基本思想.
5.试题本源及变式
(1)问题的本源

(2)试题条件设置的变式
∠B=60°表现在边的关系上是a2+c2-b2=ac,能得到这一结论的条件设置方法是多样的,下述表达均具有同样的效果:
(2)acosB+bcosA=2ccosB;
(6)(sinA-sinC)2=sin2B-sinAsinC.
(3)锐角三角形中∠B=60°,c=1,求△ABC面积取值范围的变式
(1)求角C的取值范围;
(2)求角A的取值范围;
(3)求三角形周长的取值范围;
(4)上述问题去掉锐角三角形的条件限制又会怎样?
(4)更广视角
在三角形ABC中,已知∠B=60°,和其中一个邻边c=1,可求S△ABC的取值范围.若保持条件∠B=60°不变,做以下变换,同样可求S△ABC的取值范围.
(1)已知对边:∠B=60°,b=2,求S△ABC的取值范围;
(2)已知对边的中线:∠B=60°,D为AC的中点,BD=1,求S△ABC的取值范围.
6.教学启示及备考建议
(1)规避题型、套题
从这道试题可见,高考试题重视基础知识、基本技能、基本思想、基本活动经验的考查.不能把数学的学习完全定位在考试上,这样会导致教与学都变得很功利,不能只注重“题型”、“套题”的模式化重复训练,而忽视“四基”的落实.高考备考中,解题训练是必要的,但一味追求大量训练,反复总结题型,对各种问题进行“分门别类”,期待考试的时候能对号入座,不顾知识形成和发展过程、忽视问题中数学本质的揭示,舍弃思想方法提炼的做法是低效的.比如正、余弦定理,仅强调它们的结构形式及每个定理能解的三角形类型,不去发掘两定理产生的原因,以及两定理结构形式所对应的思想方法,面对具体问题时学生依然会束手无策.这要求我们在教学中不能只让学生接受现成的结论,只有适时引导学生在具体的问题情境中亲身经历发现问题、提出问题,进而分析和解决问题,才有利于数学学习水平及能力的提高.
(2)注重数学知识之间的联系
数学知识与其他学科知识是联系的,数学学科内部各知识点之间也有着密切的联系,特别是素养导向下的高考数学解答题,基本上会综合考查高中数学中各个分支中不同的知识.高考常在知识点的交汇处命题,本道试题的上述探究过程中,涉及三角变换的基本公式、三角函数性质、正、余弦定理、初中平面几何知识、平面向量、解析几何等相关知识点.因此,在教学中,特别是高三备考复习课中,应阐明高中数学各分支知识点之间的逻辑关系,注重各分支不同数学知识之间的内在关联和逻辑体系,提高学生对高中数学的整体认识,比如函数与方程、不等式的联系;向量工具性在相关问题中的体现等.
(3)把握本质、突出思想
基础知识、基本技能、基本思想、基本活动经验是发展学生数学核心素养的载体,强调“四基”就是要把握数学的本质,在高考备考的教学中,让学生熟练掌握,感悟知识所蕴含的数学基本思想,积累数学思维和实践经验,只有在这个基础上才能促使学生逐步提升数学思维能力,形成和发展核心素养.这就要求教师应设计并实施合理的教学活动,引导学生自己“悟”出数学问题的本质及思想,启发学生主动参与数学学习的各个环节.仅靠死记硬背、机械模仿无法让学生理解问题的本质,更无法让学生感悟数学的基本思想,形成和发展核心素养也就会是无源之水、无本之木,也就无法让学生适应素养导向下的高考试题.
