一道平面向量试题的多种解法及其拓展引申
2020-11-15广东叶土生
广东 叶土生
(作者单位:广东省广州外国语学校)
一、提出问题
在一次我校与其他兄弟学校的联考中,填空题的压轴题是一道向量背景的题目,其题设如下:

本题总体得分率不高,很多的学生是从解三角形的角度研究本问题.向量是高中数学的重要组成部分,其本身自成一知识体系,其既有代数运算,又有几何直观的双重特性,还可以与其他知识(如函数、解析几何、三角函数)相互渗透,从而使得向量的考查形式变得丰富多彩.本文力求从多视角给出本题的解答并给出变式,希望对读者有所帮助.
二、试题的多种解法
以下是笔者在讲评试卷过程中,和学生一起探讨得到的多种解法.

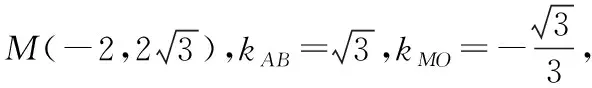
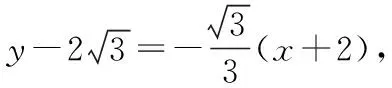

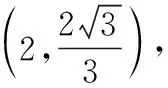
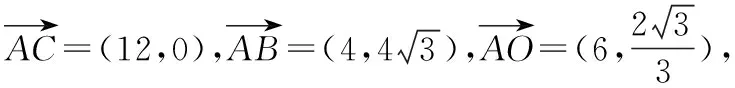
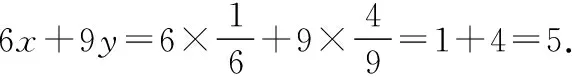

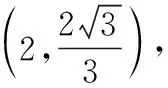
以上解法通过建立平面直角坐标系,即解析法解决此题,思路简单且容易操作,是这一类问题的常见解法.向量有其特有的运算性质,蕴含着丰富的数学思想方法,而一道向量的问题仅仅给出解析法,就显得有点意犹未尽,而且从开发学生数学思维角度考虑,也需要对一个问题从多个角度研究解决方法,在讲评了解析法后笔者又引导学生一起探究其他三种解法.

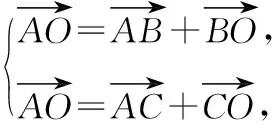



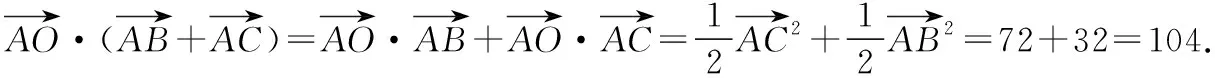

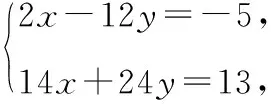
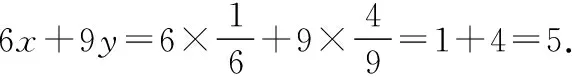


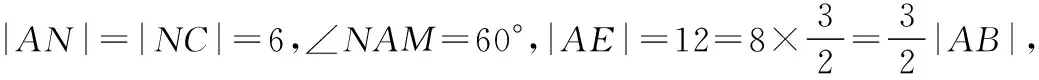



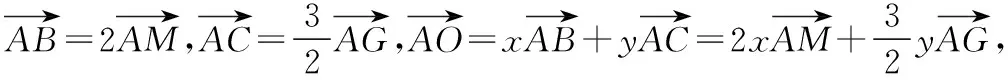
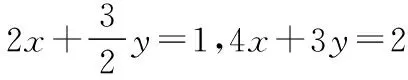


课后,笔者的一位姓潘的学生给出了以下的解法,不妨称为“潘氏解法”.
解法四:(“潘氏解法”)



所以有6x+9y=5.

【评注】“潘氏解法”比以上几种方法都来的自然,并且运算量更小.他充分利用了几何性质,将代数与几何紧密地联系到一起,充分利用几何这一向量的“灵魂”,解法非常漂亮.从潘同学的解法也可以看出他可能得到前面几种解法的提示,也可能独立思考得到结果.这也提醒笔者在后续的教学中要充分利用好每一个“好题”,提升学生的数学思维能力,引导学生敢思考、主动思考、会思考.
三、试题的拓展引申
问题的题设给出了两边和一个夹角,从三角形的角度看,是一个确定性的问题.如果把条件弱化,是否可以有其他考查形式呢?笔者顺着这个想法在后续的课堂给出了两种改编,目的也是为了让学生学会从多个角度看待一个问题,提升学生能力.
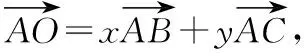
分析:本题将△ABC两边的条件去掉,只给出角A的大小,△ABC是一个不确定图形,需要学生学会转化.本题的解决方法也可以有多种形式,但借用“潘氏解法”思路将会更加自然,以下给出“潘氏解法”思路,其他方法请读者自行思考.
解:如图,设AB=c,AC=b,取AB的中点D,AC的中点E,
则有OD⊥AB,OE⊥AC,所以
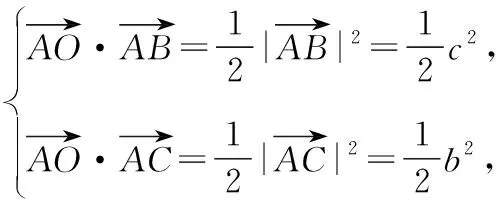




【评注】本题条件中没有给出三角形的边长,但当假设边长后就可以把问题转化为原问题的模型,所以解题思路是一样的,最后利用基本不等式得到最值.



【评注】本题将三角形的条件弱化,从题目的形式看这与前两个问题属于不同类型,但仔细分析发现它们都有很多的共同点,本质是一样的,所以解题方法也类似,最后采用整体代入得到结果.
四、反思
波利亚的数学教育思想中包含这样一个基本观点:数学具有双重性——数学既是演绎科学,又是归纳科学.在新课程的理念中,需要我们通过各种各样的教学方式提高学生的思维能力.探寻“一题多解”是提升学生发散性思维能力的过程,这是一个具有层次性的演绎过程,它在本质上与提升学生归纳思维能力的“通性通法”是相辅相成的,二者也是辩证统一的.新一轮课程改革正如火如荼地推进,对于课堂时效性的要求也越来越高.作为高中数学课堂的一线教师,就必须提高例题的典型性,并引导学生探究、概括一类问题的解法.通过“一题多解”可以开阔学生的思路,避免不假思索地做题.一题多解也是不少数学教师在解题教学时经常进行的一种教学方式,但是一题多解不能只是简单地展示一道习题的多样化解法,这对于提高解题教学效率意义不是很大.我们认为,要努力通过一题多解促进学生深刻理解与考题相关联的不同知识点,这才是一题多解的重要意义所在.
