忽视隐含条件导致错解问题分析

山东 史立霞 秦 振

数学问题中的“隐含条件”，就是指在题目中未明确表达出来，而客观上已存在的条件.“隐含条件”往往隐含在有关概念、性质和知识的内涵中，若明若暗、若隐若现、含而不露，极易被忽视，从而导致解题出错或解答不完整，甚至造成解题困难.因此，分析易错题的类型，找出解题中的错误，研究改正错误的方法，从中吸取教训是我们学好数学，提高数学素养的有效途径.

一、忽视已知条件之间的约束限制

二、未注意条件的隐含作用

【例2】设A，B是一个三角形的两个内角，且tanA，tanB是方程x2+mx+m+1=0的两个实根.求tan(A+B)的值并确定m的取值范围.

【错解】利用根与系数的关系，得

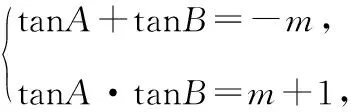
【分析】错因是没有考虑条件A，B是一个三角形的两个内角，对tanA，tanB限制的这个隐含条件.而这个隐含条件影响方程的两个根的范围，因此也影响m的取值范围.

【正解】利用根与系数的关系，得

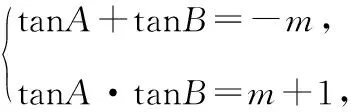
三、未考虑Δ的制约

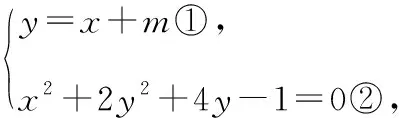
【分析】由于审题不细，没有注意到方程3x2+(4m+4)x+2m2+4m-1=0有实根，即Δ>0这一隐含条件对参数m的限制，使m=y-x中x，y的范围扩大，造成错误.

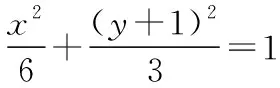
四、忽视定义中的隐含条件

【例4】设等比数列{an}的公比为q，k∈N，k为常数，bn=a(n-1)k+1+a(n-1)k+2+…+ank(n=1，2，3…).试判定数列{bn}是否是等比数列？如果是，求出其公比；如果不是，请说明理由.

【错解】由bn=a(n-1)k+1+a(n-1)k+2+…+ank，bn+1=ank+1+ank+2+…+a(n+1)k，

=qk(常数),所以数列{bn}是等比数列，且公比是qk.

【分析】表面上看没有问题，实际上忽视了等比数列定义中的一个隐蔽性质，即等比数列的任何一项都不能等于零.由上面错解bn=a1q(n-1)k(1+q+…+qk-1)，若1+q+q2+…+qk-1=0，则数列{bn}的各项都为零，显然不是等比数列.请大家注意：“把等比数列依次连续地每k项分成一组，则各组数的和也构成等比数列”是不正确的.

【正解】由错解，当1+q+q2+…+qk-1≠0，即q≠-1与k是偶数不同时成立时，数列{bn}是等比数列，公比为qk.

当1+q+q2+…+qk-1=0，即q=1且k是偶数时，数列{bn}是各项都为零的常数列，它不是等比数列.

五、未注意变量间的制约作用

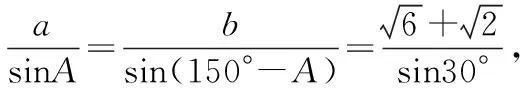
六、未注意函数定义域的限制

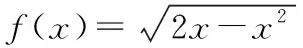
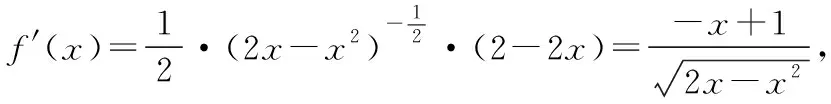
【分析】错因是审题不细，没有考虑隐含条件函数的定义域对函数的制约作用，导致错误.

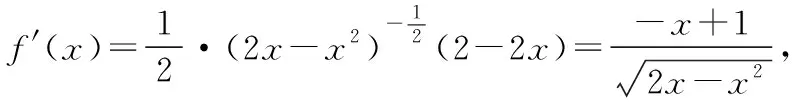
七、忽视两个变量之间的区别与联系(倾斜角与斜率)

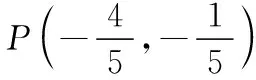
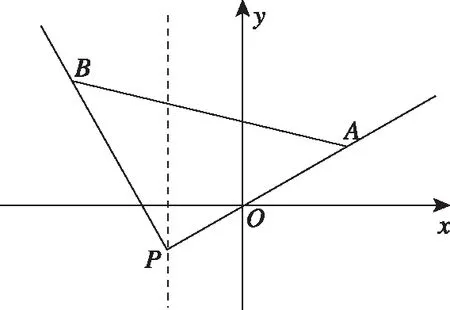
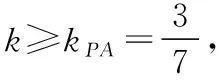
八、未注意方程的“常数”中隐含的条件

( )

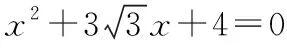
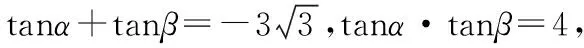
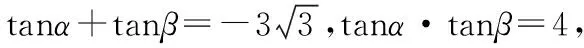
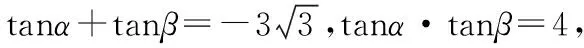
九、未注意定理成立的隐含条件

【例9】若函数y=f(x)与y=g(x)是[a,b]上的两条光滑曲线，且两条曲线在[a,b]上不相交，则这两条曲线及直线x=a，x=b所围成的平面区域的面积为

( )

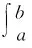
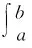
【错解】由定积分的定义及几何意义可知，D正确.

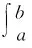
十、未注意公式成立的隐含条件

【例10】已知数列{an}是一个公差大于0的等差数列，且满足a3a6=55，a2+a7=16.

(1)求数列{an}的通项公式；

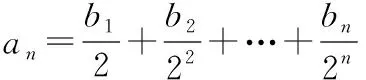
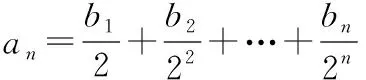
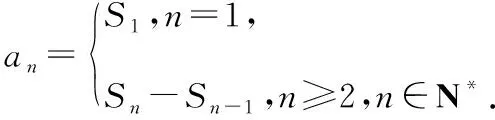
【正解】(1)略.

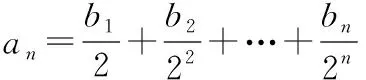
十一、忽视实际应用问题隐含的条件

【例11】要将大小不同的甲、乙两种木板截成A，B，C三种不同规格的木板，每种木板可同时截得三种规格的木板的块数如下表：

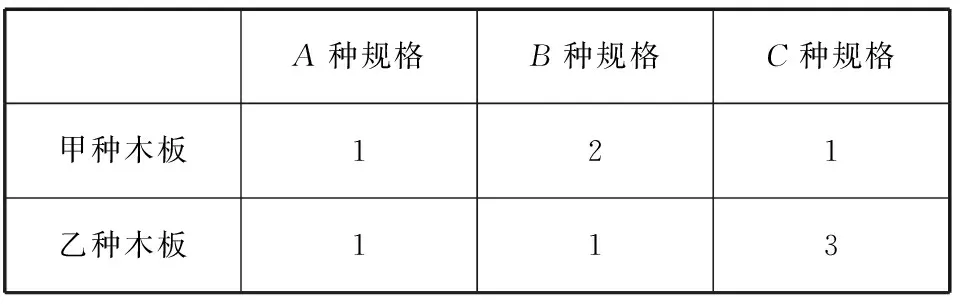
A种规格B种规格C种规格甲种木板121乙种木板113

每种木板的面积，甲1 m2，乙2 m2.现在需要A，B，C三种不同规格的木板12，15，27块，问在满足需要的情况下，使用的甲、乙两种木板面积和最小值为多少？

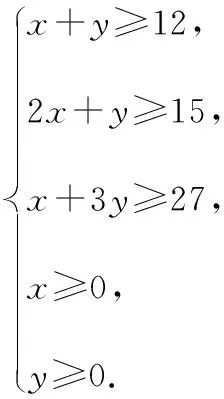
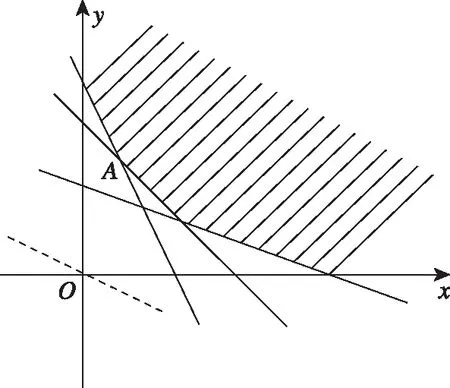
【分析】错因是没有考虑实际问题中的隐含条件：木板的需要量是一个正整数，而导致错误.

在解题过程中，若能及时发现和运用隐含条件，不仅可以迅速找到解题的突破口，使解题过程简单、清晰，还可以促进我们对各种基础知识的融会贯通，逐步培养全面分析问题和解决问题的能力，这也是实施素质教育,提高学生数学素质的重要举措.