探究函数最值问题求解之思维痛点
2020-11-15浙江余继光
浙江 余继光
诊断函数最值问题中的思维痛点症状——定义域变动引起思维之痛、复合结构引起思维之痛和分类标准难定引起思维之痛等.探究其产生的根源——代数式结构的转化能力不强、求函数最值的基本方法不熟和综合结构分解的基本思想不牢.给出解除痛点的方法——识类型找准方法、定标准科学分类和善转化变形到位.通过积累解除痛点的经验,提升函数最值问题求解的成功率.
函数的最值问题依赖于函数的定义域与对应法则,一旦涉及参数,变动的定义域与复杂的对应法则导致函数的最值求解时产生思维痛点,而函数的最值问题在高考数学命题中永不消逝.
一、思维痛点的主要症状
1.定义域变动引起的思维之痛

现象:忽略函数定义域而导致出错.


解读:
(1)此题重点不是数列概念而是函数概念,特别是函数的定义域意识,许多学生忽略了函数定义域而导致出错;
2.复合结构引起的思维之痛
问题2:函数f(x)=-x2+3x+a,g(x)=2x-x2,若f(g(x))≥0对∀x∈[0,1]恒成立,则a的取值范围是________.
现象:复合函数结构转化后,不等式恒成立转化不到位.
分析:a≥g2(x)-3g(x),对∀x∈[0,1]恒成立,
设F(x)=y2(x)-3g(x),则上式转化为
求F(x)=g2(x)-3g(x),x∈[0,1]时最大值,
g′(x)=2xln2-2x,x∈[0,1],
因为g′(0)>0,g′(1)<0,所以∃x0∈[0,1],使g′(x0)=0,
所以g(x)∈[1,g(x0)],所以F(x)在[1,g(x0)]上单调递减.
所以F(x)max=F(1)=-2,所以a≥-2.
解读:
(1)根据函数的复合结构转化为一个不等式恒成立问题,然后变参分离转化为二次函数结构的最值问题,定义域的判断是解题的关键;
(2)在函数最值研究中,定义域意识非常重要,因为根据函数的三要素,函数的值域或最值依赖于函数的定义域与对应法则,虽然此问题的对应法则为复合结构,但内外层函数均为具体函数,不构成难点,而函数定义域明确给出限制,必须考虑由于定义域限制而导致函数g(x)值域的限制,从而导致F(x)定义域的变化.
3.分类标准引起的思维之痛

现象:如何分类建立|AB|的函数没有思路.
分析:当x>0时,
(1)当a>4时,直线y=4与函数f(x)的图象没有交点;
(2)当a=4或a=0时,直线y=4与函数f(x)的图象只有一个交点;
(3)当0 所以g(a)=|xA-xB|=4,故g(a)的最大值为4. 解读: (1)从函数结构上看,f(x)与对勾函数相关,但由于含参函数的本质发生了变化,能从结构上看出,当a<0时,f(x)就不是对勾函数了; (2)此函数含有绝对值与参数,都是引起分类讨论的刺激信号,分类标准的确定是一个难点,此处抓住“直线y=4与函数f(x)的图象交点个数”进行分类,看准问题的关键点; (3)此题g(a)的最大值并不完全是找到此函数后再求最值,而是根据g(a)的几何意义,在分类讨论中确定. 问题4:N是等腰直角△ABC所在平面上一点,且点N与点A分别位于直线BC的两侧,如图,若BN=4,CN=2,求四边形ABNC面积的最大值. 现象:选择变量建立关于面积的函数时思维受阻,建立关于面积的函数后,面对无理函数,如何求其最值思维也受阻. 分析:在△ABC中,设BC=a,AC=b,则a2=2b2,为了建立关于△BCN面积的函数,需要: =5+4(sinθ—cosθ)(变换化简函数) 解读: (1)此题第一步是建立面积函数模型,要选择变量,因为△ABC是等腰直角三角形,边之间有数量关系a2=2b2,而△BCN已知两边,必须找到夹角与此变量间的关系,于是用到余弦定理; 问题5:已知函数f(x)对任意实数x均有f(x)=kf(x+2),其中常数k为负数,且f(x)在区间[0,2]上有表达式f(x)=x(x-2). (Ⅰ)求k的值并判断f(x)的周期性; (Ⅱ)写出f(x)在[-3,3]上的表达式,并讨论函数f(x)在[-3,3]上的单调性; (Ⅲ)求出f(x)在[-3,3]上的最小值与最大值. 现象:如何确定k的值思维受阻,对函数周期性的分析思维受阻. 分析:(Ⅰ)因为f(x)=kf(x+2),所以f(x+2)=kf(x+4),所以f(x)=k2f(x+4), 所以k2=1,又k<0,所以k=-1,所以f(x)=-f(x+2)=-[-f(x+4)]=f(x+4), 从而函数f(x)是周期为4的周期函数. 所以f(x)在[-3,3]上的单调增区间为[-3,-1],[1,3],单调减区间为[-1,1]; (Ⅲ)f(x)在[-3,3]上的最小值为-1,此时x=-3或x=1;最大值为1,此时x=-1或x=3. 解读: (1)此题确定k值的思维方法是难点,很重要也非常经典,值得学生学习借鉴; (2)由k值的确定,然后判断函数的周期性是常规思路; (3)当函数解析式与单调性都比较明确后,确定函数的最值就显得简单多了. 现象:分类出错,讨论不到位,二次函数最值与对称轴之间关系把握不到位. 解读: (1)此题为文科高考数学题,对二次含参函数求最值是一个经典思维过程,抓住二次函数对称轴进行分类是一个基本的思路; (2)通过函数图象的分类表示,学生可以较清晰的理解“抛物线弧”的分类与最值的关系; (3)一个动抛物线在定区间上的最值,一般是一个分段函数,最后结论表达要规范完整. 函数对应法则的信息中,代数式是基本的,因此代数式结构特征的判断或转化成为函数最值的“第一杀手”,然而,学生由于代数式结构转化能力不强导致求解失败或受阻. 求函数最值问题的基本方法很多,不同类型的函数要用不同的方法处理,由于学生掌握的函数最值的求解基本方法不足或运用不熟,从而找不到问题求解的基本思路. 解决函数最值问题的基本思想方法——判断函数最值的类型+转化技巧+变形能力+分类和运算能力,是问题突破的基本途径.没有在脑海中建立起这些基本思想方法,就无法解决此类问题,痛点自然产生. 函数最值问题的类型比较多,每一个类型都有其特点,解决此类最值相应的方法要熟悉,不能用错.比如,判别式法求某一类二次函数的最值时,使用限制条件很关键,否则就要出错. 解法1:判别式法 首先,y≠1,y(x2-x+1)=x2-x+3, 即(y-1)x2-(y-1)x+y-3=0, Δ=(y-1)2-4(y-1)(y-3)≥0,(y-1)(-3y+11)≥0. 解法2:对勾函数单调法 u+1≥1,1 问题3中分类标准的确定是一种智慧,在一个综合数学题中,把握问题中的矛盾点是分类标准制定的基石.众所周知,三个数比较大小判断谁最大,两两比较后确定或寻找“桥”当媒介来比较,然后确定谁最大. 复杂结构函数的最值,一般都要进行一些转化,转化的目的就是归类,类型找准了,方法使用对了,函数的最值探求就解决了一半. 解法2简洁,但配方过程技巧太高,这种配方技巧并非普通学生通过个人努力即可掌握,学生看到这样的解答可能会有挫败感:是不是我能力不够(不会配方),不能解这个问题呢?一个好的问题和解答,是可以帮助人改善自我的,是可以增加学生学习的乐趣和信心的. 通过把条件作一系列等价转化,原问题被转化为一个容易解决的熟悉问题,这时几乎不需什么技巧和计算,就可以得到原问题的解答. 善于不断积累函数最值的各种分析方法,多角度变形,挖掘其特征,特别是各类可能情形的全面考虑,意在培养全面思考问题的素养,而不仅是线性思考某一个问题;对于函数最值问题,学会分解到基础知识与基本方法层面,然后逐一解决,这也是在培养面对复杂问题时,认识问题本质,化整为零,个个击破的素养. 及时解除解决有关函数最值问题中遇到的思维痛点,一方面积极地面对函数结构变形中的痛点,分析原因,找到产生痛点的根源;另一方面寻找解除痛点的思路与方法,这一过程本身也是积累在这一领域的求解经验,从而驾驭此类问题的求解.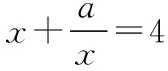

4.无理函数引起的思维之痛






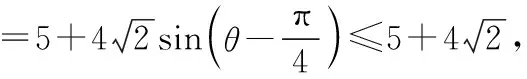
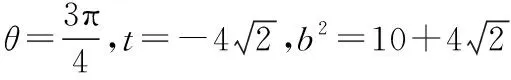

5.周期函数引起的思维之痛



6.含参函数引起的思维之痛









二、思维痛点的产生之源
1.代数式结构的转化能力不强
2.求函数最值的基本方法不熟
3.综合结构分解的基本思想不牢
三、思维痛点的解除之法
1.识类型找准方法


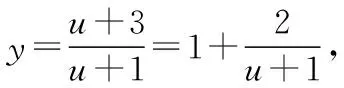

2.定标准科学分类
3.善转化变形到位






四、解除思维痛点积累经验之旅
1.善于积累思维方法
2.及时解除思维痛点
3.勤于总结思维经历

