突破圆锥曲线运算关的训练策略

浙江 朱旭颖

在一轮复习中，从圆锥曲线题的运算障碍看，圆锥曲线复习的关键点：一要突破运算心理障碍关；二要突破运算方法优化关；三要突破运算方向有序关.通过简化训练、转化训练和优化训练提升圆锥曲线复习的有效性.

每年高考数学应试中，学生得分较少且头痛的题目之一就是圆锥曲线相关的问题——用代数方法解决几何问题的重点对象，普遍认为圆锥曲线问题运算量大，学生运算能力不足，在高考数学有关圆锥曲线的复习中，运算关是复习突破的第一要务，现以近几年高考数学圆锥曲线题为例来探究运算关的突破策略.

一、圆锥曲线问题的运算障碍

圆锥曲线求解过程中不可避免地涉及方程与不等式的求解，运算次序不同，结构识别不对，就会导致运算障碍；圆锥曲线问题中涉及的变量较多，消元顺序不同，也会导致运算繁杂程度不同，错点、漏洞和智慧点缺失构成运算障碍关.

1.解方程(不等式)的痛点

学生在解方程运算、解不等式运算、代数变形运算和数字运算中简化能力的不足可能形成痛点，不能越过圆锥曲线的运算障碍关.

【例1】(2019·全国卷Ⅰ理·10)已知椭圆C的焦点为F1(-1,0)，F2(1,0)，过F2的直线与C交于A，B两点.若|AF2|=2|F2B|，|AB|=|BF1|，则C的方程为

( )

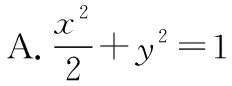
【解析】如图，设|AF2|=2|F2B|=2r1，|AF1|=r2.

解得a2=3，b2=2，故选B.

【体验反思】(1)充分利用智慧点——利用同一个角在不同三角形中运用余弦定理，建立方程；

(2)掌握技术点——列方程解方程技术，数值运算技术.

【变式】(2018·全国卷Ⅲ理·16)已知点M(-1，1)和抛物线C：y2=4x，过C的焦点且斜率为k的直线与C交于A，B两点.若∠AMB=90°，则k=________.

【体验反思】此题在解方程等代数变形中，只要出现一点失误(写错一个负号或数字)都会导致结果错误，比如(*)处，在不同消元思想支配下，运算方向不同，就会导致运算结果表现形式不同，稍微有一点失误，再利用韦达定理时，结果就不对，后续运算不可能正确.

2.圆锥曲线运算的智慧点

【体验反思】(1)圆锥曲线问题中出现共线向量时，智慧点就是点的坐标之间的沟通，如果不能掌握这一点，不仅运算量大，而且容易出错；

(2)圆锥曲线问题中的方程(组)的特点就是变量多，消元时方法多，运算智慧点多，但总的原则是遵循运算的顺序，关注代数式的结构；

(3)解方程组时，一般会有多种运算途径，一要根据代数结构的特点来决定运算方向，确定求解方法；二要遵循一些规则，如先化无理式为有理式，化分式为整式，化分数为整数，有公约数(式)先约分.总之，注意寻找最优的求解方法.

【素养水平】《普通高中数学课程标准(2017年版)》中对综合问题情境中的运算有着明确的水平要求，解此问题的过程中需要的数学运算水平：在综合的情境中，能够把问题转化为运算问题，确定运算对象和运算法则，明确运算方向.能够对运算问题，构造运算程序，解决问题.能够用程序思想理解与表达问题.

二、圆锥曲线运算训练方向

1.突破解方程(不等式)的心理障碍

【体验反思】这是2016年浙江高考数学圆锥曲线题解析中的节选，专家多次强调要在圆锥曲线问题中检测考生的运算能力，其中解方程与解不等式是主旋律，上述的每一步都是学生在数学学习中必须掌握的内容，但在综合运算时，由于运算方向不明确，变形能力弱而导致止步不前，丢失大分.

【素养水平】《普通高中数学课程标准(2017年版)》中对关联的情境中的运算有着明确的水平要求，解此问题的过程中需要的数学运算水平：能够在关联的情境中确定运算对象，提出运算问题.能够针对运算问题，合理选择运算方法、设计运算程序，解决问题.能够理解运算是一种演绎推理.能够在综合运用运算方法解决问题的过程中，体会程序思想的意义和作用.

2.突破圆锥曲线运算技术障碍

圆锥曲线题中运算量较大，其中涉及运算技术的比重较大，学生面对复杂的代数式只会硬算，缺少对代数结构的分析与识别，因此选择适合的运算途径尤为重要.

【例4】(2019·浙江卷·21)如图，已知点F(1，0)为抛物线y2=2px(p>0)的焦点.过点F的直线交抛物线于A，B两点，点C在抛物线上，使得△ABC的重心G在x轴上，直线AC交x轴于点Q，且Q在点F的右侧.记△AFG,△CQG的面积分别为S1,S2.

(Ⅰ)求p的值及抛物线的准线方程；

所以抛物线的准线方程为x=-1.

(Ⅱ)设A(xA,yA),B(xB,yB),C(xC,yC)，重心G(xG,yG).令yA=2t,t≠0，则xA=t2.

所以直线AC的方程为y-2t=2t(x-t2)，得Q(t2-1,0).

由于Q在焦点F的右侧，故t2>2.

令m=t2-2，则m>0，

【体验反思】(1)建立面积之比的函数是第一关，大多数考生可以达到，但是面对复杂的繁分运算时，纷纷下马，事实上，按照分式运算规则，通分，除以一个代数式就是乘以这个代数式的倒数；

(3)运算中最重要的是要观察结构、随步化简.

3.强化运算方法优化训练

圆锥曲线中的点与线是主体，代数化过程中必然涉及表达方式，设得巧，运算就简化，否则就繁杂，无法进行下去.

【体验反思】(1)充分利用智慧点——挖掘平面几何性质，运用焦半径性质；

(2)熟练掌握技术点——建立圆的方程技术，解方程技术.

【变式】(2018·浙江卷·21)如图，已知点P是y轴左侧(不含y轴)一点，抛物线C：y2=4x上存在不同的两点A，B满足PA，PB的中点均在C上.

(Ⅰ)设AB中点为M，证明：PM垂直于y轴；

所以y1+y2=2y0,

因此，PM垂直于y轴.

(2)题中第(Ⅱ)问涉及三角形面积的表达方式，因此面积函数的繁杂程度也不同；

因此结合这几点，复习教学中有意识地设置“问题思考点”，对于训练学生的运算思维很有用处.

4.关注运算方向的转化训练

圆锥曲线的几何性质要通过代数运算来证明或求解，其中合理转化是关键.比如，证明互补的两个角的关系，利用正切函数性质转化为斜率之和为0，这是此类问题最常见的转化模式.

(Ⅰ)当l与x轴垂直时，求直线AM的方程；

(Ⅱ)设O为坐标原点，证明：∠OMA=∠OMB.

【解析】(Ⅰ)由已知得F(1,0)，l的方程为x=1.

(Ⅱ)当l与x轴重合时，∠OMA=∠OMB=0°.

当l与x轴垂直时，OM为AB的垂直平分线，所以∠OMA=∠OMB.

当l与x轴不重合也不垂直时，设l的方程为y=k(x-1)(k≠0)，A(x1,y1),B(x2,y2)，

由y1=kx1-k,y2=kx2-k得

从而kMA+kMB=0，故直线MA与MB的倾斜角互补，所以∠OMA=∠OMB.

综上，∠OMA=∠OMB.

【体验反思】(1)题中第(Ⅰ)问是简单的，每个学生都可以做好，第(Ⅱ)问，证明两个角相等，画出图形后，除了要考虑特殊位置关系外，还要考虑如何通过代数方法来证明两个几何角相等，引导学生关注两个角之间的联系——倾斜角互补性，利用两直线斜率互为相反数可以解决；

(2)第(Ⅱ)问中如何验证两直线斜率互为相反数，必须寻找一个“桥”——直线l的斜率，此时将几何问题转化为代数问题已经成功，剩下的就是运算了；

因此，由上述几点可见，运算的本质是表达与转化——表达的简洁性，转化的合理性.

三、圆锥曲线运算关突破策略

1.观察结构，同步化简

圆锥曲线运算中不论是方程求解还是代数式变形，面对复杂的代数式，第一，从结构上入手，有公因式首先要提出来或约去；第二，无理式化有理式，分式化整式，多元化一元都是必须坚持的优先原则；第三，不断地观察所面对的复杂代数式中的特点，以便明确下一步的运算方向.

(1)解方程运算中，始终观察方程的特点，充分利用方程给出的信息，减少运算步骤；

(2)熟练掌握运算技术，时刻关注运算方向并灵活运算.

2.研究途径，寻找方向

圆锥曲线中的运算问题大多都需要合理转化后才能解决，转化方向很多，运算途径也很多，引导学生总结规律，积累转化类型与转化方法，每年高考圆锥曲线问题都在此处设置障碍，通过训练一旦突破，圆锥曲线问题便可迎刃而解.

3.强化意识，提运算力