中心概念及其在规则提取中的应用*
2020-11-15闫心怡陈泽华
温 馨,闫心怡,陈泽华+
1.太原理工大学 大数据学院,太原 030024
2.太原理工大学 电气与动力工程学院,太原 030024
1 引言
规则提取是数据挖掘的研究热点。粗糙集理论[1]与概念格理论[2]是数据处理与知识发现[3-6]的重要工具。近年来,众多学者致力于两种理论的研究并提出了不少决策规则提取算法[7-15],文献[7]将决策信息系统分层粒化,在不同的粒度空间下求取粒关系矩阵,并从中获取启发式信息去除冗余属性,设定终止条件实现决策规则的挖掘,但当冗余属性较多或者样本集较大时,规则约简难度增加;文献[8]提出了一种从决策形式背景生成概念,进而推导无冗余规则的算法,该算法在一定程度上降低了算法复杂度,在某些情况下,获取的决策规则仍然存在冗余属性;文献[11]主要研究决策形式背景的规则获取和属性约简问题,基于面向对象概念和面向属性概念,提出了面向对象决策规则和面向属性决策规则的概念,并利用条件概念格与决策概念格外延集合的等价类关系进行决策规则提取;文献[13]为解决传统的决策规则只能判断对象是否具有某种决策属性,以及无法准确判断决策知识的内在性质的问题,提出含有多个决策属性且决策属性取值为多值的序决策形式背景及其序决策概念格,并实现了基于规则不变的属性约简;文献[14]利用正向尺化与反向尺化实现信息系统与形式背景之间的相互转化,定义了多粒度标记形式背景,并实现了多粒度标记决策形式背景的规则提取;文献[15]提出介粒度标记形式背景的概念,之后基于此,给出多粒度标记决策形式背景的介粒度知识发现方法,得到粗细介粒度标记形式背景之间的决策蕴涵诱导关系。
本文针对决策信息系统,基于形式概念分析理论,将决策信息系统通过转化为决策形式背景进行决策规则提取,并提出一种基于中心概念的最简规则提取算法,该方法的提出将概念生成的过程与规则提取进行有效融合。不必生成所有概念,即决策规则提取完毕时概念生成过程也将结束。该算法避免了传统基于决策形式背景的决策规则提取算法[7,10-11]需要同时生成条件形式概念及决策形式概念的计算复杂性。决策规则的提取是本文研究的重点,而概念的生成仅是一个条件,没有绝对必要将所有概念全部生成。理论分析和实验证明体现出本文方法的有效性。
2 预备知识
定义1[1](决策信息系统)设DIS={U,C⋃D,V,f}是信息系统,其中U为对象集,C为条件属性,D为决策属性,用V表示属性集C⋃D的值域;f:U×(C⋃D)→V是信息函数,它指定U中每个对象的属性值。若C⋂D=∅,则称该信息系统为决策信息系统,也称为决策表。
定义2[1](等价类)在决策信息系统DIS中,∀B⊆(C⋃D),定义等价关系ind(B)={(x,y)∈U×U|∀b∈B,f(x,b)=f(y,b)},其中ind(B) 为属性子集B导出的划分,而产生的等价类记作[x]ind(B)或[x]B。
定义3[2](形式背景)形式背景可以用一个三元组T=(U,A,I)来表示,其中U表示非空有限对象集,称为论域;A表示非空有限属性集;I满足I⊆U×A,表示形式背景的一种二元关系,(u,a)∈I(其中u∈U,a∈A)表示对象u拥有属性a,否则(u,a)∉I表示u没有属性a。在形式背景T=(U,A,I)中,令2U、2A分别为对象集U和属性集A的幂集,对于任意对象集合X(X⊆U)和任意属性集合B(B⊆A),Wille 定义了两个映射X↑:2U→2A和B↓:2A→2U[2]:

定义4[2](形式概念)三元组T=(U,A,I)为一个形式背景,令X⊆U,B⊆A,若X↑=B且B↓=X,则称二元组(X,B)为一个形式概念,其中X被称为这个概念的外延,B被称为这个概念的内涵。为方便叙述,可将形式背景T下的所有概念存入L(T)中。记L(T)中的两个概念为(X1,B1)、(X2,B2),若满足条件X1⊆X2(或B2⊆B1)时,则称概念(X1,B1) 是(X2,B2) 的子概念,概念(X2,B2)是(X1,B1)的父概念。可定义L(T)中的任意两个概念间的逻辑运算:

为了便于理解上述逻辑运算过程,下面将通过具体实例(例1)来详细说明:
例1如表1 所示,形式背景T=(U,A,I),其中U={x1,x2,x3,x4},A={a1,a2,a3,a4}。
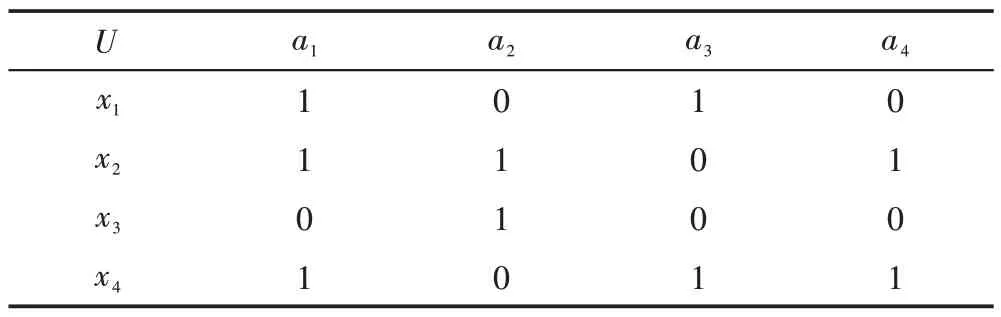
Table 1 Formal context表1 形式背景
其中概念(124,a1)与(14,a1a3)为表1 所示的形式背景中可求得的两个概念。
针对式(3)而言有:
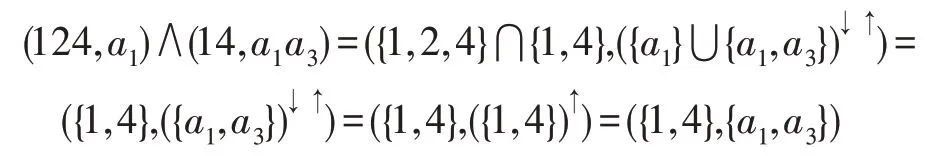
针对式(4)而言有:
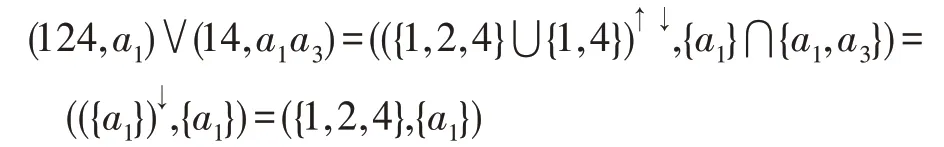
定义5[8](决策形式背景)五元组S=(U,A,I,D,J)为一个决策形式背景,其中(U,A,I)和(U,D,J)为形式背景,U为对象集,A为条件属性集,D为决策属性集。
定义6[16](协调决策表)在决策信息系统DIS中,如果ind(C)⊆ind(D),则称S为协调决策表,否则称为不协调决策表。本文讨论的是协调决策表。
3 中心概念与决策规则
3.1 概念定义
中心概念是本文提出的定义,也是本文的核心内容,本文所做的工作都将围绕中心概念展开。中心概念同时考虑了条件属性与决策属性之间知识的关联性,且具有丰富的知识内涵。
定义7(外延)任一决策信息系统S可转化成决策形式背景T=(U,A,I,D,J),记Z=A⋃D,对于∀Z′⊆Z,有以下关系:

定义8(综合概念)在一个决策形式背景S=(U,A,I,D,J)中,对于一个概念(X,B),其中X⊆U,B=C⋃d(C⊆A,d∈D) 且满足C≠∅,d≠∅,同时X↑=B,B↓=X,此时称(X,B)为综合概念。
定义9(中心概念)对于一个综合概念(X,B),其中B=C⋃d且满足C↓⊆d↓,此时称(X,B)为一个中心概念,中心概念包含了综合概念中最简单的逻辑关系,直接蕴含了决策信息系统中的规则信息。
定理1在决策形式背景S=(U,A,I,D,J)中(X,B)为一个中心概念,若∃(X,B)∈L(T),此时可以确定一条决策规则记C→d。对于决策规则C→d,C={c1,c2,…,cn},若∃ck∈{c1,c2,…,cn}s.t.{C-ck}↓⊆X,则称决策规则C→d中存在冗余属性ck。
定理2若(X,B)为一个中心概念,其中B=C⋃d,C={c1,c2,…,cn}且有决策规则C→d,∀ci∈C,c′={c-ci},如果满足c′↓⊄X,则称决策规则C→d为最简决策规则。
证明反证法。若∀ci∈C,c′={c-ci},如果满足c′↓⊄X,C→d不是最简决策规则,则∃cj∈C={c1,c2,…,cn}使得{C-cj}↓⊆X,显然与前提相矛盾,故C→d为最简规则。
3.2 中心概念与传统概念
本文针对决策信息系统规则抽取的问题提出了一种新的概念——中心概念,中心概念是概念,但内涵更加丰富。内涵中不仅包含决策信息系统中的条件属性C,也包含了决策属性d,同时这两种属性之间存在一种逻辑关系即C↓⊆d↓,而这种关系成为进行规则提取的充要条件。故一个中心概念不单满足概念定义,且其内涵中内部属性之间体现了决策规则。
4 基于中心概念的最简规则提取算法
4.1 算法描述
中心概念体现出条件属性与决策属性之间的蕴含关系,本文提出了基于中心概念的决策信息系统最简规则提取算法(记作算法1),其具体算法流程描述如下所示:
算法1基于中心概念的最简规则提取算法
输入:决策信息系统DIS=(U,C⋃D,V,f)。
输出:最简决策规则。
步骤1对完备决策表DIS进行预处理,将其转换成决策形式背景S=(U,A,I,D,J),记Z=A⋃d。
步骤2初始化n=1,Rules=∅,Concept=∅,Exten=∅,Del=∅。//Exten为外延集合,Del为被剔除概念的集合
步骤3对于z∈Z,计算n=1 次的形式概念(z↓,z↓↑),并将第一次求得的概念存入Concept。
步骤4依次判断第n层时的概念(X,B),若C⊂B,d∈B,C↓⊆d↓且X⊄Exten,则Rules=Rules⋃{C→d},Exten=Exten⋃X,同时对提取完规则的概念(X,B)进行标记并存入Del中。
步骤5对概念集Concept进行更新:Concept=Concept-Del。
步骤6判断Exten是否等于U:若相等,则转至步骤9;否则,转至步骤7。
步骤7此时n=n+1,对当前Concept中的所有概念按照式(3)进行两两相交逻辑运算,并记录新产生的概念。
步骤8将新产生的概念重复步骤4~6,若Exten与U相等,则转至步骤9;否则,转至步骤7。
步骤9输出Rules中的最简决策规则。
算法1 主要分为两部分:第一步将输入的决策信息系统转化成决策形式背景,决策属性也参与第一层形式概念的生成,根据定义9 选择满足条件的中心概念,并由定理1 进行决策规则的提取;第二步判断Exten中的元素是否覆盖整个论域,若没有覆盖,则在下一层概念生成之前将前一层的中心概念剔除,剩余概念集作为基概念再参与下一层的生成运算,然后重复第一步中的规则提取过程,否则重复第二步继续提取规则,直到Exten中的元素覆盖整个论域。
4.2 算法复杂度分析
在完备决策信息系统DIS=(U,C⋃D,V,f) 中将DIS转化成决策形式背景S=(U,A,I,D,J),对于∀u∈U,∀p∈A⋃D在决策形式背景S中满足(u,p)∈I的属性值共有|U||A+D|个。求概念每一层的时间复杂度的基数为O(|U|2|A+D|2),共有lb(|U||A+D|)层。假设算法共产生N条决策规则即N个中心概念,而该算法生成概念的过程中要剔除提取完规则的中心概念,其复杂度为O(N-1)。并且如果Exten已经覆盖整个论域,算法执行完毕,但实际上有可能并没有将所有的概念全部生成出来。故整个算法的复杂度要小于等于O(|U||A+D|)+O(|U|2|A+D|2lb(|U||A+D|))+O(N-1)。
5 实验分析
5.1 实例说明
下面通过实例来详细说明算法1 的执行流程。
例2决策信息系统DIS=(U,C⋃D,V,f),其中论域U={x1,x2,…,x8},条件属性集C={a,b,c},决策属性集D={d}。如表2 所示。
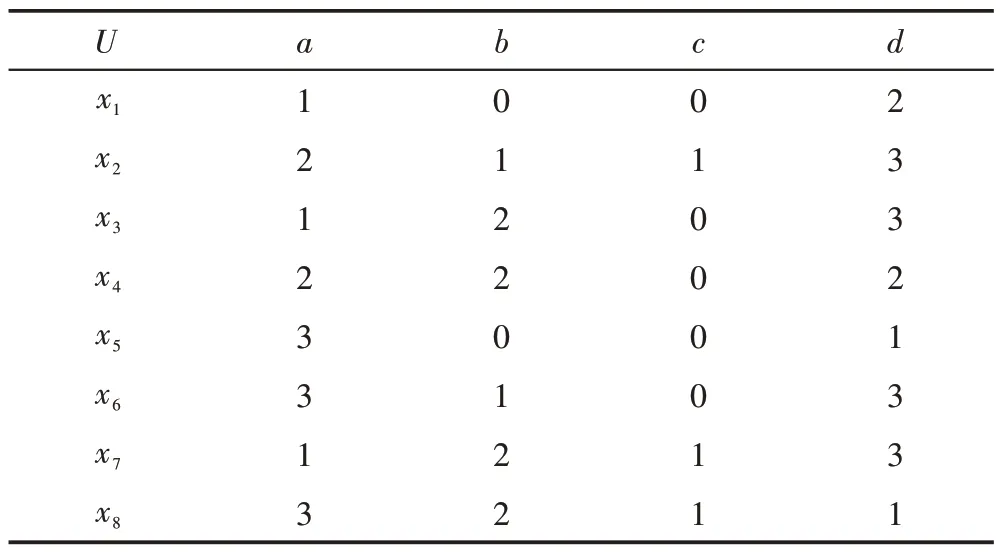
Table 2 Decision information system表2 决策信息系统
将表2 的决策信息系统转化为决策形式背景S=(U,A,I,D,J),如表3 所示。
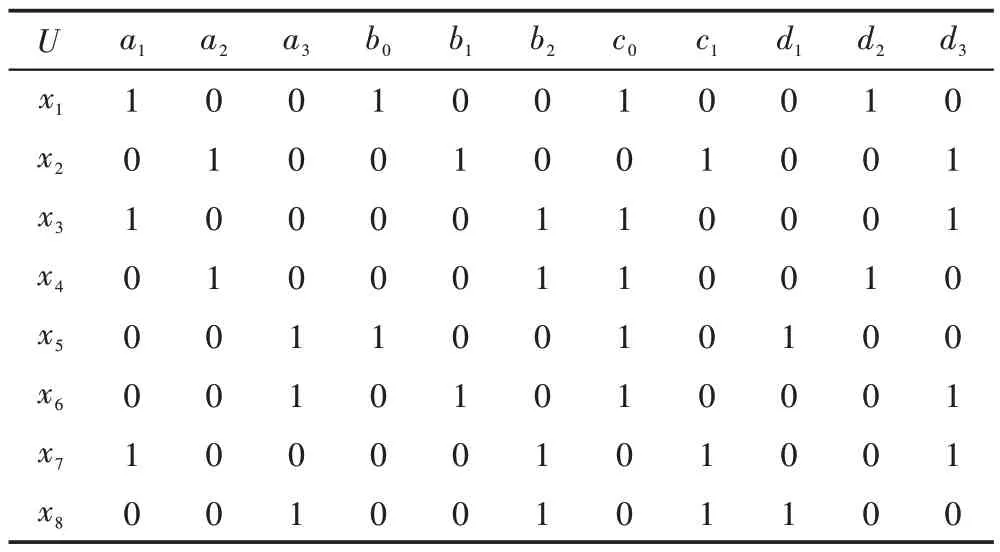
Table 3 Decision formal context表3 决策形式背景
对于∀z∈Z,由(z↓,z↓↑)可求取第一层概念(其中外延元素简写为数字,例如概念(x1x3x7,a1) 简写为(137,a1)):(137,a1),(24,a2),(568,a3),(15,b0c0),(3478,b2),(26,b1d3),(278,c1),(13456,c0),(58,a3d1),(14,c0d2),(2367,d3)。从第一层概念中选取满足定义9 的中心概念并进行规则提取,如表4 所示,其中(26,b1d3)满足条件,此时可进行决策规则提取,此时Exten中的元素为{2,6},没有覆盖整个论域元素,因此需计算下一层概念。

Table 4 Rule list of the first layer of central concept表4 第一层中心概念的规则列表
生成第二层概念时,其所需的概念是将(26,b1d3)从第一层剔除后得到的概念(137,a1),(24,a2),(568,a3),(15,b0c0),(3478,b2),(278,c1),(13456,c0),(58,a3d1),(14,c0d2),(2367,d3)。对上述概念进行相交运算可得到第二层概念(1,a1b0c0d2),(37,a1b2d3),(5,a3b0c0d1),(13,a1c0),(4,a2b2c0d2),(8,a3b2c1d1),(7,a1b2c1d3),(2,a2b1c1d3),(78,b2c1),(56,a3c0),(34,b2c0),(6,a3b1c0d3),(27,c1d3),(36,c0d3)。从 第二层中选取满足定义9 的中心概念并进行规则提取,如表5 所示,其中(1,a1b0c0d2),(5,a3b0c0d1),(37,a1b2d3),(4,a2b2c0d2),(8,a3b2c1d1)这5 个概念满足条件,此时可进行规则提取,此时在Exten集合中可添加元素集{1,3,4,5,7,8},故此时Exten={1,2,3,4,5,6,7,8}。至此,Exten中的元素覆盖整个论域,规则提取完毕。
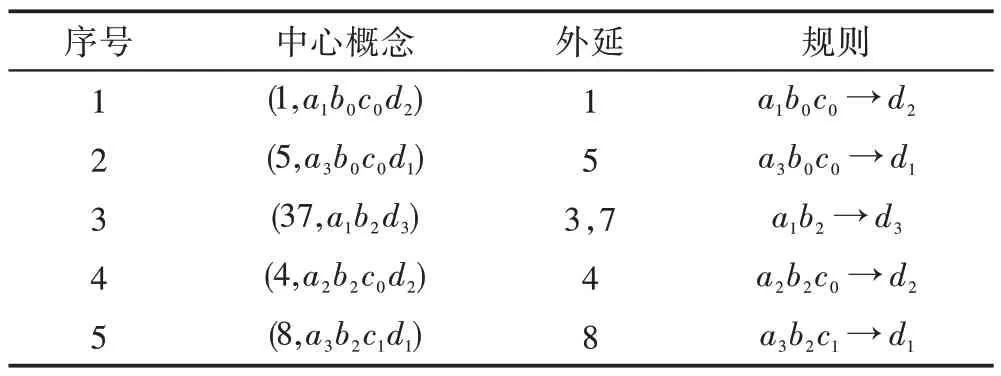
Table 5 Rule list of the second layer of central concept表5 第二层中心概念的规则列表
下面将分析算法产生的规则中是否存在冗余属性:
(1)对于规则b1→d3,根据定义7,∅↓={1,2,3,4,5,6,7,8}⊄{2,3,6,7},故规则b1→d3不存在冗余属性。
(2)对于规则a1b0c0→d2,根据定义7,故属性c0为冗余属性,因此规则a1b0c0→d2可化简为a1b0→d2。
(3)对于规则a3b0c0→d1,根据定义7,(a3b0)↓={5}⊆{5,8},,故属性c0为冗余属性,因此规则a3b0c0→d1可化简为a3b0→d1。
(4)对于规则a1b2→d3,根据定义7,{2,3,6,7},,故规则a1b2→d3不存在冗余属性。
(5)对于规则a2b2c0→d2,根据定义7,(a2b2)↓={4}⊂{1,4},因此规则a2b2c0→d2可化简为a2b2→d2。
(6)对于规则a3b2c1→d1,根据定义7,(a3b2)↓={8}⊂{5,8},因此规则a3b2c1→d1可化简为a3b2→d1。
本文算法实现了在生成概念的同时能够进行决策规则提取,直到外延集合可覆盖整个论域为止。在此过程中可能不需要生成所有概念就可将全部决策规则提取完毕。生成下一层概念时需剔除上一层概念中的中心概念,这样可减少冗余概念的生成,同时降低了算法复杂性。本算法所生成的中心概念能够直观体现出决策规则,相较传统方法中生成的单一形式概念涵盖的内容更加丰富。如图1 所示,图中圆圈为例2 中的全体概念,其中L1~L12浅灰色标注的概念为无法进行规则提取的一般概念(不包括决策内涵的概念),L13~L26的深灰色圆圈为内涵中既包括条件属性又包括决策属性的综合概念,其中用网状节点标注的概念是决策规则的中心概念,而用黑色标注的则为实际进行规则提取过程中无需生成的概念。6 个网状中心概念可代表生成的6 条决策规则。
图2 为表2 按照传统方法需分别得到条件形式概念与决策形式概念的Hasse 图,黑色虚线相连的概念体现出了条件概念与决策概念之间的包含关系,红色实线则体现出得到的决策规则。
从图1 可以看出,本文提出的综合概念、中心概念以及所要提取的决策规则都可以在一张Hasse图中清晰地表现出来,概念节点能够体现出条件与决策知识的关联性。符合人类综合考虑处理问题的特性。针对传统基于决策形式背景规则提取的方法,其构造出的Hasse图所描述的相关信息则会复杂很多。
5.2 实验测试
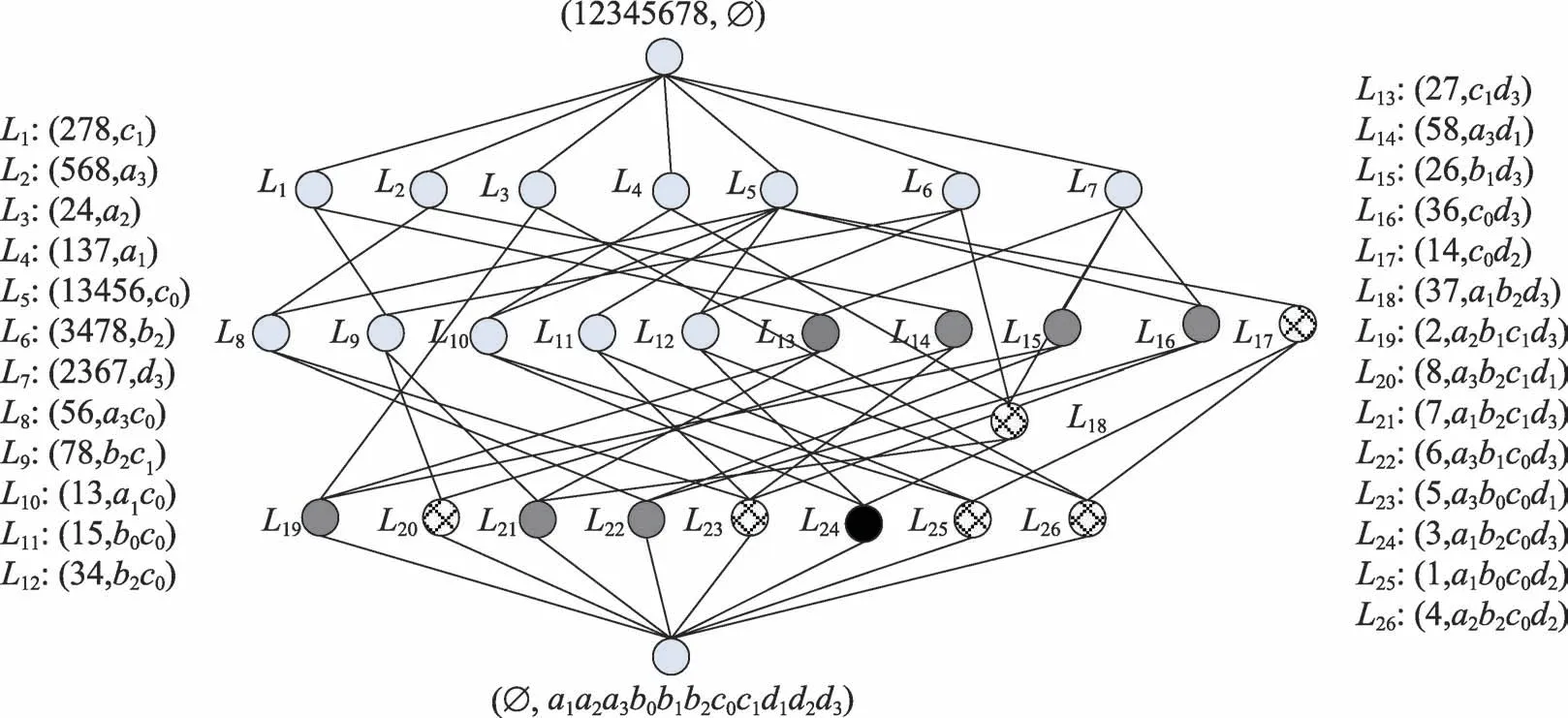
Fig.1 Hasse diagram of formal decision context图1 决策形式背景概念Hasse图
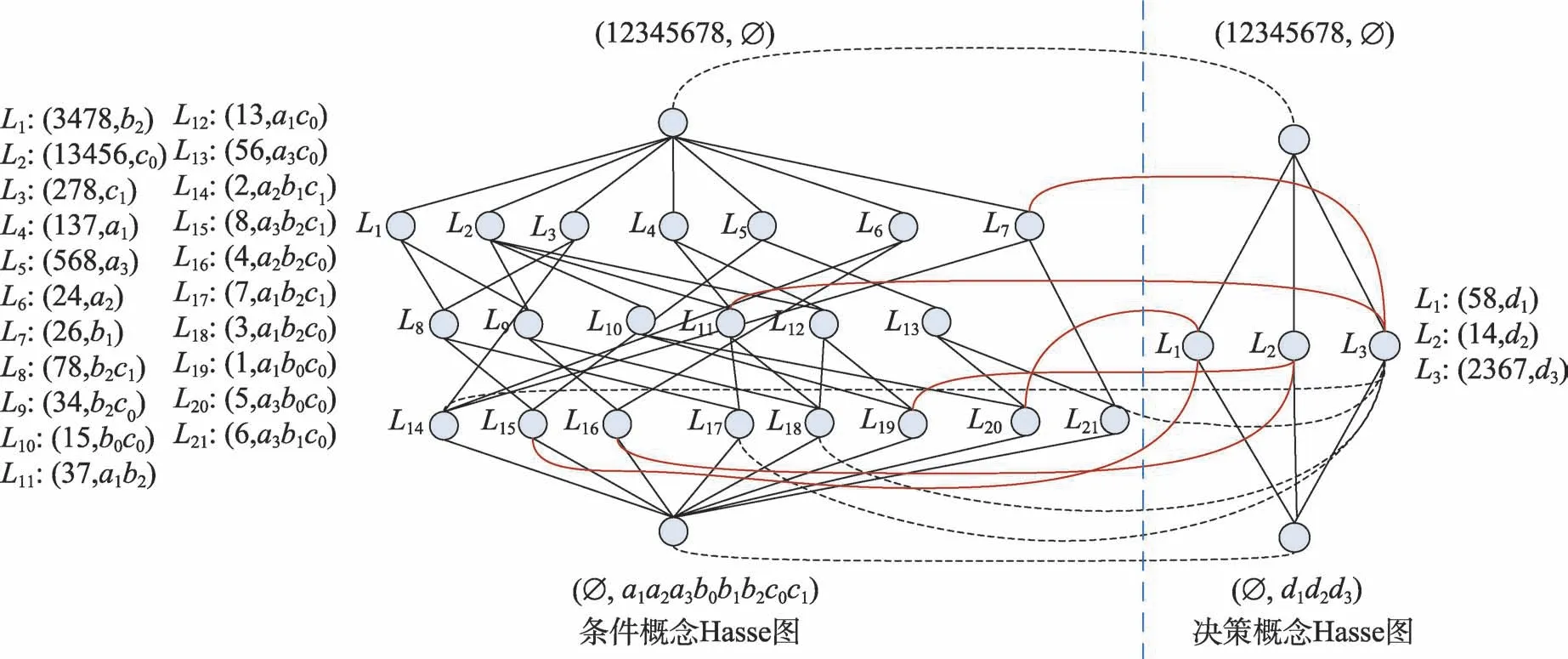
Fig.2 Hasse diagram of conditional concept and decision concept and their relationship图2 条件概念与决策概念及其关系Hasse图
通过选取以下8 组UCI 数据集来测试该算法的正确性以及有效性。利用Rosetta 软件对数据集进行离散化处理。然后,分别应用本文算法、文献[7]中的算法、文献[8]中的算法和文献[9]中的算法对数据集进行测试,以上算法均将数据集作为输入,提取到的所有规则作为输出,记录各算法所得到的约简规则个数和规则长度。其中对于文献[8]中的算法需要先将决策信息系统转化为决策形式背景来处理。最终实验对比结果如表6~表8 所示。
正确识别率[17]是由获取的规则集对每个数据集进行整体识别的正确概率。具体过程:每个数据集中各随机选取50%作为训练样本,分别应用各算法对训练样本进行规则获取并记录各自的规则集,然后利用获取到的规则集对各数据集整体进行识别。
实验分析:由上表能够看出,该算法在相同数据集上较其他算法而言,所提取到的决策规则个数更少,同时规则长度较其他算法更短,对于识别率,本文算法与文献[7]中的算法相当,略高于文献[8]、文献[9]中的算法。这可说明该算法所得到的规则集具有更强的表示能力,本文算法所得到的中心概念所涵盖的知识更加丰富,其不仅体现出了条件属性与决策属性之间的逻辑关系,同时中心概念还是形式概念与决策规则紧密结合的综合体。

Table 6 Comparison of rule number表6 规则个数对比
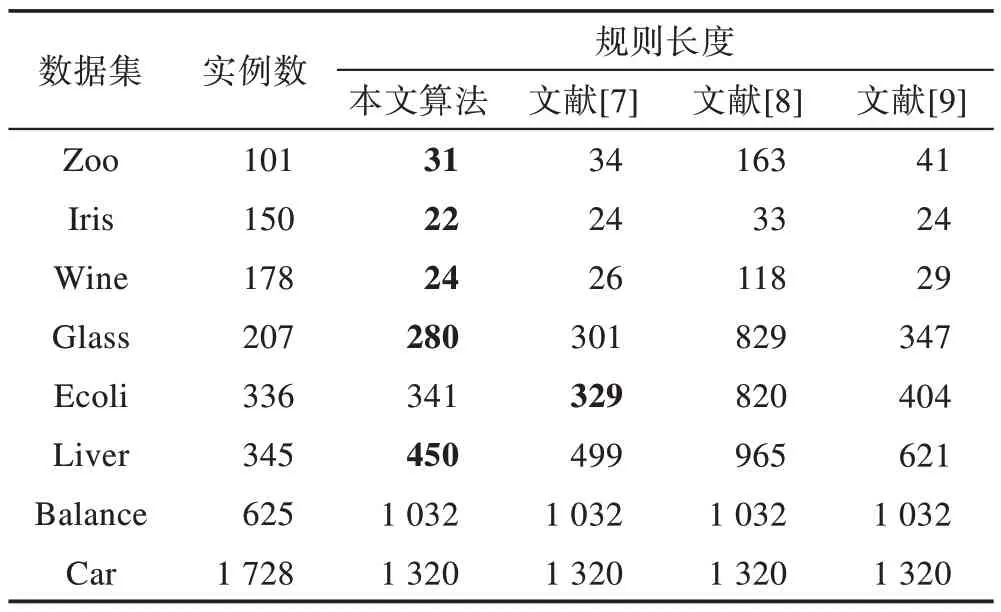
Table 7 Comparison of rule length表7 规则长度对比
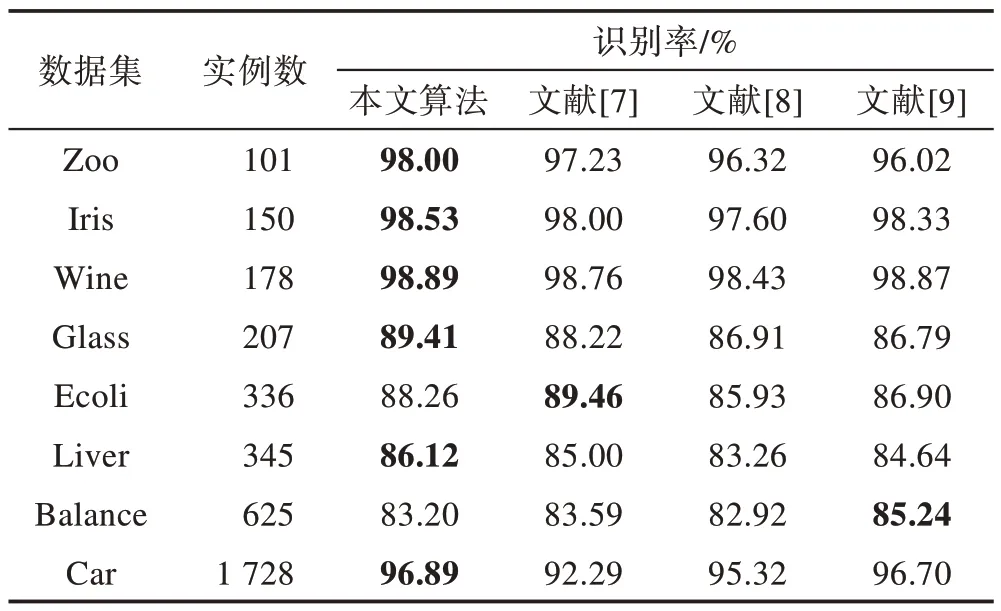
Table 8 Comparison of recognition rate表8 识别率对比
6 结束语
本文将决策信息系统作为研究对象,将决策信息系统转化成决策形式背景,决策形式背景中的决策属性参与概念的生成,内涵中包含决策属性的概念被定义为综合概念,其中满足C↓⊆d↓的综合概念被定义为中心概念。中心概念蕴含了决策信息系统中最简规则的关键信息。并且包含中心概念的Hasse图具有更加丰富且明确的意义。因此,一个决策信息系统的规则提取过程将转化为中心概念的生成以及选择的过程。此时中心概念具有丰富的研究意义。最后通过实验分析与对比说明该算法的正确性与有效性。本文算法有以下特点:(1)提出的中心概念直接蕴含了最简决策规则,较经典形式概念所表达的知识更加丰富。(2)该算法相较于其他算法来说具有较高的识别率且所提取到的规则具有较强的表示能力。并且针对协调决策信息系统而言,通过求取中心概念提取的决策规则具有完备性,能够覆盖信息系统中所有非冗余规则。文献[18]将粒计算与概念格相结合,提出了粒概念,从认知计算的角度研究了基于粒计算的认知概念学习。所有经典形式概念能通过粒概念全部求得,同时这种求取概念的方法将极大降低计算复杂性。在今后工作当中可尝试通过将粒概念与中心概念相结合,进一步优化本文算法。同时,可将本文算法拓展到不协调不完备决策信息系统的知识获取中,今后也可将其应用于语义表示及其推理,信息检索及智能推荐,以上相关研究正在进行中。
