多层网络社区发现研究综述*
2020-11-15陈可佳陈利明
陈可佳,陈利明,吴 桐
1.南京邮电大学 计算机学院,南京 210023
2.江苏省大数据安全与智能处理重点实验室,南京 210023
1 引言
社区是复杂网络的一个显著特征,即网络中的节点呈现出组(group)或者簇(cluster)的结构[1]。一般来说,社区内部节点之间的连接较紧密而社区与社区之间的连接较稀疏。社区发现是复杂网络分析的重要任务之一,有助于理解网络的内在结构和交互模式,已被广泛应用于社会学[2]、生物学[3]、计算机工程学[4]等领域。例如,在社交网络中,社区发现有助于分析个体的行为模式、信息的传播方式和网络的变化趋势[5];在生物网络中,社区发现能够帮助分析蛋白质相互作用的不同复杂功能[6];在城市交通网络中,社区发现有助于从地区之间的交通线路分析城市的影响力[7]。
传统的社区发现算法[8-9]大多用于单层网络,即网络中的节点之间仅存在单一的关系。经典的方法包括:图划分方法[10]、基于模块度的方法[11]、谱方法[12]、结构定义方法[13]等。然而,现实世界的网络往往是多层的,即节点之间可能存在多种类型的关系,每一种关系构成了一层网络。例如:社交网络中的用户之间不仅存在朋友关系,还可能存在评论关系、转发关系等。面向多层网络的社区发现逐步成为了复杂网络分析的新课题[14]。
在多层网络中发现社区的最原始做法是直接忽略关系的类型,即将多层网络视为一个单层网络,然后采用传统方法实现社区的划分。不过,此类方法损失了单层网络的结构信息,也忽视了层间的相关性,难以获得理想的划分结果。因此,多层网络社区发现的主要挑战是如何在社区发现过程中同时学习每层网络的结构信息以及层与层之间的相关性。
2 多层网络
定义1(单层网络)一个单层网络[15]可以形式化为图G=(V,E)。其中,V是节点的集合,E⊆V×V是连接节点对的边的集合。
然而,现实网络的节点之间通常呈现出多种交互关系。例如Facebook 网络中,用户之间存在关注、评论、转发等不同的交互类型。单层网络只能粗略近似这类系统,多层网络则可以进行更准确的建模。
定义2(多层网络)一个多层网络可以定义为GM={G1,G2,…,GL,EM}。L是总层数,EM是层与层之间边的集合,Gl=(Vl,El)是第l层的网络,其中第l层的节点集合Vl⊆V(V={v1,v2,…,vN},即多层网络中所有节点的集合),El⊆Vl×Vl,是第l层网络中边的集合。
许多复杂网络都可以视为多层网络,例如:多路网络、时间网络、交互网络、多维网络等。
定义3(多路网络)多路网络(multiplex network)有时也称为多重网络,是指所有层共享相同节点的多层网络,即V1=V2=…=VL=V(V={v1,v2,…,vN})。图1是一个多路网络示意图,每一层表示节点之间的一种关系,层间的虚线表示不同层的节点是对齐的。

Fig.1 Example of multiplex network图1 多路网络示例
现实世界存在大量的多路网络,例如:社交网络(用户之间存在关注、评论、转发等不同的交互)、航线网络(机场之间存在多个航空公司的航线)等。
定义4(时间网络)时间网络(temporal network)是用于表示动态网络每个时间快照的多层网络(见图2),定义为GM=(G1,G2,…,GT,EM)。其中,Gt是t时刻的网络图,Gt=(Vt,Et)。层间边EM={Et,t+1}(Et,t+1={(v,v);v∈Vt∩Vt+1})。
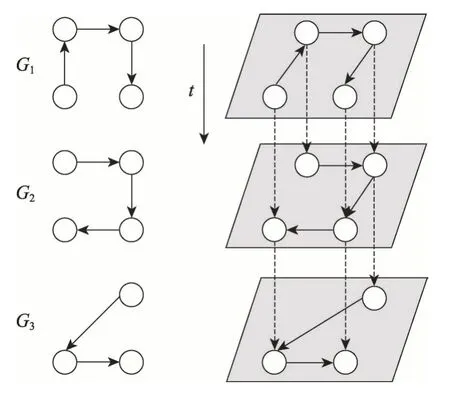
Fig.2 Example of temporal network图2 时间网络示例
定义5(交互网络)交互网络(interacting network)是指不同层之间存在相互作用的多层网络。其中,每个节点最多只存在于一层网络中,即对于任意两层网络Gi和Gj(i,j∈[1,L]且i≠j),Vi∩Vj=∅。层间边集合EM={Ei,j}(Ei,j={(vi,vj);vi∈Vi,vj∈Vj}) 。城市交通网络是一个典型的交互网络(图3),每个省及其内部城际交通可视为交互网络中的一层,两省之间的交通路线为层间的交互,反映了两省之间的相互影响力。

Fig.3 Example of interactive network图3 交互网络示例
此外,具有以下称谓的复杂网络也可视为多层网络,如:多维网络(multi-dimensional network)[16]、多关系网络(multi-relational network)[17]、多尺度网络(multi-scale network)[18]、异质信息网络(heterogeneous information network)[19]等。
表1 列举了各类多层网络在各层节点是否对齐(所有层共享相同的节点)、层间有无边以及层间边是否耦合(即每层对齐节点之间存在边)的情况。
多层网络能够更好地表示真实世界网络的拓扑结构,多层信息的融合能够大大提升复杂网络分析模型的性能。例如,将社交网络建模为多层网络能够更准确地划分社区和预测新的关系;将蛋白质网络建模为多层网络,能够找到更有效的蛋白质划分方法,发现潜在的蛋白质相互作用;将动态网络按时间片转换为多层网络,能学到时间序列信息,获得更准确的节点嵌入。

Table 1 Characteristics of different types of multi-layer networks表1 不同类型多层网络的特点
在上述多层网络中,对于多路网络的研究最为广泛。本文调研的多层网络社区发现方法大多面向多路网络,但也可以用于大部分其他类型的多层网络中。
3 传统社区发现方法
社区是复杂网络中广泛存在的结构。从拓扑结构的角度来看,社区是指一个内部连接紧密但和外部连接稀疏的子网;从信息论的角度来看,社区是指可以在相当长时间内限制信息流的模块;从机器学习的角度来看,社区可以类比为无监督聚类中的簇。社区发现研究有助于人们理解网络的内在结构和交互模式,传统方法主要面向单层网络设计,包括图划分方法、基于模块度的方法、谱方法和基于动力学的方法等[1],以及同一节点可能属于不同社区的重叠社区发现方法[20]。这些方法是多层网络社区发现的基础。
(1)图划分方法
图划分的目标在于将节点划分成k个组,使得组间边的总数(也称为切割总数)最小。K-L(Kernighan-Lin)[21]算法是最早的图划分方法之一,基本思想是先定义一个效益(gain)函数fG,表示社区内部边的总数和社区之间边的总数之差。设定随机的初始划分后,在不同社区之间互换数量相同的节点,直到fG具有最大的增量为止。
(2)基于模块度的方法
基于模块度的方法通过节点划分使得模块度(modularity)的值最大。Girvan 和Newman[2]最先给出模块度Q的定义(式(1)),即社区内的边占所有边的比例减去在同样的社区结构下随机放置社区内部的边占所有边的比例的期望值。

其中,ki和kj分别表示节点vi和节点vj的度,A是邻接矩阵,m是图中边的总数,δ(i,j)表示节点vi和vj是否在同一个社区(值为1 表示在,0 表示不在)。社区发现的过程就是模块度优化的过程,可采用贪婪算法、模拟退火算法、极值优化等策略。经典的模块度优化方法有GN(Girvan Newman)算法[2]以及适用于大规模网络的改进算法FN(fast Newman)[22]等。
(3)谱方法
谱方法利用图矩阵的谱特性来划分社区,认为特征向量越相似的节点越有可能在同一个社区。谱聚类(spectral clustering)[23]是其中最有代表性的方法,它利用节点在拉普拉斯矩阵对应的特征向量生成空间坐标,将节点映射到多维向量空间中,然后通过kmeans 等传统聚类方法对节点进行聚类,从而得到社区划分结果。
(4)基于动力学的方法
基于动力学的方法是通过网络动态过程(如随机游走力学)来划分社区。Infomap[24]是目前通过随机游走进行社区发现的一种有效方法,首先将每个节点当作独立的社区,通过构造转移概率,在图上进行随机游走生成序列,再对序列进行层次编码,最小化平均编码长度直到收敛为止。对社区编码的长度越短,社区划分的效果越好。
(5)重叠社区发现方法
上述方法检测到的社区均是不重叠的,即每个节点只被分配给一个社区。然而现实网络中,节点可以属于多个不同团体,因此出现了一系列重叠社区发现的工作[20]。如Palla 等人[25]基于团(clique)的概念提出团渗透法(clique percolation method,CPM),Lancichinetti 等人[26]提出的局部适应度最大化(local fitness maximization,LFM)方法,Ahn 等人[18]提出的基于边聚类的重叠社区发现方法以及扩展了标签传播算法(label propagation algorithm,LPA)的重叠社区发现方法CORPA(community overlap propagation algorithm)方法[27]和SLPA(speaker-listener label propagation algorithm)方法[28]。
不过,社区发现研究依然存在许多问题,包括:大部分方法的算法复杂度较高,难以处理大规模网络;有些方法(如基于模块度的方法)存在分辨率敏感的问题,难以在小规模网络上准确划分社区;有些方法(如谱方法)在稀疏网络上表现较差;许多方法需要预先设定社区的数量,难以适用于动态网络;大多数方法面向单层网络,而多层网络社区发现方法相对较少等。
本文在传统单层网络社区发现研究的基础上,重点考察多层网络中的社区发现方法。
4 多层网络社区发现方法
根据多层网络的类型及其应用场景,社区发现的目标可以是结合其他层的信息对每一层网络分别进行社区划分,也可以是融合多层网络的信息获得节点的唯一社区划分结果。
本文调研了已有的多层网络社区发现方法,根据方法的实现机制大致分为两类:基于聚合的方法和基于扩展的方法。
4.1 基于聚合的方法
基于聚合的多层网络社区发现方法又分为两种:第一种称为网络聚合,是将多层网络直接聚合成一个单层网络,然后应用传统的方法进行社区发现;第二种称为划分聚合,是在每层网络上分别进行单层社区发现,再将所有层的社区划分结果进行聚合。这两种聚合方法均只得到节点的一种社区划分结果。
4.1.1 网络聚合
基于网络聚合的方法主要是为新聚合网络中节点间的边赋予新的权重,主要有两种基本策略:一种是当任意两个节点u、v之间至少在一层网络中存在边,则聚合网络的邻接矩阵中u、v之间的连接值设为1;另一种是对邻接矩阵进行加权,u、v之间的连接权值设为它们在所有层上存在边的总数,即。这两种聚合策略最为基础,一般作为比较实验的基线方法。
Berlingerio 等人[29]基于共同邻居数越多节点越可能处于同一社区的想法,提出了基于共同邻居数的多层邻接矩阵加权策略。该策略中,的计算如下:

其中,N∙,l是某个节点在l层上的邻居数量。此外,还有其他的加权聚合策略,如基于度中心性(degree centrality)的方法等,但与式(2)相比计算复杂度较高。
不过,上述方法忽略了不同层网络具有不同的重要程度。Zhu 等人[30]定义了每层网络的重要性,如果某层网络的重要性越高,则该层的信息对其他层的影响越大。该方法采用层重要性和节点相似度得到统一的矩阵,再用单层网络社区发现方法得到最终的划分结果。
4.1.2 划分聚合
基于划分聚合的方法主要包括主模块度最大化(principal modularity maximization,PMM)[31]、共识聚类[32]、ABACUS[33]等。
Tang 等人[31]提出PMM 方法。该方法包括两步:第一步是提取每层网络的模块度矩阵的特征向量并获得级联的向量,然后采用PCA(principal component analysis)得到一个较低维的嵌入,捕获网络所有维度(层)上的主模式;第二步是对所有节点的低维嵌入表示执行k-means算法,以找出离散的社区划分。
共识聚类(consensus clustering)[32]方法先对每层网络进行社区划分,然后计算一个共识矩阵A,矩阵的元素为两个节点处于同一社区划分的网络层数。例如,两个节点在两层网络上都在同一个社区,那么Aij就为2。最后通过共识矩阵不断聚合不同层网络的社区,直到得到一个统一的社区划分。
ABACUS[33]是另一种基于划分聚合的方法,首先使用传统的社区发现方法在每层网络上分别检测社区,然后将每个节点标记为由层号ls及其在该层网络上所属的社区Cs,k组成的项(ls,Cs,k),最后应用频繁闭项集挖掘算法进行合并,得到最终的社区划分结果。
不过,由于每一层网络中节点之间的交互方式都是不同的,简单地聚合网络数据或者划分结果将会丢失每层网络的独特性。例如:基于网络聚合的方法可能会丢失每层网络的部分结构信息,而基于划分聚合的方法则忽视了不同层社区存在异质性。因此,越来越多的研究者尝试对传统方法进行扩展,以直接用于多层网络的社区发现。
4.2 基于扩展的方法
基于扩展的方法是指将单层网络的社区发现方法直接扩展到多层网络,这是目前多层网络社区发现的主流方向。本文将该类方法分为以下几种:基于多层模块度的方法、基于多层聚类的方法、基于张量分解的方法和基于多层动力学的方法。
4.2.1 基于多层模块度的方法
Mucha 等人[34]通过定义多层模块度来检测多层网络中的社区。多层模块度Qmultislice定义如下:

其中,As表示第s层网络的邻接矩阵,Cjsr表示节点vj在s层和r层之间的耦合边,表示节点vj在第s层上的度,表示第s层上的总边数,表示节点j跨越不同层的度;γs为分辨率以控制每层网络的社区规模和数量,如果节点vi和节点vj的社区分布相同,则δ(gis,gir)=1,否则为0。优化该函数进行复合社团挖掘,即每一层网络得到一个划分结果。
在此基础上,Ma 等人[35]进一步提出了多层模块度密度(式(4)),以解决模块度的分辨率限制问题。定义如下:


尽管基于多层模块度的方法能有效地对多层网络进行社区发现,但是设置的参数较多,计算复杂性较高,不太适用于大规模网络数据。
4.2.2 基于多层聚类的方法
第二类方法是将单层网络中基于节点聚类的社区发现方法扩展到多层网络。
Bródka 等人[36]提出了利用跨层边聚类系数(cross layered edge clustering coefficient,CLECC)检测多层社交网络中的社区,最终每层网络分别得到一个社区划分结果。该方法的思想是,节点之间的多层共同邻居数量越多,节点越可能在同一社区。CLECC的定义如式(6),表示为任意节点u和v(u,v∈V)的共同多层邻居数与所有多层邻居数之间的比例。

其中,Φ(∙,α)表示给定节点在至少α层上的邻居集合,α参数值可以根据网络的密度差异进行调整。
Hmimida等人[37]将单层网络社区发现方法Licod[38]扩展到多层网络,命名为Mux-Licod,利用多层网络的信息获得节点的唯一社区划分结果。Licod 的基本思想是找到称为种子的特定节点,围绕这些节点逐步发现社区。与Licod 类似,Mux-Licod 首先寻找若干领袖节点,即比大多数直接邻居具有更高度中心性的节点;然后对所有的领袖节点进行聚类,获得初始社区的集合;再计算任一节点到任意社区的所有领袖节点的多层最短路径(式(7))来估计该节点到该社区的隶属度;最后,用秩聚合(rank aggregation)函数合并相邻节点的社区隶属度得到最终的社区划分结果。

Alimadadi等人[39]扩展了单层标签传播算法(LPA),得到了多层LPA。方法首先为所有节点指定一个唯一的标签,然后逐轮更新节点的标签,直到收敛。节点标签的更新规则是:对于某一个节点,统计其所有的跨层邻居节点(式(8))的标签,将出现个数最多的标签赋给当前节点。当个数最多的标签不唯一时,则进行随机选择。

其中,Γ(i)total是节点vi在所有层上的邻居的集合,σ∈[0,1]是相似度阈值,sim(∙)是可选的相似度函数(如Jaccard 相似性度量等)。
Afsarmanesh 和Magnani[40]将单层网络社区发现方法CPM[25]扩展到多层网络。该方法首先针对多层网络定义了k-m-AND-clique,表示具有k个节点的多层网络中的子图,该子图包括来自m个不同层的至少m个不同的k-clique(大小为k的完全子图)的组合;然后将每个k-m-AND-clique 看作一个节点,如果两个cliques 之间至少共享k-1 个节点和m条边,则把它们连接起来。如果这些连通的cliques 之间至少共享m条边,则它们至少在一个社区中。
Interdonato等人[41]提出了一种多层网络上的局部社区发现方法ML-LCD(multi-layer local community detection)。在全局信息未知的情况下,通过优化局部社区函数(即内部链接密度和外部链接密度比)标识特定节点所在的社区。最后通过将特定层的贡献值与链接密度比进行线性组合将局部社区函数扩展到多层网络。
4.2.3 基于张量分解的方法
非负矩阵分解的思想已被用于单层网络社区发现[42-43]。相应地,有研究者采用张量(tensor)表示和分析多层网络的谱特性,并提出了基于张量分解的社区发现方法[44-45],用于得到唯一的社区划分结果。Esraa 等人[44]提出了一种基于张量的时域多层网络社区检测算法,用于识别和跟踪脑网络社区的结构。该框架研究跨不同兴趣区域(region of interest,ROI)构建的fMRI(functional magnetic resonance imaging)连接网络中社区的时间演变,使用张量的Tucker 分解找到最能描述社区结构的子空间。
Gauvin 等人[45]将时间网络的时变邻接矩阵表示为三向张量,将该张量近似为具有相关活动时间序列的节点社区的项之和,然后利用非负张量因子分解技术提取时间网络的社区活动结构。
4.2.4 基于多层动力学的方法
M-Infomap[46]是一种基于网络流压缩的方法,是Infomap 方法[24]在多层网络的扩展。该方法首先将多层网络表示为具有状态节点的多路复用网络,然后在网络中放置随机游走者,构造转移概率,在图上进行层内或层间随机游走生成序列,再对序列进行层次编码,最小化平均编码长度直到收敛为止。该方法最终为每一层网络得到一种社区划分结果。
LART(locally adaptive random transitions)[47]是另一种基于随机游走的方法,该方法允许游走者走到多层网络中的其他层,随机游走的转移概率取决于任意给定节点所在层之间的局部拓扑相似性。当在单层网络中游走时,LART 就会退化为经典的Walktrap[48]算法。
综上所述,在已有的多层网络社区发现方法中,一部分方法旨在得到节点的最终社区划分结果,如基于聚合的方法(PMM,ABACUS)、基于张量分解的方法等;另一部分方法则是为每层网络得到各自的划分结果,如基于多层模块度的方法、基于多层聚类的方法(CLECC、Mux-Licod)、基于动力学的方法MInfomap 等。事实上,每层网络一个社区划分意味着节点可以属于多个不同类型的社区。因此,这一系列的方法也可用于节点的重叠社区划分。然而,多层网络中的每一层也可能存在重叠的社区结构,目前这一方面的工作还很欠缺。本文仅调研到Ebrahimi等人[49]提出的基于多目标函数优化的多层网络重叠社区发现方法。
表2是本文对目前已有的16种多层网络社区发现方法的总结,主要从实现机制、层间相关性、优点、局限性、适用网络、算法复杂性等方面进行了分析和比较。

Table 2 Comparison of multi-layer network community discovery methods表2 多层网络社区发现方法的比较
5 性能比较实验
本文在11 个真实的多层网络数据集以及1 个模拟的多层网络数据集上对5 个代表性方法及其基准方法进行了验证和比较。
5.1 数据集
各数据集的节点、边和层数的统计信息见表3。其中,所有真实数据集分别来自两个多层网络数据集网站(https://comunelab.fbk.eu/data.php 和http://multilayer.it.uu.se/datasets.html),包含了不同类型、规模、层数和密集度的网络。最后一个数据集SLDS(simulated dataset 的缩写)是本文使用Bazzi 等人[50]提出的算法构造的模拟数据集。

Table 3 Statistics of datasets表3 数据集的统计信息
Florentine 网络描述了佛罗伦萨市名门望族之间存在的关系,节点表示家族,层数表示商业关系和婚姻关系。Tailorshop 网络中节点为裁缝店的工人,关系为他们之间的工作和友谊互动。Aucs 数据集描述某大学研究部门的61 名员工节点(包括教授、博士后、博士生和行政人员)之间的Facebook 关系、午餐关系、合作关系、休闲关系和工作关系。Fao Trade 是FAO(联合国粮食及农业组织)统计的世界各国食品进出口网络,其中节点表示国家,边表示各国的进出口贸易关系。Ckmpims 数据集由美国4 个城镇的246名医生组成,主要讨论网络关系对医生用药决策的影响,三层网络包括:(1)通常找谁获取用药建议;(2)经常与谁讨论;(3)与谁关系最好。London Transport 是伦敦市的交通网络,根据站点之间的连通方式分为三层:(1)地下通路;(2)地上通路;(3)DLR。Euair 数据集是欧洲航空交通网络,每层表示不同航线。Pierreauger 数据集表示了天文台科学家之间的协作关系,每一层代表一种协作任务。Ff-Tw-Yt数据集来自于Friendfeed 社交媒体,用户节点之间存在发布消息、评论消息等多种关系。Drosophila 是果蝇的基因遗传交互网络,每一层表示一种遗传交互方式。ArXiv 是研究主题为networks 的协作网络,每一种研究类别代表一层网络。
5.2 比较方法与评价指标
本文对5 个具有代表性的多层网络社区发现方法进行验证,分别为:网络聚合方法(Aggregation)[25]、PMM[26]、多层模块度(modularity quantity of multislice,Q-MS)[28]、CLECC[30]、M-Infomap[38]。此外,还增加了各方法的基准方法作为对比。基准方法是指不考虑层间交互,对每一层网络社区划分的结果求平均。
在社区发现领域,常用的评价指标有标准化互信息(normalized mutual information,NMI)[51]、模块度(modularity)[2]和调整兰德系数(adjusted Rand index,ARI)[52]等。当数据集真实的社区划分(即groudtruth)已知时,可以使用NMI 指标(式(9))和ARI 指标(式(10))来评价社区划分结果。当数据集中真实的社区结果未知时,本文采用多层网络模块度[34]作为方法的评价指标。

其中,P(wk)、P(cj)、P(wk⋂cj)分别表示样本属于聚类簇wk、cj和同时属于两者的概率。

其中,ai表示样本属于a聚类簇第i类的数量,bj表示样本属于b聚类簇第j类的数量,nij表示样本同时属于a聚类簇第i类和b聚类簇第j类的数量。
对于多层网络社区发现,可以采用类似的评价方法。由于有些方法是每层网络得到一个划分结果,对此本文是将各层的指标取均值得到最终的结果。
5.3 实验结果
图4 展示了5种方法在模拟数据集上的NMI 和ARI 比较。图中表明,Q-MS 和M-Infomap 两个方法的社区划分效果较好,它们直接在多层网络上划分社区,能够充分利用层间的关系;PMM 方法是对各层的划分结果进行聚合,未能很好利用层间相关性,效果不如前两者;CLECC 方法使用启发式的多层共同邻居数进行聚类,其效果依赖于网络的自身特性;Aggregation 方法表现最差,说明网络聚合方法丢失了最多的信息。

Fig.4 Comparison of NMI and ARI of various methods on simulated dataset图4 各方法在模拟数据集上的NMI和ARI比较
随后,本文在真实的数据集上对各方法在多层模块度Qmultislice指标上的表现进行了比较(见表4)。表中的加粗数字表示性能最优,下划线数字表示性能次优。结果表明,Q-MS 和M-Infomap 在不同规模的数据集上的总体表现依然最优;PMM 在小规模稠密网络中的划分效果更好,但在大规模稀疏网络中的效果较差;CLECC 的表现最不稳定,说明该方法对于网络类型的依赖程度较高。
图5 对比了各方法及其基准方法在Ff-Tw-Yt 数据集上的多层模块度指标值。
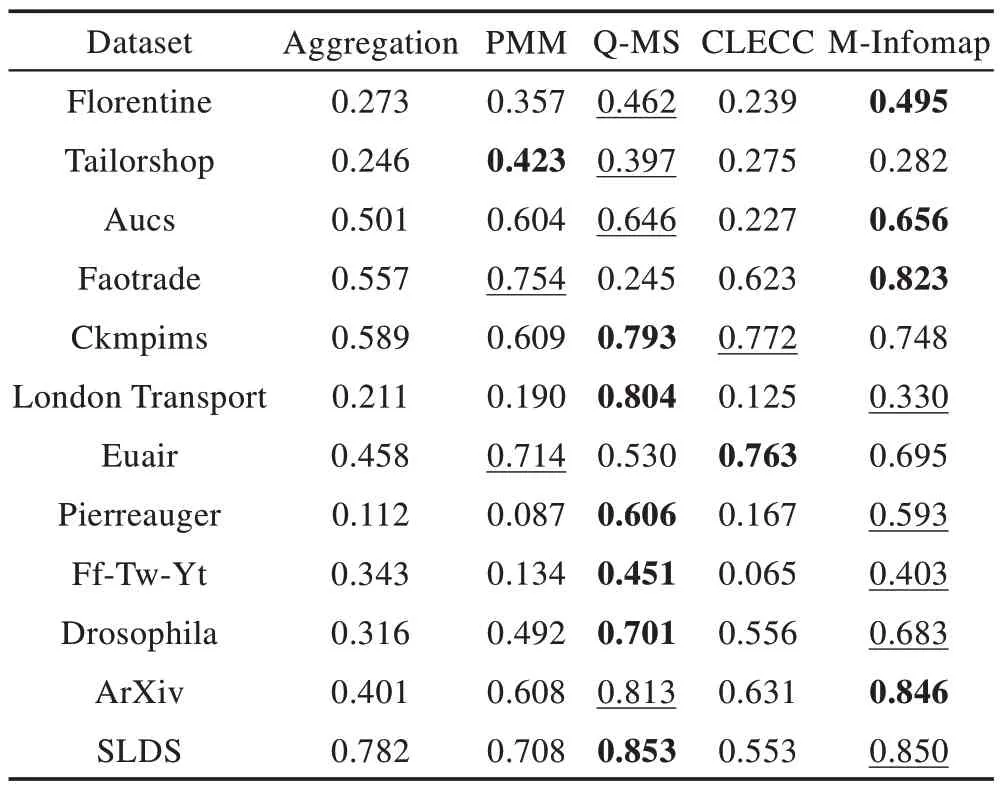
Table 4 Comparison of Qmultislice of various methods on datasets表4 各方法在数据集上的多层模块度比较
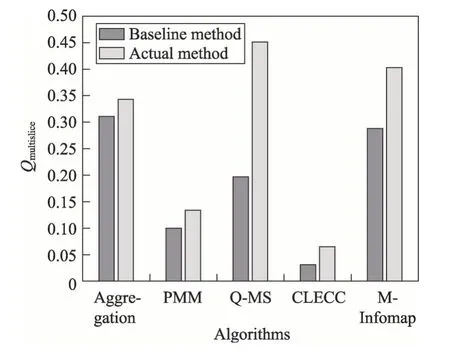
Fig.5 Comparison of Qmultislice of various methods on Ff-Tw-Yt dataset图5 各方法在Ff-Tw-Yt数据集上的多层模块度比较
结果表明,与未考虑层间相关性的基准方法相比,每种方法的多层模块度指标都有了显著提高,说明学习层间相关性对多层网络社区发现的性能至关重要。其中,Q-MS 和M-Infomap 方法的提升幅度最为明显,说明这两种方法能较好地学到层间相关性。
最后,本文比较了各方法在Ff-Tw-Yt 数据集上的运行时间(见图6)。其中,Aggregation 方法是将多层聚合为一层之后再进行社区发现,大大简化了网络结构,因此运行最快;Q-MS 通过计算节点分配社区后的模块度增益来优化目标函数,收敛也较快;PMM 通过PCA 对特征向量降维,可有效减少聚类时间;M-Infomap 通过随机游走来捕获层内和层间的信息流,时间复杂度较高;CLECC 通过删除边聚集系数最小的边来获得层级结构,每次删除之后需要重新计算各边的系数,因此时间复杂度非常高。
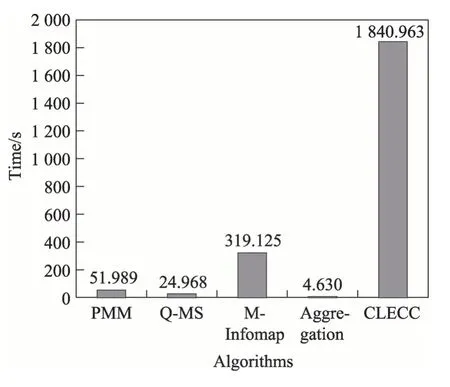
Fig.6 Comparison of running time of various methods on Ff-Tw-Yt dataset图6 各方法在Ff-Tw-Yt数据集上的运行时间比较
6 结束语
本文系统性地介绍了多层网络社区发现的研究现状,总结了已有方法的特点,并通过实验对代表性方法的性能进行验证和比较。
尽管多层网络社区发现已经引起了越来越多的关注,但由于网络数据在类型、规模、演变方面的复杂性,目前该领域仍然存在诸多的挑战。主要体现在以下三方面。
(1)如何更好地学习网络结构和层间关系
已有的方法直接使用网络的拓扑结构信息(例如多层邻居、多层模块度、跨层随机游走等),其性能严重依赖于网络的类型,而且是启发式地学习层间关系。目前,随着网络表示学习技术(特别是图神经网络[53])的兴起,节点的自动嵌入技术能够为多层网络社区发现带来新的思路。
(2)如何提高可扩展性,以适应大规模网络
大部分已有方法(如基于张量分解的方法)的复杂性较高,难以扩展至大规模网络。最近有方法采用粗化策略并保持原始的社区效应,用于在大规模多层网络中发现社区,具有一定的可行性[54]。此外,图池化[55]方法也能起到类似的作用。
(3)如何适应动态变化的多层网络
网络在不断动态变化,节点的社区结构也应不断调整。大部分已有的方法是针对静态网络设计,有些方法[44-45]是将单层动态网络转化为多层网络来学习社区结构,但是针对动态的多层网络社区发现方法目前还很欠缺。
