神威国产处理器应用程序的并行参数自动寻优*

刘 徐，肖志勇，甘 霖，徐敬蘅，陈宏博

1.江南大学 物联网工程学院，江苏 无锡 214122

2.国家超级计算无锡中心，江苏 无锡 214131

3.清华大学 计算机科学与技术系，北京 100084

1 引言

以超级计算机为代表的高性能计算技术一直以来都是计算机科学研究与应用的重要方向，也是服务于医学、军事、航天等各个领域的计算保障。“神威·太湖之光”作为世界上第一台峰值性能超过每秒十亿亿次双精度浮点计算能力的超级计算机[1]，2016—2017 年4 次成为世界最快超算系统，与“天河2 号”共同实现了我国国产超算在世界超算系统排名上的十连贯。在2019 年5 月最新一期全球超级计算机Top500 中排名第三[2]，也是目前我国最快的超级计算机。“神威·太湖之光”全面采用了国产异构众核处理器申威26010，全机由40 960 个处理器组成。

申威26010 处理器由主从核结构构成，故部署在“神威·太湖之光”上的应用程序是针对神威架构做的优化程序。针对主从核的结构，它有进程级和线程级的并行优化，其中主从核内的数据结构和分配对应用程序算法的性能影响较大。使用参数对应用程序数据进行划分，将数据合理分配在申威26010 处理器主从核上，能充分利用申威异构众核处理器从而有效提升应用程序性能。通常来说，随机选取的参数往往无法获得最优性能，而采取遍历或者人工寻找最优参数的方式又耗时太长且开销过大。此时，采取合适的方法自动获取最优参数，充分利用申威处理器的计算能力就显得非常重要。

有限差分模板计算用于求解偏微分方程，是科学计算内一个重要分支。它具有易于实现、通用性强等优点，被广泛应用于地震模拟、石油勘探、全球大气模式数值模拟等多个领域[3-6]。但该算法计算密度高，访存跨度大，通信和同步开销大，CPU 利用低，使得算法在实际应用中的性能难以得到保障。因此，提高该算法的可扩展性，减少通信和同步开销就成为研究人员的重点工作。本文将该算法部署在申威26010 异构众核处理器上，通过合理分配有限差分模板计算算法数据，充分利用神威处理器强大的计算能力来提升该算法性能。以二维有限差分模板计算算法为例，寻找合理的消息传递接口（message passing interface，MPI）规模参数和从核规模参数，寻址空间达10 亿次方，又由于每运行一次二维有限差分模板计算算法需要近2 分钟，采用穷举法需要20 亿分钟，显然开销过大，而随机选择不需要耗时但往往得不到合适解。故本文采用遗传算法来解决该NP 问题，在合理时间内寻找合理的参数解。

遗传算法是根据自然界进化规律，即适者生存、优胜劣汰的繁衍规律推演出来的一种进化算法。它通过遗传算子，如交叉算子、变异算子等获取优良基因，在整个搜索空间内寻找产生最优染色体[7]。相比于其他进化算法，遗传算法具有天生并行性，全局寻优能力强等特点，对解决大规模并行机上的组合优化问题非常有效[8-9]。虽然现有的基于GPU 的遗传算法模型在理论上可以适用于异构众核处理器架构，但是由于并行架构[10]的不同特性、通信复杂度、适应度函数计算复杂以及编译器优化差异的影响[11]，使得优化性能和加速比很难得到保证。

基于以上问题，本文面向申威异构众核处理器，提出一种基于遗传算法的并行参数自动寻优方法。为充分利用申威26010 异构众核处理器优势，提升有限差分模板计算应用程序的性能，本文采用遗传算法将有限差分模板计算的数据进行合理分割并部署在申威26010 异构众核处理器的主从核上。本文工作的主要贡献有：

（1）在“神威·太湖之光”上实现消息传递接口（MPI）数据规模参数（TX，TY）和从核规模参数（NX，NY）自动寻优，与编译器自动分配相比大大提高了工作效率。

（2）面向异构众核申威26010 处理器，第一次基于遗传算法实现超大规模自适应并行参数优化。

（3）并行参数（TX，TY，NX，NY） 寻址空间超过10 亿次方，使用该方法成功解决了一个在国产异构众核处理器下多参数寻优的NP 问题。在寻址空间内寻找合理参数，并在“神威·太湖之光”平台下进行有限差分模板计算测试，与编译系统自动分配结果相比获得了10.79 倍的加速比，对国产异构多核超级计算机上的并行优化具有指导意义。

2 背景和相关工作

2.1 “神威·太湖之光”和SW26010 异构众核处理器

“神威·太湖之光”是世界领先的超级计算机，全系统峰值运算速度每秒12.54 亿亿次，持续运算速度每秒9.3 亿亿次，性能功耗比每瓦60.5 亿次，与其他相同量级计算机相比节能60%以上[1]。“神威·太湖之光”是世界上首台峰值运算性能超过10 亿亿次量级超级计算机，也是我国第一台全部采用国产处理器构建的超级计算机[12]。

“神威·太湖之光”搭载着40 960 个“申威26010”异构众核处理器。SW26010 基本架构如图1 所示，每个处理器包含4 个运算核组（computational groups，CG）共260 个计算核心。每个核组包括一个内存控制器（memory controller，MC）和65 个运算核心，即一个8×8 的计算处理单元（central processing elements，CPE）和一个管理处理单元（manage processing element，MPE）[13]。CPE 和MPE 都是完整的64 位RISC（reduced instruction set computing）内核，但它们在计算时处理不同的任务。MPE 支持完整的中断函数、内存管理和无序问题执行，用于管理、任务调度和数据通信；CPE 用于实现超高性能和计算任务。核组内MPI 和CPE 通过主、从核的方式实现并行协作，核组间通过片上网络（network-on-chip，NOC）进行连接，系统接口用于与片外系统进行连接。

Fig.1 SW26010 multi-core processor structure diagram图1 申威26010众核处理器结构图

SW26010 众核处理器与其他多核或众核处理器不同。在内存层次结构上，MPE 采用传统32 KB L1指令cache，32 KB L1 数据cache 和256 KB L2 指令和数据混合cache，但CPE 仅16 KB L1 指令cache，并用64 KB 的从核局部存储空间（local data memory，LDM）作为用户控制快速缓冲。另外，每个CPE 包含控制单元、数据传输单元、8 行通信总线、8 列通信总线。8行、8 列的通信总线为8×8 的CPE 间的寄存器通信提供条件，实现CPE 数据共享，减少访存时间，有效提高带宽[1，14]。申威异构众核处理器的架构特点使得从核之间的数据相互隔离，这有利于追求极致性能，但也带来了更多编程问题。可以看出，应用程序数据的分割将直接决定通信、访存和计算情况，严重影响应用程序的性能[15-16]。

2.2 相关工作

本文研究的重点是针对“神威·太湖之光”平台上应用程序数据规模参数进行自动优化。本节讨论了前人关于超级计算机并行参数优化问题和遗传算法应用方向的一些相关工作，并提出面向“神威·太湖之光”的遗传算法参数自动寻优方法。

近年来，对并行非功能参数进行自动调优越来越流行，在典型大搜索空间内在合理时间内寻找高性能参数值具有重要意义[17-20]。Arcuri 和Fraser[21]探讨了参数调优对算法性能的影响并给出指导原则。Durillo 和Gschwandtner 等人[22]提出一种并行程序的多目标分区域感知优化方法。Wu 和Weimer 等人[23]基于变量的方法自动发现和探索深层参数。Cosenza和Durillo 等人[24]提出一种基于结构学习的Stencil 自动调优方法。Zhou 和He等人[25]提出了一种矢量并行蚁群算法模型解决多核SIMD（single instruction multiple data）并行ACO（ant colony optimization）问题。Khmelev 和Kochetov[26]用遗传算法解决分割送货车辆路径问题。Zavoianu 和Bramerdorfer等人[27]优化电机驱动器的性能，有效减少计算时间，降低运行功耗。Singh 等人[28]提出一种用于异构计算机系统中调度工作流应用的方法。Ghosn等人[29]提出了一种基于确定性和随机性的开放式车间调度并行遗传算法等。

从以上相关工作可以看出，随着计算机从单芯片系统发展到集群系统，遗传算法也从小规模串行走向大规模并行，并被广泛应用于解决各种超大规模并行优化问题。本文面向国产申威26010 异构众核处理器，基于遗传算法完成大规模多并行参数自动调优。该方法对部署在“神威·太湖之光”上应用程序数据进行合理划分，采用遗传算法完成大规模并行参数寻优，以期充分利用主核和从核资源，获取应用程序最高性能。

2.3 本文工作

遗传算法是通过模拟自然进化法则来解决各种优化问题的一种有效算法。它通过随机初始化一系列种群，以非确定性的方式搜索整个问题空间。对所有问题参数（基因）进行编码，通过适应度来选择判断基因优劣，并选择优良基因遗传给下一代，从而提高种群的平均质量。遗传算法中每一个后代都通过一定概率发生反转、变异，有效避免过早收敛到局部最优解。通过选择和组合优良个体的迭代过程产生更好的个体，直到找到最优解或者达到停止条件。

结合申威26010 众核处理器结构特征，将应用程序计算量较大的部分部署在从核上进行加速，部署在从核上的应用程序需要对应用程序进行二级数据分块，第一级分块得到MPI 规模参数（TX，TY），第二级分块得到从核数据规模参数（NX，NY）。

本文以二维有限差分模板计算为例，测试和比较模板计算的性能。本文中遗传算法流程图如图2所示，基本操作包括以下部分：

编码：本文将MPI 数据规模参数（TX，TY）和从核数据规模参数（NX，NY）作为“染色体基因”。对基因进行二进制编码，随机初始化生成种群。

Fig.2 Flow diagram of algorithm图2 算法流程图

选择：遗传算法通过适应度函数衡量染色体优劣。本文利用CPE 并行计算获得适应度，通过轮盘赌算法选择出“优良基因”，充分体现了“适者生存、优胜劣汰”的自然进化法则。

交叉：自然界通过继承“父亲”和“母亲”的优良基因获得“进化”。本文对轮盘赌算法选择的“优良基因”进行单点交叉，获取下一代基因。

变异：基因突变是产生新个体，跳出局部最优的有效方式。本文设定变异概率，从种群中选择个体，随机选取变异点进行变异。

运行本文遗传算法程序，自动修改应用程序的数据分割参数，采用一系列遗传操作对两级参数自动寻优，寻找合适的数据分块加速应用程序。

3 神威并行参数自动寻优

3.1 染色体编码和种群初始化

本文提出对参数组合的自动寻优方法，使用遗传算法来解决参数的组合优化问题。为更好地解释本文方法，以二维有限差分模板计算算法为例进行描述和分析。根据SW26010 异构众核处理器的结构特征可知，应用程序部署在主从核上，主核与从核上数据的分配将严重影响到应用程序的性能。本文将单个主核上处理的数据量TX×TY与单个从核上处理的数据量NX×NY作为染色体完成遗传操作。遗传算法不能直接处理问题空间内参数组合，将参数集的编码作为基因输入，将4 个基因参数（TX，TY，NX，NY）用二进制编码表示，用染色体形式表示优化问题的可行解。

TX、TY作为MPI 数据规模参数，本文中取值为0 到1 023 内的整数值，故选择9 位二进制串，即000000000 到111111111 进行编码；基因NX、NY是从核数据规格参数取值，本文取值为0 到127 内整数，选择用6 位二进制串，即000000 到111111 进行编码表示。将4 个参数编码为一个30 位的基因串，即染色体用于表示个体所有参数组合解。

本文采用随机方法产生初始种群。把二进制编码解码为十进制数，二进制编码解码位实数的映射公式如下：

其中，M表示由二进制编码对应的十进制数值，xi位对应基因变量的二进制表示，bi和ai表示对应基因变量二进制的上下限，l为二进制基因串长度，本文取值为30。另外，受神威系统结构影响，基因NY取值必须为8的整数倍，基因TY取值必须为8×NY的整数倍。

3.2 适应度函数

适应度函数是用来评判基因优劣的标准，个体适应度高低决定了是否将其基因遗传给下一代。本文在申威国产处理器上测试二维有限差分模板计算性能，计算性能作为适应度反馈给遗传函数，性能高则适应度高，遗传给下一代的概率就更大。

二维有限差分模板计算是一种基于偏微分方程的数值离散方法，被广泛应用于解决地震波模拟、石油勘探等各种非线性问题，本文中有限差分的具体计算形式如图3 所示，每个中心单元的取值由上下左右8 个单元的取值所确定。

Fig.3 2D finite difference Stencil calculation diagram图3 二维有限差分模板计算示意图

另外，本文还对有限差分的单元进行矢量化，并加载到4 个SIMD 寄存器，同时对4 个SIMD 寄存器进行处理，即可以同时计算4 个单元，具体计算形式如图4 所示。

Fig.4 Parallel computation of 4 SIMD registers图4 4 个SIMD 寄存器并行计算示意图

3.3 并行模块

本文采用主从动态并行方式进行异构并行编程，即通过MPI+Athread 的方式使用主核和从核，主核主要负责任务分配，从核进行并行计算和写回计算结果。每个主核（MPE）上可运行一个MPI 进程，Athread 是神威系统特有的线程库，用来控制从核阵列。该方式适合从核计算时间不固定的情况，采用两级主从并行方式进行大规模并行计算，第一级是进程级别的主从并行，第二级是异构众核处理器核组内部的主从并行。

主核部分伪代码如算法1 所示，MPI 实现多个主核之间的并行，Athread 提供封装函数库和API 接口，Athread 从核并行程序中主核进程内容包括相应头文件、共享变量定义、从核口函数类型声明、初始化从核软件环境、启动线程、回收线程、终止从核环境。

算法1主核伪代码

从核进程内包括相应头文件、共享变量定义、从核局存变量声明、从核线程绑定、发起DMA（direct memory access）读数据、完成计算、发起DMA 写回数据。具体从核部分伪代码如算法2 所示。

算法2从核伪代码

3.4 选择和繁衍

本文使用轮盘赌算法进行选择操作，保留更优良的染色体作为双亲染色体为下一代提供基因。选择的过程是达尔文优胜劣汰、适者生存自然进化规律的体现。经轮盘赌选择得到的双亲染色体通过交叉算子将优良基因遗传给下一代，但只进行交叉操作容易导致过早收敛进入局部最优，故本文还通过变异的方法跳出局部最优寻找其他更优解。

轮盘赌算法的基本思想是根据适应度函数值来评判个体被选择的概率，适应度越高，被选择的概率越大。首先，计算种群适应度，求得每个染色体被选择的概率：

其中，f（xi）为适应度函数值，n为个体总数，求取每个染色体的累积概率：

此时，生成0 到1 内的随机数r，并判断r在累积概率内的所在区间，得到相应染色体。按照以上规则，采用轮盘赌算法选取在当前适应度函数下更可能存活的个体，在本文中即选择出性能更高的染色体。被选中的染色体成为双亲进行交叉操作，将优良基因遗传给下一代。

3.4.1 交叉算子

交叉操作是遗传算法中最主要的遗传操作，通过组合双亲染色体的优良基因特性得到新的下一代个体，体现了信息交换和优胜劣汰的思想。本文采用了单点交叉法，如图5 所示，在轮盘赌算法选出的双亲染色体中随机选择交叉点，两条染色体交叉位之后的基因进行位置交换产生新的两条染色体，重复此操作直到达到一个种群的个体数。具体算法实现的伪代码如下：

算法3交叉算子伪代码

Fig.5 Crossover operator图5 交叉算子

3.4.2 变异算子

变异操作是解决遗传算法陷入局部最优的有效方法，通常有根据概率随机选择染色体或固定染色体两种变异方式。本文采用了前一种方式，以1%的概率进行变异操作。从种群中随机选择一个染色体，对选中的染色体随机选择一个变异点进行变异。算法如下：

算法4变异算子伪代码

4 性能结果与分析

4.1 二维有限差分模板计算测试

本例测试在申威26010 国产异构众核处理器下进行，为简单化测试模型，测试函数采取为边界值等于2 的二维有限差分模板计算模型。使用64 个从核进行并行计算，采用遗传算法自动分配MPI 规格参数（TX，TY）和从核规格参数（NX，NY）。通过比较执行时间、性能、加速比3 个评价指标，评价基于遗传算法自动选取的最优并行参数对于面向“神威·太湖之光”的二维有限差分模板计算算法性能的影响。受“神威·太湖之光”平台限制，遗传算法部分使用Python 实现，性能并行计算适应度函数部分使用C 语言实现。

本例实验中遗传算法内的控制参数选用固定值，交叉率为80%，变异率为2%，种群大小为50，迭代次数选取50 次。图6 展示了在该条件下随迭代次数增加，性能提升情况。MPI 参数取值为TX=243，TY=1 156，从核规格参数取值为NX=44，NY=72 时，性能趋于稳定值，达到最高性能13.744 306 GFlop/s。

为提供真实的性能分析，本文通过Roofline模型[9]来分析程序的性能上界，该方法在特定平台上寻找特定应用程序性能上界。二维有限差分模板计算量为11 Flop，SW26010 每个核组的测量带宽近似为26 GB/s[20]，故在SW26010 单核心组上的二维有限差分模板计算算法的性能上界近似为：

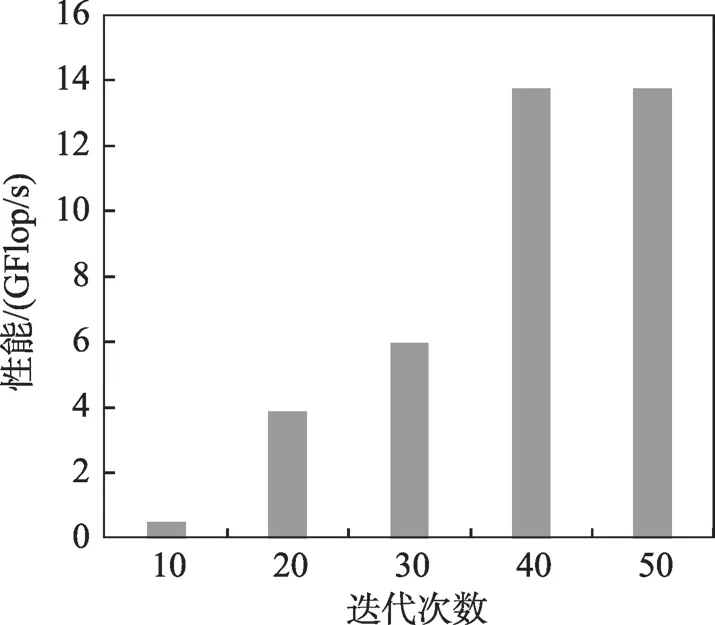
Fig.6 Graph of performance changes with increase of genetic iterations图6 遗传代数增加性能变化图

但上述性能上界的计算包括一些在实际二维有限差分模板计算程序中不可能实现的强假设。首先，二维有限差分数据存在冗余读取；其次，二维有限差分模板计算数据不对齐使得数据访问带宽不能达到上限；最后，onchip 操作将阻塞主存访问。故在实际情况下，难以达到性能上界的80%[30]。本文最高性能达到性能上界的77%，效果较好。

为考察从核并行和SIMD 并行计算对性能影响，通过表1 展示了编译系统自动分配的运行时间，使用10 次随机选取参数中运行时间最少的与使用遗传算法得到的并行参数实现64 个从核运行和加入SIMD的运行时间对比。从表1 看出，编译系统自动分配将导致数据的分散化，运行时间为0.569 065 s，之后3组实验数据都以此为基础计算对应的加速比。随机选择参数难以得到最优分配参数，10 次随机选择参数中最小的运行时间为0.160 922 s，达到3.53 倍加速比。使用本文遗传算法自动寻优最优并行参数运行时间为0.075 774 s，加速比可达7.51，明显高于随机分配值。此外，本文使用遗传算法得到的最优并行参数进一步加入了SIMD 处理，运行时间为0.052 724 s，加速比为10.79。

Table 1 Comparison of running time and acceleration ratio表1 运行时间、加速比对比表

4.2 三维逆时偏移成像算法测试

为进一步证明本文方法正确性与实用性，对三维逆时偏移成像算法进行测试与分析。地震成像是石油工业中寻找储蓄层位置的基本工具，通过生成地形图像探究地质结构。地震建模中首先产生声波并记录距离震源一定距离处地表的响应；然后对记录数据采用某种算法进一步重建传播介质的性质[3]。描述地震波传播要非常精确的复杂波方程。逆时偏移成像算法（reverse time migration，RTM）利用双程波生成地形图像，在高陡构造、盐下成像中呈现显著优势，是目前地震建模中最常用的偏移算法之一[4-5]。图7 为本文RTM 算法流程图。从流程图中可知RTM算法的主要原理是边界值为2和边界值为4的三维有限差分模板计算。具体计算方式如图8 所示。

本文在“神威·太湖”上实现RTM 算法并对该算法进行分析，由于在计算过程中仅有一个方向的数据连续存储在内存中，这种非均匀内存访问导致非常大的时间开销。本文提出使用遗传算法对影响RTM 算法性能严重的三维从核规格参数进行自动寻优，充分利用硬件资源以减少时间开销。

本例中，将三维从核规格参数组合的二进制码作为染色体。受申威异构众核处理器架构和RTM 算法条件限制，三维参数NX、NY、NZ的取值变化范围分别为[1，500]、[1，1 000]和[1，1 000]内的整数，其中NX必须为4 的倍数，并且NX、NY、NZ的乘积不超过3×107。采用RTM 算法运行时间的倒数作为适应度函数，即当算法运行时间越短，对应染色体适应度越高。本例中遗传算法迭代次数为30 次，其他控制参数均与二维有限差分模板计算算法相同。

图9 展示了使用本文方法当迭代次数增加时RTM 算法的优化结果。从图中可以看出，随迭代次数增加，算法性能有效提高，并在第21 次迭代时取得最优效果，然后保持稳定值。

表2 展示了系统自动分配参数、10 次随机选择取参数中运行时间最少的与采用本文自动寻优方法得到的参数三种情况下三维逆时偏移成像算法运行时间与加速比，加速比以编译系统自动分配的数据为基础进行计算比较。从表中可以看出，与系统自动分配参数相比，采用本文方法自动寻优得到的最优参数使三维逆时偏移成像算法达到了6.31倍加速比。

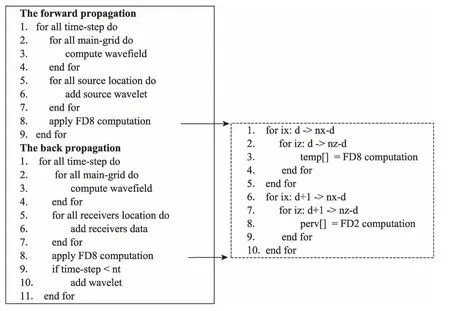
Fig.7 Flow chart of RTM algorithm图7 RTM 算法流程图

Fig.8 3D finite difference Tencil calculation diagram图8 三维有限差分模板计算示意图

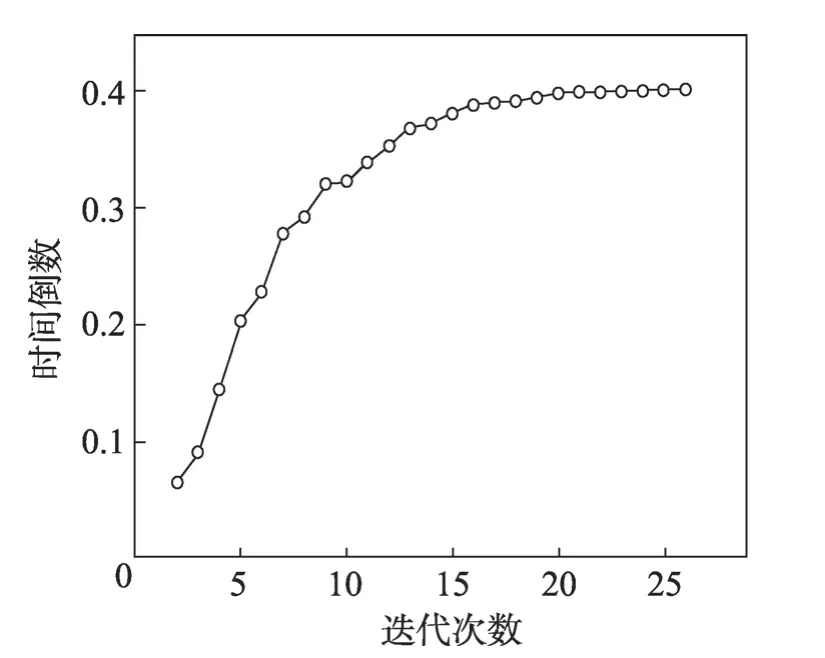
Fig.9 Change in inverse of RTM running time as the number of iterations increases图9 随迭代次数增加RTM 运行时间倒数变化图

Table 2 Comparison of running time and acceleration ratio of RTM algorithm表2 RTM 运行时间与加速比对比表

5 结论

本文对“神威·太湖之光”深层架构进行研究和分析，对国产申威异构众核处理器上的并行参数进行研究，首次提出了面向神威国产处理器的并行参数自动寻优方法。该方法基于遗传算法实现了并行参数自动寻优，通过牺牲一定时间在10 亿次寻址空间中寻找较优的参数，在时间和性能中寻找平衡，有效解决了一个申威众核异构处理器上数据规模参数分配的NP 问题。自动获取的并行参数对MPI 数据规模和从核数据规模进行合理划分，在“神威·太湖之光”上进行二维有限差分模板计算算法测试和三维逆时偏移成像算法测试，与编译系统自动分配参数相比最高分别达到了10.79 倍和6.31 倍的加速比。对于有限差分模板计算、逆时偏移成像等算法在异构多核超级计算机上的并行优化具有指导意义。