结合二次聚类编码的生成式可逆信息隐藏方法*

赵 迪，邵利平，任平安

陕西师范大学 计算机科学学院，西安 710119

1 引言

传统信息隐藏，例如密写[1-2]、分存[3]和水印[4]等，通常采用修改式嵌密，会在嵌密载体中留下修改痕迹，从而难以抵抗密写分析器的检测。

为解决该问题，人们提出了搜索式无载体信息隐藏[5-7]。相对于修改式嵌密，搜索式无载体信息隐藏通过选取适合的自然未修改载体来表达秘密信息。但这类方法需从大规模自然载体数据集中寻找适合的未修改载体，搜索代价高且单载体嵌密容量极低，即使借助倒排索引，其存储和维护代价也十分高昂。

除了搜索式无载体信息隐藏，一些学者也提出了纹理生成式信息隐藏[8-12]，通过生成自然界中不存在的图像，使得攻击者找不到追溯的根源；主要包括纹理构造式信息隐藏[8-9]和纹理合成式信息隐藏[10-12]。其中纹理构造式信息隐藏主要通过模拟纹理生成的方式来产生类自然纹理，用于对秘密信息进行掩盖。相对于纹理构造式信息隐藏，纹理合成式隐藏可产生纹理更为复杂和逼真的类自然纹理图像，这类方法通常将秘密信息直接编码为自然纹理小块，通过自然纹理小块拼接的方式来生成与给定自然样例图像相似的含密纹理图像。为生成含密纹理，纹理合成式信息隐藏通常采用缝合线算法将相邻小块进行拼接[10-11]，将指定位置出发连接重叠区域相邻像素差异最小的误差线作为边界，把两侧位于不同分块的像素融合在一起，但特定位置起始的最小误差线并不一定是重叠区域所有像素差异最小的缝合线，因此容易产生缝合痕迹，从而无法对秘密信息进行掩盖。为减少拼接痕迹和提高视觉质量，文献[12]提出了最小误差纹理合成算法，选取重叠区域像素差异和最小的误差线作为缝合线并依据最小拼接代价优先原则进行相邻小块拼接；为提高抗攻击能力，文献[12]还将给定样例图像随机截取的样例纹理小块进行差异均值聚类，通过选取聚类中心位置最接近的样本小块来构造编码样本小块。文献[12]尽管可产生差异最小的拼接纹理并通过选取具有最大类间差异的聚类中心位置的编码样本小块来提高含密纹理图像的抗攻击能力，但从根本上依然无法消除拼接痕迹。

另外，纹理构造式和纹理合成式信息隐藏生成的纹理图像都较为简单，从而不能对秘密信息进行有效掩盖。

为生成有意义掩体图像，一些文献还给出了基于马赛克拼图的信息隐藏策略[13-17]。这类方法将密图划分的小块作为字典，通过对有意义掩体图像的相似块替换来隐藏密图。例如，文献[13]利用相似块替换将密图伪装成公开图像，文献[14]进一步将密图划分为四份放在预先选择的四张掩体图中。为避免文献[13-14]预先选取与密图相似的公开图像作为掩体，文献[15]将密图和掩体小块按标准差升序排列，通过引入可逆颜色变换将密图小块伪装成掩体小块。文献[16]引入优化分类阈值算法改进文献[14]，使得生成伪装图像和目标图像的均方差最小。但文献[13-16]都采用修改式嵌密来嵌入重构秘密信息图像的相关参数，因此不可避免地存在固有的修改痕迹。为避免修改式嵌密，文献[17]利用任意选取的圆形图像直接表达秘密信息，通过马赛克拼图来产生有意义含密掩体。基于马赛克拼图的信息隐藏尽管可产生有意义含密掩体，但马赛克间存在着固有的拼接痕迹，从而导致生成嵌密掩体的视觉质量较差。另外这类方法生成的含密掩体在嵌密时会损失部分视觉质量，从而导致嵌密后的掩体无法恢复。

针对以上文献存在的问题，并借鉴于纸张印刷中广泛采用的调整单色墨水浓淡产生连续色调的半色调印刷方法，本文提出了一种结合二次聚类编码的生成式可逆信息隐藏方法，所提方法将随机产生的不同灰度阶的二值噪点小块作为候选样本小块，经由二次聚类编码滤除不同灰度阶的相似样本小块，来筛选同一灰度阶的编码样本小块用于二值秘密信息的编码表示。通过生成的随机二值参考图结合随机嵌密位置来放置不同灰度阶的编码样本小块，产生含密掩体。在提取时，首先由密钥按二次聚类编码产生编码样本小块，然后结合二值参考图和嵌密位置提取二值秘密信息比特。

相对于既有工作，本文的主要贡献在于：

（1）相比于搜索式无载体信息隐藏[5-7]，本文方法所需的样本小块均由密钥产生，无需数据库，无需在信道中传递大量含密自然载体。

（2）相比于纹理生成式信息隐藏[8-12]，本文方法能生成视觉质量良好的有意义图像，不存在拼接痕迹，并且具有较好的抗攻击能力。

（3）相比于传统马赛克拼图信息隐藏[13-17]，本文方法不存在任何修改式嵌入，不会遗留拼接痕迹，可靠性高。

（4）无论秘密信息如何嵌入，本文方法的含密掩体均可等质量地无损恢复为原始掩体图像，且嵌入和提取过程完全依赖于用户密钥，具有较高的安全性。

（5）借鉴文献[12]通过选取具有最大类间差异的聚类中心位置编码样本小块来提高含密纹理图像的抗攻击能力，本文进一步给出了二次聚类编码，用于拉开不同灰度阶样本小块间的距离和滤除不同灰度阶的相似样本小块的影响，同时保证同灰度阶的不同编码样本小块具有最大的类间差异以提高抗攻击能力。

2 所提方法

图1 给出了本文所提方法的流程框图。在嵌密时，首先输入p阶掩体图像C=（cx，y）M×N，cx，y∈{0，1，…，p-1}并生成黑色噪点样本小块，i=0，1，…，p-1，j=0，1，…，r-1，其中r为C中每个灰度阶生成的样本小块数量；其次样本小块经由二次聚类编码产生编码样本小块Ak，0，Ak，1，k=0，1，…，p-1；再次生成随机二值参考图S和嵌密坐标序列T，结合S、T和C，从Ak，0，Ak，1，k=0，1，…，p-1 中选取合适的编码样本小块来编码秘密信息比特位串B以及生成含密掩体Cfinal。在提取时，首先构造与嵌密过程中同样的编码样本小块Ak，0，Ak，1，k=0，1，…，p-1，二值参考图S和嵌密坐标序列T，然后结合S和T重构秘密信息比特位串B并恢复原掩体。

2.1 结合二次聚类编码的生成式可逆信息隐藏方法

在嵌入阶段主要涉及的处理环节有二次聚类编码和含密掩体图像生成。

2.1.1 二次聚类编码

文献[12]通过选取聚类中心位置最接近的样本小块构造编码样本小块，使得所提方法相对于文献[10-11]进一步提高了抗攻击能力。借鉴文献[12]的差异均值聚类，本文进一步给出了构造编码样本小块的二次聚类编码算法，用于拉开不同灰度阶样本小块间的距离和滤除不同灰度阶相似样本小块的影响，同时保证同一灰度阶的编码样本小块对秘密信息具有充分的表达能力且具有最大的类间差异以提高编码样本小块的抗攻击能力。

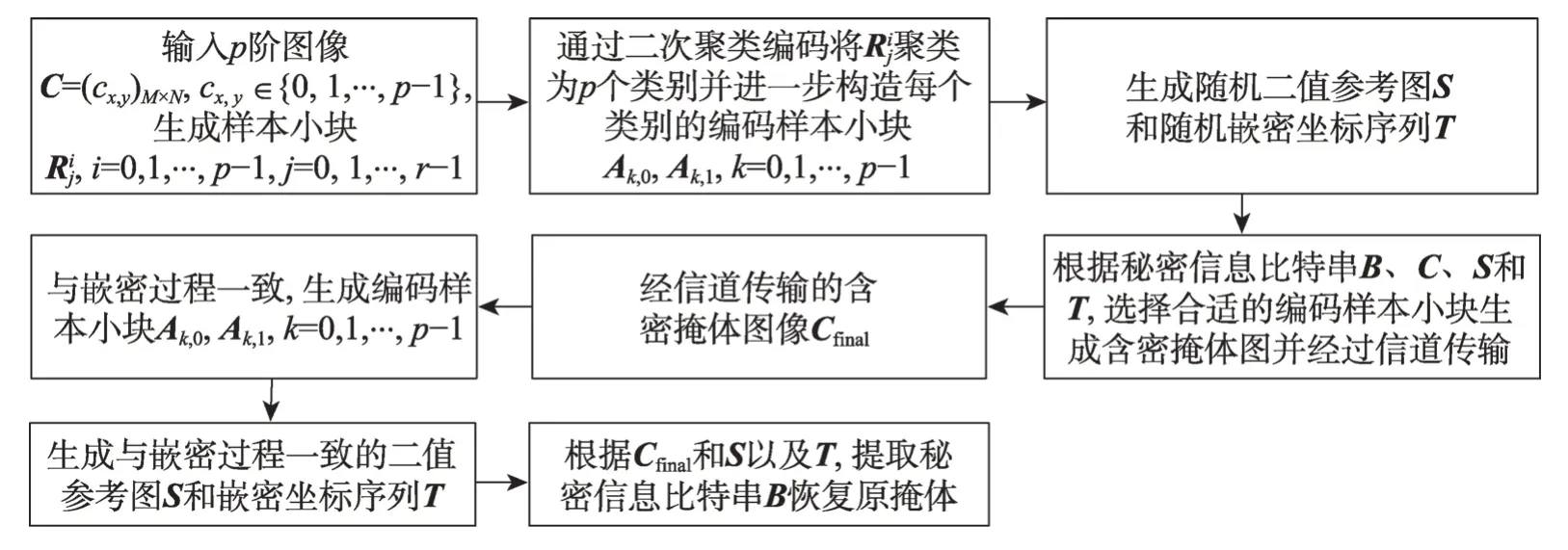
Fig.1 Diagram of generating information hiding method through quadratic clustering coding图1 结合二次聚类编码的生成式信息隐藏方法框图

二次聚类编码的过程是：首先由用户密钥产生不同灰度阶的黑色噪点样本小块；其次通过二次聚类算法中的第一重聚类筛选算法将黑色噪点样本小块划分为多个类别，通过划分类别识别出不同灰度阶的相似样本小块并进一步滤除不同灰度阶的相似样本小块的影响；最后进一步通过第二重聚类筛选算法构造同一灰度阶的编码样本小块，在保证同一灰度阶的编码样本小块对不同秘密信息充分表达能力的同时，进一步拉开同灰度阶编码样本小块的距离，以提高编码样本小块对抗攻击时的区分度。

本文之所以通过用户密钥产生样本小块而不采用搜索式无载体信息隐藏构建的数据库样本，其原因是：搜索式无载体信息隐藏采用自然未修改载体来表达秘密信息，由于自然未修改载体对不相关秘密信息的表达能力十分有限，导致搜索式无载体信息隐藏需构建大数据库并涉及大量含密载体在信道中密集传输，即使借助倒排索引也无法缓解其构建、搜索和传输代价。而本文方法是直接构建表达二值秘密信息的样本小块，并且针对掩体图像的所有灰度阶像素，都提供了对应的灰度阶编码样本小块，因此拥有对秘密信息的充分表达能力。并且通过用户密钥来生成不同灰度阶的样本小块，使得收发方仅需共享相同的密钥，即可生成同样的样本小块，避免了信道中密集传输样本小块所带来的安全风险，同时也不需要构建搜索式无载体信息隐藏涉及的大数据库。

记输入分辨率为M×N像素的p阶灰度掩体图像C=（cx，y）M×N，cx，y∈{0，1，…，p-1}，则生成黑色噪点样本小块的具体过程是：

取用户密钥k1作为随机数种子，对C中的每个灰度阶Gi=i，i=0，1，…，p-1 随机生成r个分辨率为H×W的样本小块，i=0，1，…，p-1，j=0，1，…，r-1，其中由Gi生成的具体过程可描述为式（1）：

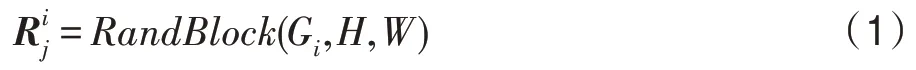
式（1）中，随机样本小块生成函数RandBlock（Gi，H，W）具体执行的功能如算法1 所示。

算法1随机样本小块生成算法

步骤1初始化分辨率为H×W的空白图像，其中H、W满足的约束如式（2）；按式（3）计算上生成的黑色像素点的数量X。

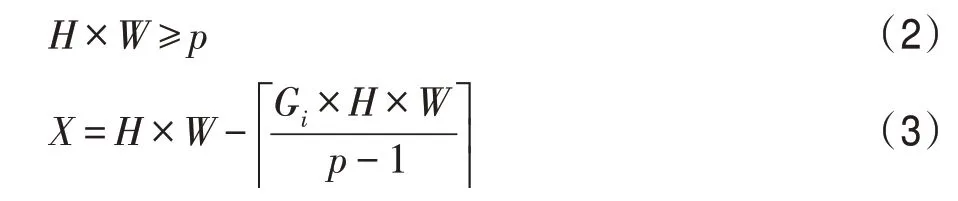
步骤2随机生成长度为X的随机坐标序列U=（（xk，yk））X，其中（xk，yk）∈H×W且U中坐标两两不等。

步骤3对U中的每个坐标（xk，yk），置上的元素rxk，yk=0 直至U序列中的所有坐标处理完毕，将输出。

在算法1 中，用户密钥k1用于同步嵌入和提取过程随机样本小块，i=0，1，…，p-1，j=0，1，…，r-1 的生成过程。使得只有正确的用户密钥k1，才能保证生成的样本小块完全一致。

进一步，以用户密钥k2为随机数种子，将生成的p×r个样本小块按均值聚类为p个类别S0，S1，…，Sp-1，在每个类别Sk中剔除灰度值不为Gk的样本小块，其中k=0，1，…，p-1，将其称为二次聚类编码第一重聚类筛选算法，如算法2 所示。

算法2二次聚类编码第一重聚类筛选算法

步骤1对每个Gi，i=0，1，…，p-1 随机生成的r个分辨率为H×W的样本小块，j=0，1，…，r-1，根据用户密钥k2从中随机选择一个样本小块作为初始聚类中心Dk，其中k=0，1，…，p-1。

步骤2按式（4）计算到Dk=（ds，t）H×W的距离，其中i，k=0，1，…，p-1，j=0，1，…，r-1，按距离最小找到所属的类别Sind，ind∈{0，1，…，p-1}，将其加入到Sind中。

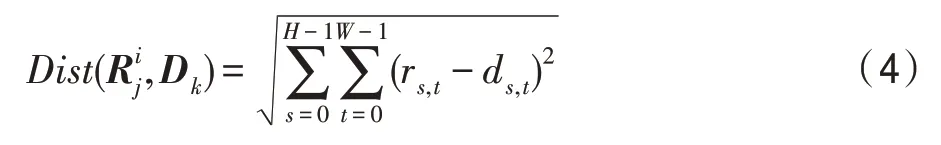
步骤3记是Sk中的第i个样本小块，|Sk|是Sk中的样本小块数量，这里可按式（5）计算Sk中所有样本小块的均值Mk，然后按式（6）寻找最优样本小块，按式（7）更新聚类中心Dk，其中i=0，1，…，|Sk|-1，k=0，1，…，p-1。

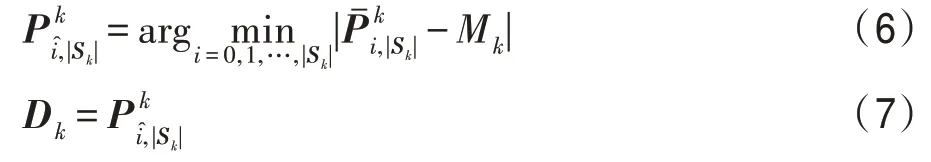
步骤4重复执行步骤2 到步骤3，直至聚类过程趋于稳定或达到指定的迭代次数，输出S0，S1，…，Sp-1，将Sk中灰度值不为Gk的样本小块删除。

在算法2 中，用户密钥k2用于同步嵌入和提取过程中二次聚类编码的初始聚类中心，使得通信双方由相同的聚类中心出发，从而产生一致的聚类结果。

算法2 将Sk中灰度均值不为Gk的样本小块删除的目的是拉开不同灰度阶样本小块的距离，避免不同灰度阶的样本小块中存在的相似样本小块，以降低样本小块在遭受攻击时的误判概率。

进一步对每个集合Sk按均值聚类划分为两个类别Sk，0和Sk，1，从中分别选取离Sk，0和Sk，1聚类中心位置最近的样本小块作为编码样本小块Ak，0，Ak，1，其中k=0，1，…，p-1，将其称之为二次聚类编码第二重聚类筛选算法，其具体处理过程和算法2 类似，第二重聚类筛选算法的目的是最大化同一灰度阶样本小块的编码距离，从而降低同一阶灰度样本在遭受攻击时的误判概率以提高编码样本小块的抗攻击能力。

传统纹理生成式信息隐藏方法[10-11]利用不同类别的纹理小块代表不同的秘密信息，但只是简单地从同一类别中随机筛选样本小块来表达秘密信息，未考虑到同类样本小块在对抗攻击时的差异性，因此在遭受攻击时极易出现类别提取错误。为提高抗攻击能力，文献[12]将给定样本图像随机截取的样本小块进行差异均值聚类，选取离每个类别聚类中心位置最近的样本小块作为编码样本小块，来降低攻击所导致的类别提取错误。本文借鉴文献[12]的聚类方法，将样本小块通过两次聚类过程编码为具有最大类间差异的编码样本小块，使其在遭受攻击时不易产生类别识别偏差，从而具有较强的抗攻击能力。文献[12]虽然提高了抗攻击能力，但该方法首先要将代表秘密信息的小块放置在空白图像上，随后进行纹理小块的拼接形成对秘密信息的掩盖，不能生成有意义的含密掩体图像；而本文所生成的含密掩体为无拼接痕迹的有意义图像，可更好地解决该问题。

2.1.2 含密掩体图像生成

以用户密钥k3为随机数种子生成分辨率为M×N的二值参考图S=（sx，y）M×N，sx，y∈{0，1}，记秘密信息是长度为l的二值比特位串B=（bi）l，bi∈{0，1}，由用户密钥k4确定随机坐标序列T=（（xi，yi））l，其中（xi，yi）∈M×N且T中坐标两两不等，算法3 给出了秘密信息嵌入和含密掩体图生成算法，其中k3生成的二值参考图S=（sx，y）M×N用于对嵌入的秘密信息进行嵌入前加密；k4生成的嵌密坐标序列T=（（xi，yi））l，用于决定秘密信息的嵌入位置，若没有正确的k3和k4将无法准确地提取秘密信息。

算法3秘密信息嵌入和含密掩体图生成算法

步骤1初始化含密掩体图，对C=（cx，y）M×N中的每个元素cx，y，以（x∙H，y∙W）为左上角坐标，按含密掩体图生成策略在Cfinal上放置H×W的样本小块。

（1）若（x，y）∉T，置k为cx，y处的k值，然后从Ak，0，Ak，1随机选取一个，作为放置的H×W样本小块。

（2）若（x，y）∈T且（x，y）=（xi，yi），置k为cx，y处的k值，按式（8）确定编码样本小块Ak，b′i中的，然后将Ak，b′i作为放置的分辨率为H×W像素的样本小块。

步骤2反复执行步骤1，直至B中的所有元素bi处理完毕，将生成的Cfinal作为含密掩体输出。

为保证隐藏策略对密钥的完全依赖性，密钥k1、k2、k3、k4由Logistic 混沌映射按式（9）生成，其中系统参数μ∈[3.57，4.00]，初始密钥x0∈（0，1）和消除暂态效应的滤除迭代次数IT，IT＞0 由通信双方约定。

取式（9）连续生成的4 个随机数作为用户密钥k1、k2、k3、k4，而k1、k2、k3、k4又进一步影响样本小块，i=0，1，…，p-1，j=0，1，…，r-1、二次聚类编码样本小块Ak，0，Ak，1，k=0，1，…，p-1、二值参考图S和随机嵌密坐标序列T的生成，使得本文嵌入过程和通信双方约定的密钥具有完全的依赖性。

2.2 结合二次聚类编码的生成式可逆信息提取方法

在提取时，同隐藏方法一致，首先输入初始系统参数μ∈[3.57，4.00]，密钥x0∈（0，1）和消除暂态效应的滤除迭代次数IT，IT＞0，取Logistic 混沌映射连续生成的4 个随机数作为用户密钥k1、k2、k3、k4。

其次按第2.1 节生成编码样本小块Ak，0，Ak，1，k=0，1，…，p-1，并以k3为随机数种子生成分辨率为M×N的二值参考图S=（sx，y）M×N，根据秘密信息的长度控制参数l，由k4确定随机坐标序列T=（（xi，yi））l。

再次遍历含密坐标序列T=（（xi，yi））l，输入分辨率为M∙H×N∙W的含密掩体图，根据随机坐标序列T=（（xi，yi））l，按秘密信息提取策略提取秘密信息B，并由Cfinal重构原始掩体图像C=（cx，y）M×N，其具体方法如算法4 所示。

算法4秘密信息提取和掩体图像恢复算法

步骤1对于T=（（xi，yi））l中的每个（xi，yi），将其作为左上角坐标，从Cfinal中截取分辨率为H×W的样本小块R=（rs，t）H×W，按式（10）从Ak，b′i，k=0，1，…，p-1，b′i=0，1寻找与R=（rs，t）H×M最接近的编码样本小块。

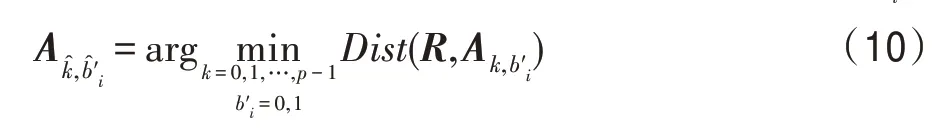
步骤2参考S按式（11）提取bi：

步骤3反复执行步骤1 和步骤2，直到T=（（xi，yi））l中的所有坐标处理完毕，将B=（bi）l输出作为提取的秘密信息。

步骤4将含密掩体图分割为M×N个分辨率为H×W的小块Cx，y，x=0，1，…，M-1，y=0，1，…，N-1，将Cx，y对应的灰度均值gx，y作为c′x，y，将，x=0，1，…，M-1，y=0，1，…，N-1 作 为 恢复的掩体图像。

提取阶段的密钥k1、k2、k3、k4也由Logistic 混沌映射按式（9）生成，和隐藏阶段的k1、k2、k3、k4保持一致，而k1、k2、k3、k4也进一步影响着样本小块、二次聚类编码样本小块Ak，0，Ak，1，k=0，1，…，p-1、二值参考图S和随机嵌密坐标序列T的生成，使得本文提取过程也和通信双方约定的密钥具有完全的依赖性。

3 本文方法的完整步骤

结合第2 章的工作，以下给出完整的结合二次聚类编码的生成式可逆信息隐藏策略，分别如算法5 和算法6 所示。

算法5信息隐藏算法

步骤1输入由通信双方约定的系统参数μ∈[3.57，4.00]，初始密钥x0∈（0，1）和消除暂态效应的滤除迭代次数IT，IT＞0，取Logistic 混沌映射连续生成的4 个随机数作为用户密钥k1、k2、k3、k4。

步骤2输入p阶灰度图像C=（cx，y）M×N，以k1为随机数种子，按算法1 生成样本小块，i=0，1，…p-1，j=0，1，…，r-1。

步骤3以k2为随机数种子，按算法2 将，i=0，1，…，p-1，j=0，1，…，r-1聚类为p个类别S0，S1，…，Sp-1。

步骤4对每个集合Sk进一步聚类划分为两个类别Sk，0和Sk，1，从中分别选取离Sk，0和Sk，1聚类中心位置最近的样本小块作为编码样本小块Ak，0，Ak，1，其中k=0，1，…，p-1。

步骤5以k3为随机数种子生成分辨率为M×N的二值参考图S=（sx，y）M×N，sx，y∈{0，1}，由k4确定随机坐标序列T=（（xi，yi））l，（xi，yi）∈M×N且T中坐标两两不等。

步骤6初始化含密掩体图，按算法3 嵌入秘密信息B并生成含密掩体图Cfinal。

步骤7输出含密掩体图。

算法6信息提取算法

步骤1输入系统参数μ∈[3.57，4.00]，密钥x0∈（0，1）和消除暂态效应的滤除迭代次数IT，IT＞0，取Logistic 混沌映射连续生成的4 个随机数作为用户密钥k1、k2、k3、k4。

步骤2以k1为随机数种子，按算法1 生成样本小块，i=0，1，…，p-1，j=0，1，…，r-1。

步骤3以k2为随机数种子，按算法2 将，j=0，1，…，r-1 聚类为p个类别S0，S1，…，Sp-1。

步骤4对每个集合Sk进一步通过聚类划分为两个类别Sk，0和Sk，1，从中分别选取离Sk，0和Sk，1聚类中心位置最近的样本小块作为编码样本小块Ak，0，Ak，1，其中k=0，1，…，p-1。

步骤5以k3为随机数种子生成分辨率为M×N的二值参考图S=（sx，y）M×N，sx，y∈{0，1}，根据秘密信息的长度控制参数l，由k4确定随机坐标序列T=（（xi，yi））l，（xi，yi）∈M×N且T中坐标两两不等。

步骤6输入含密掩体图，按算法4 提取秘密信息B并恢复掩体图像。

同纹理生成式信息隐藏[8-12]和马赛克拼图信息隐藏[13-17]相比，由于本文编码样本小块都是由均匀分布的随机二值噪点构成，不会存在明显的拼接痕迹，也不涉及任何修改式嵌入且所提方法无论秘密信息如何嵌入，含密掩体均可等质量地恢复原始掩体图像，通过引入二次聚类编码，也提高了含密掩体的抗攻击能力；由于本文方法是通过二值噪点小块的空间分辨率来表达掩体像素的灰度分辨率，从而将多灰度阶掩体图转化为二值图像，并且针对掩体图像的所有灰度阶像素，二值秘密信息的两种状态，都提供了对应灰度阶的编码样本小块且拥有对二值秘密信息的完全表达能力，在嵌密容量内无论嵌入多少比特秘密信息，嵌密后均不会损失原掩体的视觉质量，可准确重建原始掩体；此外，所提方法的用户密钥k1、k2、k3、k4均由logistic 混沌映射的初始参数x0、μ和IT生成，对密钥具备完全的依赖性，若无法提供x0、μ和IT，将无法提取出秘密信息。

4 实验

实验测试环境为Windows 10 操作系统，CPU 为Intel®CoreTMi5-6600，主频为3.31 GHz，内存为8.00 GB，实验编程语言为JAVA jdk 1.8.0_65。

采用峰值信噪比（peak signal to noise rate，PSNR）和误码率（bit error rate，BER）分别对嵌入提取的秘密信息图像视觉质量以及秘密信息恢复质量进行评价，PSNR 的计算式如式（12）所示：

式中，MSE为均方误差（mean square error），计算式如式（13）所示：

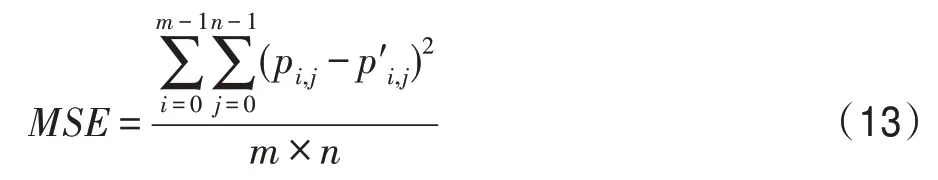
式中，pi，j、p′i，j为待比较图像像素值，m×n为图像分辨率。

误码率BER的计算式如式（14）所示：

式中，le为提取错误的秘密信息比特数；ln为秘密信息长度。

图2 给出了实验图样，实验中选取分辨率为256×256 像素的灰度图像（图2（a）、图2（b））作为原始图像，由图2（a）、图2（b）经误差扩散法生成的16 级灰度图像（图2（c）、图2（d））作为实验输入的灰度掩体图像；为验证本文方法秘密信息嵌入不会对掩体图像造成任何视觉质量损失，分别选取分辨率为450×120 像素的二值图像（图2（e））和分辨率为300×100 像素的二值图像（图2（f））作为嵌入的秘密信息图像。

Fig.2 Experiment images图2 实验图样

以下分别通过正确性实验、密钥依赖性实验、抗攻击实验、掩体恢复实验、二次聚类编码有效性验证实验和与传统方法的对比实验对所提策略的性能进行检验。

4.1 正确性验证实验

为验证所提策略的正确性，取样本小块的分辨率为8×8，按算法5 嵌入秘密信息并生成含密掩体图像，然后按算法6 从含密掩体图像中提取秘密信息。

表1 给出了实验参数，图3（a）～图3（d）分别为生成的分辨率为2 048×2 048 像素的含密掩体图像，图4（a）～图4（d）为图3（a）～图3（d）对应的恢复秘密信息。

由表1、图3 和图4 可看出，所提方法可生成视觉质量较好的含密掩体图像，并能通过正确密钥提取秘密信息且提取的秘密信息相对于原秘密信息的BER为0，PSNR为无穷大，说明秘密信息能完整恢复。

4.2 密钥依赖性实验

为验证所提策略对密钥的依赖性，对正确性验证实验中的实验参数x0和μ进行微小修改，然后按算法6从含密掩体图3（a）、图3（b）中恢复出秘密信息。

Table 1 Correctness verification experiment parameters表1 正确性验证实验参数

Fig.3 Stego cover images in correctness verification experiment图3 正确性验证实验的含密掩体图

Fig.4 Recovered secret information图4 恢复的秘密信息

表2 给出了密钥依赖性实验的实验参数，表3 和表4 进一步验证了用户密钥k1、k2、k3、k4微小改变时的密钥依赖性验证实验结果，其中“—”表示未修改，对应的恢复秘密信息如图5（a）～图5（p）所示。

从表2、表3、表4 和图5 可以看出，无论是对x0和μ还是对k1、k2、k3、k4分别进行任意微小改动，提取出的秘密信息相对于原秘密信息的PSNR始终在3 dB 左右，从而无法获取任何有价值的信息；BER均在50%左右，具有较大的不确定性，说明只有提供正确的密钥才能获取正确的秘密信息，而错误的密钥将无法提取秘密信息。

Table 2 Initial key dependency verification experiment parameters表2 初始密钥依赖性验证实验参数

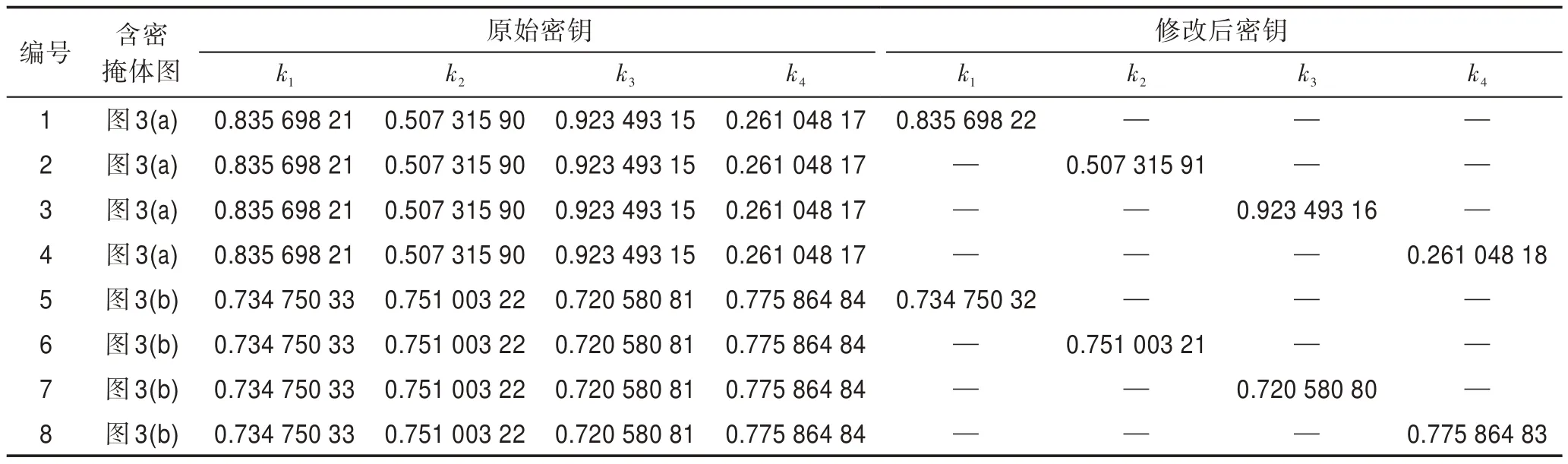
Table 3 User keys k1，k2，k3，k4 dependency verification experiment parameters表3 用户密钥k1、k2、k3、k4 依赖性验证实验参数

Table 4 User keys k1，k2，k3，k4 dependency verification experiment results表4 用户密钥k1、k2、k3、k4 依赖性验证实验结果

4.3 抗攻击实验

为验证所提方法的抗攻击性能，分别对正确性实验中生成的含密掩体图像图3（a）和图3（c）进行攻击，包括：（1）剪裁攻击，对含密掩体图像随机剪裁不同数量的分辨率为50×50 像素的马赛克小块；（2）加噪攻击，对含密掩体图像添加不同强度的椒盐噪声；（3）画线攻击，在含密掩体图像上进行随机画线。

表5 给出了抗攻击实验的实验参数，图6 和图7分别给出了攻击后的含密掩体和恢复的秘密信息。其中，图6（a）～图6（d）为剪裁攻击，图6（e）～图6（h）为椒盐噪声攻击，图6（i）、图6（j）为随机画线攻击。

由图6、图7 和表5 可以看出，尽管含密掩体图像遭受了不同程度的剪裁攻击、椒盐噪声攻击以及随机画线攻击，但提取的秘密信息的BER均在3%以下，说明所提方法的二次聚类编码策略可有效地分担各种攻击，具备良好的抗攻击能力。

Fig.5 Recovered secret information in key dependency verification experiment图5 密钥依赖性验证实验恢复秘密信息

4.4 掩体恢复实验

为验证含密掩体可等质量无损地恢复为原始掩体图像，以正确性验证实验图3 生成的含密掩体图3（a）～图3（d）为例，按算法4 重构掩体图像。

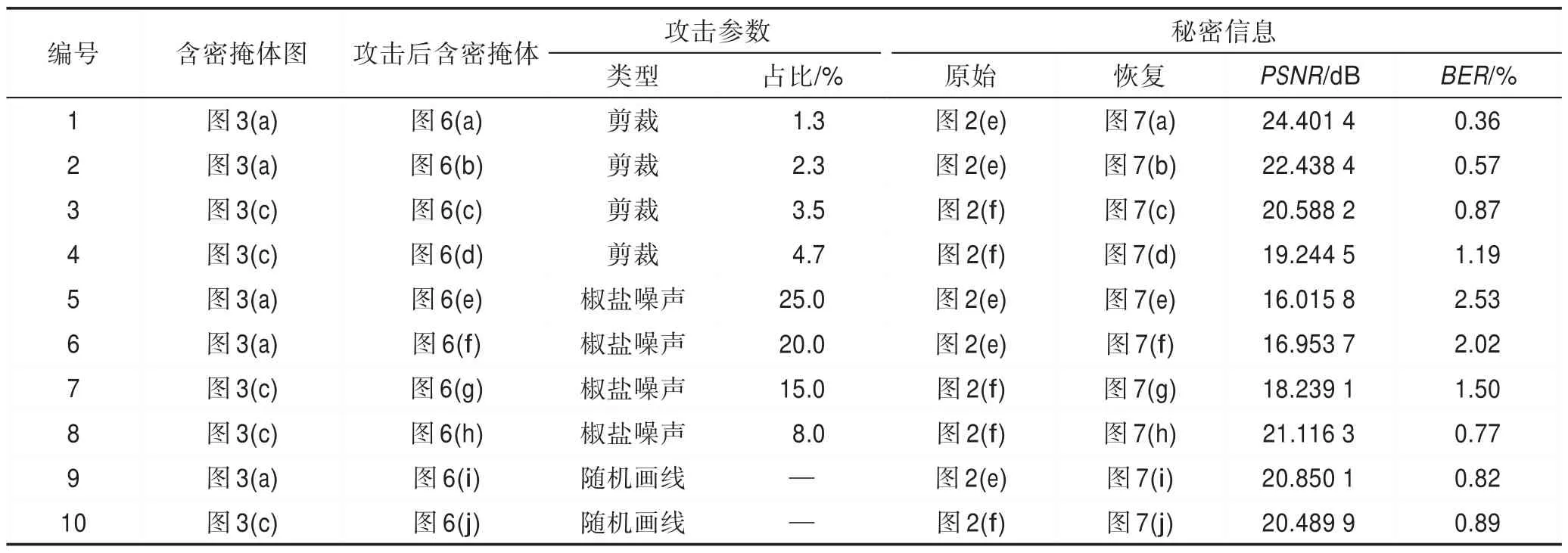
Table 5 Attack experiment parameters表5 抗攻击实验参数

Fig.6 Attacked cover images in attack experiment图6 抗攻击实验中遭受攻击的含密掩体图

Fig.7 Recovered secret information in attack experiment图7 抗攻击实验中恢复的秘密信息

Fig.8 Recovered cover images图8 恢复的掩体图像

Table 6 Recovered cover images experiment parameters表6 掩体恢复实验参数

图8 给出了重构后的掩体图像，表6 给出了具体的实验参数。其中图8（a）、图8（b）所对应的嵌密容量为54 000 bit，图8（c）、图8（d）所对应的嵌密容量为30 000 bit。从表6 和图8 可看出，无论嵌密容量是54 000 bit 还是30 000 bit，本文所嵌入的秘密信息不会对含密掩体图的视觉质量造成任何影响，因此所提方法可等质量无损地将含密掩体图重构为原掩体图像。

4.5 二次聚类编码的有效性验证实验

为验证二次聚类编码的有效性，将算法5 和算法6 所涉及的二次聚类编码中的第一重聚类筛选算法剔除，然后和包含完整二次聚类编码的算法5 和算法6 的实验结果在同等攻击情况下进行对比。图9 给出了实验结果，图9（a1）～图9（d2）为占比2.3%的剪裁攻击后的含密掩体图；图9（e1）～图9（h2）为与之对应的提取的秘密信息；图9（i1）～图9（l2）为占比20%的噪声攻击后的含密掩体图（图9（i1）～图9（l2）的实际分辨率为2 048×2 048 像素，因此20%的噪声在图中无法显示出来）；图9（m1）～图9（p2）为与之对应的提取的秘密信息；图9（q1）～图9（t2）为随机画线攻击后的含密掩体图；图9（u1）～图9（x2）为与之对应的提取的秘密信息。其中，编号为1 的分组对应的图样为剔除第一重聚类的实验图像，编号为2 的分组对应的图样为完整二次聚类编码的实验图像。表7 给出了相关的实验参数，表8 给出了具体的实验数据。

Table 7 Parameters in validity of quadratic clustering coding experiment表7 二次聚类编码的有效性验证实验参数

从图9 可看出，使用完整二次聚类编码的编号为2 的所有分组恢复结果明显好于剔除第一重聚类筛选算法的编号为1 的所有分组，这些也可被表8 中的最好结果（粗体数据）所证实，并且随着样本小块数量的增加，完整二次聚类编码相对于剔除第一重聚类筛选算法的优势越来越明显，表现为表8 剪裁、加噪和随机划线对应的4 个分组随着样本小块数量的增加，PSNR和EBR的差异都在增加。原因是随着样本小块数量的增加，产生相似样本块的可能性增大，完整二次聚类编码的第一重聚类筛选算法可有效地剔除相似样本小块的影响，降低误判概率，从而在同等攻击程度上，具备更强的抗攻击能力。

Fig.9 Images in validity of quadratic clustering coding experiment图9 二次聚类编码的有效性验证实验图像

4.6 与传统方法的对比

4.6.1 拼接痕迹对比

图10 为传统裂缝拼接法[10-11]和最小误差纹理合成法[12]的实验结果，其中图10（a）、图10（b）为分辨率为256×144 像素的样例图像，重叠区域大小为256×32；图10（c）为传统裂缝拼接的实验结果，图10（e）为最小误差纹理合成的实验结果。图10（d）和图10（f）分别对图10（c）和图10（e）拼接的重叠区域和误差线进行了标记。注：为使拼接痕迹更为明显，实验中增大了拼接重叠区域的大小。图11 给出了本文方法生成的二值样本块直接拼接的实验结果，其中图11（a）和图11（b）是分辨率为256×128 像素的二值噪点样本块，图11（c）是图11（a）和图11（b）进行直接拼接的结果。

从图10 和图11 的实验结果可以看出，传统裂缝拼接和最小误差纹理合成都有明显的拼接痕迹，本文方法因为使用了二值噪点图作为样本小块，因此即使不借助任何拼接算法也能有效地避免拼接痕迹。

4.6.2 嵌密容量对比

传统基于搜索的无载体信息隐藏主要通过检索数据库中包含指定秘密矢量的自然无修改载体来传递秘密信息。由于自然载体图像和文本对与之不相关的秘密信息的表达能力十分有限，导致这类方法单载体嵌密容量极低，涉及大量载体在信道中密集传输，从而容易引起怀疑和攻击，导致传输的秘密信息遭受破坏。

Table 8 Results in validity of quadratic clustering coding experiment表8 二次聚类编码有效性验证实验结果

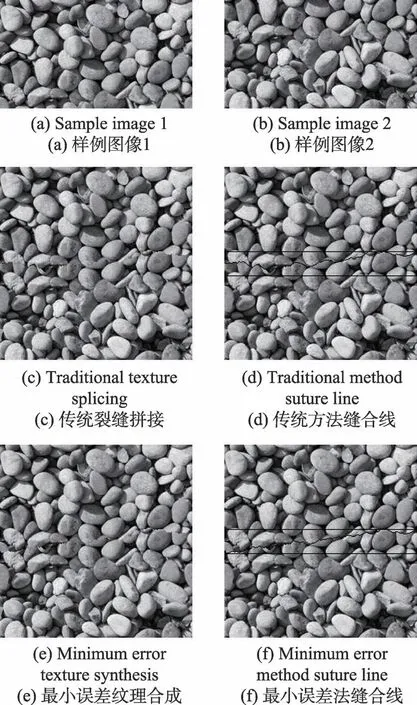
Fig.10 Traditional image synthesis and minimum error texture synthesis图10 传统图像合成和最小误差纹理合成

Fig.11 Spliced result of proposed method图11 本文方法的拼接结果

文献[5]将数据库中每张图像划分为9 个相等的图像块，通过均值比较的方式将一张图像映射为8 bit信息；文献[6]依据图像的SIFT（scale invariant feature transform）特征并结合图像数据集的K均值聚类以及BOF（bag of features）特征来产生特征向量并将其映射为8 bit 信息。文献[5-6]均通过最终映射的8 bit 信息将图像集划分为256 个类别，嵌密容量均为8 bit/图像。文献[7]构建的数据库更为庞大，通过K均值聚类建立图像局部分块特征和10 000 个视觉词汇之间的对应关系表达秘密信息，其嵌密容量仅为1.57 和1.86 中文字符/图像。

因此搜索式无载体信息隐藏的单载体嵌密容量极低。

本文所提方法通过编码样本小块来隐藏秘密信息，每个编码样本小块代表1 bit 秘密信息，样本小块的分辨率仅为8×8 像素。由于本文方法所生成的含密掩体图是将原始掩体图的每个像素点扩展为8×8分辨率的小块而生成的，因此本文方法的单载体嵌密容量与原始掩体图像大小有关；以4.1 节正确性验证实验为例，嵌密容量为65 536 bit/图像。

4.6.3 掩体视觉质量对比

图12 给出了文献[17]基于马赛克拼图的信息隐藏的含密掩体图，其中图12（a）、图12（b）是含密掩体图，图12（c）、图12（d）是与之对应的局部放大图。从图12 可看出，文献[17]马赛克之间存在着固有的拼接痕迹且含密掩体图上存在着大量的突兀点，导致文献[17]含密掩体整体视觉质量较差。

从图3 和图8 可看出，本文含密掩体视觉质量则整体较好，且本文所提策略在嵌密过程中始终选择与掩体放置位置最接近的编码样本小块，因此放置的秘密信息不会对含密掩体的视觉质量产生任何影响，含密掩体可等质量地恢复为原始掩体。

Fig.12 Experimental results of Ref.[17]图12 文献[17]的实验结果

4.6.4 性能综合对比

以下将本文策略同传统修改式信息隐藏[1-4]、搜索式无载体信息隐藏[5-7]、纹理生成式信息隐藏[8-12]和马赛克拼图式信息隐藏[13-17]进行综合性能对比。从表9 可看出本文算法具有较好的性能。

Table 9 Comparison with traditional methods表9 与传统方法的对比

5 结束语

为克服传统修改式信息隐藏、搜索式无载体信息隐藏、纹理生成式信息隐藏和马赛克拼图式信息隐藏存在的缺陷，提出了结合二次聚类编码的生成式可逆信息隐藏方法。将随机产生的不同灰度阶的黑色噪点图作为候选样本小块，经由二次聚类编码滤除不同灰度阶的相似样本小块，并进一步筛选出同一灰度阶的编码样本小块用于二值秘密信息的编码表示。所提方法通过生成的随机二值参考图结合随机嵌密位置来放置不同灰度阶的编码样本小块以编码秘密信息。理论和实验表明，所提方法可生成视觉质量良好的有意义图像，不会产生任何拼接痕迹，也不涉及任何修改式嵌入，具有良好的抗攻击能力，可抵御不同程度的剪裁攻击、椒盐噪声攻击以及随机画线攻击；另外，所提方法无论秘密信息如何嵌入，含密掩体均可等质量地无损恢复为原始掩体图像，且嵌入和提取过程完全依赖于用户密钥，具有较高的安全性。本文方法尽管通过随机黑色噪点小块避免了拼接痕迹，但所生成的含密掩体通过空间分辨率来表达灰度分辨率，会带来像素的膨胀，如何有效地解决该问题，还需要进一步的研究。