HSI空间上高噪声彩色图像去噪方法研究*

杨 培，高雷阜，訾玲玲

1.辽宁工程技术大学 运筹与优化研究院，辽宁 阜新 123000

2.辽宁工程技术大学 电子与信息工程学院，辽宁 葫芦岛 125105

1 引言

图像在成像、传输等过程中因各种因素会出现噪声点，图像噪声降低了图像质量，模糊了图像内容，使得图像的可靠性降低，进而影响到后续图像信息的处理。图像去噪将噪声和图像的真实内容分离开，突出图像信息特征并去除噪声，达到提高图像清晰程度、优化图像质量的目的。

随着成像设备的迅速发展以及人眼对色彩的敏感反应，彩色图像越来越普遍地出现在不同领域。彩色图像包含比一般图像更多的信息，受噪声污染的彩色图像对后期的图像处理会带来很多麻烦，对其进行去噪，成为了一个不可忽视的问题。国内外很多学者对彩色图像的去噪，不断进行着探索，He 等[1]在HSI（hue-saturation-intensity）空间中，将色调和饱和度相结合实现全变差扩散去噪，又基于矢量扩散流对亮度分量进行去噪，但算法复杂度高，对较高噪声的去除效果欠佳。Andreas 等[2]在HSI 空间中使用色度中值滤波器较好地保持颜色特性，但没有对I 分量进行处理。张云强等[3]通过搜索色度中值消除H和S 中的噪声，采用贝叶斯多阈值对I 分量噪声进行消除。Ono 等[4]提出矢量全变分先验方法去除彩色图像的噪声，以分离的方式测量亮度分量和色度分量的离散梯度，减少了不均匀色彩效果，减轻了色彩的失真现象。贾迪等[5]构造RGB（red-green-blue）空间下的梯度矢量计算方法进行彩色图像去噪。Moreno等[6]使用R、G、B 各通道的梯度信息构造耦合的交叉项对彩色图像去噪。芦碧波等[7]在RGB 色彩空间中提出基于黎曼几何驱动的彩色图像去噪方法，使图像的边缘得到更好的保持。Radlak 等[8]利用卷积神经网络通过训练来学习残差图像，解决彩色图像脉冲降噪问题。在对彩色图像去除噪声时，上述文献中均是投影到不同色彩空间中进行处理，实现了不同的效果，其中较频繁使用的色彩空间是RGB 空间，但该空间中R、G、B 三个分量不仅表示色度也表示亮度，有较强的耦合性，任意分量的改变都会改变总体颜色信息。相比于其他色彩空间，HSI 被认为是更接近人类视觉感知的色彩空间，该空间中H 与S 分量与人感受颜色的方式是紧密相连的，很适合彩色特性的检测与分析，这两个分量相互关联，共同构成图像的色彩信息。亮度分量I 与色彩信息无关，通常按照灰度值来处理，只是将人类视觉“感觉”的重要信息传递到图像上，该分量与H、S 分量相互独立，故而将亮度与彩色图像中携带的色彩信息剥离后再进行处理，互相之间是不影响的。因此本文选择HSI 空间进行彩色图像的去噪。

图像去除噪声的处理中，基于多尺度几何分析（multi-scale geometric analysis，MGA）方法以其独特的几何正则性，实现了图像最佳稀疏表示，很多学者采用MGA 方法对图像进行分析，区分出原始图像与噪声的特征，进而达到去除噪声的目的。贾建等[9]在非下采样轮廓波变换（non-subsampled contourlet transform，NSCT）域中，根据正态拟高斯模型构建的阈值函数进行图像去噪。刘帅奇等[10]在剪切波变换和稀疏去噪的基础上，采用共轭梯度迭代硬阈值对图像进行去噪。王智文等[11]通过最小化残差来调整模型参数，根据分形小波变换的自相似性对各部分进行统计去噪，较好地保留了图像的精细结构。王相海等[12]提出隐马尔可夫树模型进行图像去噪，有效保留了原图像的几何信息。Ji 等[13]在剪切域进行贝叶斯迭代估计稀疏系数，对不同尺度的系数通过协作聚合对图像进行去噪。Jiao[14]通过轮廓波变换将图像进行多尺度分解，根据灰色关联度来区分噪声和边缘信息，提高了图像的均衡性。这些文献通过不同的方式实现了图像去噪，说明了采用MGA 方法进行图像去除噪声的可行性和有效性。一般而言，基于MGA 的去噪方法先将图像转换到多尺度变换域，然后采用阈值方法对不同尺度和方向的系数进行联合或单一去噪，最后对去除噪声后的图像进行相应的重构。在不同的多尺度变换比较研究中，非下采样剪切波变换（non-subsample shearlet transform，NSST）[15]以其完备的数学理论、敏感的方向性、紧支撑的离散多尺度性等独特优点，能更优地表达出图像的细节特征，因而本文在多尺度变换中采用NSST 变换以期得到更好的去噪效果。

NSST 由非下采样的拉普拉斯金字塔变换（nonsampled Laplacian pyramid，NSLP）和剪切波滤波器（shearlet filter，SF）实现，先通过NSLP 进行多尺度分解，再通过SF 实现方向局部化，通过N级分解后，噪声图像最终析离出1 个低频子图和N个大小相同但方向尺度不同的高频子图，相应的噪声和细节信息多留在高频子图中，低频子图中包含了大量能量但噪声较少。本文采用常规的稀疏去噪方法对含有较少噪声信息的低频子图进行处理[16]，力求进一步提高去除噪声后图像的质量。对于包含了图像各方向的边缘等细节信息的高频子图，本文尝试着在高频中分析噪声特点，将噪声和图像的有效边缘信息区分开来，再从中剔除需要去掉的噪声点，达到提高图像质量的目的。

基于以上分析，本文构建了一种彩色图像的去除噪声方法，首先对噪声图像进行HSI 变换，然后对于色调H 和饱和度S 构造的二维向量空间，提出极坐标系下的距离阈值去噪方法。同时对亮度I 进行NSST 变换，对含噪声点较少的低频子图，采用稀疏字典学习进行去噪；对噪声点集聚的高频子图，提出自适应梯度阈值去噪方法。最后，进行NSST 逆变换得到去除噪声后的分量I，再联合去噪后的H、S 分量进行HSI 逆变换得到最终彩色图像。通过实验的主客观分析验证本文方法的有效性。

2 HSI空间上彩色图像去噪方法

2.1 极坐标中距离阈值去噪

HSI 空间中，色调H 与饱和度S 均表示颜色信息，H 分量通常以角度度量，S 通常表示离I 轴的远近程度，人类感知的色彩是这两个分量的合成。文献[2]中建立的色度模型保持了图像的色彩特性。文献[3]中基于这种模型，提出色度中值滤波器去除色彩中的噪声，虽然保真色彩，但滤掉的噪声点很少。本文在色度模型的基础上，在保持颜色不失真的情况下，构造了平均最小距离阈值，尽可能滤掉更多的噪声点，提出了极坐标中距离阈值去噪（distance threshold denoising in polar coordinates，DST），对H 和S 去除噪声，具体处理过程如下：

步骤1分块预处理。将彩色图像进行HSI 分解后，对饱和度分量矩阵S和色调分量矩阵H进行相同的分块处理，块大小为r×c。将两个分量矩阵中任意相同位置的块记为块矩阵s、块矩阵h，并寻找块中像素点数值的最小值，分别记为smin和hmin。

步骤2极坐标系下块中颜色量的定义。设块中任一点（m，n） 处表示颜色的量为Cmn，且满足m=1，2，…，r；n=1，2，…，c，若smn、hmn分别表示点（m，n）处的饱和度值和色调值，则对于块矩阵s和h，有smn=s（m，n），hmn=h（m，n），那么在极坐标系下可定义：

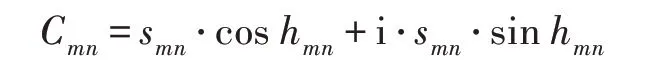
其中，i 为虚数单位。这说明用块矩阵s和h联合定义的块中每一个表示颜色的量都是个复数，点（i，j）处的颜色量Cij也是个复数。

步骤3距离阈值的设置。块中的点（i，j）与其他任一点（m，n）的距离可由下式计算。

其中，在块矩阵s和h中，sij、hij是点（i，j）处的饱和度值和色调值，即sij=s（i，j），hij=h（i，j）；smn、hmn是点（m，n）处的饱和度值和色调值，即smn=s（m，n），hmn=h（m，n）。

当m=1，2，…，r；n=1，2，…，c时，对于固定点（i，j），所有的可以构成像素点（i，j）与块中其他任意像素点的距离矩阵Dij∈Rr×c，设Dij中非0 的最小值为dij，则块中每一个点对应一个非0 的最小距离值。所有最小距离值的平均值可通过下式计算得到。

步骤4噪声的消除。若在块中点（i，j）处有dij＞d，则说明同等条件下该像素点与周围其他像素点的差距较大，相似性太小，在此处产生了突变。根据噪声点的突变型，可判断该点是噪声点，需要去除掉。设块中去除噪声后的饱和度和色调块矩阵分别为ends和endh，具体处理过程如下所示。

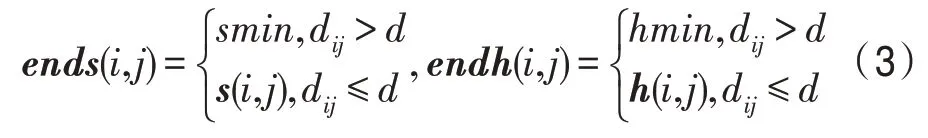
其中，i=1，2，…，r；j=1，2，…，c。对ends和endh进行分块逆变换，得到最终的去除噪声后的饱和度矩阵endS和色调矩阵endH。

2.2 自适应梯度阈值去噪

图像经NSST 分解后的高频子图中含有图像中的细节信息，噪声在图像中归属于细节信息。分解的尺度越大，留在低频子图中的细节信息越少，高频中的细节信息量就越大，留在高频中的噪声也就越多。为了区分出含噪声图像中噪声和边缘等细节信息，以灰度图像lena 为例进行图像分析。图1 中从左至右依次是原始图像、所加噪声的图像、含噪声图像。

Fig.1 Original sample image of image analysis图1 图像分析原始示例图

为了能更清晰展现出高频中噪声的特点，需要将更多的噪声留在高频中，因而NSST 中的分解尺度设置为4，每个尺度的分解方向数为4、4、8、8。图2为含噪声的lena 图像经NSST 分解后得到的高频子图，这些高频子图在图像中显示为黑色区域中嵌入白色或者灰色细节。为了能更好显示这些图像，对这些高频子图进行取反操作并显示。通过图2 很容易看到，这些子图中含有噪声的多少是各不相同的。在第1、2 个尺度中含有大量的边缘细节信息，噪声信息较少。而在第3、4 个尺度中含有的噪声信息较多，第3 个尺度中噪声信息和边缘等细节信息共存，大约有4 个方向含有较明显的边缘细节信息，第4个尺度中的8 个方向上几乎没发现边缘细节信息，布满了噪声信息。

在图像处理中，图像的梯度可以提取出图像的边缘等细节信息。梯度值较大的像素表明其处于图像边缘，梯度值的变化表示图像的内容有所改变。在高频子图中，边缘信息虽会导致图像的梯度值较高，但其变化一般是连续的且有规律性，与噪声相比变化还是较平缓，过于频繁剧烈的梯度变化一般都是由噪声引起的。为了将噪声同其他细节信息分离开来，本文从梯度的角度，对以上高频子图进行数值分析。首先对以上的高频子图求其各自的梯度系数矩阵，再对每个梯度系数矩阵求其平均值，计算所得具体数值如表1 所示。对表1 中所有值再求其平均，可得到最终的平均值为0.008 497，与表中各梯度平均值相比较，发现第1、2 尺度的任一方向平均值都比这个平均值小，说明该尺度中每一方向的子图总体变化平稳，噪声点较少。而第3、4 尺度的数值都比这个平均值大，说明在第3、4 尺度中含有更多的噪声，每个子图中整体突变频繁，噪声点较多，恰好与图2的观察结果一致。而第2、3 尺度中噪声信息和边缘信息共存，这就需要对具体的像素点进行单独处理，将其区分开来。

Fig.2 High frequency subgraph of noise lena image after NSST decomposition图2 含噪lena 图像经NSST 分解后的高频子图

基于以上分析，本文在高频子图的去噪处理中提出了一种自适应梯度阈值去噪（adaptive gradient threshold denoising，AGT），具体处理过程如下所示。设亮度I 的第k个尺度、第s个方向的高频子图为Ik，s∈RM×N。

Table 1 Average value of gradient coefficient matrix of high frequency subgraphs in different scales and directions表1 不同尺度不同方向的高频子图梯度系数矩阵的平均值

步骤1高频子图梯度系数矩阵的构建。

设高频子图Ik，s的梯度系数矩阵为gIk，s，则gIk，s中（i，j）点的数值为该点处水平方向与竖直方向梯度平方和均值的开方，其计算公式如下所示。

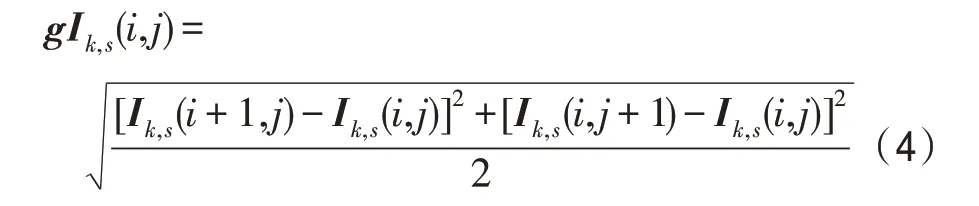
其中，i=1，2，…，M；j=1，2，…，N。

步骤2自适应梯度阈值中相关参数的求解。

设gIk，s中所有数值的平均值为gmk，s，则有：

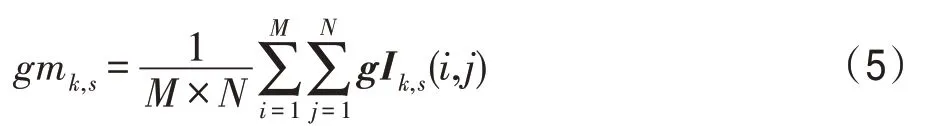
对所有不同尺度及方向的均值gmk，s再求平均，设得到总体平均值为gm，则计算公式为：

其中，K、S分别为分解尺度数和最大方向数。

步骤3 权值的构造及高频去噪规则的建立。

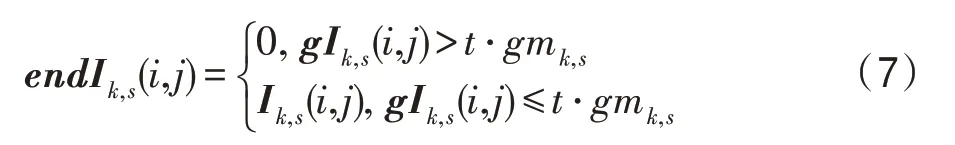
Fig.3 Process diagram of color image denoising in HSI space图3 HSI空间上彩色图像去噪过程图

2.3 去噪过程

本文对彩色图像进行去噪的过程如图3 所示。将彩色图像投影到HSI空间后，对H、S 分量进行极坐标中距离阈值DST 去噪；对NSST 变换后I 分量的高频子图进行自适应梯度阈值AGT 去噪；对低频子图采用稀疏去噪，最后经相应的逆变换得到最终去除噪声后的彩色图像。具体过程如下所示。

输入：含噪声的彩色图像。

输出：去噪后的彩色图像。

步骤1对含噪声的彩色图像进行HSI 变换得到三个分量矩阵H、S、I。

步骤2色调H、饱和度S 去噪。

对分量矩阵H和S，先进行图像分块预处理，然后在极坐标系下对块中颜色量进行定义，再由式（1）、式（2）计算距离最小值dij和阈值d，最后根据式（3）进行去噪，进而得到最终去除噪声后的饱和度分量矩阵endS和色调分量矩阵endH。

步骤3亮度I去噪。

对分量矩阵I进行NSST 分解，得到低频分量Ilow和一系列高频分量Ik，s。

高频分量Ik，s去噪：先根据式（4）求得梯度系数矩阵gIk，s，然后根据式（5）得到每个高频子图的gIk，s的平均值，再由式（6）求得总体平均值gm，最后构造权值并根据式（7）判断出噪声点，进而得到噪声去除后的endIk，s。

低频分量Ilow去噪：对低频分量的噪声采用稀疏优化方法进行去噪，其中的字典学习采用ODL[16]（online dictionary learning）算法进行训练，稀疏分解选用LARs[17]（least angle regression）算法，重构后得到最终低频噪声去除后的endIlow。

步骤4对低频endIlow和高频endIk，s进行NSST逆变换得到去除噪声后的亮度分量endI，再对endS、endH和endI进行HSI 逆变换得到最终去噪后的彩色图像。

3 实验结果与分析

3.1 实验设计

实验主要分两部分进行：一是检验本文构建的灰度图像去噪方法的有效性，即是对亮度信息I 采取的噪声去除方法可行性的验证，分析了自适应梯度阈值去噪（AGT）的效果；二是在受高噪声污染的彩色图像中，检验本文提出HSI 空间下彩色图像去噪方法的有效性，并分析极坐标中距离阈值去噪（DST）方法中彩色部分的去噪保真效果。

图像去除噪声的过程采用Matlab R2016a 编程实现仿真模拟，运行环境Intel®Core™i7-10510U CPU，12 GB 内存，操作系统Windows 10。在条件一致的情况下，稀疏去噪中字典学习均采用ODL 算法，滑动窗口大小为8×8，步长为8，迭代次数为10。小波变换时采用小波基函数db4 进行处理，分解层次数为4。NSCT 变换时金字塔滤波器组选用“maxflat”，方向滤波器组采用“dmaxflat7”，分解尺度采用自适应于图像尺寸的方式，分解方向设置为8。NSST 变换中分解尺度为4，方向分解数为[4，4，8，8]，采用“maxflat”作为分解滤波器，采用“shear”滤波器作为方向滤波器。

图像去噪效果可以通过主观和客观分别进行分析。首先需要从视觉上对图像进行认同，在主观效果近似时通过客观标准进行检验。实验选取的定量评价指标分别是峰值信噪比（peak signal to noise ratio，PSNR）、均方根误差（root mean squared error，RMSE）、结构相似度（structural similarity，SSIM）、相对熵（relative entropy，RE），其中PSNR 是最普遍和使用最为广泛的一种图像客观评价指标，它是基于误差敏感的图像质量评价。RMSE 表示两幅图像间的差异程度，取值越大，说明去噪后的图像与干净图像差异越大，去噪效果越差。SSIM 通过计算图像亮度、对比度、结构信息等特征量来评价两幅图像的差异，评价结果与人眼感知具有一致性。结构相似度越大，表示去噪后的图像与干净图像越接近，去噪效果越好。RE用于描述两幅图像像素值分布的信息差异，其值越小，说明两幅图像对应位置像素数值的差异越小。以上这些指标中，PSNR 与SSIM 数值越大越好，RMSE和RE 的数值越小越好，具体计算公式见文献[18]。

3.2 构建灰度图像去噪方法的有效性

这部分实验的测试图像为标准lena 图（512×512）和生活中随机采集的chutty 图（512×512），对两幅图像分别加高斯白噪声作为原始噪声图像。比较方法分别为：（1）Wave-HT（wave-hard threshold to denoise），小波阈值去噪方法[19]；（2）DLtN（dictionary learning to denoise），基于字典ODL 的稀疏去噪方法；（3）NSSTNIG（NSST-normal inverse Gauss to denoise），基于NSST 的图像去噪方法[20]；（4）NSCT-AGT，本文的AGT 与NSCT 相结合的去噪方法；（5）Curve-AGT，AGT 与曲波变换相结合的去噪方法；（6）NSST-AGT，AGT 与NSST 相结合的去噪方法；其中方法（4）至（6）中的低频均采用稀疏去噪，而方法（6）NSST-AGT 也是本文中对亮度信息I采取的噪声去除方法。

图4、图5 展示了在噪声标准差σ=60 的高噪声环境下，各种方法对灰度lena 图和chutty 图的噪声去除效果。通过观察，发现图4 中DLtN 方法去除噪声后图像清晰度欠佳，NSST-NIG 中人物下巴与肩膀相接的边缘处轮廓较模糊，帽檐处较平滑。Wave-HT方法的图像虽有较好的轮廓，但视觉上图中还有噪声存在。Curve-AGT 去除噪声后的效果有带状条纹，说明曲波变换在高噪声时对lena 图去噪不占优势。本文的AGT 与多尺度结合的两种方法NSCT-AGT、NSST-AGT 的去除噪声效果与其他方法相比，在噪声标准差较高时效果较好，其中NSST-AGT 方法的视觉清晰度更好。

Fig.4 Visual comparison of denoising effect in gray lena image图4 灰度lena 图去噪效果的视觉比较

Fig.5 Visual comparison of denoising effect in gray chutty image图5 灰度chutty 图去噪效果的视觉比较

图5 展示了生活中随机拍摄的口香糖瓶体图像去除噪声效果。通过视觉观察，明显看到Wave-HT和DLtN 去除噪声后图中依然有噪声点存在。Curve-AGT 中出现条纹状线条，NSST-NIG 中字体较模糊。通过图中最下方字体相比较，NSST-AGT 比NSCTAGT 方法的字体更加清晰。由主观视觉效果可知，本文方法在高噪声情况下对亮度信息I采取的NSSTAGT 去除噪声方法明显占优。

表2 和表3 显示了两幅图像去除噪声所采用的各方法运行时间及四种客观评价指标的数据，最优值加粗标注。在时间消耗上，Wave-HT 方法运行时间最短，因为其中的小波分解采用了下采样，数据量处理得较少，时间较短。DLtN 方法去除噪声消耗时间最长，因噪声导致图像结构性降低，使得稀疏表示时稀疏性较弱，数据量增加。此外，在字典学习中采用的滑窗模型也使得数据量增大，造成了DLtN 总体运行时间长。余下的四种多尺度去噪方法中，本文灰度图像去除噪声采用的NSST-AGT 方法运行时间比其他的三个方法稍高，相比于这四种方法的时间平均值来说，上浮幅度在10%左右，时间上并不占优。

在去噪效果的其他四种客观指标上，当噪声标准差为60 时，表2（lena 图）中，NSST-AGT 在PSNR、RMSE 中占有最优值。噪声图像的SSIM 值最高，这是因为受高噪声污染的图像结构已经被破坏得较严重，在此基础上进行去噪，势必会对结构造成更多的破坏，使得这些方法的SSIM 值较噪声图像低，但本文方法相比于其他方法依旧有优势。在RE 值比较中，NSST-AGT 略逊于噪声图像和NSCT-AGT 方法。在表3（chutty 图）中NSST-AGT 方法的四种客观指标明显占优，通过以上这些数值说明了本文构建的灰度图像去噪方法的有效性。

Table 2 Comparison of objective indexes of lena image denoising effect（σ=60）表2 lena 图去噪效果客观指标比较（σ=60）

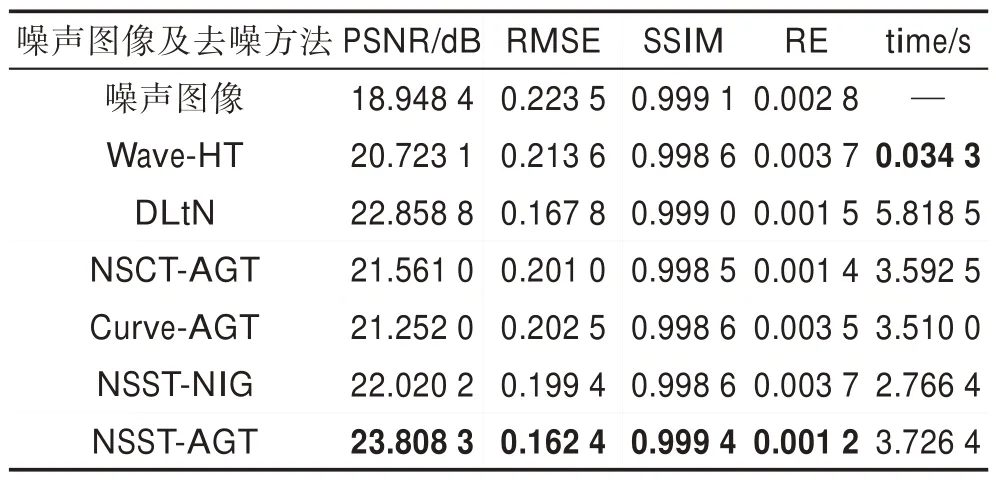
Table 3 Comparison of objective indexes of chutty image denoising effect（σ=60）表3 chutty 图去噪效果客观指标比较（σ=60）

图6、图7 分别展示了lena 图和chutty 图在不同噪声标准差σ下的各方法噪声去除效果的定量比较，为了尽可能减少实验误差，实验中的不同方法在不同噪声标准差下的数值均为50 次运行后的平均值。在PSNR、RMSE、SSIM、RE 四种指标的比较中，随着噪声标准差的增大，NSST-AGT 的噪声去除效果明显超过了其他方法。图6（c）SSIM、图6（d）RE 比较中，NSST-AGT 方法的数值指标与噪声图像相比稍差。这是因为当噪声标准差超过60 时，噪声过大，破坏了原图像的结构性，在背离真实图像时进行的噪声去除处理，计算所得的这两个数值指标较劣于噪声图像，但与其他方法相比仍然占据优势。

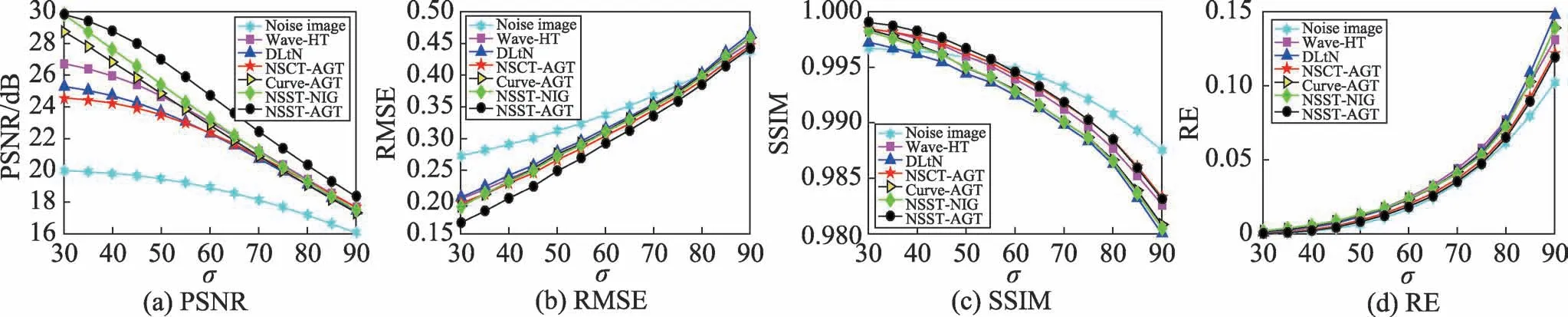
Fig.6 Quantitative analysis of denoising effect in gray lena image图6 灰度lena 图去噪效果的定量分析

Fig.7 Quantitative analysis of denoising effect in gray chutty image图7 灰度chutty 图去噪效果的定量分析

3.3 HSI空间下彩色图像去噪方法的有效性

这部分实验测试图像为标准彩色图像lena（512×512）、barbara（512×512）、house（256×256）以及生活中随机彩色图像child（512×512）、sweet（512×512）。对这些图像分别加高斯白噪声作为原始噪声图像。采用六种去除噪声的方法进行对比测试，分别为：（1）g-HSI，对H、S、I三个分量分别进行高斯滤波去噪；（2）DST-g，分量H、S 采用本文的DST 方法，对分量I 采用高斯滤波去噪；（3）c-HSI（chroma-HSI），文献[3]中的方法；（4）DST-AGT，分量H、S采用本文的DST方法，对分量I采用NSST分解得到高低频分量，低频分量不采取任何处理，高频分量采用本文的AGT方法；（5）DST-MC，分量H、S采用本文的DST方法，I分量经NSST变换后的分量用Monte-Carlo方法进行估计，再用阈值函数进行收缩去噪[21]；（6）DAD（DST-AGT-sparse denoising），本文提出的彩色图像去噪方法。

图8～图12 分别展示了五幅彩色图像在噪声值较高（σ=60）的情况下噪声去除后的视觉效果。DAD去除噪声后的效果较其他方法明显更好。g-HSI 和DST-g 对应的图中效果稍差，这与噪声去除过程中所采用高斯函数中标准差有关。标准差越大，平滑的作用域越宽，低通滤波效果越明显，图像也越平滑。但对于g-HSI 来说，它是对三个通道进行相同的滤波处理，标准差较大，去除噪声虽多，但由于没考虑色彩间的相关性，会出现色彩被破坏的现象。因而实验中高斯函数的标准差选取的是与所加噪声相关的自适应均方差。该参数值的选取虽然去除噪声较少，但保证了色彩不失真。

DST-g去除噪声的效果较g-HSI稍好。因为DSTg 中仅对I 分量进行了高斯滤波去噪，参数的大小对其部分影响。对H 和S 分量采用本文提出的极坐标中距离阈值DST 进行去噪，由此也说明了DST 在保持色彩不失真的情况下去除噪声效果的有效性。

c-HSI 色彩保持得很好，但在噪声值较大的情况下，也出现了带状条纹，这在house 图房屋边缘和child 图滑梯和孩子的周围表现比较明显，也使得画面整体显得不太清晰。sweet图糖果包装纸由于条纹状的影响，几乎看不清上面的字迹。

这五幅图中，DST-MC 方法存在着明显模糊现象，lena 的下巴处，barbara 的围巾和肩膀相接处等边缘明显不突出，child 中孩子的面部很模糊，sweet 中糖果上的字迹也是相当不清楚。

Fig.8 Visual comparison of denoising effect in color lena image图8 彩色lena 图去噪效果的视觉比较

Fig.9 Visual comparison of denoising effect in color barbara image图9 彩色barbara 图去噪效果的视觉比较

Fig.10 Visual comparison of denoising effect in color house image图10 彩色house图去噪效果的视觉比较

Fig.11 Visual comparison of denoising effect in color child image图11 彩色child 图去噪效果的视觉比较

Fig.12 Visual comparison of denoising effect in color sweet image图12 彩色sweet图去噪效果的视觉比较

DST-AGT 和DAD 噪声去除效果较好，从画面的整体色彩和视觉清晰度来说，更加接近原始图像。这两种方法的主观视觉效果区别不大，但通过表4去噪效果的客观评价可以看到，DAD 的四种指标结果均优于DST-AGT，说明低频中稀疏去噪对整体噪声去除的主观影响虽然不是很大，但客观效果依然存在。

表4 展示了五幅彩色图像去除噪声效果的客观评价指标对比，本文提出的DAD 方法在数值比较上明显占优，其中只有lena 图的SSIM 指标中稍低于噪声图像和g-HSI，这是因为高噪声环境下，图像结构被破坏得较严重，g-HSI 由于其参数设置较低，使得对图像破坏较小，结构相似度也就较大，但去除噪声较少。而DAD 在被破坏结构的图像上进行去噪，去除噪声越多，对图像的结构破坏性就容易变大，但与其他方法相比依然有优势。

图13～图17 这五幅图像为在不同的噪声标准差σ下，六种不同方法去除噪声的客观效果，图中数据均是50次运行后的平均值。在图13、图15的（c）SSIM比较时，DAD 分别在噪声标准差大于55 和75 时，数值结果逊于噪声图像，说明在结构性破坏比较严重时，本文方法也很难保持结构性的不变。但总体来看，无论是从视觉效果，还是不同噪声破坏下的数值比较中，DAD 都表现出了它较强的自适应性，去除噪声的效果更优。

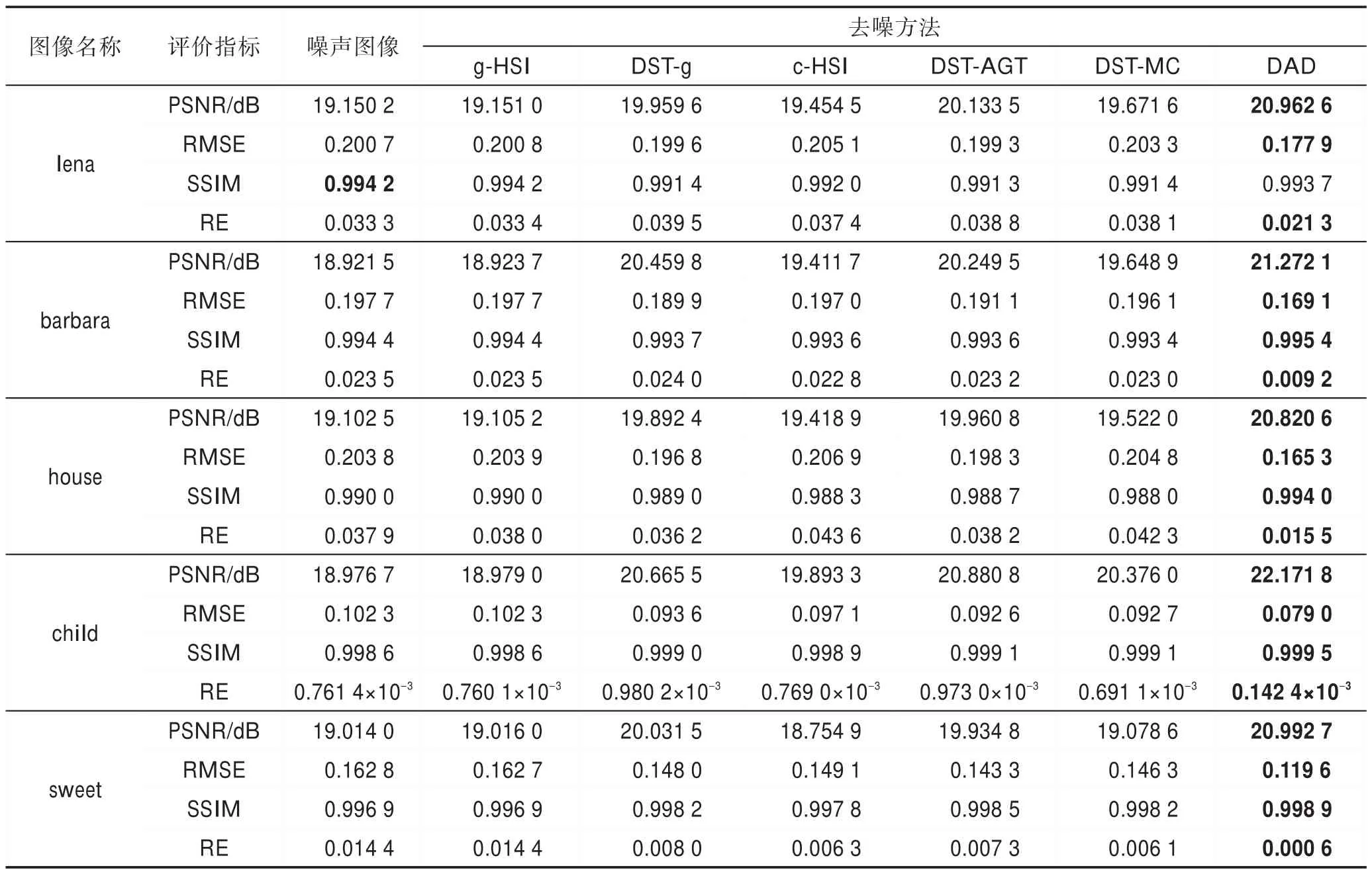
Table 4 Comparison of evaluation indexes of color image denoising effect（σ=60）表4 彩色图像去噪效果评价指标对比（σ=60）

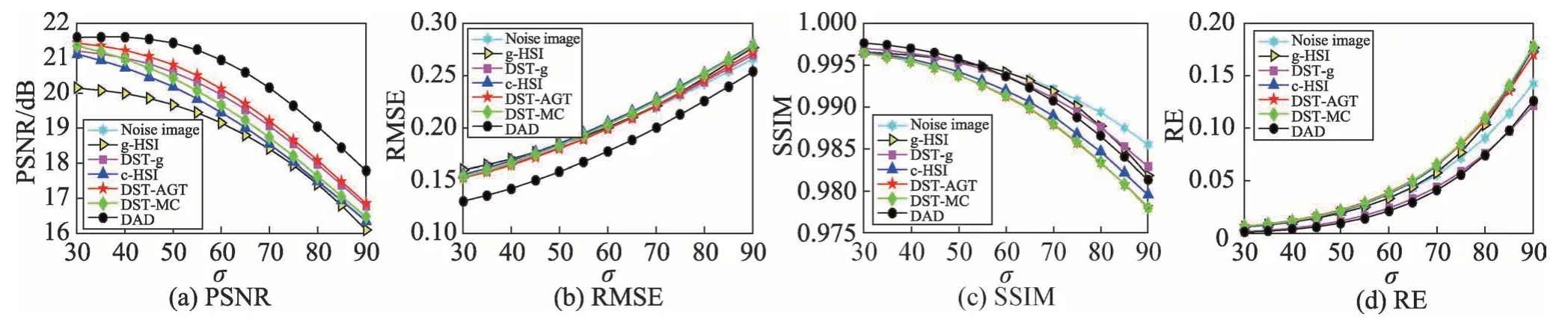
Fig.13 Quantitative analysis of denoising effect in color lena image图13 彩色lena 图去噪效果的定量分析

Fig.14 Quantitative analysis of denoising effect in color barbara image图14 彩色barbara 图去噪效果的定量分析

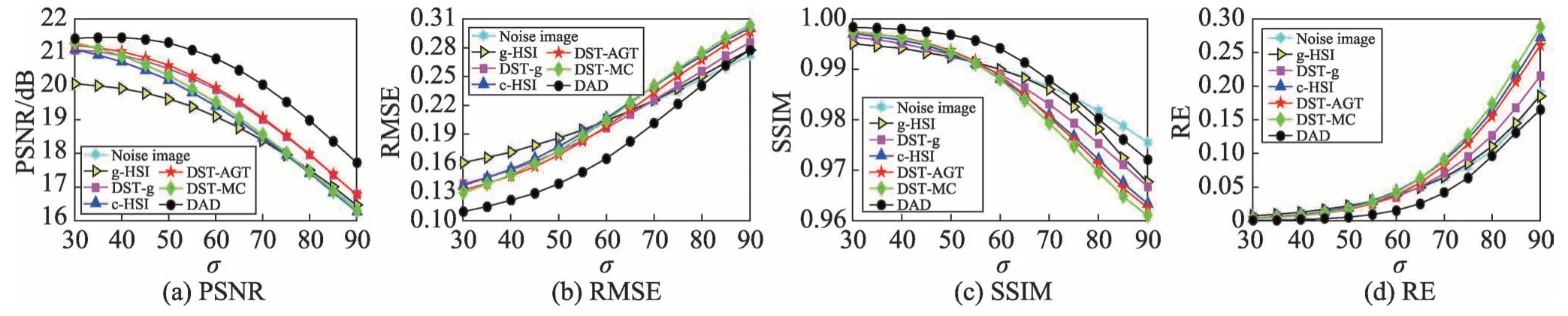
Fig.15 Quantitative analysis of denoising effect in color house image图15 彩色house图去噪效果的定量分析

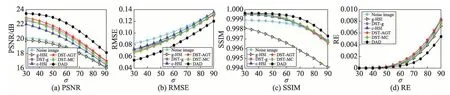
Fig.16 Quantitative analysis of denoising effect in color child image图16 彩色child 图去噪效果的定量分析

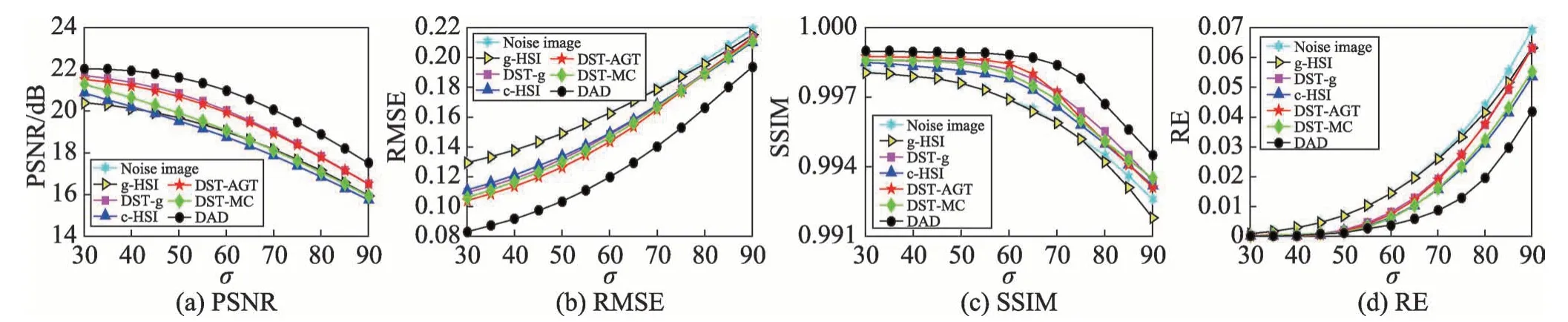
Fig.17 Quantitative analysis of denoising effect in color sweet image图17 彩色sweet图去噪效果的定量分析

图16 和图17 显示了两幅生活图像在不同噪声标准差σ下的各方法噪声去除效果的定量分析。在这两个图的（c）SSIM 比较中，g-HSI 方法结构相似度明显低于其他方法，结构性的破坏也导致了该对比方法在图16（a）PSNR 比较中和图17（b）RMSE 比较中数值结果较低。说明对三通道分量进行相同的噪声去除处理更容易破坏其结构，导致最终效果不佳，应结合不同分量相关性并根据其各自特点进行处理。在四种客观指标的比较中，无论是3 幅标准的彩色图像，还是随机采集的2 幅生活图像，本文方法DAD 在不同噪声标准差下去噪效果明显优于其他方法，从客观数值上说明了本文方法对高噪声彩色图像去除噪声的有效性。

3.4 时间复杂度分析

根据文中图3 的过程图可知，本文提出的去除噪声的方法DAD 包括三部分：DST、AGT 和稀疏去噪。对于DST 来说，去除噪声所消耗时间与主要块大小ksize有关，随着块尺寸变化呈平方增长，其时间复杂度的量级为O（ksize2）。AGT 部分主要是通过高频的梯度系数矩阵分辨噪声。为了提高运算速度，将单个高频子图的二维梯度矩阵计算分解为一维进行处理。若K、S分别为分解尺度数和最大方向数，n为图像一维尺寸大小，则AGT 时间复杂度应为O（KSn），又因为实际去除噪声时K，S≪n，所以其时间复杂度的量级为O（n）。由本文3.1 节稀疏去噪的实验条件分析可知，时间复杂度的量级为O（lbn）。实际实验中，块的大小ksize≪n，因此DAD 的时间复杂度的量级应为：

表5 展示了五幅彩色图像在不同噪声去除方法下的消耗时间，其中lena、barbara、child、sweet 四幅图的大小相同，数据量相同，在去除噪声时相同方法所消耗的时间相差不大。而house 图像大小是其他图像的1/4，数据量相应减少，去除噪声时耗费时间自然较其他图像少。不同方法消耗时间的比较中，g-HSI方法的三通道均用高斯滤波去噪，其时间复杂度随着滤波器尺寸呈现平方增长，实验中滤波器尺寸设置与DST 的块设置大小相同，故而其时间复杂度的量级为O（ksize2）。又因ksize≪n，所以实际实验中有O（ksize2）＜O（lbn）＜O（n），时间复杂度的量级明显较小，因此在表5 中g-HSI 的消耗时间最少。DST-g 方法在H 和S 上采用本文的DST 方法，虽然时间复杂度的量级与g-HSI 相同，但因增加了距离阈值计算过程，时间上较g-HSI 消耗多。后四种方法因采用了多尺度变换，使得时间花费上大于g-HSI 和DST-g。其中，DST-AGT 和DAD 由于在高频处理上时间消耗较多，使得整体去除噪声时间变长，两者之间，由于DAD 在低频中又加入了稀疏去噪处理，使得时间消耗更多。总之，DAD 方法与其他方法相比在时间上并不占优势。

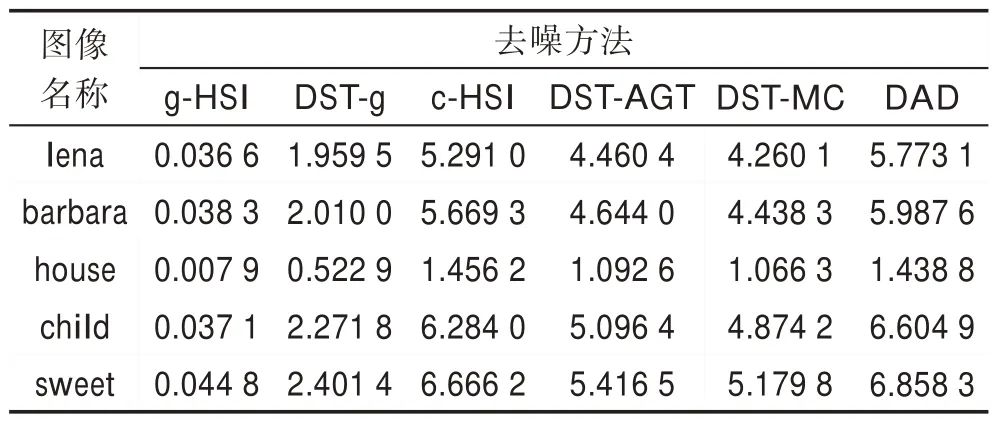
Table 5 Denoising time consumption表5 去噪时间消耗 s

4 结束语

本文对受噪声污染的彩色图像进行了去噪研究，构建了一种HSI 空间上对彩色图像进行去噪的方法。该方法将色调和饱和度投影到极坐标下构造距离阈值进行去噪，将亮度进行NSST 变换后，对其高频子图采用自适应梯度阈值进行去噪，对低频子图进行稀疏去噪。通过对本文方法的部分和整体的实验分析，无论是主观视觉还是客观指标上均达到了良好的效果，尤其对高噪声图像进行处理较其他去噪方法更有优势，此外还说明了HSI 空间上对彩色图像去除噪声是确实可行的。但本文方法未将时间消耗作为首要分析特征进行研究，期望在以后的研究中加以深化。