融入社会影响力的粒子群优化算法*

宋 威，华子彧

1.江南大学 人工智能与计算机学院，江苏 无锡 214122

2.江南大学 江苏省模式识别与计算智能工程实验室，江苏 无锡 214122

1 引言

受自然界动物群体行为的启发，Kennedy 和Eberhart 在1995 年提出了粒子群优化（particle swarm optimization，PSO）算法[1]。PSO 模拟鸟群觅食的行为来寻找解空间中的最优解。具体而言，每个具有位置矢量和速度矢量的粒子根据自身和种群中最优粒子的历史经验确定其下一步搜索轨迹。由于PSO 对优化问题的要求很少，只要能评估解决方案的质量，便可用于求解。在过去的20 年中，PSO 已引起了学术界的广泛关注。此外，在面对复杂优化问题时，PSO 的有效性也已得到验证[2]。目前，PSO 已广泛应用于电机设计[3]、路径优化[4]、应用检测[5]等多个领域。

PSO 的参数直接影响粒子的搜索过程，协调算法的全局“探勘”和局部“开发”能力。Shi 和Eberhart 最早利用惯性权重来更新粒子的速度[6]，并研究了不同惯性权重对种群的影响。在粒子的搜索过程中，他们对惯性权重进行线性递减控制，兼顾了搜索的广度和精度。此后，还逐渐发展出一系列的PSO 变体。邓志诚等人[7]提出具有动态子空间的随机单维变异策略和Pareto 速度分配策略，以解决全局最优粒子与普通粒子进化方向不一致问题。周蓉等人[8]提出一种基于灰狼优化的反向学习PSO，平衡了算法的全局和局部搜索能力。

除了PSO，目前还有多种基于群体的优化算法，比如遗传算法（genetic algorithm，GA）、差分进化（differential evolution，DE）和人工蜂群（artificial bee colony，ABC）等。GA 是一种模拟生物进化规律的仿生算法。根据基因的重组与进化，GA 将问题求解过程转化为基因的选择、交叉和变异三个过程，并利用多次世代遗传，以获取寻优结果[9]。然而，GA 的求解时间随种群规模呈指数级增加，往往造成过高的时间开销。与GA 类似，DE 也包括选择、交叉和变异操作，只是这些操作的具体定义与GA 有所区别[10]。然而，随着迭代次数的增加，DE 的种群规模会不断缩小，容易造成算法的停滞或过早地陷入局部最小点。ABC 利用跟随蜂贪婪选择雇佣蜂来进行局部搜索，同时利用侦查蜂的全局搜索特性跳出局部最优，拓展了搜索空间[11]。但是，由于从雇佣蜂到跟随蜂的角色频繁转换，会导致蜜蜂位置振荡，从而造成ABC的收敛速度过慢。相较而言，PSO 的求解时间与种群规模线性相关，求解速度较快。其种群规模在搜索过程中恒定，不存在算法停滞问题。而且，由于全局最优经验能在整个种群中得到快速分享，PSO 具有较快的收敛速度。

目前，在标准PSO 及其大多数变体中，全局最优粒子用于分享种群的最优经验。但是，在搜索过程中，当前全局最优粒子位置可能并非位于全局最优解附近，若仅考虑全局最优粒子对个体的影响，会导致种群学习对象单一，学习的多样性不足，使得算法易陷入局部最优。针对此问题，本文提出一种融入社会影响力的粒子群算法。具体而言，该算法设计了三种策略。首先，每个粒子将选择全局最优粒子和最优伙伴粒子作为其“社会学习”的对象，为每个粒子带来更丰富的有用知识。其次，引入引力系数分别描述各榜样带来的影响，在保证最优经验得到分享的同时，更多地是增强了种群学习的多样性。此外，每个粒子还在各维度上进一步向其最优伙伴粒子学习，实现从全局到局部的变尺度搜索，以提升算法的整体收敛能力。这三种策略从整体上有助于算法收敛到全局最优。并且通过广泛实验，其结果验证了PSOSI（PSO with social influence）的优越性。

2 粒子群算法

Shi和Eberhart于1998 年提出了带有惯性权重的标准PSO。该算法的各个粒子更新方式如下：

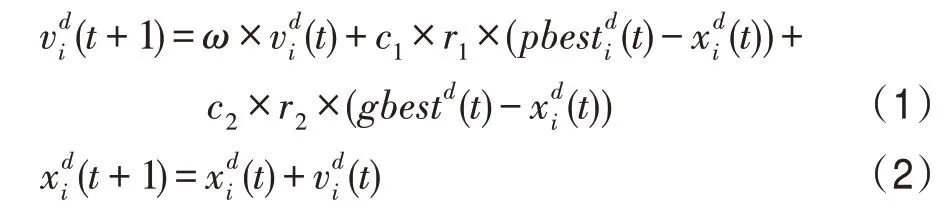
其中，t表示当前迭代次数，d代表维度，r1和r2是[0，1]范围内的随机数。pbesti是第i个粒子的历史最优位置，而gbest是种群历史最优位置。c1和c2代表学习因子。w是惯性权重，用于控制各粒子的上一代速度对当前速度的影响。目前通用的惯性权重控制方式是随着迭代次数的增加而线性减小：

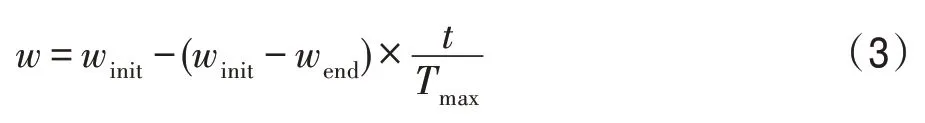
其中，winit为初始权重值，wend为最终权重值，Tmax代表最大迭代次数。

3 PSOSI算法

3.1 社会学习

在标准的PSO 中，每个粒子将全局最优粒子视为其“社会学习”的唯一榜样，但其学习的广度是远远不够的。类似于人类社会，向多个榜样学习是一种更为普遍的现象。并且，许多研究也已证明，向多个榜样学习的个体比仅从一个榜样学习的个体拥有更强的学习能力[12]。目前，多榜样学习已被应用于多个PSO 的变体。例如，Liang 等人[13]提出的全面学习PSO，各粒子选择不同粒子的最优历史信息作为其多个学习的榜样。

受人类社会的学习现象启发，每个粒子在其“社会学习”部分将向多个榜样学习。在PSOSI 中，各粒子选择全局最优粒子和最优伙伴粒子作为其“社会学习”的两个榜样。其中，最优伙伴粒子是每个粒子随机选择的两个伙伴中最好的个体。当粒子的适应值在连续若干代中没有提升时，粒子将重新随机地选择伙伴。

3.2 基于引力系数的社会学习

近年来，研究人员尝试利用引力模型从力学角度来解释各种社会现象[14]。研究表明，人们对他人的影响随着距离的增加而减弱。受此启发，本节基于社会学习来定义粒子向多个榜样学习的引力系数。

为了直观反映pbest和gbest对个体的影响，删除式（1）中独立随机变量r1和r2，学习因子c1和c2，以及惯性权重w。简化后的速度更新公式为：

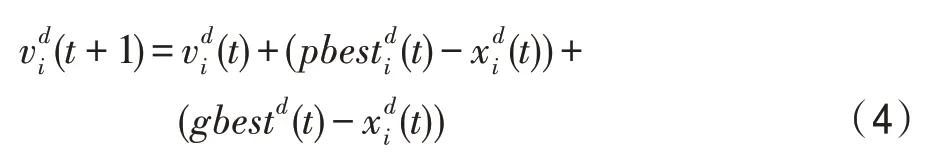
显然，粒子的速度仅受pbest和gbest影响。根据牛顿第一定律，即力是改变物体运动的唯一因素，式（4）中的两个向量，即可视为两个力，因为它们影响着粒子的运动。然而，这种力随着距离的增大而变大，导致种群多样性的降低。针对此问题，本文定义引力系数，从力学角度分别描述两个榜样对各粒子的影响。具体地，第i个粒子受全局最优粒子影响的引力系数ggri定义为：

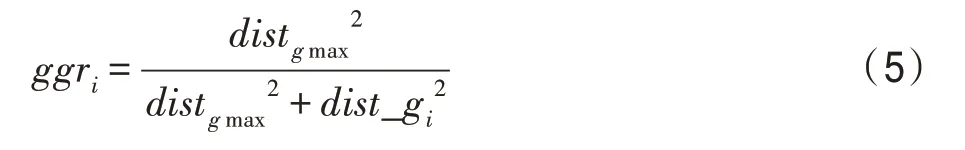
同时，第i个粒子受最优伙伴粒子影响的引力系数cgri定义为：

其中，distgmax代表全局最优粒子与其最远粒子的距离。由于全局最优粒子是当前种群中最优秀的个体，用于分享种群的最优经验，它影响着种群中的所有个体。dist_gi是第i个个体与全局最优粒子间的距离。distcmax，i代表第i个个体的最优伙伴粒子与该粒子最远伙伴间的距离。dist_ci代表第i个个体与其最优伙伴粒子间的距离。

由于distgmax是dist_gi的上界，基于式（5），ggri的取值范围为[0.5，1.0]。此外，由于个体i与其最优伙伴粒子分别选择各自的伙伴，即distcmax，i与dist_ci没有必然的联系，基于式（6），cgri的取值范围为（0，1）。在所提的基于引力系数的社会学习方式下，全局最优粒子负责向每个粒子传递当前的最优经验，将ggri设置为一个较大的值（0.5 ≤ggri≤1.0），以保证最优经验能得到分享。区别于全局最优粒子，最优伙伴粒子用于扩展种群学习的多样性，将cgri的取值范围设置为（0 ＜cgri＜1）。具体地，个体距离其最优伙伴粒子越近，cgri越大，因为距离的减小伴随着最优伙伴粒子影响力的增大。此外，与原始的PSO 相比，本文利用ggri一方面减弱了最优粒子的影响力，另一方面利用cgri来扩展多样性。因此，相对于原始的PSO，本文所提的基于引力系数的社会学习方式更多地是用于增强种群学习的多样性。通过引入引力系数ggri和cgri，粒子的速度更新公式定义为：

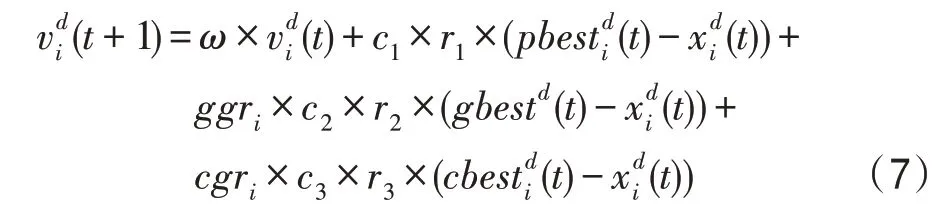
其中，cbesti是第i个粒子的最优伙伴粒子。类似于式（1），r1、r2、r3是[0，1]范围内的随机数，c1、c2、c3是学习因子。

3.3 基于最优伙伴的变尺度搜索

本文首先引入社会学习和引力系数两个策略来丰富种群学习的多样性，增加了算法收敛于全局最优解的可能性。为了进一步使算法趋于全局最优收敛，本文基于最优伙伴在各维度上的经验，进而利用提出的变尺度搜索策略，提高算法的整体收敛能力。具体地，各粒子根据式（7）和式（2）更新完速度与位置后，会进一步在各个维度上根据其与最优伙伴粒子的距离执行变尺度搜索：

其中，随机数r服从[-1，1] 的均匀分布。在算法初期，由于粒子在搜索空间中彼此相距较远，变尺度搜索将覆盖较大空间，增强算法的全局搜索能力。随着算法的迭代，当种群逐渐趋于收敛时，粒子间的距离相对较小，各粒子则在其自身周围进行较细致的局部搜索，提高了算法的收敛精度，使算法趋于全局最优收敛。同时，本文采用竞争性原理，该策略的结果当且仅当所产生子代位置的适应值更好时才保留。

3.4 时间复杂度分析

标准PSO 的时间耗费主要包括初始化、适应值评估，以及速度和位置的更新，由于它们的复杂度分别为O（mn）、O（mn）、O（2mn），其中m和n分别代表种群规模和解空间的维度，因此标准PSO 的时间复杂度为O（mn）。与之相比，改进的PSO 算法或多或少地引入了一些额外策略，但它们的时间复杂度大多仍与标准PSO 相同，比如Xia 等人[15]提出的XPSO（expanded PSO）需进行额外的遗忘学习；Tanweer 等人[16]提出的SRPSO（self-regulating PSO）引入自我感知策略来指导粒子的搜索过程，但XPSO 和SRPSO的时间复杂度仍为O（mn）[15-16]。区别于标准PSO，本文提出的PSOSI需要更新学习榜样。但是，榜样仅在粒子的适应值长时间没有改善时才会重选。重新选择学习榜样在最坏情况下的时间复杂度为O（m）。因此，PSOSI 在最坏情况下的复杂度仍然是O（mn），包括初始化的复杂度O（mn+m），评估的复杂度O（mn），更新的复杂度O（2mn+m），以及变尺度搜索的复杂度O（mn）。因此，PSOSI 的时间复杂度与标准PSO 算法保持相同。

3.5 算法流程

PSOSI 的流程图如图1 所示。相应地，PSOSI 的步骤如下：

输入：最大迭代次数Max，重选伙伴的阈值F。

输出：最后一代中最优粒子的适应值。

步骤1初始化每个粒子。

步骤2选择每个粒子的伙伴粒子。

步骤3计算每个粒子的适应值。

步骤4计算各粒子与其榜样间的距离。

步骤5若连续F代粒子的适应值没有提升，将重选伙伴，并计算各粒子与其榜样间的距离；否则，直接跳转至步骤6。

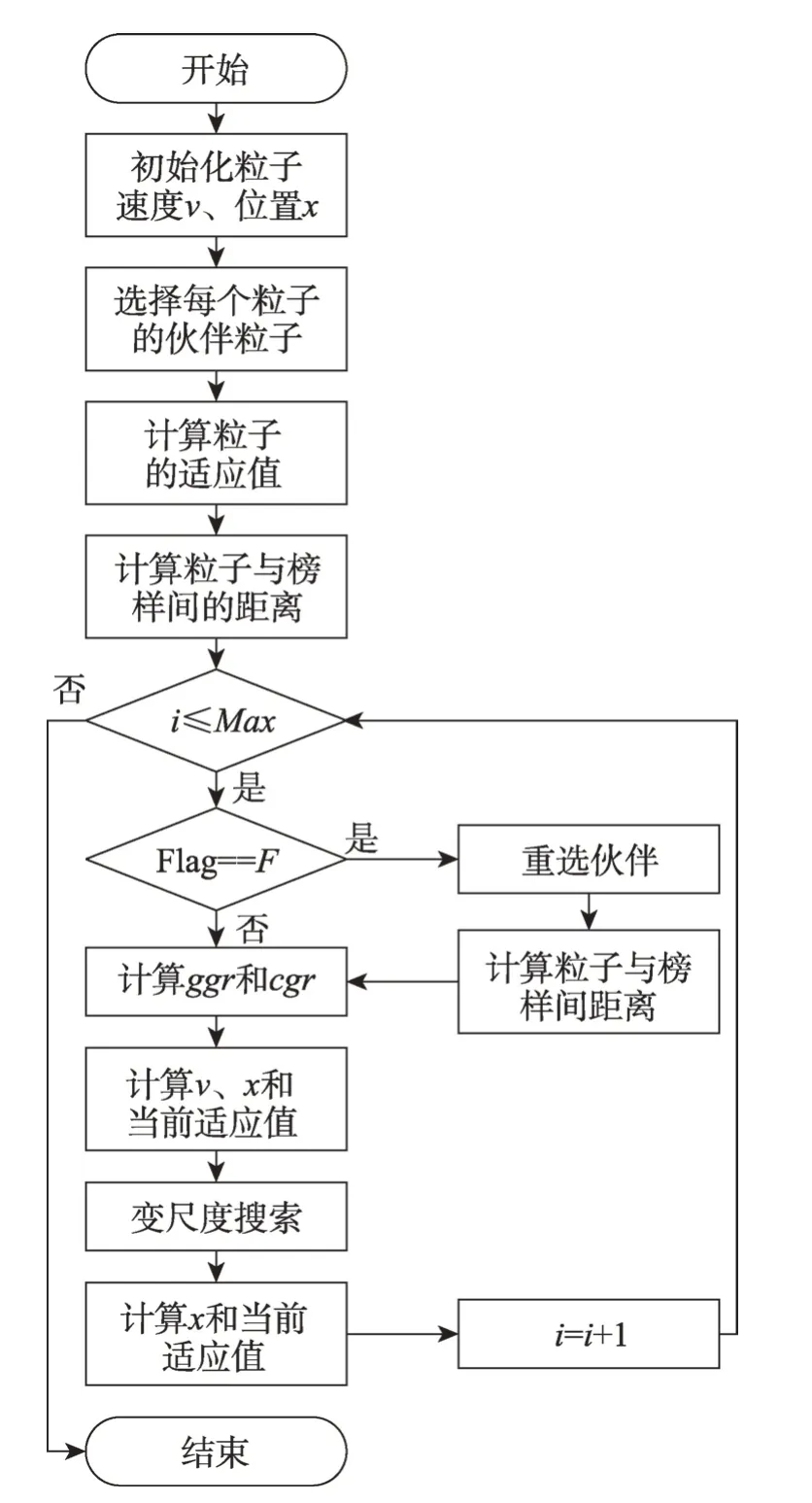
Fig.1 Flow chart of PSOSI图1 PSOSI流程图

步骤6计算每个粒子的全局引力系数ggr与伙伴引力系数cgr。

步骤7更新每个粒子的速度v和位置x，并计算粒子在当前位置的适应值。

步骤8执行变尺度搜索。

步骤9更新每个粒子的位置x，并计算粒子在当前位置的适应值。

步骤10判断是否满足结束条件，若不满足，则跳转至步骤5；否则，算法结束。

4 仿真实验及结果分析

4.1 实验设置

为了验证PSOSI算法的有效性，本文在CEC2013测试集的28 个基准函数上进行了广泛测试。这28个函数的具体信息如表1 所示，f1～f5为单峰函数，f6～f20为多峰函数，f21～f28则为复合函数[17]，在每个维度上的搜索范围均为[-100，100]。根据CEC2013 会议的统一要求，最大演化次数FEs设置为104D，其中D为解空间的维度，在本实验中设为30。同时，PSOSI的种群规模定义为50。为了获取统计结果，在以下所有实验中每种算法将在每个测试函数上独立运行30 次。

本文实验采用Xia 等人[15]提出的学习因子自适应调整方法来控制c1、c2、c3。首先，利用正态分布Ν（μi，0.12）初始化每个粒子的3 个学习因子，其中μi代表正态分布的数学期望，0.1 代表标准差。根据正态分布特性，所有粒子的学习因子都在μi的周围扰动。在搜索过程中，每个粒子会根据其当前榜样粒子的经验来调整μi，具体规则如下：

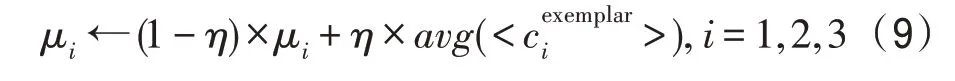
其中，η代表学习权重，并且η=0.1 时已被验证具有良好的学习效果[15]。是榜样粒子的学习因子，代表榜样粒子的学习因子均值。在每次搜索时，粒子的学习因子ci均服从Ν（μi，0.12），即ci在当前μi周围扰动。因此，只需获取初始的μi，在每次搜索时即可根据式（9）来更新当前μi，进而利用正态分布产生对应的ci。为了选取合适的初始μi，本文根据Xia 等人[15]的方法为所有粒子设置相同的初始μi，即所有粒子的初始μ1=μ2=μ3=μ。本文实验在CEC2013 测试集的28 个函数上对μ的取值进行分析，图2 展示了部分函数上不同μ对算法适应值的影响。由图2 所示，在f6、f10、f12、f28上，当μ为1.0 时，算法的适应值最低（本文中算法的适应值越低，反映其表现越好）。当μ为1.4 和1.2 时，虽然算法在f1和f22上分别表现最好，但在其他函数上表现较差。同时，当μ为1.0 时，算法在f1上的表现仅次于μ为1.3 和1.4，在f22上的表现仅次于μ为1.2。进一步地，综合考虑在28 个函数上不同μ对算法适应值的影响，本文最终将μ设置为1.0。

Table 1 Specific information of CEC2013 benchmark functions表1 CEC2013 基准函数具体信息

Fig.2 Fitness of PSOSI with different μ图2 不同μ 对PSOSI算法适应值的影响

4.2 不同策略的有效性分析

为了提高PSO 多样性和收敛性，以进一步提升其求解复杂问题的能力，本文提出三种策略，包括社会影响、引力系数和变尺度搜索。为了验证这些策略的有效性，本文对PSOSI、PSOSI-VS（PSO with social influence-variable-scale search）、PSOSI-GC（PSO with social influence-gravity coefficient）和PSO[15]进 行 比较，其中PSOSI-VS 和PSOSI-GC 分别表示去除变尺度搜索（variable-scale search，VS）和引力系数（gravity coefficient，GC）的PSOSI，图3 展示了在部分函数上的比较结果。

从图3 可以看出，在所有的12 个函数中，PSOSI的适应值和收敛速度均整体优于XPSO，这是由于PSOSI 不仅利用引力系数扩展了种群的多样性，还利用变尺度搜索提高了算法的收敛性能。同时，通过比较PSOSI-GC 和PSOSI-VS，前者在12 个函数上的收敛速度快于后者，这是因为PSOSI-GC 利用变尺度搜索增强了算法的收敛性能。另一方面，由于引力系数丰富了种群的多样性，特别是在f13、f21、f23和f24上，即使在搜索末期，PSOSI-VS 也能够找到更好的解。

为了更加直观地描述引力系数对PSOSI种群多样性的影响，以f12为例，对PSOSI-GC 和PSOSI 进行多样性比较。图4（a）和图4（c）分别是这两种算法在初始化时的种群分布图，图4（b）和图4（d）分别是迭代后期这两种算法的种群分布图。由图4（a）和图4（c）可以看出，这两种算法在初始化时的粒子分布均较为均匀。而到了迭代后期，由图4（b）和图4（d）可以看出，PSOSI 仍保持着较高的多样性，粒子分布较均匀，具有较强的进化能力。而PSOSI-GC 的多样性明显劣于PSOSI，其种群已呈现出聚集状态。

4.3 PSOSI与PSO 变体的比较

本节实验比较PSOSI 和主流的10种PSO 变体，包括F-PSO（Frankenstein’s PSO）[18]、OLPSO（orthogonal learning PSO）[19]、DEPSO（differential evolution and PSO）[20]、PSODDS（PSO using dimension selection methods）[21]、CCPSO-ISM（competitive and cooperative PSO with information sharing mechanism）[22]、SRPSO[16]、HCLPSO（heterogeneous comprehensive learning PSO）[23]、GLPSO（genetic learning PSO）[24]、EPSO（ensemble PSO）[25]

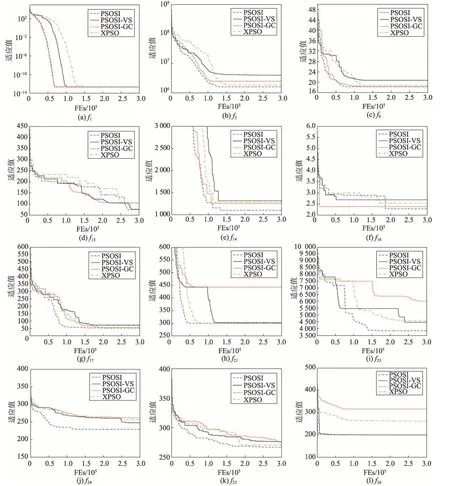
Fig.3 Comparison of fitness with respect to different strategies图3 不同策略的适应值比较

和XPSO[15]。这些算法均采用其原始论文中的参数设置。每种算法都独立运行30 次，表2 至表4 展示了这11种算法的适应值均值，并以粗体和下划线标记这些算法中的最好结果。为了体现各算法的综合性能，表5 对这11种算法进行通用的弗里德曼检测（显著性水平α=0.05）。另外，表6 还对这11种算法进行了实时比较。

Fig.4 Population fitness distribution of PSOSI-GC and PSOSI图4 PSOSI-GC 和PSOSI种群适应值分布

Table 2 Mean fitness comparison of 11 algorithms on 5 unimodal functions on CEC2013 test suite表2 11种算法在CEC2013 测试集5 个单峰函数上的平均适应值比较

表2 比较了这11种算法在5 个单峰函数上的平均适应值。由表2 可以看出，PSOSI 在f4上获得最好的平均适应值，而OLPSO、PSODDS、XPSO 和GLPSO则分别在f1、f2、f3和f5上获得最优的平均适应值。根据表5 中的弗里德曼测试结果，可以看出PSOSI 在这5个单峰函数上获得最佳的综合表现，其排名为3.40，优于其他10种算法。

表3 比较了这11种算法在15 个多峰函数上的平均适应值。由表3 可以看出，PSOSI 在f8、f10、f13和f18上获得最好的平均适应值。同时，结合表5 可以看出，尽管PSOSI 在这15 个多峰函数上仅获得次优的综合表现。与取得最优表现的GLPSO 相比，PSOSI 的平均排名仅低了0.40。

表4 比较了这11种算法在8 个复合函数上的平均适应值。由表4 可以看出，PSOSI 在f24和f28这两个函数上获得最好的平均适应值。同时，结合表5 可以看出，PSOSI 在这8 个复合函数上获得最佳的综合表现，其排名为3.13，比次好的GLPSO 在平均排名上高了1.0。

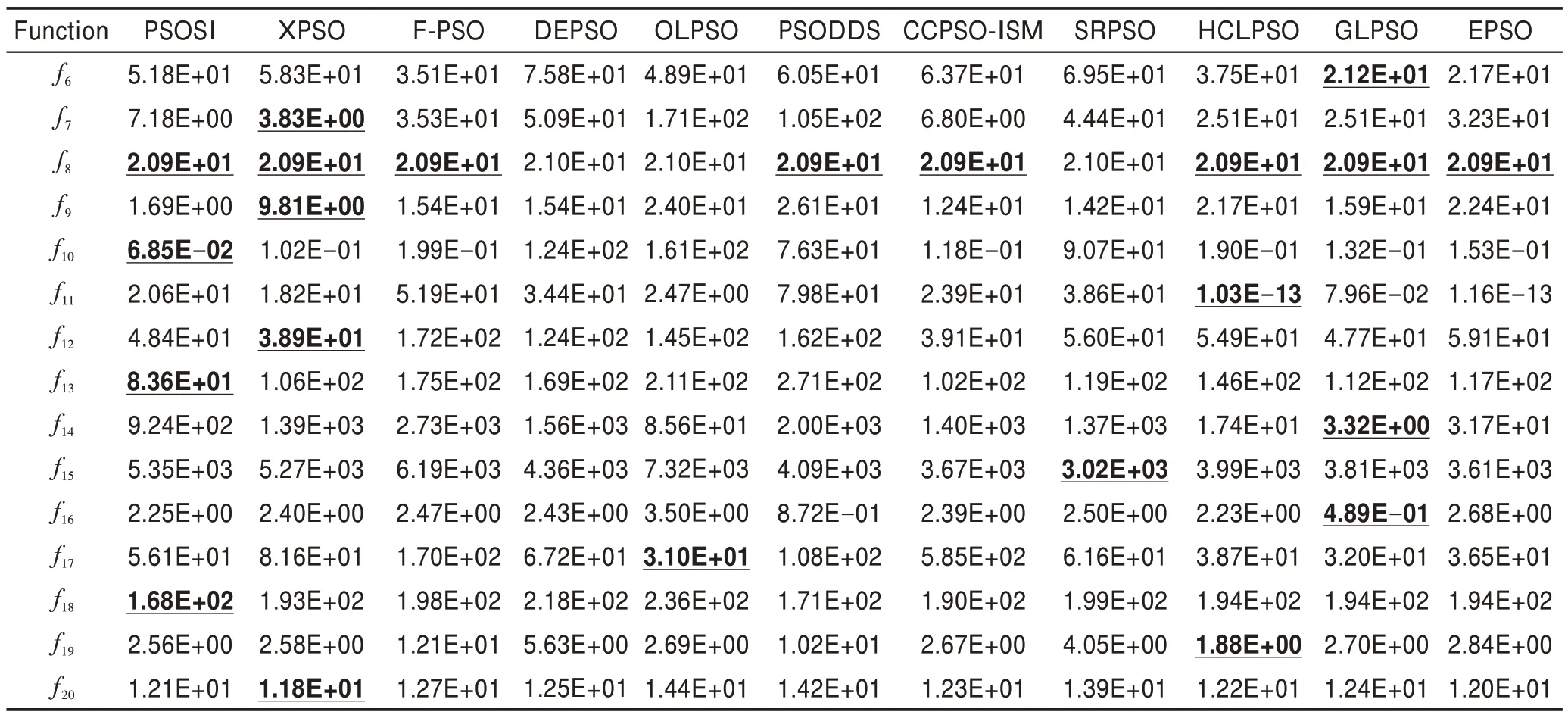
Table 3 Mean fitness comparison of 11 algorithms on 15 multimodal functions on CEC2013 test suite表3 11种算法在CEC2013 测试集15 个多峰函数上的平均适应值比较

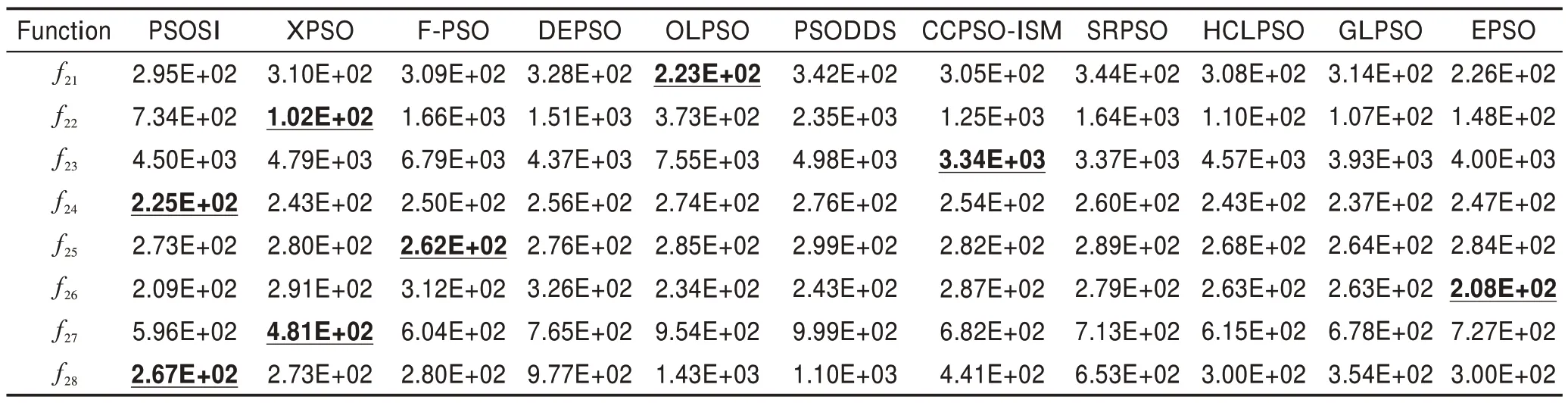
Table 4 Mean fitness comparison of 11 algorithms on 8 composition functions on CEC2013 test suite表4 11种算法在CEC2013 测试集8 个复合函数上的平均适应值比较

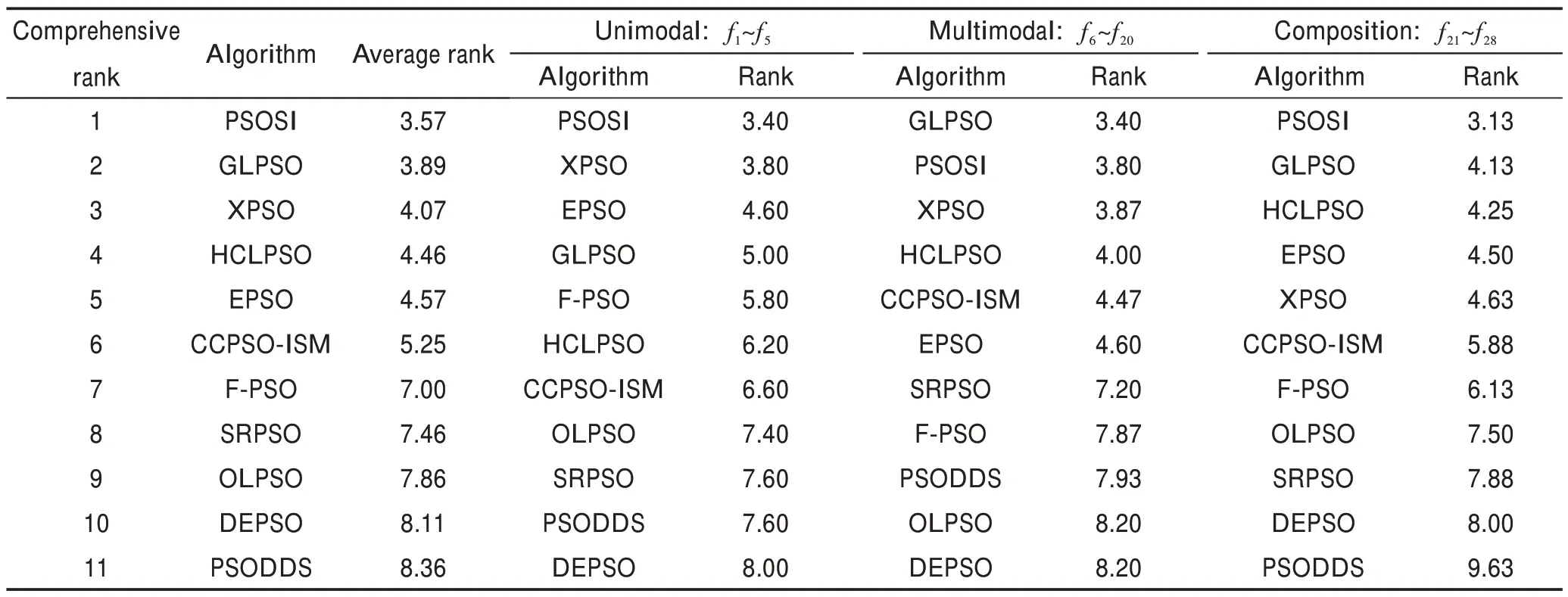
Table 5 Friedman test of 11 algorithms on CEC2013 test suite表5 11种算法在CEC2013 测试集上的弗里德曼检测

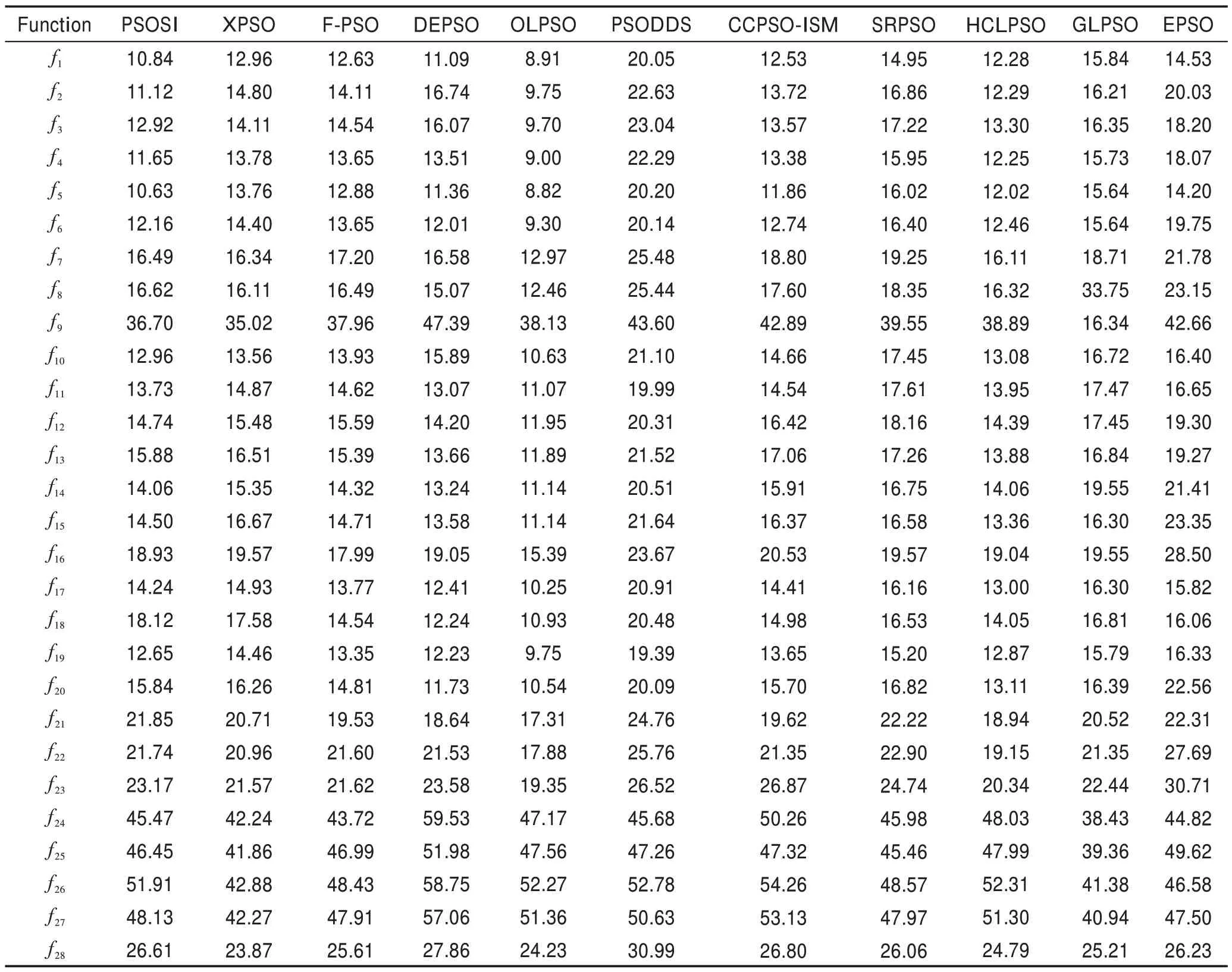
Table 6 Time comparison of 11 algorithms on CEC2013 test suite表6 11种算法在CEC2013 测试集上的耗时比较 s

从表6 中可以看出，在f1～f5这5 个单峰函数上，PSOSI 的时间耗费仅比OLPSO 长，比其他9种PSO的变体算法快。在其他的复杂函数上，PSOSI 比起其在单峰函数上的表现，时间耗费排名有所下降，这是由于PSOSI需要频繁地更新伙伴粒子，并计算引力系数，以进行社会学习。幸运的是，在3.4 节的分析中，PSOSI 的时间复杂度与标准的PSO 保持相同。同时考虑到表5 中PSOSI 出色的综合表现，这些额外的时间耗费是可以接受的。

4.4 PSOSI与其他优化算法的比较

为了进一步验证PSOSI 的有效性，在本节中将PSOSI 和其他3种非PSO 算法进行比较，这3种算法包括CoDE（DE with composite trial vector generation strategies and control parameters）[26]、TPC-GA（GA with three-parent crossover）[27]和MABC-NS（modified ABC with neighborhood search）[28]，分别属于差分进化算法、遗传算法和人工蜂群算法的变体。表7 展示了这4种算法的平均适应值和通用的弗里德曼检测（显著性水平α=0.05）。

从表7 中可以看出，PSOSI在这28 个函数上的10个函数中取得了最好的平均适应值，这10个函数包括f3、f7、f8、f9、f10、f20、f24、f25、f27和f28。此外，PSOSI 在28个函数上以2.11 的平均排名获得了最佳的综合性能。

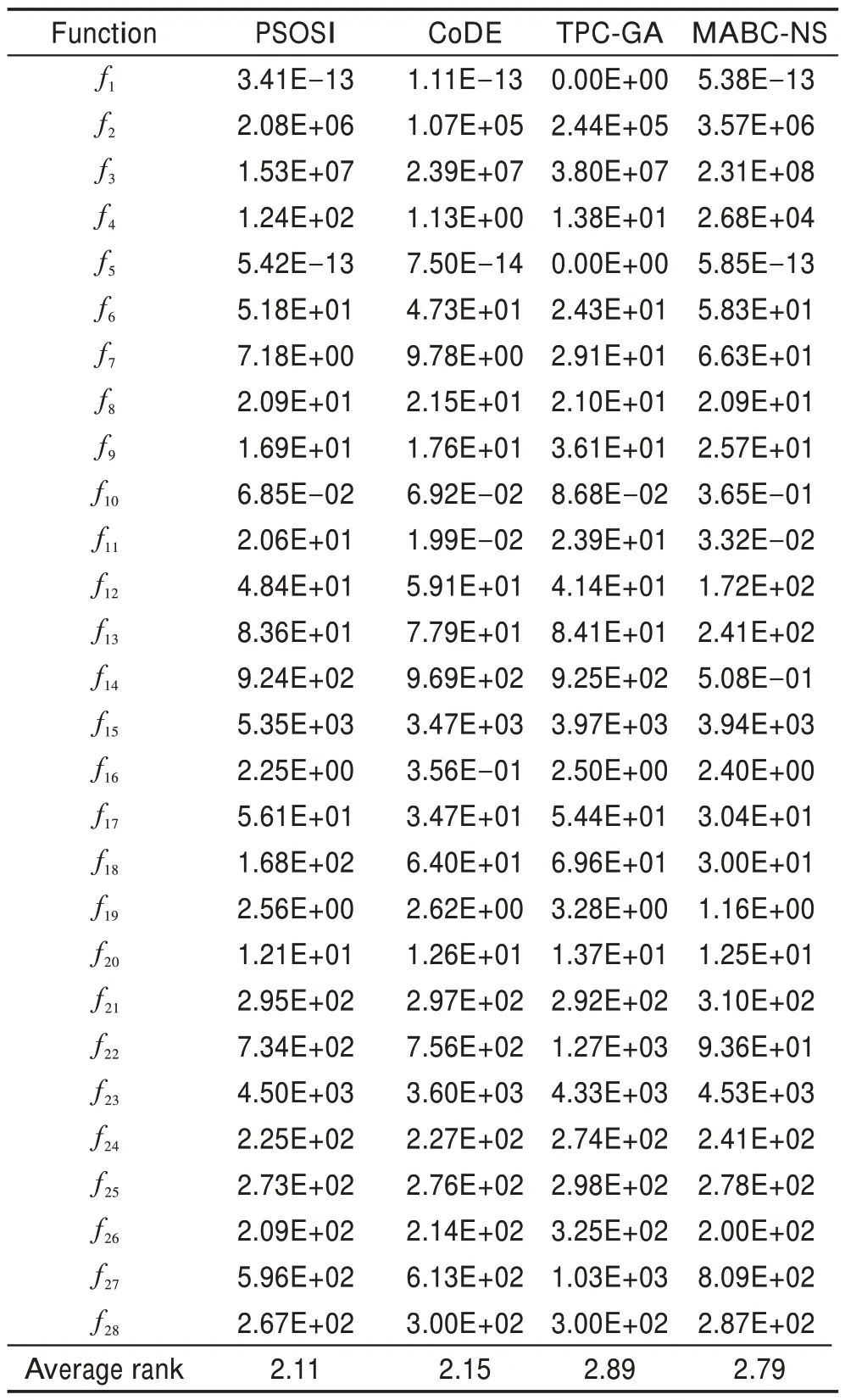
Table 7 Mean fitness comparison of PSOSI and three other optimization algorithms on CEC2013 test suite表7 PSOSI与其他3种优化算法在CEC2013测试集上的平均适应值比较

5 结束语

本文提出了一种融入社会影响力的粒子群优化算法。首先，每个粒子将选择全局最优粒子和最优伙伴粒子作为其“社会学习”的对象，从而为每个粒子带来更丰富的有用知识。其次，引入引力系数分别描述各榜样带来的影响，在保证最优经验得到分享的同时，更多地是增强了种群学习的多样性。此外，每个粒子还在各维度上进一步向其最优伙伴粒子学习，实现从全局到局部的变尺度搜索，增强算法的整体收敛能力。为了验证所提出方法的有效性，在CEC2013 测试集上将其与主流的10种PSO 变体及3种其他优化算法进行比较。实验结果表明，PSOSI的表现优于以上其他算法。

在未来的工作中，将结合PSOSI和一些表现良好的演化计算或群体智能算法，考虑这些方法的优缺点及结合点，以进一步提高复合优化算法的性能。