带核方法的判别图正则非负矩阵分解*

2020-11-15李向利

计算机与生活 2020年11期

关键词：正则聚类矩阵

李向利，张颖

1.桂林电子科技大学数学与计算科学学院，广西桂林 541004

2.广西密码学与信息安全重点实验室，广西桂林 541004

3.广西自动检测技术与仪器重点实验室，广西桂林 541004

4.广西高校数据分析与计算重点实验室，广西桂林 541004

1 引言

随着信息技术的发展，在许多实际的应用如模式识别、计算机视觉中，需要处理的数据通常都是高维数据。这可能导致“维数灾难”，给数据处理带来很大的挑战。为了解决这个问题，研究者们提出了很多降维方法，例如主成分分析（principal component analysis，PCA）[1]、线性判别分析（linear discriminant analysis，LDA）[2]、奇异值分解（singular value decomposition，SVD）[3]和非负矩阵分解（nonnegative matrix factorization，NMF）[4]。目前，最流行的降维方法是NMF。NMF 将非负的数据矩阵分解成两个非负的因子矩阵的乘积，其中一个称为基矩阵，一个称为系数矩阵（也称为低维的表示矩阵）。由于非负约束的存在，NMF 只允许使用加法运算进行线性组合，这使得NMF 的分解结果是基于部分表示的。从心理学和生理学角度来说，NMF 的分解结果是符合人类局部相加构成整体这一认知的，具有较强的解释性。

非负矩阵分解不仅是一种有效的降维方法，而且在图像聚类上有广泛的应用，这是因为NMF 的目标函数可以从聚类的角度解释，并且在文献[5-6]中已经证明非负矩阵分解与许多聚类算法如K-means、核K-means 以及谱聚类算法有一定的等价性。最初的NMF是由Lee等人[4]于1999年提出的，并在文献[7]中给出了原始模型的迭代规则。基于标准的NMF，很多学者提出了改进的版本，例如Cai等人[8]提出了图正则非负矩阵分解（graph regularized NMF，GNMF）。但是，初始版本的NMF 以及GNMF 存在一些不足，它们都是无监督的方法，没有使用有标签数据的标签信息。然而，在大部分实际应用中获得的实验数据通常都会有一部分数据已知标签信息。充分使用这些已知的标签信息能够显著地提高聚类效果。为此，学者们在NMF 模型上加入标签约束，提出半监督的NMF，例如判别非负矩阵分解（discriminative NMF，DNMF）[9]。然而，单纯的半监督方法只使用了数据的标签信息，并不能捕获数据固有的几何结构信息。

上述的NMF 方法都是线性的方法，只能够处理线性分布的数据，不能够很好地处理数据是非线性的情况。常用的解决非线性分布数据的方法是核方法，这种方法也是一种经常使用的非线性特征提取方法。核方法的基本思路是先寻找一个从原始数据空间到一个高维核空间的非线性映射，使得数据在映射之后是线性可分离的，然后在这个核空间中运行一般的线性方法，例如NMF 等。由此可以拓展出许多的基于核方法的算法，比如核主成分分析（kernel PCA，KPCA）[10]、核线性判别分析（kernel LDA，LDA）[11]以及核非负矩阵分解（kernel NMF，KNMF）[12]。但是，KNMF 既没有保存数据的几何结构信息，也不是一种半监督的方法，没有充分使用标签信息，因此聚类效果也受到限制。

为此，受核方法以及基于图的判别非负矩阵分解的启发，本文提出基于核的判别图正则非负矩阵分解（discriminative and graph regularized nonnegative matrix factorization with kernel method，KGDNMF）。该方法是一种半监督的方法，通过部分有标签数据的标签构造标签矩阵，使得具有相同标签的数据分解后的表示对准同一个轴。能够充分地使用标签信息，利用标签信息引导无标签数据聚类，相比无监督方法有更好的聚类效果。该方法在NMF 的框架上加入了图正则项，能够探索数据固有的几何结构，克服了原始NMF 忽略数据流形结构的问题。同时，该方法结合了核方法，能够处理一般NMF 处理不了的非线性分布数据，提高了聚类效果。

2 相关工作和预备知识

基于Lee 等人[4]提出的标准的NMF，很多学者提出了改进的NMF，在标准的NMF 的框架中增加一些有必要的约束，提高分解数据的聚类效果。Ding 等人[13]提出了凸非负矩阵分解（convex NMF，CNMF）。CNMF 通过使用原始数据的非负线性组合来表示基矩阵，使得所得到的基矩阵更能体现作为一个聚类的中心的性质。同时，这样得到的系数矩阵相比标准的NMF 更加稀疏。为了得到更加稀疏的结果，Hoyer[14]提出了非负稀疏编码（non-negative sparse coding，NNSC），该方法通过对编码矩阵加上l1范数约束来增强分解结果的稀疏性，提高了聚类效果。Cai等人[8]提出了图正则非负矩阵分解（GNMF），通过构造数据的图拉普拉斯矩阵来探索数据固有的几何结构，显著提升了聚类性能。文献[15]和文献[9]分别提出了两种判别非负矩阵分解（DNMF）。文献[15]通过将LDA 整合到NMF 框架中，来捕获数据的判别信息。而文献[9]则通过构造标签矩阵，使得有相同标签的数据分解后的表示（系数矩阵）对准同一个轴。显然DNMF 是一种半监督的聚类方法，需要使用部分已知标签数据的标签信息。Li 等人[16]在DNMF 的框架中加入图正则项提出基于图的判别非负矩阵分解。Wang 等人[17]提出最大最小距离非负矩阵分解（max-min distance NMF，MMDNMF），最小化最大类内距离，最大化最小类间距离来捕获判别信息，提高聚类效果。文献[18]针对样本具有的先验信息是成对关系约束的情况，提出了一个相对成对关系约束非负矩阵分解（relative pairwise relationship constrained NMF，RPR-NMF），通过对相对成对关系的数据之间的距离进行惩罚，使得数据点分解后与原始数据保持相似的相对关系。Peng 等人[19]提出了一个基于超平面的非负矩阵分解，该方法为每个类构造一个超平面，使得有标签的数据点靠近对应的超平面。

上述的NMF 变体都是针对数据是线性分布的情况的。针对数据非线性分布的情况，文献[20]和文献[21]将核方法与NMF 结合提出了核非负矩阵分解。使用核方法可以采取的核函数也是多种多样的。在文献[20]中，采用的核函数是多项式核函数，文献[21]则将多项式核函数拓展为分数阶内积核。

下面将给出本文的相关预备知识。

2.1 非负矩阵分解

给出非负数据矩阵X=[x1，x2，…，xn]∈Rm×n，其中xi∈Rm表示一个数据。标准的NMF 模型是将数据矩阵X分解成一个非负的基矩阵U∈Rm×k和一个非负的系数矩阵V∈Rn×k的乘积，这里k是降维的维数。为了找到近似的X≈UVT，文献[4]给出了两种损失函数，分别是采用欧氏距离的平方和广义的Kullback-Leibler 散度。一般的，采用欧氏距离的平方作为损失函数可以构造如下的优化问题：

其中，||∙||F表示矩阵的Frobenius范数。

显然，优化问题（1）是非凸的，求解这个问题的全局最优解是非常困难的。然而，当固定两个变量中的一个去求解另一个最优解就是一个凸优化问题。因此，文献[7]提出了一种交替迭代两个变量的乘性迭代规则。

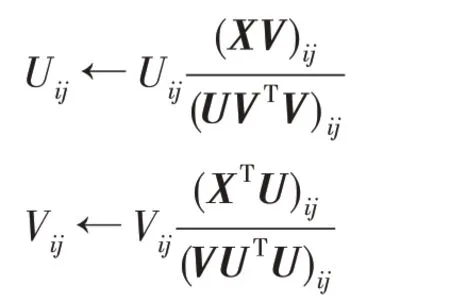
2.2 图正则非负矩阵分解

基于标准的NMF，Cai 等人[8]提出了图正则非负矩阵分解（GNMF）。假设X表示数据矩阵，每一列表示一个数据。如果在原始的高维数据空间中，数据点xi和xj相距比较近，那么在降维之后的空间中，新的数据表示vi和vj也应该相距很近。构造一个权重矩阵W来度量两个数据点之间的相似性，通常使用的0-1 度量定义如下：

通常使用欧氏距离来测量数据点之间的距离，则有：

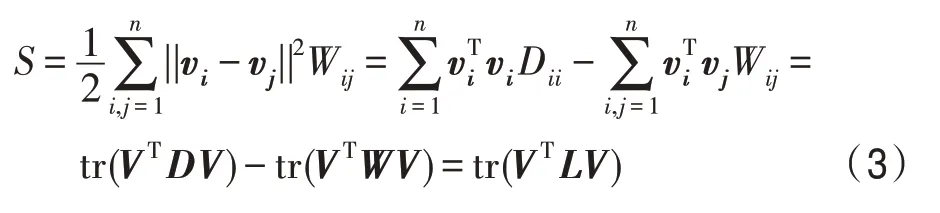
2.3 判别非负矩阵分解

2.4 核非负矩阵分解

3 带核方法的判别图正则非负矩阵分解

3.1 算法

在NMF 标准模型（1）中，系数矩阵V给出了原始高维数据矩阵X基于部分的降维表示。但是这个模型并未给出数据固有的几何结构和判别信息，并且该模型只能够处理线性可分离的数据。GNMF[8]能够很好地描述数据空间的几何结构，DNMF[9]能够使用部分有标签数据给出判别信息，而核方法能够处理非线性的情况。结合这三种方法到NMF 中，可以得到本文提出的带核方法的判别图正则非负矩阵分解（KGDNMF）。

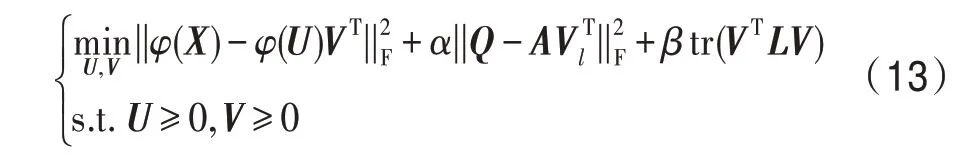
模型中φ是从原始数据空间到核空间的映射，核函数采用多项式核。Q是根据式（5）构造的标签矩阵，有标签的数据个数为p。Vl是V无标签数据对应部分全部取0。L=D-W是Laplace 矩阵，其中Dii=∑jWij，W是相似度权重。关于权重选择有热核权重、0-1 权重、内积权重等，本文选择0-1 权重。α＞0 和β＞0 是各个正则项的平衡参数。

一般NMF 采取交替迭代更新的方法进行求解，而迭代更新初始的U和V是随机给出的，这个随机性会影响实验的结果。为了解决这个问题，本文采用了一种“热启动”的策略[22]。首先对数据进行一次K-means 聚类，得到一组聚类中心，然后将这些聚类中心作为初始的基矩阵U0。为此，在优化问题（13）上加上正则项。可以得到：

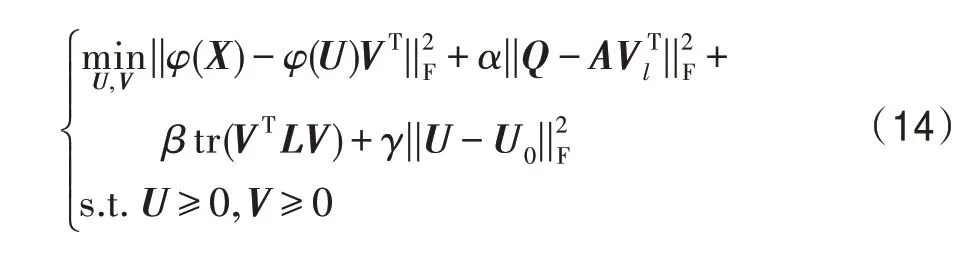
显然，优化问题同时求解U、V和A是非凸的，但是分别求解是凸的。因此，采用交替更新迭代的方式求解。目标函数可以展开为：

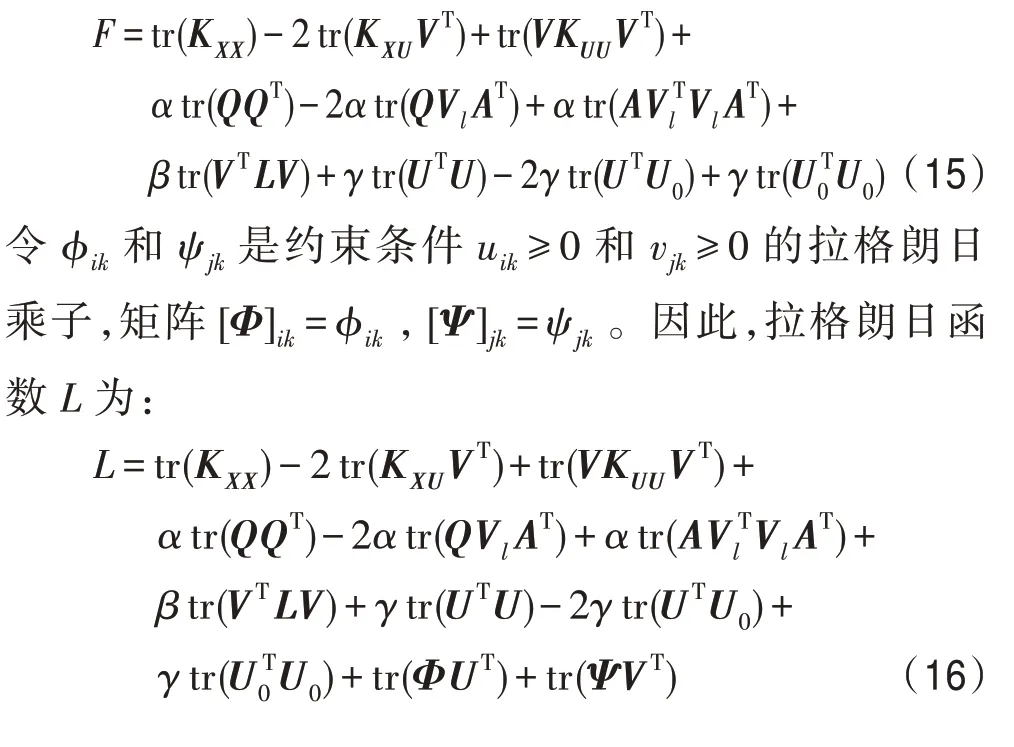
3.2 收敛性证明

根据上面提出的交替迭代更新算法，有如下的定理。

定理1优化问题（14）在迭代更新公式（17）～（19）下是非增加的。当且仅当U、V和A到达一个稳定点时目标函数值不变。

下面将证明定理和文献[16]相似，本文引入辅助函数证明V在更新规则下的收敛性，U的收敛性也可以相似证明。关于辅助函数有如下引理成立。

引理1对函数F（x）存在辅助函数G（x，x′）满足G（x，x′）≥F（x）且G（x，x）=F（x），那么F（x）在如下的更新规则下时非增加的：

下面证明对每一个vab，都是按照式（20）的规则更新的。

引理2假设F′表示对变量V的一阶导数，那么函数（23）是Fvab的辅助函数。

综合式（26）～式（28），不等式（25）成立。因此式（23）定义的函数是Fvab的辅助函数。

辅助函数（23）在更新规则式（20）下得到的迭代公式正是关于V的迭代公式。因此定理关于V成立。关于U的部分可以类似证明。由于优化问题关于A是无约束的凸优化问题，更新公式是直接求解直接得到的，因此关于A也是收敛的。故定理是成立的。

4 实验与分析

本章中，将本文提出的算法在COIL20、MNIST和Yale 人脸数据集3 个图片数据集上运行，并与Kmeans、NMF、GNMF、DNMF、GDNMF（discriminative nonnegative matrix factorization）进行比较。为了能够更好地验证算法的性能，首先从数据集中随机选择k类数据，对每个选出的数据子集重复10 次实验，并计算平均聚类性能。对于半监督聚类算法（DNMF、GDNMF 和KGDNMF），从每一类中随机选择20%作为有标签数据。对于降维算法，降维维数采用聚类数目，然后对降维后新的数据表示使用K-means 进行聚类。每次实验中K-means 进行20 次，取最好的结果。对于实验效果，使用准确率（accuracy，ACC）和互信息（mutual information，MI）作为评价指标，ACC 和MI的计算方法参考文献[8]。

4.1 参数选择

本文提出的算法有3 个平衡参数，α、β和γ。下面将从实验分析参数对聚类结果的影响并选择最优参数。对COIL20，选择20 个类进行实验；对MNIST 选择10 个类，每类选择2 000 个图片进行实验；对于Yale 人脸数据集，使用所有数据进行实验。重复10次实验，然后取平均值。具体实验结果见图1～图3。从图中可以看出，在COIL20 数据集上，选择参数α=100.0，β=0.1，γ=100.0 ；在MNIST 数据集上，选择参数α=100.0，β=5.0，γ=0.2 ；在Yale 人脸数据集上，选择参数α=20.0，β=20.0，γ=5.0。

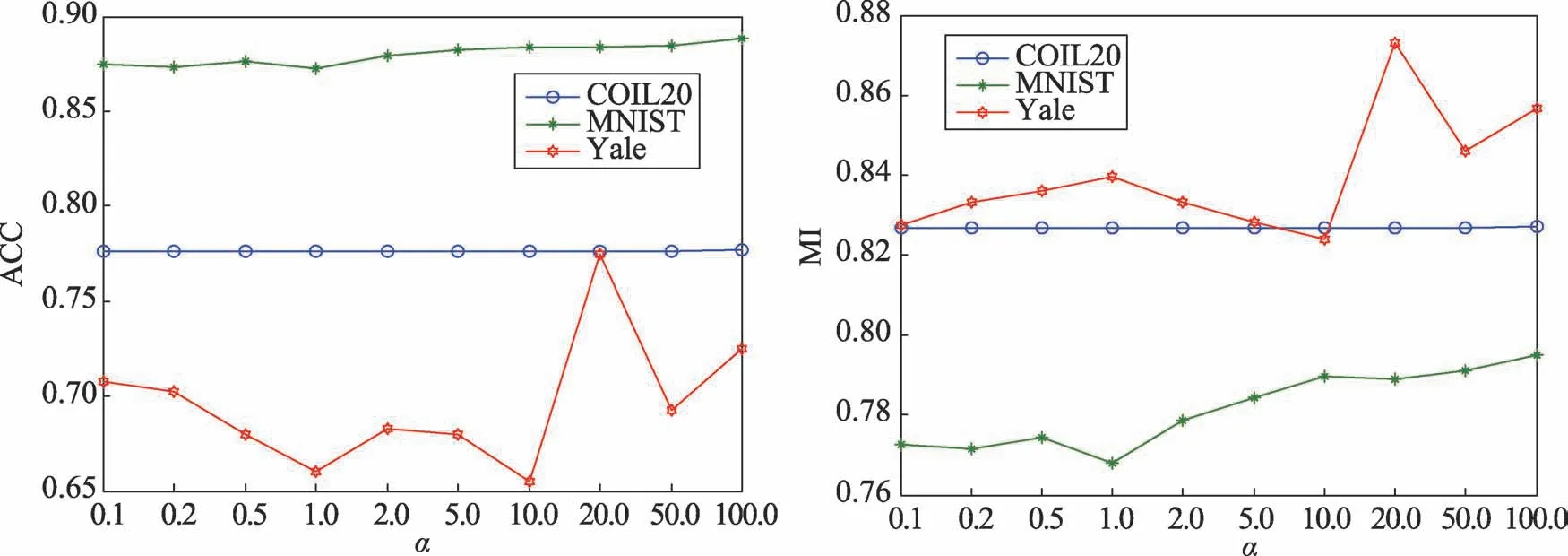
Fig.1 Influence of parameter α on experimental results图1 参数α 对实验结果的影响

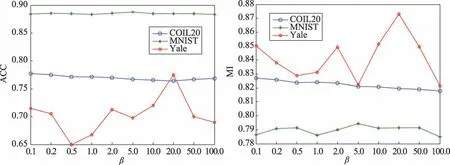
Fig.2 Influence of parameter β on experimental results图2 参数β 对实验结果的影响

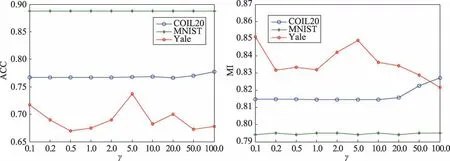
Fig.3 Influence of parameter γ on experimental results图3 参数γ 对实验结果的影响

4.2 COIL20 数据集实验结果

COIL20 数据集包含20 个物体的总共1 440 张图片，每个物体72 张。将每张图片处理成32×32 像素大小。所有的实验结果展示在表1中。相比GDNMF，KGDNMF在ACC和MI上平均分别有0.044 0和0.025 8的提高。相比GNMF 和DNMF，KGDNMF 在ACC 上平均分别有0.053 8 和0.137 5 的提高，在MI上分别有0.032 5 和0.165 7 的提高。对比实验结果可以发现KGDNMF 相比其他几种方法，在聚类结果的准确率（ACC）和互信息（MI）上均有所提高。

4.3 MNIST 数据集实验结果

MNIST 是手写数字图片数据集，包含手写数字0～9 训练样本60 000 张，测试样本10 000 张。本次实验，从训练样本中每类选择200 张作为实验数据集，每张图片处理成28×28 像素大小。实验结果展示在表2 中。对比实验结果可以发现，KGDNMF 相比其他方法，在ACC 和MI 两个指标上都有提高。与GDNMF 相比，在聚类类数较少时，聚类效果提升不多，但是随着聚类数目增加，KGDNMF 表现越优越。相比GNMF 和DNMF，KGDNMF 在ACC 上平均分别有0.167 8 和0.241 4 的提高，在MI 上分别有0.166 6和0.442 8 的提高。

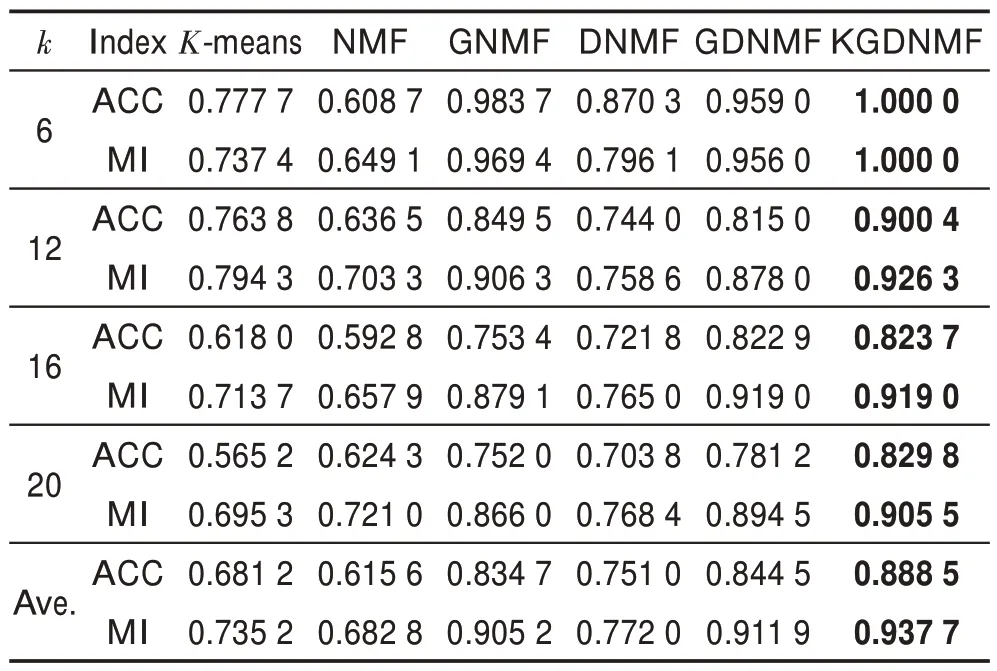
Table 1 Experimental results on COIL20 dataset表1 COIL20 数据集实验结果

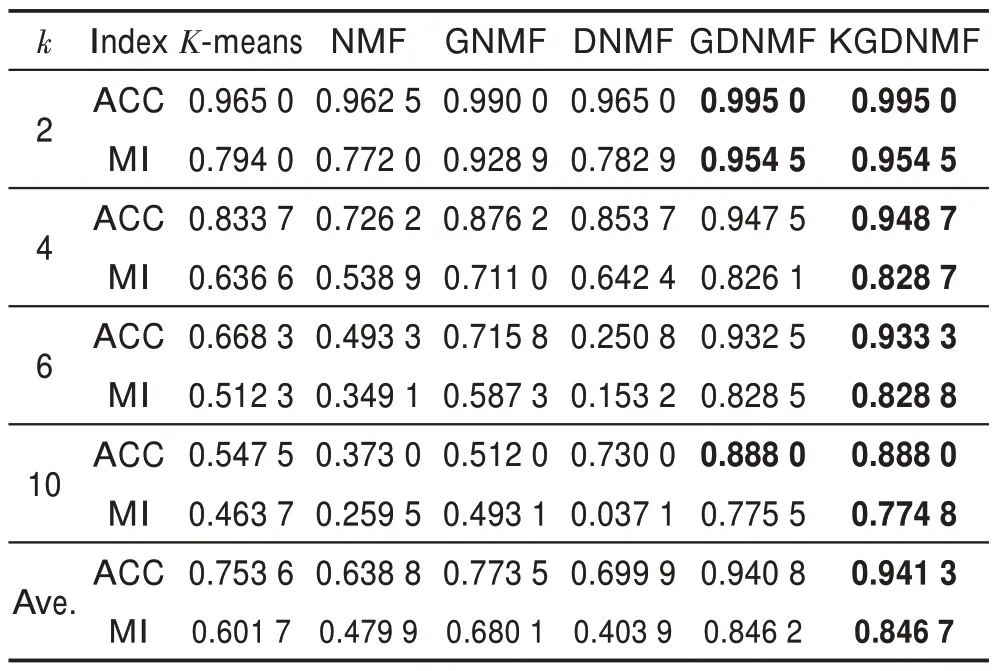
Table 2 Experimental results on MNIST dataset表2 MNIST 数据集实验结果

4.4 Yale人脸数据集实验结果

Yale是人脸图片数据集，包含40个人不同表情光照下的图片共400 张，每个人10 张图片。本次实验，每张图片处理成32×32 像素大小。实验结果展示在表3 中。从实验结果可以看出，大部分情况效果最好的算法还是KGDNMF。相比KGDNMF，GDNMF 在ACC 和MI平均分别低0.017 6 和0.005 1；DNMF 在ACC 和MI上平均分别低0.414 6和0.424 5；GNMF 在ACC 和MI 上平均分别低0.155 3 和0.106 0。综合来说还是KGDNMF 聚类效果最好。

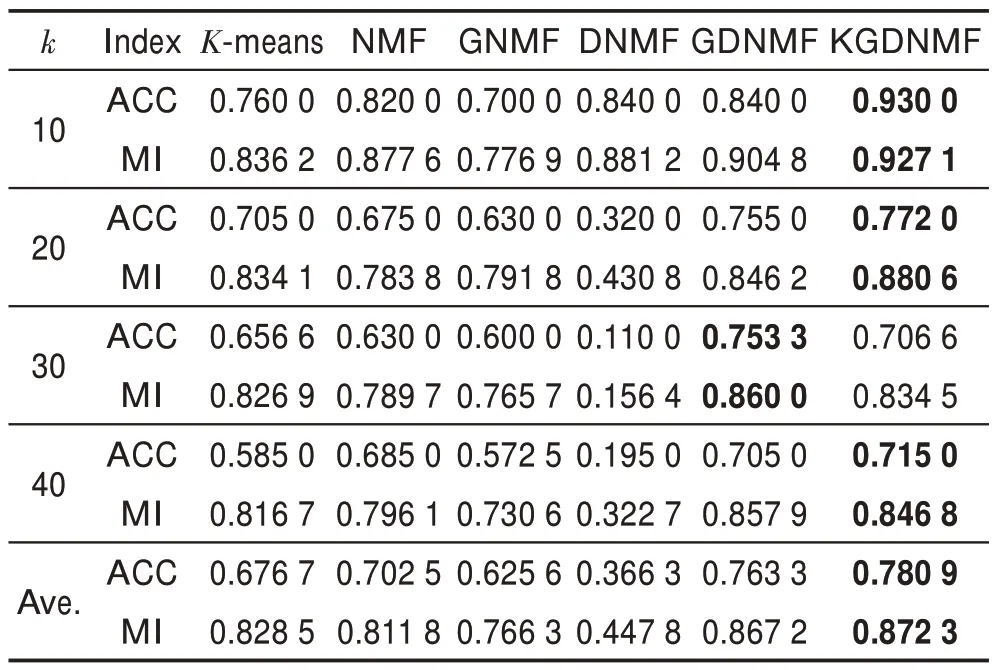
Table 3 Experimental results on Yale face dataset表3 Yale人脸数据集实验结果

4.5 实验结果分析

分析上述3 个数据集的实验结果，在大部分情况下效果最好的算法还是KGDNMF。这是由于KGDNMF 同时采用了图正则项和核方法，还是半监督的方法。而GDNMF 没有采取核方法，只能处理数据是线性分布的情况；DNMF 只使用了标签矩阵约束，无法保存数据的几何结构；GNMF 只加入了图正则项，是一种无监督的方法，对比半监督的KGDNMF效果要差。