扣压力失效状态下WJ-8 扣件垂向力学行为研究
2020-11-14赵闻强侯博文
高 亮,赵闻强,侯博文
(北京交通大学土木建筑工程学院,北京 100044)
高速铁路无砟轨道扣件系统联结了钢轨与下部无砟轨道,并传递列车动载至下部无砟道床。扣件系统工作时主要通过螺栓、道钉压紧弹条,使之发生形变并扣压钢轨,从而起到了保持钢轨稳定几何形位的功能。但随着运营时间的增长,扣件系统服役状态的劣化不可避免。在循环动荷载和其他长期环境荷载的作用下,扣件会逐渐出现扣压力损失、弹条松动松脱等现象。退出正常工作状态的扣件系统降低了钢轨承载稳定性,影响了高速列车的安全、平稳运营,严重时甚至可能导致脱轨事故。
许多研究通过车辆-轨道耦合动力学理论建立了相关动力学模型来评估扣件失效对车辆-轨道系统动力响应特性的影响。肖新标等[1]等基于轮轨耦合动力学理论分析扣件失效工况下直线轨道-车辆系统的动态响应。张斌[2]运用车辆轨道系统振动分析数值方法,研究了地铁扣件失效对轨道振动特性的影响。朱剑月[3]建立了基于连续弹性离散点支承梁的钢轨模型,分析了列车运行速度与扣件失效数量对轨道结构动力性能的影响。余关仁等[4]等研究了扣件和隔振器失效对浮置板动力响应特性的影响。徐启喆等[5]建立了不同失效情况的扣件模型,分析了扣件失效对钢轨变形及转角的影响。在上述研究中,扣件大多被简化为多点支承的弹簧-阻尼单元,并在失效处将扣件刚度属性折减或去掉弹簧单元来实现扣件失效的模拟,弹簧单元垂向刚度也简化为线性。这种模拟方式可以用来模拟扣件垫板脱出的失效场景,但不适用于扣件处于扣压力失效的情况。针对扣压力失效,应选择更合适的模型来描述其失效后的垂向非线性力学行为。
Oregui 等[6]建立了不同类型的扣件简化模型,研究了扣件模型建模方式对单节轨枕轨道垂向动力学的影响;王开云等[7]考虑扣件系统扣压件的预压力,建立了扣件垂向动力分析模型,分析了扣件垂向振动特性。这些研究建立了更加精细的扣件模型[8],为本文研究扣件的垂向非线性行为提供了一定的思路,但在代入车辆-轨道大系统计算时也存在计算代价较大等问题。针对高速铁路扣件断裂的问题,朱胜阳、尚红霞等[9 − 10]还通过非线性接触理论建立扣件实体模型,从结构本身探究了扣件断裂的原因,这亦为本文提供了方法上的参考。
本文以目前应用较为广泛的高速铁路CRTSIII型板式无砟轨道及其配备的有挡肩扣件WJ-8 扣件系统为例,通过建立扣件系统的精细化分析模型揭示了扣件扣压力失效后自身的垂向非线性力学行为;提出了扣件扣压力失效的简化模拟方法,使之既能保证原有车轨模型中扣件简化模型的计算效率,也能够反映一定的垂向非线性刚度特征;最后分析了不同失效类型对车辆-轨道系统动力响应的影响。本文的计算结果能够为高速铁路扣件结构优化、扣件病害检测等领域提供一定的理论参考。
1 WJ-8 扣件精细化分析模型
1.1 扣件系统部件的精细化模拟
基于材料弹塑性本构和非线性接触理论,本文采用ABAQUS 软件对扣件系统进行精细化建模。WJ-8 扣件系统由螺旋道钉、平垫圈、弹条、绝缘块、轨距挡板、轨下垫板、铁垫板、铁垫板下弹性垫板以及定位于下部轨道混凝土中的预埋套管组成[11],如图1 所示。具体建模时,钢轨为CHN60 钢轨,轨距挡板采用7 号轨距挡板,螺旋道钉和绝缘块分别选用S2 型螺旋道钉和WJ8-Ⅰ型绝缘块。钢轨、道钉、绝缘轨距块等部件采用线性减缩六面体单元进行建模。WJ-8 扣件弹条可分为W1 型和X2 型。本文选用W1 型弹条,并采用改进的二次四面体单元进行建模以保证计算的收敛性和准确性,每根弹条包含26421 个单元。

图1 WJ-8 扣件系统主要部件组成Fig. 1 Main components of WJ-8 fastener
WJ-8 扣件系统通过铁垫板下弹性垫板为系统提供必要的弹性[12 − 13]。本文以适用于高速线路的B 类铁垫板下弹性垫板为例,其垫板静刚度取为23 kN/mm(±3 kN/mm),扣件整体节点静刚度相应取为30 kN/mm(±10 kN/mm)。模型考虑垫板静刚度属性及面支承效应,在铁垫板下采用三向弹簧-阻尼单元模拟弹性垫板,且为垂向为只受压弹簧。
WJ-8 扣件系统精细化分析模型考虑了弹条等金属部件的理想弹塑性材料本构,并采用双线性强化模型对其弹塑性行为进行描述[14],其应力-应变关系可概括为:

式中:E是弹性模量;Eh为强化模量;σy和εy分别是屈服应力和屈服应变。
当材料进入塑性状态后,试件横截面积的变化对材料性能的影响不能被忽视。因此在定义双线性强化模型时,需要将工程应力-应变数据转换为有限变形中面积改变的真应力-应变曲线:

式中:σtrue和εtrue为分别为真实应力和真实应变;σnorm和εnorm分别为名义应力和名义应变。
扣件精细化分析模型的具体建模参数见表1。
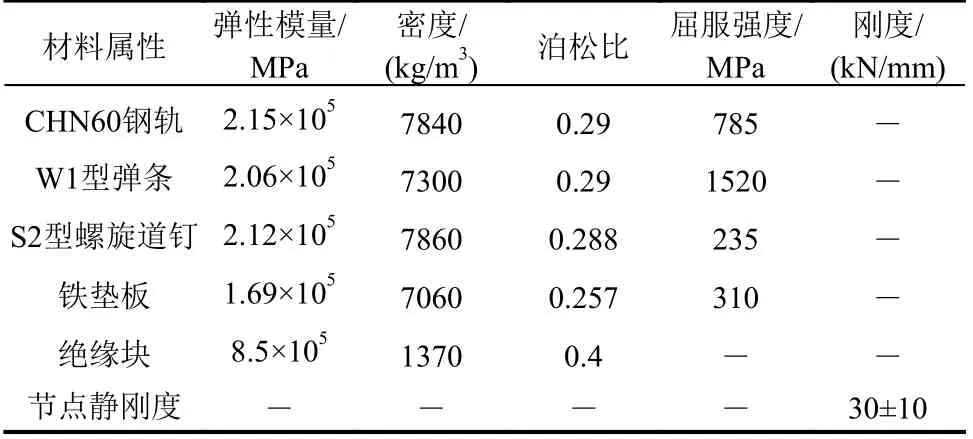
表1 WJ-8 扣件精细化分析模型建模参数Table 1 Model parameters of WJ-8 fastener model
1.2 扣件系统复杂接触关系的模拟
WJ-8 扣件系统各部件间通过一定的接触关系相互配合来保证其正常工作性能。WJ-8 扣件中的接触关系较为复杂,模型中将所有部件间的接触行为离散为法向与切向两类,法向的接触行为通过式(4)定义,认为接触面之间的法向接触力只存在压力,且两者不允许侵入、贯穿;切向则采用简化的库伦摩擦模型。参照既有研究和相关技术条件[15 − 17],模型中需设置的接触对关系见表2。

表2 WJ-8 扣件精细化分析模型接触对设置Table 2 Contact pair of WJ-8 fastener model

式中:P代表接触应力;d代表了接触面间的间隙,正值表示分离,负值表示侵入。
WJ-8 扣件精细化分析模型通过在螺栓道钉顶部施加一定的紧固压力扣紧弹条,使之达到正常工作状态如图2 所示。

图2 WJ-8 扣件精细化模型中扣压力施加方式Fig. 2 Clamping force loading in WJ-8 fastener model
图2所示的扣压力模拟方式既能够再现弹条的紧固过程[18],也方便了后续弹条扣压力及弹程的验证。模型在钢轨端部约束其纵向变形,对绝缘块、轨距挡板等结构约束了其横向变形,在保障计算精度的基础上提高了计算效率。
1.3 模型有效性验证
本节对扣件精细化分析模型的有效性进行验证,以确保模型能够准确反映WJ-8 扣件系统的工作特征。对所建立的扣件分析模型施加安装荷载后,发现弹条位移为14 mm 时,钢轨位移达到0.574 mm,此时换算得到单个弹条扣压力为9.28 kN,弹条与绝缘块间隙为0.42 mm,符合扣件设计要求中单个W1 型弹条扣压力大于9 kN,弹程14 mm,弹条与绝缘块间隙不大于0.5 mm 的规定[17, 19]。
获取扣压力-弹程曲线如图3(a)所示。由图3(a)可知,弹条在14 mm 左右达到“三点接触”状态;“三点接触”状态前后,弹条扣压刚度分别为0.66 kN/mm 和4.90 kN/mm,与文献[15, 20]中W1 型弹条的扣压力-弹程曲线较为吻合。
此外,对钢轨轨头施加垂向荷载,其荷载-位移曲线如图3(b)所示,计算可得此时扣件节点静刚度为31.30 kN/mm,验证了模型的有效性。
2 WJ-8 扣件垂向力学行为分析
2.1 扣件受力阶段分析
提取车辆轨道动力模型计算得到的典型扣件力垂向曲线如图4 所示。
由图4 可知,扣件在受力时可分为受拉阶段和受压阶段,根据作用时间的不同,又可将其过程概括为图5 所示的A、B 两个阶段。
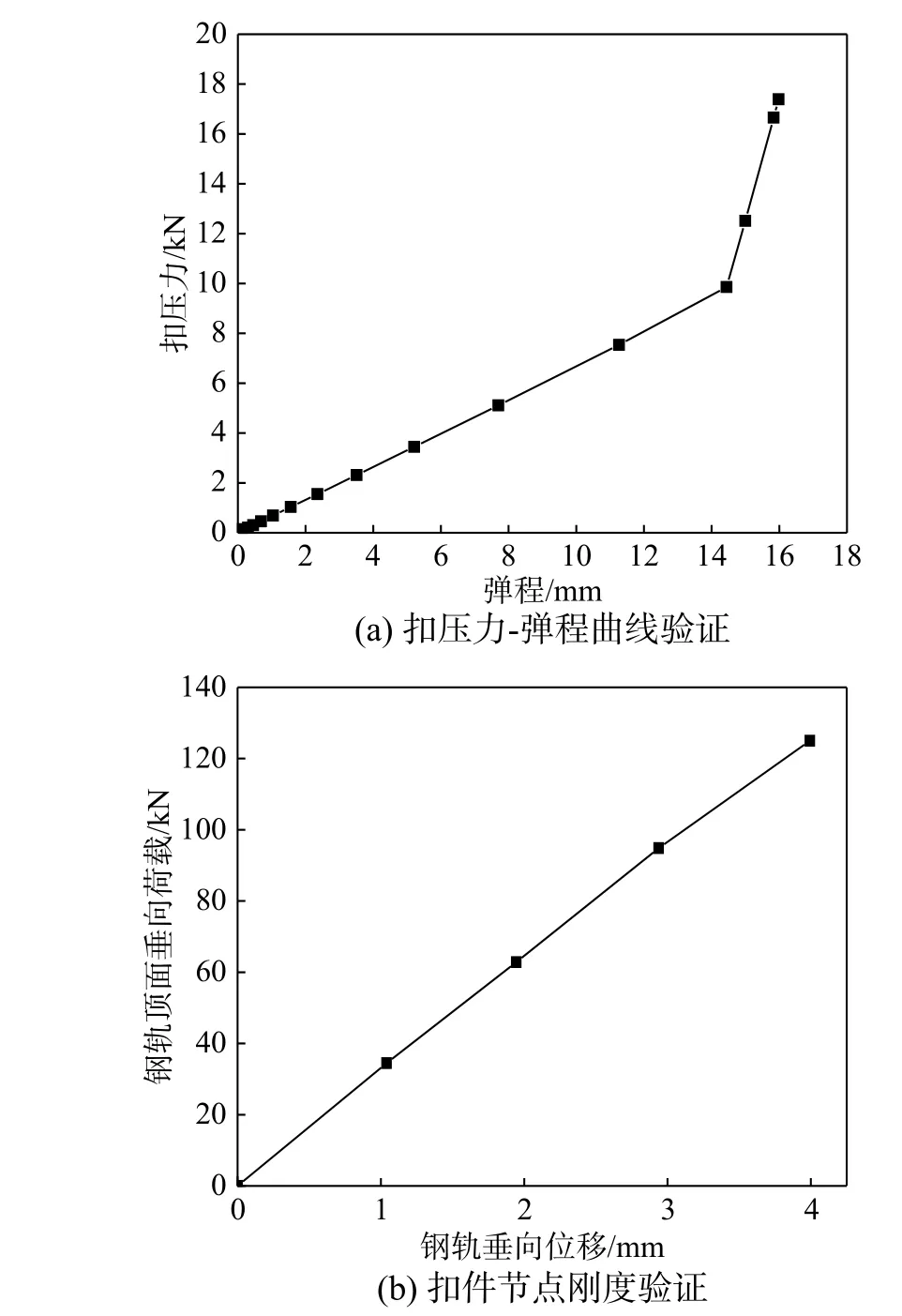
图3 扣件精细化模型有效性验证Fig. 3 Validation of WJ-8 fastener model

图4 典型垂向扣件力时间历程曲线Fig. 4 Typical time history of vertical fastener force
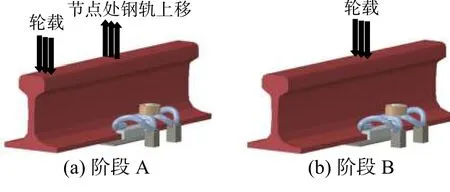
图5 两种典型扣件受力阶段Fig. 5 Two typical loading phase of fasteners
在阶段A 轮载作用于扣件节点之间,在轮载的作用下该处钢轨出现向下的位移,因钢轨自身抗弯刚度,此时扣件节点处有上移的趋势,此时扣件承受拉力[21]。在阶段B 轮载逐步靠近扣件节点位置并作用于节点上方,此时扣件承受压力;而后轮载向前移动,扣件受力又回到阶段A。
当扣件系统正常工作时,扣压件将钢轨固定在承轨台上,使得钢轨具有抵抗上拔力的能力不致出现过大的上移。当扣件扣压件失效后,如扣件弹条断裂飞出,此时扣件的整体抗拉能力将大大减小。
为了量化评价这种限制钢轨向上位移的能力,本文将扣件的抗拉抗压刚度独立开来,并将扣件失效模式分为不失效、扣压力失效和完全失效三类。扣压力失效指扣件弹条断裂或扣压力丧失,此时扣件限制钢轨上移的能力极小,但节点抗压刚度Kc正常;完全失效模式则与文献[2 − 4]类似,轨下垫板已经脱出,钢轨底部无支承。根据扣件不同阶段的受力特征可知,求出扣件系统的整体抗拉刚度Kt,是区分三种失效模式的关键。
2.2 扣件扣压力失效后的垂向非线性行为
为确定扣件整体抗拉刚度Kt,本文利用所建立的扣件精细化分析模型,将上拔力施加在钢轨底面如图6 所示。借鉴静刚度测试方法的思路,加载过程中假定上拔力在钢轨底面均匀分布,加载区域为垫板范围。将扣件抗拉刚度定义为:

式中:F为上拔力;u为钢轨顶面的垂向位移。
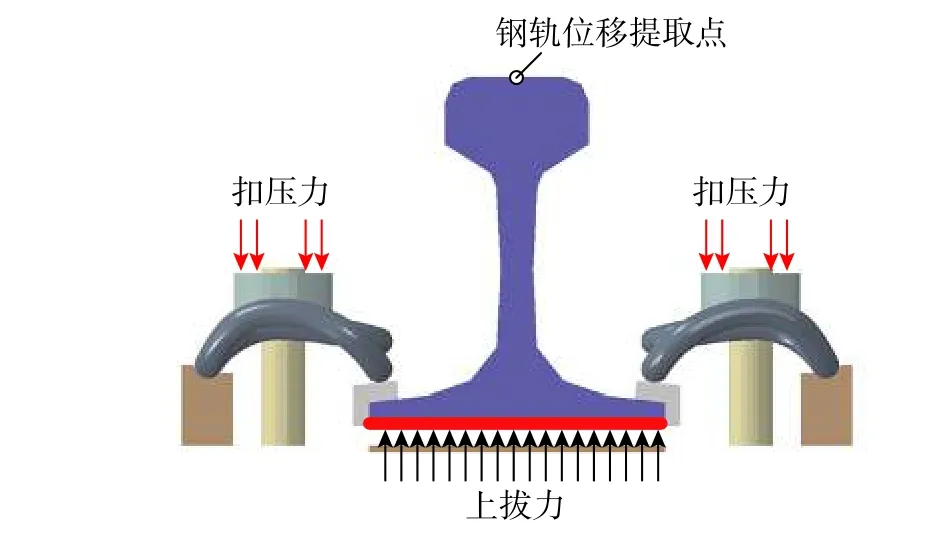
图6 扣件抗拉刚度数值试验加载示意Fig. 6 Loading of numerical test for tensile stiffness of fastener
提取如图6 所示位置的钢轨顶面位移,获取上拔力-位移曲线如图7 所示。
当弹条扣压力未损失时,两根弹条所提供的扣压力Fc为18 kN。由图7 可知,上拔力-位移曲线存在明显的双线性特征,当上拔力为18 kN时,钢轨向上的垂向位移为0.54 mm,此时、Kt为33 kN/mm,与扣件节点抗压刚度Kc相差不大;当上拔力超过18 kN 后,上拔力-位移曲线出现了明显的“屈服”阶段,上拔力超过22 kN 时,Kt显著降低,约为0.44 kN/mm,对钢轨上移基本无约束作用。
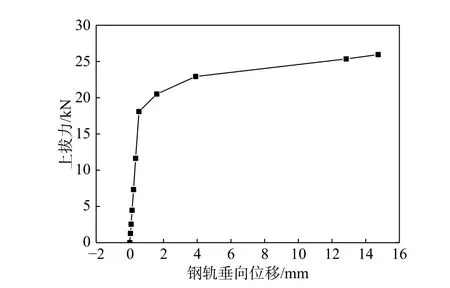
图7 WJ-8 扣件上拔力-位移曲线Fig. 7 Uplift force-displacement curve of WJ-8 fastener
为探究Kt出现这种“屈服”现象的原因,提取弹条塑性应变峰值与对应钢轨垂向位移的关系曲线如图8 所示。由图8 可知,塑性应变-位移曲线与上拔力-位移曲线趋势基本一致,出现了明显的双线性特征。其塑性应变的发展特征与弹条在上拔过程的变形特征息息相关。如图9 所示,当上拔力未超过18 kN 时,弹条中肢存在的残余扣压力使得弹条对钢轨仍有较好的限制能力,并使得中肢与弹条前肢的相对位移逐渐增大,中肢与前肢间存在的非协调变形使得尾肢中部塑性应变迅速增长。
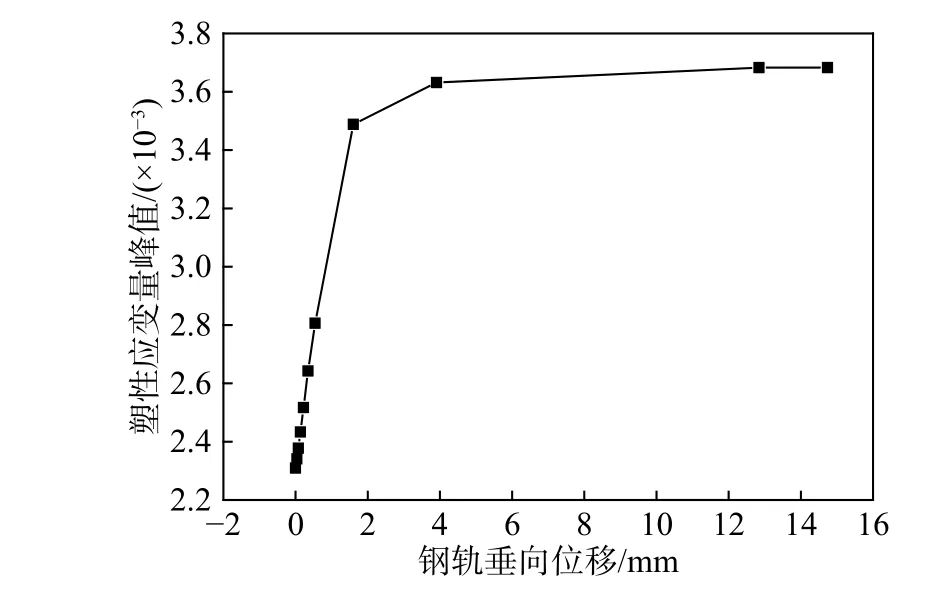
图8 WJ-8 扣件塑性应变量峰值-位移曲线Fig. 8 Peak plastic strain-displacement curve of WJ-8 fastener
此外,此时弹条与绝缘块间一直处于“三点接触”状态,传力关系较先前发生了改变,弹条处于偏心受力的状态,故此时的Kt较先前的弹条前端扣压刚度稍低。当上拔力增长至两根弹条提供的扣压力时,此时弹条变形趋势转为整体外翻,对钢轨的限位能力大大减弱,其塑性应变也不再发展。
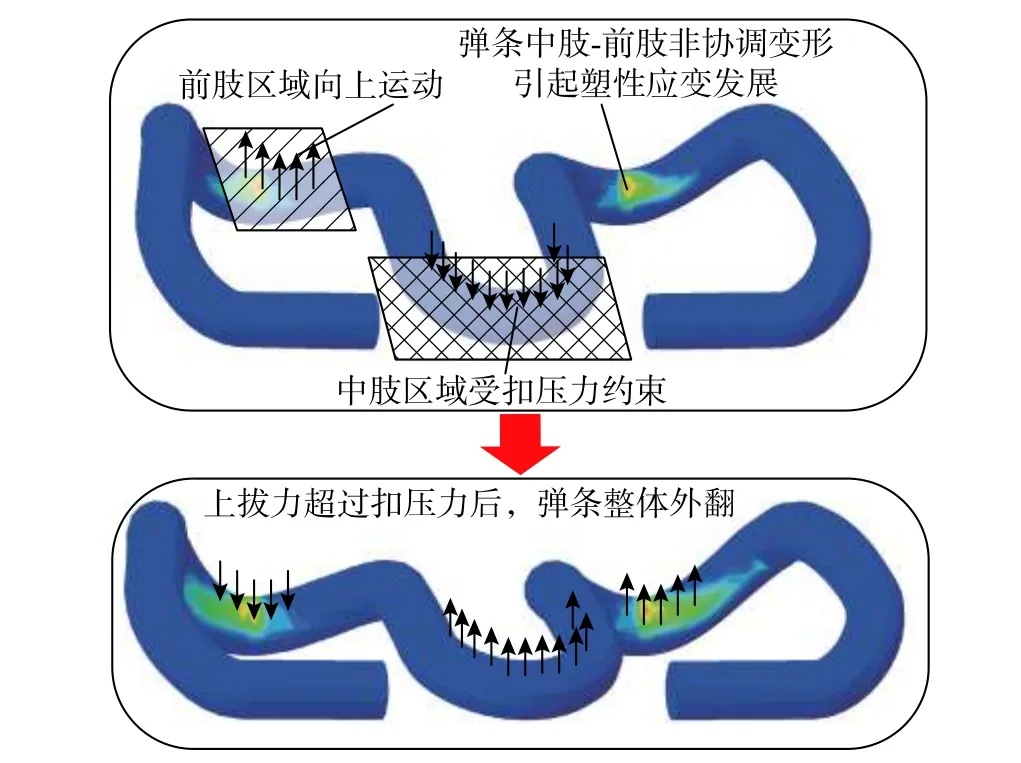
图9 WJ-8 扣件双线性上拔刚度发生机理Fig. 9 Mechanism of bilinear uplift stiffness of WJ-8 fastener
为明确弹条扣压力损失对扣件整体抗拉刚度Kt的影响,分别考虑扣压力损失25%、50%和75%的情况,采用相同的加载方式,获取不同扣压力下的上拔力-位移曲线如图10 所示。

图10 不同扣压力条件下上拔力-位移曲线Fig. 10 Uplift force-displacement curve under different clamping force
由图10 可知,当扣压力出现损失后,上拔力-位移曲线更早地到达“屈服”阶段,即扣压力的损失使得Kt更快到达低刚度阶段。当弹条扣压力只剩原来的50%时,上拔力达到9 kN 后曲线就出现拐点。
2.3 扣件扣压力失效在车辆-轨道耦合模型中的简化表达
既有的车辆轨道动力学模型采用弹簧-阻尼单元模拟扣件的垂向刚度行为时,将其简化为如图11(a)所示的线性刚度弹簧[22 − 23],即假定扣件的抗拉刚度与受压刚度一致。本文在传统线性刚度弹簧的基础上进行改进,基于扣件精细化模型的结果对扣件垂向非线性刚度行为[24 − 25]进行修正。
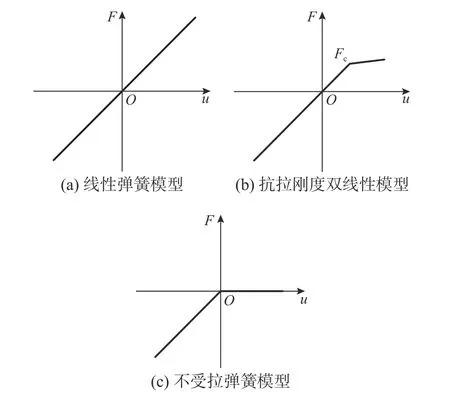
图11 不同扣件垂向刚度模型Fig. 11 Different vertical stiffness models of fasteners
由2.3 节可知,扣件的抗拉刚度存在非线性特征。基于此,本文提出了如图11(b)所示的抗拉刚度双线性模型。在抗拉刚度双线性模型中,当扣件承受压力时,此时扣件弹簧刚度与节点抗压刚度Kc一致(即F<0,K=Kc);当扣件弹簧转入受拉状态,但所承受的上拔力未超过扣压力,此时可认为扣件抗拉刚度与节点刚度一致(即Fc>F>0,K=Kt=Kc);当上拔力超过了扣件的扣压力后,认为扣件限制钢轨上移的能力基本消失,此时设置弹簧的抗拉刚度为0(即F>Fc,K=Kt=0)。
当扣件扣压力全部失效时,在抗拉刚度双线性模型的基础上本文还提出了如图11(c)所示的不受拉弹簧模型,扣件弹簧不提供抗拉刚度(即F>0,K=Kt=0)。
3 不同扣件失效类型对车轨动力系统的影响研究
3.1 车辆-轨道耦合动力模型
为评估不同扣件失效类型对车轨动力响应特性的影响,本文基于多体动力学理论和有限元方法建立了车辆-轨道耦合动力模型(见图12),并通过ABAQUS 软件将其实现。将车辆视为由车体、转向架及轮对组成的多刚体系统,转向架-轮对、车体-转向架间采用三向弹簧-阻尼单元模拟一系、二系悬挂。模型分别考虑车体、转向架6 个自由度,轮对5 个自由度共计38 个自由度。车辆采用CRH3型车,建模参数参见文献[26]。
轨道模型选取CRTSⅢ型板式无砟轨道,包括钢轨、扣件、轨道板、自密实混凝土层、底座板。钢轨及下部轨道结构均采用实体单元进行建模,将轨道板与自密实混凝土共节点建模以表征其黏结关系良好;自密实混凝土层与底座间存在土工隔离层,建模时通过接触单元模拟,切向考虑为一定的摩擦作用;底座上设置两个尺寸为0.6 m×0.4 m 的凹槽,凹槽四周设有弹性垫层,建模时考虑为线性接触刚度[27]。扣件仍然考虑为多根三向弹簧-阻尼单元[28]。扣件垂横向刚度分别取30 kN/mm及25 kN/mm[20],纵向阻力取15 kN/组。当涉及到不受拉弹簧时,将弹簧垂向设置为仅受压的模式。CRTSⅢ型板式无砟轨道其他具体参数参见文献[29]。
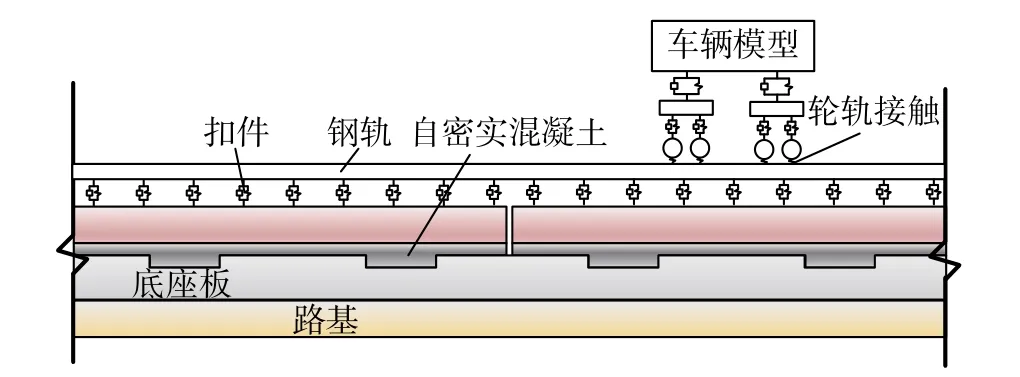
图12 车辆-轨道耦合动力模型Fig. 12 Vehicle-track coupling dynamic model
建立轮轨接触时将其离散为法向与切向的接触行为,法向接触力采用如式(7)所示的赫兹非线性理论进行计算如式所示;切向则采用简化的库伦摩擦模型,摩擦系数取为0.3。模型通过罚函数法将法向、切向接触条件引入泛函方程中进行求解。轮轨随机不平顺与文献一致,采用《高速铁路无砟轨道不平顺谱》推荐的随机不平顺,波长范围取2 m~200 m。模型总长度为120 m。

式中:G/(m/N2/3)表示轮轨接触常数; δZ(t)表示轮轨间的弹性压缩量;t表示时间。本文采用磨耗型车轮踏面,轮轨常数G采用下式进行计算。
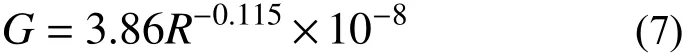
式中,R表示车轮滚动圆半径
3.2 扣件扣压力失效与完全失效对车辆轨道系统动态响应的影响
本节主要分析了扣件不同失效模式对车辆轨道系统动态响应的影响。分析前首先基于双线性抗拉刚度弹簧模型建立了正常状态的扣件,扣件提供的扣压力(Fc=18 kN),并与线性刚度弹簧模型的计算结果进行了对比如图13 所示。
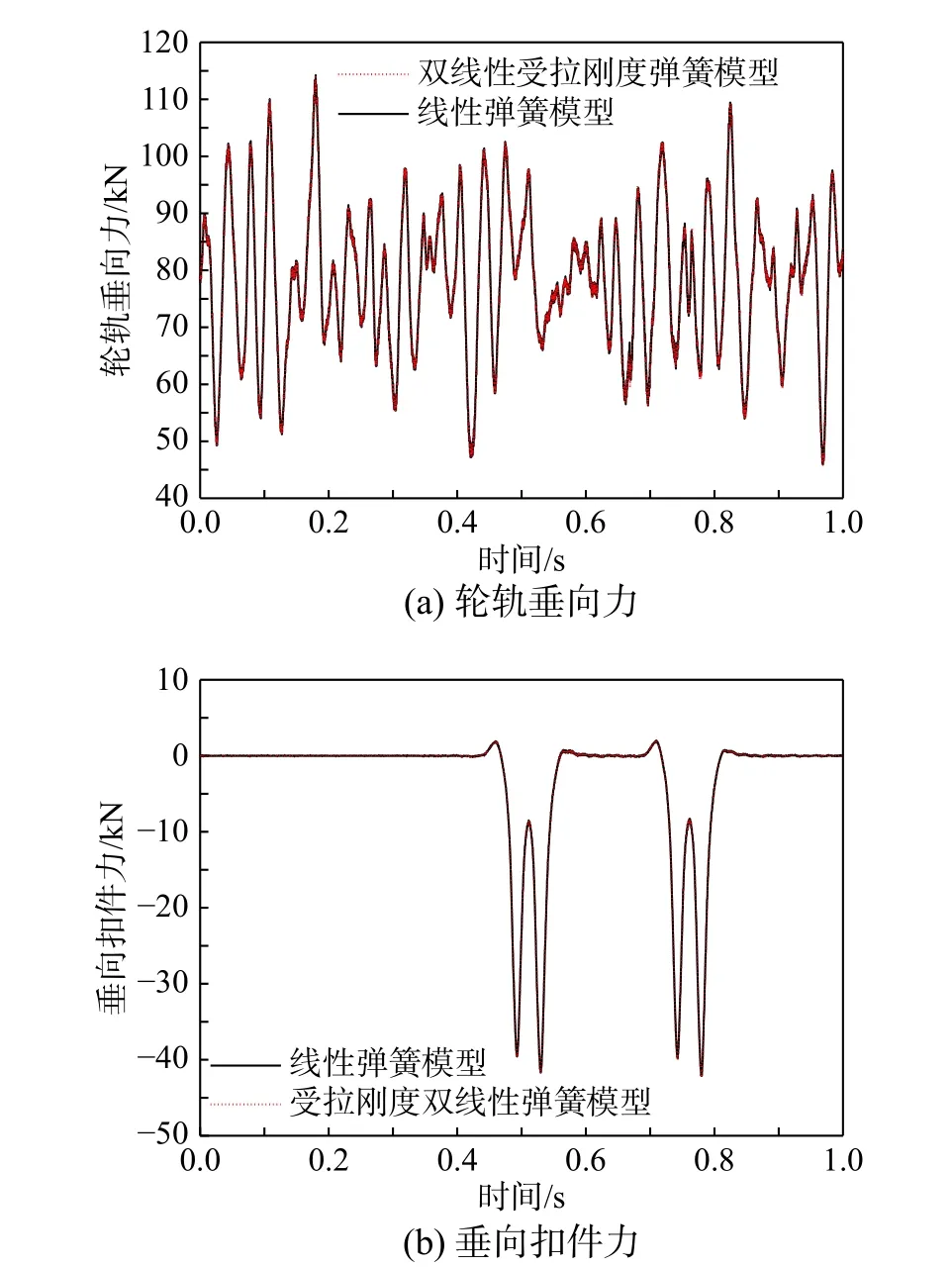
图13 线性刚度弹簧模型与双线性抗拉刚度弹簧模型动力响应对比Fig. 13 Comparison of dynamic response of linear stiffness spring model and bilinear tension stiffness spring model
由图13 可知,扣件在正常工作状态下,线性刚度弹簧模型与双线性抗拉刚度弹簧模型的结果基本无差异,这是因为在车辆行驶过程中扣件弹簧单元所承受的上拔力并未超过扣件的扣压力,扣件仍能提供较好的抗拔刚度。这也说明在进行动力学建模时,如不考虑扣件病害,将其简化为线性刚度弹簧也是合理的。
考虑到扣件在实际中所受上拔力大约在1 kN~4 kN,相当于扣压力损失77.8%~94.4%后扣件系统才有可能在车辆荷载影响下进入弱刚度阶段。这时扣件的工作状态已经接近弹条断裂完全损失扣压力的情况。因此在具体分析时,本文只考虑扣压力失效和完全失效两种扣件失效类型。扣压力失效时扣件弹条已经断裂,扣压力已完全损失,但垫板仍处于原位提供抗压刚度,模型中采用了不受拉弹簧模型来模拟失效扣件;模拟完全失效时与既有研究[1 − 5, 23]类似,将失效扣件调整为无刚度的弹簧。高速铁路现场调研情况表明,扣件弹条伤损区段相对集中且连续出现,且大多集中在一股钢轨上。因此设置计算工况时综合既有研究及现场情况,同时便于区分、放大不同失效类型的具体影响,设置了五个扣件连续失效的场景如图14 所示。
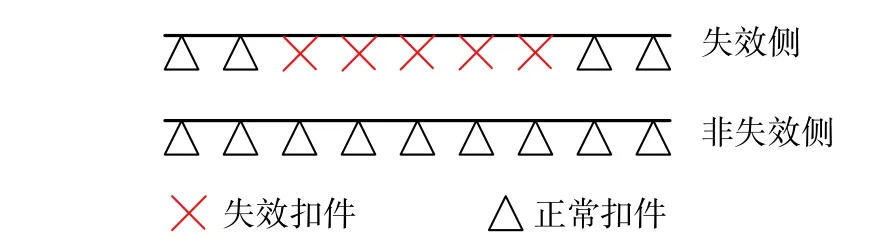
图14 扣件失效计算工况设置Fig. 14 Fastener failure calculation conditions
以车辆运行速度250 km/h 为例,对比不同扣件失效类型与正常线路的动力响应时如图15 所示。
图15(a)为CRH3 型车第一轮对在失效侧和非失效侧的轮轨垂向力。由图15(a)可知,扣件扣压力失效情况下,由于轨下仍存在支承效应,轮轨垂向力与正常线路相比无明显差异。但扣件完全失效后对轮轨力的影响更为显著。具体而言,在进入扣件失效区域时,由于轨下刚度锐减,失效侧轮轨力首先发生减载,而后出现较为剧烈的波动。扣件完全失效后,轮轨力最大可达181 kN,最小值已接近0 kN,轮重减载率已远远超过安全限值。由图15(b)可知,相对失效侧,对侧的轮轨力差异较小,扣件失效对轮轨动态行为的影响主要集中在失效侧。
图15(c)和图15(d)分别显示了失效侧和非失效侧的垂向扣件力。由图15(c)可知,扣件扣压力失效时,失效侧扣件垂向力峰值无明显变化,但放大扣件力曲线可知,弹条断裂后扣件系统已经不再承受钢轨带来的上拔力。图15(d)结果表明,扣压力失效时非失效侧扣件力无明显变化,但扣件完全失效后,非失效侧扣件力最大值由35.74 kN增加至46.32 kN,增加了29.60%。
图15(e)给出了失效侧钢轨的垂向位移时程曲线。由图15(e)可知,扣件扣压力失效时钢轨垂向位移峰值变化不大。但放大扣件位移曲线后发现,弹条断裂后扣件无法约束钢轨的上翘变形,使得钢轨的上翘位移有所增加。而扣件完全失效后,钢轨下无支承,失效区域线路的抗弯刚度全来自于钢轨自身,此时钢轨垂向位移峰值由正常工况的1.31 mm 增长至12.35 mm,增加了近九倍。对侧的钢轨位移区别不大,在此不再列出。

图15 不同扣件失效类型与正常线路的动力响应时程曲线Fig. 15 Time history of dynamic response of different fastener failures and normal lines
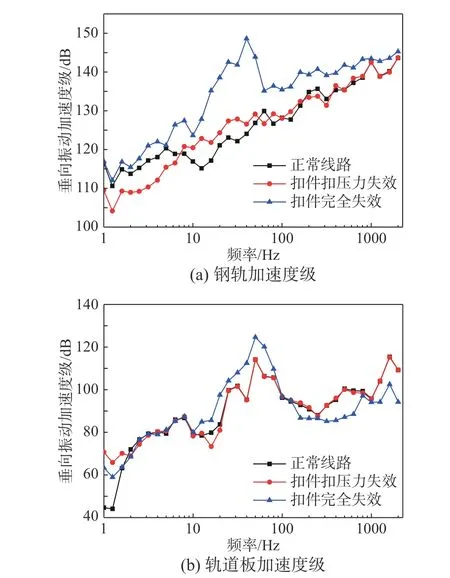
图16 轨道1/3 倍频程加速度级Fig. 16 1/3 octave band acceleration level of track structure
图16 给出了钢轨、轨道板振动加速度的1/3 倍频程。扣件扣压力失效和完全失效都削弱了失效区域内的钢轨约束,结构振动特性发生了明显改变。从图中可知与正常线路相比,扣件处于扣压力失效状态时,钢轨加速度在8 Hz~50 Hz 中心频段范围内有所增长,这种增长主要来自钢轨的上翘位移。在800 Hz 中心以后,振动加速度基本无明显差异。扣件扣压力失效对轨道板的振动特性未产生明显影响。
扣件完全失效时钢轨加速度在全频段都有所增加,其中在10 Hz~125 Hz 中心频段范围内出现了明显的增长,覆盖了当前时速下波长为单个扣件间距和6 个扣件间距时所对应的频率。扣件完全失效后,由于钢轨振型的影响,峰值频率出现在中心频率45 Hz 处。轨道板振动加速度也出现了全频段的放大,但变化程度相对钢轨较小。
4 结论
本文针对扣件失效在动力学模型中的模拟问题,通过建立扣件精细化分析模型,将WJ-8 扣件垂向力学行为分阶段离散,提出了由节点抗压刚度和抗拉刚度组成的简化扣件模型,并基于弹条的变形姿态及塑性应变量解释了扣件在承受上拔力时的非线性力学行为。在此基础上通过车轨动力模型比较了不同扣件失效类型对车轨系统动态响应的影响。主要结论总结如下:
(1)扣件系统的受力过程可分为受压和受拉两个阶段。扣件抗拉刚度存在双线性特征,通过弹条塑性应变量和运动姿态解释了弹条出现双线性抗拉刚度的原因。扣压力的丧失使得扣件抗拉刚度更快到达低刚度阶段。
(2)在原有线弹性弹簧模型的基础上提出了改进的抗拉刚度双线性模型和不受拉弹簧模型用以表征车辆轨道耦合动力学模型中处于不同状态的扣件。相较既有研究优化了在扣件扣压效应模拟方面的建模。
(3)扣件扣压力失效和完全失效都减弱了扣件对钢轨的约束性能。扣件失效对轮轨动态行为的影响主要集中在失效侧。扣件扣压力失效对行车安全性无显著影响,但钢轨在车辆行经前的上翘位移有所增长;钢轨加速度也在低频范围内增大,主要集中在在8 Hz~50 Hz 中心频段范围内,高频区段区别不大。扣件扣压力失效对轨道板的振动特性未产生明显影响。
(4)相较于扣件扣压力失效模式,完全失效对车轨系统的影响更大,具体表现为各个动力响应指标的显著增大。车辆进入完全失效区域时,轨下刚度的锐减使得失效侧轮轨力出现大幅度减载随后剧烈波动。根据分析结果可知,钢轨发生五个扣件完全失效时,轮轨减载率峰值远远超过安全限值,已经对行车安全造成了影响,需要引起重视。
