教学考试杂志社“优师计划”阶段性成果展示——“动力学”相关试题选登

一、相对运动

【例1】如图所示，在地面上固定一斜面，现将物块P、Q叠放在一起置于斜面上，整体沿着斜面下滑，下列说法正确的是

( )

A.若整体匀速下滑，物块Q受到三个力的作用

B.若整体加速下滑，物块P对物块Q的摩擦力水平向右

C.若整体加速下滑，物块Q处于失重状态

D.若整体加速下滑，物块Q处于超重状态

【答案】C

【解析】若整体匀速下滑，物块Q处于二力平衡状态，A错误；若整体加速下滑，说明两者的加速度都是沿着斜面向下，该加速度具有水平向左的分量和竖直向下的分量，因此P对Q的摩擦力水平向左，物块Q处于失重状态，C正确，BD错误。

【例2】如图所示，水平传送带的质量M=9 kg，两端点A、B间距离L=4 m，传送带以加速度a=2 m/s2由静止开始顺时针加速运转的同时，将一质量为m=1 kg的滑块(可视为质点)无初速度地轻放在A点处，已知滑块与传送带间的动摩擦因数为0.1，g取10 m/s2，电动机的内阻不计。传送带加速到v=2 m/s的速度时立即开始做匀速转动，而后速率将始终保持不变，则滑块从A运动到B的过程中

( )

A．系统产生的热量为1 J

B．滑块机械能的增加量为3 J

C．滑块与传送带相对运动的时间是3 s

D．传送滑块过程中电动机输出的电能为5 J

【答案】A

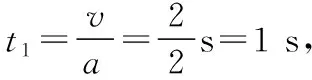
【例3】如图，质量M=0.3 kg的长方体钢板静止在粗糙的水平面上，质量m=0.5 kg的滑块静止在钢板右端。一质量m0=0.2 kg的光滑小球沿水平面以初速度v0=5 m/s向右运动，与钢板发生弹性正碰，碰撞时间极短，碰撞后钢板向右滑行，滑块恰好不从钢板上掉下来。已知钢板与水平面间的动摩擦因数μ1=0.1，与滑块间的动摩擦因数μ2=0.2，取g=10 m/s2。求：

(1)碰撞后瞬间，小球的速度大小和钢板的速度大小；

(2)滑块在钢板上滑行的时间t；

(3)钢板的长度L以及钢板刚停下时滑块与小球间的距离x。

【解析】(1)碰后瞬间，设小球的速度为v，钢板的速度为v1，小球与钢板发生弹性正碰，满足动量守恒和机械能守恒，则

m0v0=m0v+Mv1

小球的速度大小为1 m/s，钢板的速度大小为4 m/s

(2)碰后，滑块水平向右做匀加速直线运动，钢板水平向右做匀减速直线运动，直至与滑块的速度相同。设钢板、滑块运动的加速度大小分别为a1、a2，根据牛顿第二定律有

μ2mg=ma2

钢板与滑块速度相同时有

v1-a1t1=v2=a2t1

解得t1=0.5 s

十几天后，西大街那孩子王钓鱼，不想失了足，掉入河里，偏他不会水，头冒了两下，就沉下去了。跟他一起来的孩子都慌了，没一个敢去救他。

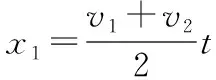
钢板的长度L=x1-x2

解得L=1 m

设钢板与滑块共速后到刚停下所用的时间为t2，则

钢板刚停下时滑块与小球间的距离

解得x=2.25 m

【例4】如图所示,质量为M=6 kg的长木板放在光滑水平地面上,在长木板的最右端和距右端 4 m 的P点处各放一物块B和A(均可视为质点)，物块A的质量为m1=2 kg,物块B的质量为m2=1 kg,长木板P点左侧足够长，长木板上表面P点右侧光滑，P点左侧(包括P点)粗糙，物块A与长木板间的动摩擦因数μ=0.5,现用一水平向右的恒力F作用于长木板上,使长木板由静止开始运动,设物块A与木板间的最大静摩擦力等于滑动摩擦力,g=10 m/s2，求：

(1)当长木板由静止开始运动时，若要物块A与长木板保持相对静止，拉力F满足的条件；

(2)若拉力F=36 N,在物块A、B相碰时撤去拉力F,物块A与B发生弹性碰撞，碰撞之后物块A的速度v1和物块B的速度v2。

【解析】(1)当A与长木板间的摩擦力达到最大静摩擦力时将要发生相对滑动，设此时物块A的加速度为a0，以A为研究对象，根据牛顿第二定律

μm1g=m1a0

因为B与长木板间没有摩擦力，以长木板和物块A整体为研究对象,根据牛顿第二定律，当A与长木板间将要发生相对滑动时F0=(M+m1)a0

联立解得F0=40 N

所以若要物块A与长木板保持相对静止，拉力

F<40 N

(2)当拉力F=36 N时小于40 N,开始时物块B保持静止，物块A与长木板一起加速

解得v0=6 m/s

物块A、B发生弹性碰撞，根据动量守恒定律

m1v0=m1v1+m2v2

根据机械能守恒定律

两式联立解得v1=2 m/s

v2=8 m/s

二、功能关系

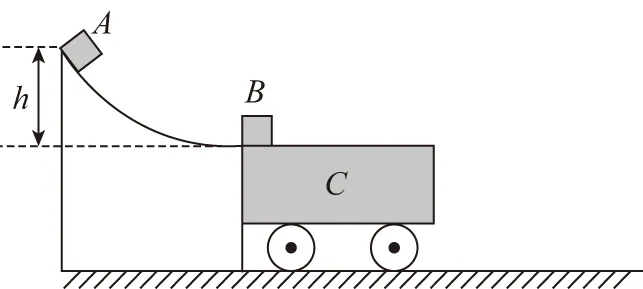
【例1】如图所示，轻弹簧的一端固定在质量为2m的滑块A上，质量为2m的光滑弧形滑槽B静止放在光滑水平面上，弧形滑槽底端与水平面相切，一个质量为m的小物块C从滑槽高h处开始自由下滑，下列说法正确的是

( )

A．滑块在整个运动过程中，A、B、C系统机械能守恒

D．物块反弹后追不上滑槽

【答案】CD

【例2】如图所示，光滑水平地面上有一上表面粗糙且水平、质量为mC=10 kg的小车C。小车C与一固定在地面上的光滑圆弧底端等高且平滑相接。将质量为mB=2 kg的滑块B置于小车C的最左端。现有一质量为mA=3 kg的滑块A从距离小车的水平面高度为h=1.25 m处的光滑轨道由静止下滑。滑块A与B碰撞后立即粘在一起运动，最终没有滑落小车。整个过程中滑块A和B都可以视为质点。滑块A和B与小车C之间的动摩擦因数均为μ=0.2，取g=10 m/s2，求：

(1)滑块A和B粘在一起后和小车C相对运动过程中各自加速度的大小？

(2)若从A、B碰撞时开始计时，则0～3 s时间内，滑块A、B与小车C因摩擦产生的热量Q为多少？

【解析】(1)滑块A和B粘在一起后，滑块A、B和小车C都向右运动，设它们的加速度分别为a1和a2

由牛顿第二定律可得

滑块AB-μ(mA+mB)g=(mA+mB)a1

a1=-2 m/s2

小车Cμ(mA+mB)g=mCa2

a2=1 m/s2

(2)设滑块A滑到圆弧底端时的速度为vA

由机械能守恒定律可得

设A、B碰撞后的共同速度为vAB，由动量守恒定律可得

mAvA=(mA+mB)vAB

设在0～3 s时间内，滑块A、B与小车C相对运动时间为t，由相对静止时速度相等可得

vAB+a1t=a2t

解得t=1 s

即1 s后物块和小车相对静止向右匀速直线运动

设在相对运动时间t内滑块A、B和小车C的位移分别为x1和x2，由匀变速直线运动规律可得

设滑块A、B与小车C相对运动的位移为Δx，则有

Δx=x1-x2

0～3 s时间内，滑块A、B与小车C因摩擦产生的热量

Q=μ(mA+mB)g·Δx

联立解得Q=15 J

【例3】如图甲所示,质量为0.3 kg的物块，静止在水平面上，不计空气阻力，在竖直向上的拉力F的作用下，由静止开始上升了9 m，此过程中，拉力做的功W和物块上升高度x之间的关系如图乙所示，g=10 m/s2。下列说法中正确的是

( )

B.此过程中，物块的机械能增加了42 J

C.上升高度x=9 m时，物块速度恰好为零

D.上升9 m后，若保持拉力不变，物块回到地面时动能为18 J

【答案】AC

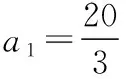
【例4】2018年10月23日港珠澳大桥正式通车。港珠澳大桥海底隧道沉管长5 664米，由33节巨型沉管和1个“最终接头”对接而成，“最终接头”是一个重约为6 000吨的巨大钢筋混凝土结构，将“最终接头”简化为一长方体模型，简化结构和吊装示意图如图所示。

(1)“最终接头”在这艘世界最大单臂全旋回起重船“振华30”两个吊钩、八根吊缆的巨大牵引力下，缓慢到达沉放海域上空，如果“最终接头”重量为G，每根吊缆与竖直线的夹角为θ，求每根吊缆的牵引力FT；

(2)当“最终接头”底边开始没入水面，始终以微小的平面误差缓慢下沉至28米深的海底，最终与沉管E29和E30对接成功，港珠澳大桥海底隧道顺利合龙。设当地海水的密度为ρ，“最终接头”长方体模型长为L，高为h，宽为d，求“最终接头”下沉至海底H处对接过程中，浮力对“最终接头”做的功W。

【解析】(1)根据对称性和平衡条件得8FTcosθ=G

(2)“最终接头”长方体受到的浮力分两个阶段，第一阶段是从水面到完全浸没，浮力F1是变力，第二阶段从完全浸没到下沉到海底，浮力F2是恒力。

第一阶段：F1=ρVg

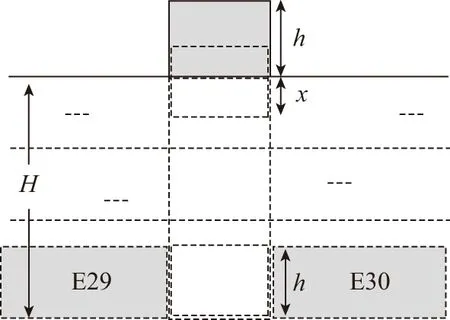
设长方体从海面下沉位移为x，即V=Ldx

联立解得F1=ρgLdx

可知浮力与位移成正比

从水面到完全浸没，浮力对“最终接头”做的功

第二阶段从完全浸没到下沉到海底

则F2=ρgLdh

浮力对“最终接头”做的功

W1=F2×(H-h)=ρgLdh(H-h)

故“最终接头”下沉至海底H处对接过程中，浮力对“最终接头”做的功

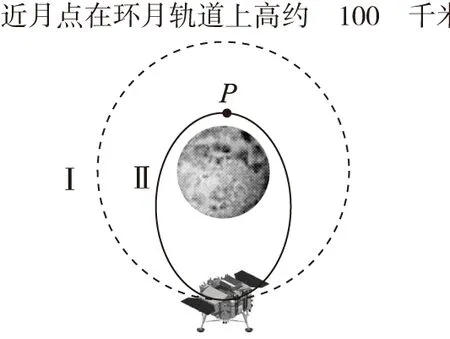
【例5】2018年12月30日，发动机对绕月圆轨道Ⅰ的“嫦娥四号”做功W进行减速变轨，进入椭圆形轨道Ⅱ，如图所示。2019年 1月3日“嫦娥四号”在近月点P以速度v开始第二阶段减速，进行登月任务。已知在轨道Ⅰ时“嫦娥四号”的总能量为E，“嫦娥四号”的质量为m,忽略其他天体的影响，把无穷远处作为月球引力势能的零势能点,则在近月点月球对“嫦娥四号”的引力势能大小为

( )

【答案】D

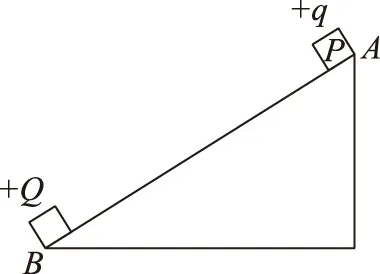
【例6】如图所示，绝缘粗糙斜面体固定在水平地面上，一带电荷量为+q的物块P放置于斜面体上的A点，斜面体的底端点固定一个带电荷量为+Q的物块。现让带电物块P从A点静止释放，物块P第一次沿斜面向下运动到M点时加速度为零，然后继续下滑到N点速度为零后沿斜面向上运动(M点与N点图中未标出，物块可视为质点)，则关于物块P以下说法正确的是

( )

A．从A点运动到N点的过程中，机械能变化量等于摩擦力和库仑力做功之和

B．从A点运动到N点的过程中，电势能的增加量等于重力势能减少量和摩擦产生的热量之和

C．第一次下滑过程中加速度为零的位置一定在第一次返回过程中加速度为零的位置上方

D．只能停在第一次下滑过程中加速度为零的位置和在第一次返回过程中加速度为零的位置之间(含这两个位置)

【答案】ACD

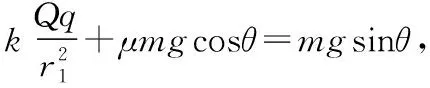
三、杆绳模型

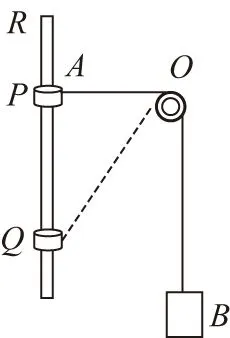
【例1】中间有光滑圆孔的圆环A与物块B用一根不可伸长的轻绳连接，A套在竖直光滑的细杆上，细杆的上端为R，绳绕过定滑轮将B竖直悬挂，如图所示，轻绳与定滑轮间无摩擦。让圆环A从与O等高的P点由静止释放，下落到Q点时速度恰好为零，此时B没有碰到滑轮，已知OP=0.3 m，PR=0.225 m，PQ=0.4 m，重力加速度g=10 m/s2。则

( )

A．圆环A和物块B的质量之比为3∶4

B．当圆环A的速度最大时，A、B的速度之比为2∶1

C．圆环A和物块B的机械能之和始终保持不变

D．若圆环A以3 m/s的初速度从Q点向上滑动，圆环A不能滑出细杆顶端

【答案】BC

( )

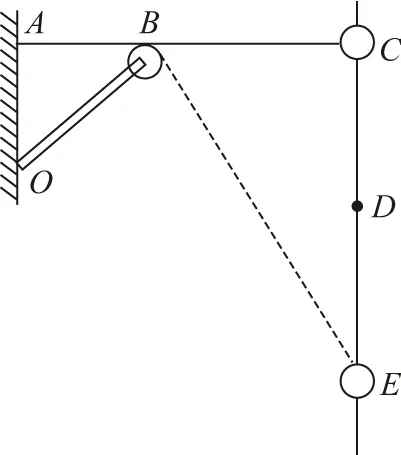
A．小球在D点时速度最大

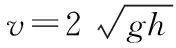
C．小球在CD阶段损失的机械能等于小球在DE阶段损失的机械能

D．若O点没有固定，杆OB在绳的作用下以O为轴转动，在绳与B点分离之前，B的线速度等于小球的速度沿绳方向分量

【答案】AD

【例3】有一轻杆固定于竖直墙壁上的O点，另一端A固定一轻滑轮，一足够长的细绳一端挂一质量为m的物体，跨过定滑轮后另一端固定于竖直墙壁上的B点，初始时物体处于静止状态，O、B两点间的距离等于A、B两点间的距离，设AB与竖直墙壁的夹角为θ，不计滑轮与细绳的摩擦,下列说法正确的是

( )

A.系统平衡时杆对滑轮的力一定沿杆的方向

B.若增大杆长OA，O与B位置不变且保持OB=AB,使角θ增大,则杆对滑轮弹力的方向将偏离OA杆

C.若保持A点的位置不变，将绳子的固定点B点向上移动，则杆对滑轮的弹力变大

D.若保持AB与竖直墙壁的夹角θ不变，将轻杆的固定点O向下移动，则杆对滑轮弹力的方向不变

【答案】AD

【解析】绳子上的弹力大小等于物体的重力mg，则绳子对滑轮的两弹力的合力方向在两弹力的角平分线上，根据平衡条件可得杆对滑轮的弹力方向也在角平分线上，O、B两点间的距离等于A、B两点间的距离，根据几何关系可得，杆OA恰好在两弹力的角平线方向上，故A正确；若保持O、B两点位置不变，增大杆长OA,使AB与竖直墙壁的夹角θ增大,仍保持O、B两点间的距离等于A、B两点间的距离，杆OA仍在两弹力的角平分线上，杆对滑轮的弹力仍沿杆方向，故B错误；若保持A点的位置不变，将绳子的固定点B向上移动，绳子对滑轮的两力夹角变大，合力变小，滑轮处于平衡状态，则杆对滑轮的弹力变小，故C错误；若保持AB与竖直墙壁的夹角θ不变，将轻杆的固定点O向下移动，两绳对滑轮的弹力大小方向都不变，则杆对滑轮的力仍在两绳弹力的角平分线上，所以杆对滑轮弹力的方向不变，故 D正确。

【例4】如图甲的长江索道被誉为“万里长江第一条空中走廊”。索道简化示意图如图乙所示，索道倾角为30°，质量为m的车厢通过悬臂固定,悬挂在承载索上，在牵引索的牵引下一起斜向上运动。若测试运行过程中悬臂和车厢始终处于竖直方向，缆车开始以加速度a1=10 m/s2向上加速，最后以加速度a1=10 m/s2向上减速，重力加速度大小为g=10 m/s2，则向上加速阶段和向上减速阶段悬臂对车厢的作用力之比为

( )

甲

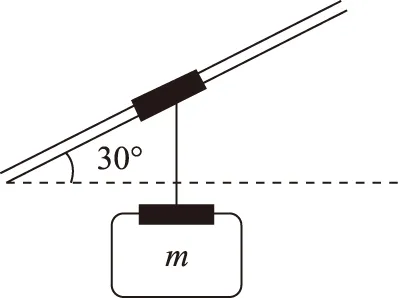
乙

C.2∶1 D.1∶2

【答案】A