浅析高中物理中的弹簧问题
2020-11-13江西范云龙
江西 范云龙
纵观历年各省的高考试题和各地的模拟试题,弹簧问题无疑是其中的一大热点题型,而且弹簧问题也是学生学习中的一大难点。此类试题往往将弹簧模型与力、运动、能量等内容结合,有较强的综合性,能考查学生的思维能力、分析综合能力等,对学生的要求较高。本文结合一些典型例题对弹簧问题的几个常见类型进行剖析,分析解题思路,归纳研究方法,以飨读者。
一、“轻弹簧”问题
高中阶段所涉及的弹簧模型大多都会说明不考虑其质量,我们把这种弹簧称为“轻弹簧”或“轻质弹簧”。“轻弹簧”模型是一种非常常见的理想化物理模型。由于“轻弹簧”的质量忽略不计,任意选取一小段弹簧,其两端所受张力一定平衡,否则根据牛顿第二定律,这段弹簧的加速度会无限大,不符合一般的题设情境。故任一“轻弹簧”中各部分间的张力应处处相等,均等于弹簧两端受到的力,并且弹簧一端受力为F时,另一端受力一定也为F,若使用弹簧测力计测量,则其示数为F。
【例1】如图1所示,弹簧测力计放在光滑水平面上,其外壳质量为m,弹簧及挂钩质量忽略不计,在弹簧测力计挂钩上施加水平向右的力F1,同时在其外壳上施加水平向左的力F2,且F1>F2,则弹簧测力计的加速度大小为________,弹簧测力计的读数为________。

图1

【说明】F2作用在弹簧测力计外壳的外部,并没有作用在弹簧的左端,弹簧左端受到的力是由外壳内部施加的。
【点评】本题以弹簧测力计为研究对象,需要学生准确分析受力情况。题中弹簧测力计外壳质量为m,而弹簧及挂钩质量忽略不计,这就是典型的“轻弹簧”问题。在分析受力时要注意“轻弹簧”两端受力一定大小相等,方向相反,大小均为F1,即弹簧测力计的读数为F1,然后再对整个弹簧测力计进行受力分析,计算出其受到的合力大小,进而算出加速度大小。在做这类“轻弹簧”问题时,一定要注意弹簧两端受力平衡,合力为零,但加速度并不一定为零。
二、质量不可忽略的弹簧——“重弹簧”问题
虽然大多数情况下弹簧的质量都可以忽略不计,但是有些问题里是需要考虑弹簧质量的,此时的弹簧可以称为“重弹簧”。做这类问题时要注意弹簧两端的受力不一定相等,需要对弹簧作受力分析,并利用牛顿第二定律解决问题。
【例2】如图2所示,一质量为M的均质弹簧平放在光滑水平面上,在弹簧的右端施加一水平恒力F,使弹簧从静止开始向右做匀加速直线运动。试分析弹簧上各部分的受力情况。

图2

【点评】本题作为一道分析题,首先,需要学生选取一部分弹簧为研究对象,其次,这部分弹簧作受力分析,最后根据牛顿第二定律解决问题。但是由于题中并未给出弹簧的总长度,导致很多学生不知如何下手,不知最后应该呈现出怎样的结果,对学生来说是一个难点。做这类“重弹簧”问题时,一定要与“轻弹簧”区分开,注意弹簧两端受力不一定平衡,两端受力之差由弹簧的质量及加速度决定,可以通过牛顿第二定律进行求解。
三、弹簧弹力不能突变类问题(瞬时问题)
弹簧的弹力与形变量成正比,其两端一般与物体相连,而弹簧的形变过程需要一段时间,其长度的变化不能在瞬间完成,因此弹簧的弹力是不能在瞬间发生突变的。与弹簧相比,不可伸长的轻绳、轻杆、接触面等产生微小形变的物体,一般认为它们的弹力可以在瞬间发生突变。
【例3】如图3所示,木块A与木块B用轻弹簧相连,并竖直放在木块C上,三者静置于地面,A、B、C三者的质量之比为1∶2∶3。设所有接触面均光滑,当沿水平方向迅速抽出木块C时,木块A和木块B的加速度大小分别为aA=________,aB=________。
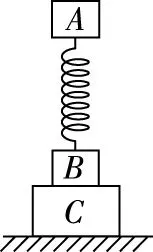
图3
【解析】设A、B、C的质量分别为m、2m、3m。以A为研究对象,抽出C前,A受到重力和弹簧弹力这一对平衡力的作用。在抽出C的瞬间,A受到的重力和弹簧弹力的大小以及方向均不发生变化,故A的瞬时加速度为0。以A、B为研究对象,由平衡条件可知,抽出C前,C对B的作用力为FCB=3mg,方向竖直向上。以B为研究对象,抽出C前,B在重力、弹簧弹力和FCB三个力的作用下平衡,抽出C的瞬间,B受到的重力和弹簧弹力的大小以及方向均不发生变化,而FCB瞬间变为0,故B受到的瞬时合外力大小为3mg,方向竖直向下,瞬时加速度大小为1.5g。
【点评】瞬时加速度问题在力学问题中一直是一个热点,同时也是学生容易出错的地方,解决这类问题时,首先,要按照连接物的形变特点将其分为能在瞬间发生突变的微小形变(包括不可伸长的轻绳、轻杆和刚性面等)和不能瞬间发生突变的明显形变(包括弹簧、橡皮筋和弹性面等),然后再根据各自的特点结合牛顿第二定律来解决相关问题。本题中将C抽出的瞬间,可以认为弹簧的弹力不会发生变化,依旧等于A的重力mg,所以抽出C的瞬间A依旧处于平衡状态,加速度为零,而抽出C时B不再受C的支持力,故B此时受到的合力方向向下,然后根据牛顿第二定律即可算出B的加速度。
四、弹簧形变量与物体位移相关联的问题
弹簧的弹力大小满足胡克定律F=kx,其中x为弹簧的形变量。当弹簧两端与物体相连时,x可以与物体位移相关联,因此弹簧模型可以与动力学的相关知识结合起来进行考查。做此类问题时要注意弹簧的形变是压缩还是伸长,物体位移的方向,位移与形变量的大小关系等。
【例4】如图4所示,在倾角为θ的光滑斜面上有两个用轻弹簧相连接的物块A、B,其质量分别为mA、mB,轻弹簧的劲度系数为k,C为一固定在斜面上的挡板,整个系统处于静止状态。现用一恒力F(F已知)沿斜面向上拉物块A使其沿斜面向上运动,求物块B刚要离开挡板C时物块A加速度a的大小和从开始到此时A的位移大小d(重力加速度为g)。

图4
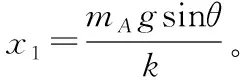
【点评】在做与弹簧相关的动力学问题时,要注意弹簧弹力随形变量发生线性变化的特点,将弹簧的形变量与物体的位移联系起来,找出二者之间的联系,然后再根据形变量计算弹簧弹力,进而根据牛顿第二定律解题。本题中随着物块A沿斜面向上运动,弹簧从压缩状态逐渐变为伸长状态,弹簧形变量的改变量即为物块A的位移大小,然后根据初末状态下物体的受力状态解出弹簧的形变量大小,从而计算出整个过程中物块A的位移,然后再对物块A受力分析,通过牛顿第二定律,便可计算出末状态下物块A的加速度大小。
五、弹簧模型与能量相结合问题
弹簧在伸长或压缩时都会储存一定的弹性势能,因此弹簧的弹性势能可与机械能守恒定律相结合进行考查,要注意弹簧在形变量大小相等时所具有的弹性势能相等,无论其处于伸长或压缩的状态。
由功能关系可知,弹簧弹力做功等于弹性势能的变化量,但弹簧弹力做功是变力做功,一般可以用以下方法求解:

(2)利用F-x图象与横轴所围成的面积大小求解;
(4)根据动能定理或能量守恒定律求解。
由于弹性势能与弹性形变有关,而弹性势能的计算公式在高考中不作定量要求,因此在求弹簧弹力做功或弹性势能改变量时,一般要从能量转化与守恒的角度来分析。特别是在运动过程的初末状态弹簧形变相等的情况下(一般情况下,初末状态分别处于伸长或压缩状态,且形变量大小相等),往往弹性势能的改变量可以抵消或替代求解。
【例5】如图5所示,质量为m的物块A用一轻弹簧与下方地面上质量也为m的物块B相连,开始时A、B均处于静止状态,此时弹簧的压缩量为x0。用一条不可伸长的轻绳绕过轻滑轮,一端连接物块A,另一端C握在手中,整条绳处于伸直状态且张力为零,A上方的绳子沿竖直方向且足够长。现对C端施加一水平恒力F=3mg,使A从静止开始向上运动,则当B刚要离开地面时A的速度为多大?(整个过程弹簧始终处于弹性限度以内,且忽略所有摩擦)

图5

【例6】如图6所示,质量为m1的物体A经一轻质弹簧与正下方地面上质量为m2(m2>m1)的物体B相连,弹簧的劲度系数为k,初始时物体A、B都处于静止状态。用一不可伸长的轻绳一端绕过轻滑轮连接物体A,另一端连接一轻挂钩。开始时各段绳都处于伸直状态且张力为零,物体A上方的一段绳沿竖直方向悬挂。现给挂钩挂一质量为m2的物体C并使其从静止释放,则释放物体C后恰好能使物体B离开地面但不继续上升。若将物体C换成另一质量为(m1+m2)的物体D,仍从上述初始位置由静止释放,则这次物体B刚离地时物体D的速度大小是多少?已知重力加速度为g。

图6
【解析】开始时物体A、B均静止,设弹簧的压缩量为x1,有kx1=m1g,悬挂物体C并释放后,C向下运动,A向上运动,设B刚要离地时弹簧伸长量为x2,有kx2=m2g,B不再上升表明此时A、C的速度均为零,即C已下降到其运动的最低点,与初状态相比,由机械能守恒定律可得弹簧弹性势能的增加量为ΔE=m2g(x1+x2)-m1g(x1+x2)。将C换成D后,B离地时弹簧弹性势能的增加量与前一次相同,由能量守恒定律可得
【点评】在分析问题时要注意弹力的大小与方向时刻与弹簧瞬间的形变量相对应。解决此类问题时,一般先从弹簧形变的分析入手,先确定弹簧的原长位置、现长位置和临界位置,然后找出形变量x与物体空间位置变化的几何关系,分析形变量所对应的弹力大小和方向。同时也要注意弹簧的弹性势能与形变量的对应关系,以此分析物体运动状态和能量的变化情况。在例5中,弹簧在初末状态下虽然处于不同的形变状况,但形变量的大小相等,因此对应的弹性势能也相等,整个过程中弹簧弹力做的总功为零,运用动能定理或能量守恒关系时就不用再考虑弹力做功和弹性势能的改变了。在例6中,弹簧在初末状态的形变量虽然不同,但可以根据第一个过程中的能量守恒关系计算出整个过程中弹性势能的变化量,然后根据第二个过程中的能量守恒关系解出物体D的末速度大小。
六、与弹簧相关的临界极值问题
通过弹簧相连的物体,在运动过程中常常会涉及临界极值问题,例如物体速度达到最大、两个物体速度相同时弹簧形变量达到最大、物体恰好要离开地面及相互接触的物体恰好要脱离等情形。解决此类问题的关键在于利用临界条件结合动力学规律和功能关系、能量守恒关系得到与解题相关的物理量和结论。
【例7】如图7所示,A、B两个木块叠放在竖直轻弹簧上,已知A、B的质量分别为0.42 kg和0.40 kg,弹簧的劲度系数为k=100 N/m。现在A上施加一个竖直向上的变力F,使A由静止开始以0.5 m/s2的加速度竖直向上做匀加速运动。重力加速度为g=10 m/s2

图7
(1)在A竖直向上做匀加速运动的过程中,求力F的最大值;
(2)若A由静止开始做匀加速运动,直到A、B分离的过程中,弹簧的弹性势能减少了0.248 J,求这一过程中F对木块做的功。
【解析】此题的难点在于能否确定A、B两木块分离的临界点。当F=0(即不加竖直向上的力)时,设木块A、B叠放在弹簧上处于静止时弹簧的压缩量为x,则

现对木块A施加力F,则A、B的受力如图8所示,对木块A有

图8
F+FN-mAg=mAa②
对木块B有
kx′-FN-mBg=mBa③
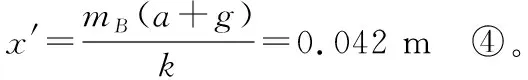
【点评】临界极值问题一直以来都是高中物理中的一大热点问题,无论是力学还是电磁学都会涉及,在这些问题中与弹簧相关的问题占了很大的比例。在解决与弹簧相关的临界问题时,最重要的是分析临界状态的特点以及达到临界状态所要满足的物理条件。本题中最重要的是要确定A、B两木块分离的临界点,即二者间的相互作用力FN=0且二者加速度相等的状态,然后在临界状态下分别对两物体做受力分析,根据牛顿第二定律和功能关系解出两物体在临界状态下的相关物理量,从而解出整个过程中力F的最大值和力F对木块做的功。

