电磁感应问题中导体滑动距离求解的三种思路

湖北 许 文

在闭合回路中一部分导体做切割磁感线运动类的电磁感应问题中，导体受到安培力大小与导体运动的速度大小有关。若无其他外力的作用，导体做非匀变速运动。在这种问题中求导体运动的距离，需要有较强的知识整合能力与思维能力。本文通过典型实例分析，从知识与思维两个维度，归纳总结此类问题求解的三种思路。

一、问题与思路

【问题】如图1所示，MN、PQ是位于同一水平面上、相互平行、足够长的光滑金属导轨，两导轨相距L，电阻不计，其左端用导线连接一个阻值为R的定值电阻，将一个质量为m，电阻为r的导体棒垂直于导轨放置，整个装置处在垂直于导轨平面、范围足够大的磁感应强度为B的匀强磁场中。现给导体棒一个沿轨道方向的水平初速度v0，导体棒沿导轨运动过程中始终保持与导轨垂直，且接触良好。求导体棒在整个过程中的位移大小x。

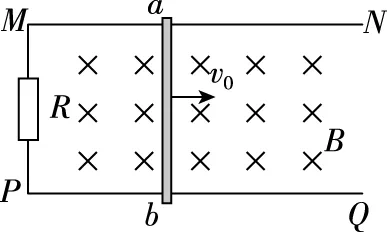
图1

【思路】

思路1(用微元法求解)导体棒在整个过程中做加速度减小的减速运动，若将其运动过程分成很多微小段，可认为导体棒在每个微小段内做匀变速运动。

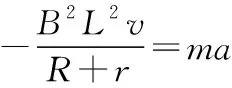
小结1 利用微元法求解，将导体棒的整个运动过程分成很多微小时间单元，在每个微元内，可认为导体棒是匀变速运动或匀速运动，利用匀变速运动与匀速运动的相关规律求出这个微元内导体棒运动的位移，然后再求其和。微元法是处理变化问题的基本方法之一，其核心的思想是化变为恒，通过先微分后积分的方式解决问题，这种方法对物理建模能力及数学知识的运用能力要求较高。

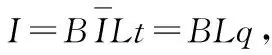
整个过程对导体棒分析，由动量定理得

小结2 动量定理求解，巧妙地利用了安培力的平均冲量与感应电荷量间的关系、感应电荷量与回路中磁通量的变化关系。回路中磁通量的变化量与导体棒运动的位移大小有关，与运动时间无关。这种方法对知识的整合度要求较高。

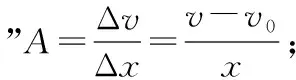
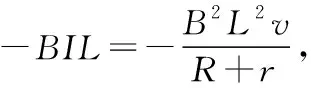
小结3 利用“另类匀变速运动”规律求解，要根据“相等位移内速度的变化相等”这一特征，结合牛顿运动定律与匀变速运动规律，导出“另类匀变速运动”的受力及运动规律的表达式。这种方法对知识的理解与迁移能力要求较高。

二、应用与练习

【例题】如图2所示，空间等间距分布着水平方向的条形匀强磁场，竖直方向磁场区域足够长，磁感应强度B=1 T，每一条形磁场区域的宽度及相邻条形磁场区域的间距均为d=0.5 m。现有一边长l=0.2 m、质量m=0.1 kg、电阻R=0.1 Ω的正方形线框MNOP以v0=7 m/s的初速度从左侧磁场边缘水平进入磁场，求：

图2

(1)线框MN边刚进入磁场时受到的安培力大小F；

(2)线框从开始进入磁场到竖直下落过程中产生的焦耳热Q；

(3)线框能穿过完整条形磁场区域的个数n。

【解析】(1)线框MN边刚进入磁场时产生的感应电动势大小为E0=Blv0

解得Q=2.45 J

(3)选取水平向右为正方向。当线框水平方向速度减为零时，线框在有安培力作用过程中沿水平方向运动的总距离为x。

解法1 设线框在进入和穿出条形磁场过程中水平速度为v时，其水平方向的加速度为a，由牛顿第二定律有

在一段很短的时间Δt内线框的水平速度变化Δv，有

在时间Δt内线框水平方向的位移为

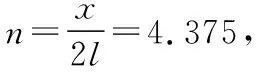
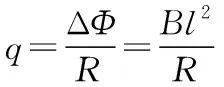
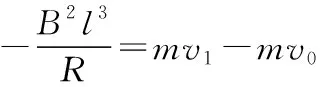
同理线框穿过第1个条形磁场右边界过程中有

故线框穿过第1个条形磁场全过程中有

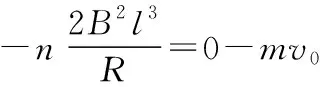
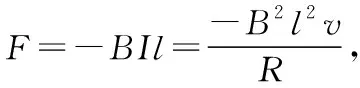
图3