“水平面上板块类情景问题”浅析
2020-11-13山西田郭政
山西 田郭政
板块类情景是高考中常见的情景和模型。学生对此类问题经过高考复习形成了条件反射,一见到“板块类情景问题”总认为动量守恒。即使不按动量守恒分析,也对物体的运动情景非常糊涂,因此为了找准板块类问题分析的切入点和分析方法;进一步巩固和强化“动力学观点”“能量观点”“动量观点”三大方法解决此类问题的能力;切实提高学生的审题能力、情景类问题分析处理能力,养成具体问题具体分析的良好习惯;切实把“课堂阵地追求高效”发挥到最高水平,特就此类问题经过母题的不断变化,达到“一题多变→发散思维”“一题多思→严密思维”“一题多解→活跃思维”“多题归一→整合思维”之目的,不断提高学生物理学科的核心素养。
【母题】如图所示,质量M=4.0 kg的木板长L=0.75 m,静止在光滑水平面上,在其左端静止另一质量m=1.0 kg的小滑块,它们之间的动摩擦因数μ=0.2。现对滑块施加一向右的水平恒力F,要使滑块在1.0 s末恰从木板右端滑出,力F应为多大?(g取10 m/s2)
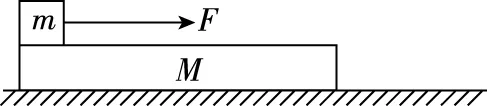
图1
【解析】这是一道常规题,从题目的类型来说应属于动力学两类问题中“已知运动求受力”这类问题。其实质就是水平面上的相对运动问题,只不过有约束条件:一是木板定长;二是拉出有时间限制。所以只需要对木板、小滑块分别进行受力分析,利用木板定长这个约束条件就可顺利解决问题。
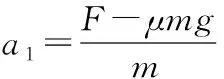
其中滑块的位移比木板的位移多L,即x1=x2+L
联立以上各式,代入数据,解得F=4 N
以下变式中木板均置于光滑水平面上;木板、滑块的质量不变,木板与滑块间的动摩擦因数不变。
【变式一】如图2所示,质量M=4.0 kg的木板长L=1.3 m,在其右端有另一质量m=1.0 kg的小滑块,它们之间的动摩擦因数μ=0.2,木板置于光滑的水平面上。开始时木板和滑块均静止,现对木板施加一向右的水平恒力F=26 N,要使滑块从木板上掉下来,力F至少作用多长时间?(g取10 m/s2)

图2
【变式目的】与母题相比,力F作用的对象、设问、滑块的初位置都变了,并且力F仅作用一段时间。学生如果先做了前面的题目,会感觉简单。经此变式后学生能做到具体问题具体分析,顺利解出为本题变式的目的。
【解析】力F作用下,滑块和木板一定发生了相对运动;F作用了时间t1撤销后,滑块继续加速运动,木板减速。经时间t2滑块能从木板上恰好滑下时,力F作用的时间最短。滑块恰好滑下时,滑块和木板的速度应相同,设为v3,这一条件是学生分析时不容易找到的。
在t1时间内,滑块的加速度
a1=μg=2 m/s2,v1=a1t1
在t2时间内,滑块的加速度
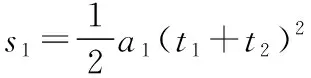
而s2-s1=L
解得t1=0.5 s
【点评】本题的难点之一在设问中就隐含着木板的运动过程不单一;其次,求物理量的范围问题,就是求临界值问题;再者,找滑块恰好从木板上刚好滑离的临界条件也是一困难点。学生只有具备了良好的解题习惯,重视物理过程的分析,抓住问题的实质,挖掘出隐含条件,分清运动过程的联系,才能提高运用知识解决实际问题的能力。
【变式二】如图3所示,质量M=4.0 kg的小车置于光滑的水平面上,在小车右端施加一水平恒力F=8 N。当小车向右运动速度达到v=1.0 m/s时,其右端轻放质量m=1.0 kg的小物块,它与小车之间的动摩擦因数μ=0.2,在小车的右端轻放此物块,假定小车足够长,求小物块从放在车上开始经过t=3.0 s相对地面所通过的位移是多少?(g取10 m/s2)
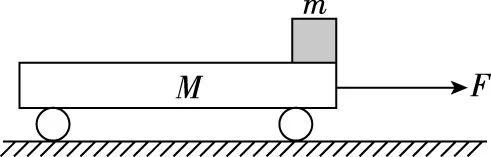
图3
【变式目的】本题求小滑块相对地面的位移。但是小滑块不在地面上运动而是在运动的小车上,不能误认为小滑块在地面上运动进行简单处理。其次,本题变式后对小滑块在3.0 s内的运动情况不能单一是分析的另一个关键;小滑块在3.0 s时间内后一阶段的运动中是否能和小车一起保持相对静止共同做匀加速直线运动是需要看小滑块是否满足它的最大静摩擦力不小于ma(a为它们共同运动的加速度),如没有考虑到这一点,将很容易导致错误。
【解析】物块放上小车后做初速度为零、加速度为a1的匀加速直线运动,小车做加速度为a2匀加速直线运动。
物块的加速度为a1=μg=2.0 m/s2
设经过时间t,物块在小车上停止相对运动时,它们具有共同的速度,根据题意可知
v1=a1t,v2=v+a2t
由v1=v2得t=2 s
物块在前2 s内做加速度为a1的匀加速直线运动,后1 s 同小车一起做加速度为a的匀加速直线运动。以系统为研究对象,根据牛顿第二定律由F=(M+m)a得
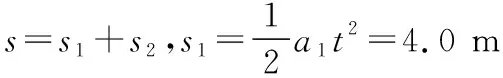
s=s1+s2=8.8 m
【点评】由于学生对题目所给条件不加斟酌,比如小车足够长,会出现好多错误,一类同学误认为系统动量守恒,求出物块滑离小车时的速度。而大部分同学对运动过程分析不清,因为在3.0 s内小车和物块的运动不单一,学生容易按物块仍以2.0 m/s2匀加速直线运动求3.0 s内的位移。
【变式三】如图4所示,质量m=4.0 kg的木板B的右端固定一根轻弹簧,弹簧的自由端C到木板左端的距离L=0.5 m,而弹簧的自由端C到弹簧的固定端D之间的木板是光滑的。木板始终在光滑的水平面上运动。滑块A原来静止在木板的左端,滑块A与木板B上弹簧的C端之前的动摩擦因数μ=0.2。若木板受到一水平向左的恒力F=14 N,且作用一段时间后撤去该力,这时滑块A恰好到达弹簧的自由端C处。假设A、B间的最大静摩擦力等于滑动摩擦力。(g取10 m/s2)求滑块A在滑动过程中弹簧的最大弹性势能。

图4
【变式目的】本题巧妙设置滑块与弹簧接触前为一个简单的相遇问题,并没有直接给出滑块与弹簧接触时它们的速度,仍然想借它们发生相对运动知识来获得各自的速度。再者力F作用结束后,学生可能又会受思维定式的影响,又去对它们进行隔离,分析它们的运动情况,导致分析得很复杂,最后也找不到弹簧弹性势能最大时的条件。
【解析】本题很明显一开始滑块和木板发生了相对运动,以不同的加速度做各自反向的匀加速直线运动。对滑块maA=μmg,aA=μg=2 m/s2
对木板MaB=F-μmg解得aB=3 m/s2
根据题意有sB-sA=L
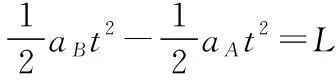
代入数据,解得水平恒力F作用的时间t=1.0 s
弹簧的弹性势能最大时,说明系统的动能损失最大。所以对系统从能量守恒的角度去分析弹簧弹性势能最大的条件就容易些。
1 s末滑块和木板的速度分别为
vA=aAt=2 m/s,vB=aBt=3 m/s
撤去F后,当滑块A和木板B的速度相等时,弹簧的弹性势能最大。
根据动量守恒定律mvA+MvB=(M+m)v
代入数据解得v=2.8 m/s
由机械能守恒定律得
代入数据,解得E弹=0.4 J
【点评】这种情境有意识地避开学生直接根据思维定式套用结果,因为许多学生清楚它们的速度相等时,系统的动能损失最大。所以一开始设置了一个相遇问题,通过滑块和木板的相对运动情境来获得滑块与弹簧接触时速度。这样做一方面充分体现了物理量给出方式的情景化;另一方面,把碰撞中的完全非弹性碰撞条件的实质体现在具体的问题中,从而不断提高学生运用知识解决实际问题的能力。
【变式四】如图5所示,质量mA=4.0 kg的木板A和质量mB=1.0 kg的小物块B处于静止状态,小物块B视为质点。木板A与水平面间的动摩擦因数μ为0.2。现突然给木板一个水平向右的12 N·s的瞬时冲量I作用后,木板开始运动,当小物块滑离木板时,木板的动能EkA为8.0 J,小物块的动能EkB为0.50 J,重力加速度取10 m/s2,求木板的长度L(g取10 m/s2)。

图5
【变式目的】改变已知中的一些说法,比如,已知冲量、动能,关键看学生概念是否清楚,因为物理规律必须有概念的支撑,这是我们学好物理必须具有的学科素养。
【解析】设水平向右为正方向,由I=mAv0解得
v0=3.0 m/s
设小物块滑离木板时A、B的速度大小分别为vA、vB,则由EkA=8.0 J,EkB=0.50 J解得
vA=2 m/s,vB=1 m/s
这段过程对A、B系统由动量定理得
-ft=(mAvA+mBvB)-mAv0
其中f为A与地面的摩擦力f=μ(mA+mB)g
解得t=0.3 s
这段过程对A、B发生的位移分别为
所以木板的长度L=sA-sB=0.60 m
【点评】本题从知识结构上来看,在已知量的给出中加强对概念的考查,在解析中重点考查对规律、方法的灵活运用,比如用平均速度求位移以及用动量定理求解物理量是我们不常使用的公式,在此强化这方面的理解和运用。

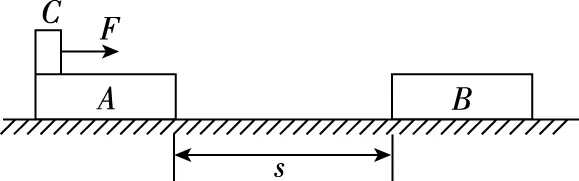
图6
【变式目的】把物块和木板一开始总会发生相对运动,转变为不发生相对运动,使碰撞的物理情景更加明朗化,但学生若不推敲,认为碰撞时三个物体组成的系统还受外力F,所以碰撞时系统动量不守恒。出现这种情况就是由于对碰撞的特点分析不够,实际上系统动量守恒有多种情况,可分为绝对守恒、近似守恒、单方向守恒等,本题中碰撞属于动量近似守恒问题。
【解析】本题涉及的研究对象多,物理过程复杂,若对物理过程分析不清的话,就很难解出来。
设A、C之间的滑动摩擦力大小为f1,A与水平地面之间的滑动摩擦力大小为f2,由μ1=0.22,μ2=0.10可知
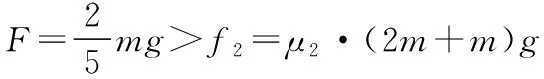
所以一开始A和C保持相对静止,在F作用下向右一起做匀加速运动,即
A、B两板的碰撞瞬间,根据动量守恒定律可知
mv1=(m+m)v2
碰撞结束后到三个物体达到共速的过程中,设木板向前移动的位移为s1,选三个物体构成的系统为研究对象,合外力之和为零,则
2mv1+(m+m)v2=(2m+m+m)v3
设A、B系统与水平地面之间的滑动摩擦力大小为f3,对A、B系统由动能定理得
其中f3=μ2(2m+m+m)g
对物块C,由动能定理得
由以上各式代入数据计算得l=0.3 m
【点评】本题难度大的原因有以下几点:一是研究对象增加;二是物理过程变得更复杂;三是处理问题的物理方法增多,使用的物理规律也增多。不仅如此,运动中的临界条件增多且不容易找到;四是数学运算能力的要求升高。由此可见,只有养成严谨的思维,对物理学科的核心知识和规律理解透彻,同时善于分析模型问题的实质才会使问题得到解决。
总 述
“水平面上板块类情景问题”所涉及的模型大家都知道,也是高考常见的题型。本文遵循由易到难的顺序展开问题的分析,是为了增强学生学好物理的信心和获得感;改变模型的设问,是为了强化学生运用知识的灵活性;改变前提条件,是为了扩大学生分析问题的视角;通过对这些题目的分析,可以说把力学中经常让我们求解的物理量都涉及了,同时,在每道题目中都有学生易错易混的知识盲区,这样做有助于提高学生对物理概念、规律的进一步认识,从而真正做到提高学生核心素养之目的。
通过对“水平面上板块类情景问题”的分析,我们会发现,凭经验和感觉做题是不可取的,必须切合题目的条件和设问认真分析问题的本质,才可能解出来,所以在平时加强对解题基本功的训练很有必要。一般解答这种模型时,第一关是审题,并且审题应贯穿在整个解题过程中,这是做题的关键和前提。第二关是确定研究对象,分析物理过程。应将大过程分解成若干子过程,在分析物理过程中要找到子过程间的联系,同时不可忽视隐含条件的挖掘和干扰因素的排除。第三关是选择对应的规律(公式),在运用规律和公式时一定要注意是否有适用条件,切忌不加思考乱套公式。通过前面的例题,我们可以看到,在中学物理中常常用到的“动力学观点”“能量观点”以及“动量观点”都有涉及,这样做对学生综合分析能力一定有提高。
另外,关于“板块类情景问题”可能老师们还会想到斜面上的板块类问题,甚至把滑块换成盘子,把木板换成桌布等在形式上的一些改变,其实,换汤不换药,只要我们紧紧抓住解题的根本就能在高考中取得好成绩。

