运用库仑定律解题时的易错分析
2020-11-13安徽陶士金
安徽 方 林 陶士金
库仑定律是电磁学的基本定律,也是中学物理的重要规律。对定律理解不透彻,在解题时就会出现种种错误。而将这些易错资源加以整合剖析对落实科学思维素养无疑有很大益处。本文将运用库仑定律解题存在的一些典型错误进行梳理,供大家参考。
一、不清楚库仑定律的适用条件
【例1】如图1所示,有两个完全相同的半径为a的带电金属球分别处于真空中的两个绝缘支架上,球心相距为3a,所带电荷量分别为Q1、Q2,静电力常量为k,则二者之间的库仑力大小
( )

图1


【小结】库仑定律计算的是真空中的两个点电荷之间作用力。点电荷是一个理想化的模型,实际问题中,只有当带电体间的距离远大于它们自身的线度,以至于带电体的形状和大小对相互作用力的影响可以忽略不计时,带电体方可视为点电荷。
二、未注意电荷量的改变
【例2】一根放在水平面内的绝缘光滑玻璃管,内部有两个完全相同的弹性金属小球A和B,所带电荷量分别为+9Q和-Q。两小球从图2中所示位置由静止释放,那么,两小球再次经过图示位置时,A球的瞬时加速度与释放时的比值为
( )

图2

C.1
【易错分析】本题易错选项为C项。因为没有考虑到两小球带异种电荷,相碰时要发生电荷量中和现象,分开后各自的电荷量已经改变。

【小结】库仑定律可以计算电荷间的相互作用力,而无论电荷的正负,运用定律计算时,一定要注意要代入电荷量的绝对值,方向另外判断。
三、未注意电荷间距的变化
【例3】如图3所示,真空中A、B两个点电荷的电荷量分别为+Q和+q,放在光滑绝缘水平面上,A、B之间用绝缘的轻弹簧连接。当系统平衡时,弹簧的伸长量为x0。若弹簧发生的均是弹性形变,则
( )

图3
A.保持Q不变,将q变为2q,平衡时弹簧的伸长量等于2x0
B.保持q不变,将Q变为2Q,平衡时弹簧的伸长量小于2x0
C.保持Q不变,将q变为-q,平衡时弹簧的缩短量等于x0
D.保持q不变,将Q变为-Q,平衡时弹簧的缩短量小于x0
【易错分析】本题易出现错误之处在于库仑定律中两电荷之间距离的判断,很多同学只注意到电荷量的改变,而未注意到电荷间距的改变。由于电荷量的变化是一个动态变化的过程,因此随着库仑力的改变,应将新的平衡状态与原有状态作比较。

【小结】在用库仑定律判断或计算该类问题时要注意:1.电荷间是吸引力还是排斥力;2.在电荷间距离不变的情况下库仑力才与电荷量的乘积成正比,往往题中电荷量变化时距离也随之变化;3.库仑定律中的距离与弹簧形变量不同。
四、不会整体分析受力
【例4】如图4所示,质量均为m的三个带电小球A、B、C放置在光滑绝缘的水平直槽上,A、B间和B、C间的距离均为L。已知A球带电荷量为QA=+8q,B球带电荷量为QB=+q,若在C球上施加一个水平向右的恒力F,恰好能使A、B、C三个小球保持相对静止,共同向右加速运动。求:
(1)拉力F的大小;
(2)C球所带电荷量QC。

图4
【易错分析】本题易错误之处在于受力分析时容易丢力,如很多同学在分析C的受力时会丢掉A施加给它的吸引力。
【正确解析】因为A、B、C三小球保持相对静止,故有相同的加速度
对它们所组成的整体,由牛顿第二定律有F=3ma
对A分析:C的电性应与A和B异性,有


【小结】本题若能正确对C进行受力分析,然后列出牛顿第二定律也能求解,但不少同学会因为C受力较多而出错,尤其初学者会丢掉A对C的吸引力。而如果对A、B、C整体列牛顿第二定律,既可以避免分析受力出错,也可以使方程简化,便于求解。当系统内各物体具有相同的加速度时,应先把这个系统当作一个整体(即看成一个质点),分析受到的外力及运动情况,利用牛顿第二定律求出加速度,如果要求系统内各物体相互作用的内力,则需将物体隔离,对某个物体单独进行受力分析,再利用牛顿第二定律对该物体列式求解。
五、未注意到多解性
【例5】如图5所示,三个固定的带电小球a、b和c,相互间的距离分别为ab=5 cm,bc=3 cm,ca=4 cm。小球c所受库仑力的合力的方向平行于a、b的连线。设小球a、b所带电荷量的比值的绝对值为k,则
( )

图5
A.c点场强方向一定平行于ab向左
B.c点场强方向一定平行于ab向右


【易错分析】本题易错之处在于因电场方向有两种可能而造成多选。
【正确解析】由题意可得,小球c所受库仑力的合力的方向平行于a、b的连线,对小球c所受的库仑力分析,若a、b的电荷同号,则电荷c所受的库仑力的合力不可能平行于a、b的连线,只有当a、b的电荷异号,小球c所受的库仑力如图6所示或是其反方向(图中未标出),AB选项错误;电荷c所受库仑力的合力才可能平行于a、b的连线,则Fa ccos53°=Fb ccos37°
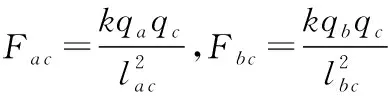

故选项D正确。

图6
【小结】在定性分析电场问题时,往往会因为电性不确定而造成多解。分析时,一定要注意有没有多种可能。
六、未能建立正确情景

图7
【例6】水平面上A、B、C三点固定着三个电荷量为Q的正点电荷,将另一质量为m的带正电的小球(可视为点电荷)放置在O点,OABC恰构成一棱长为L的正四面体,如图7所示。已知静电力常量为k,重力加速度为g,为使小球能静止在O点,小球所带的电荷量为
( )
【易错分析】本题易错之处在于对小球受力分析时不会考虑对称性的特点,此外由于空间想象能力不够,不会求各力间的夹角,导致不会列平衡方程。

【小结】若物体在三维立体空间中多力作用下而平衡,可以通过合成或分解法将力降至二维平面内,然后再选择合适方法分析处理,在分析问题时还应注意利用对称性简化问题。
综上所述,在运用库仑定律解答问题时,既要注意定律的适用条件,也要注意有无因电性不确定而引起的多解,还要能根据物理情境正确建模,选择合适的思路求解问题,以避免出现种种错误。

