刍谈热力学实体问题的模型建构

福建 郑行军

实体问题是以生活中的物、事、现象等为载体，设计条件、设问等试题主体结构，通过日常的逻辑感知、推理编写题干概要，模拟出与实际情境相契合的新型试题。实体问题的建构和试题编制体现了物理学理论联系实际，注意与科学技术、社会和经济发展的联系，注意知识在日常生活、生产劳动实践等方面的广泛应用等学科特征，符合新课改“一核四层四翼”的考试评价体系要求，因此在近年的高考试题中呈现较高频的命题趋势。

相较于物理学科其他分支的实体模型设计，热力学的实体问题具有以下个性特征：

1.实体模型与理想化模型存在较大的偏差，需对实际情境进行理想化处理，转化为熟悉或可见的常规物理模型，运用类比、演算、分化或组合等方法剖析求解。

2.实际的物理问题会比较抽象、复杂，需要从不同的角度或用不同的方法处理，相关知识之间要求学生具有灵活应用所学知识处理问题的能力，具备较高的学科素养。

3.热力学状态参量的分析与功能关系的研究融合数学方法，要根据数理学科间的紧密关系和思维互通性，形成数理知识、思维交汇融合的多元化解题思路。

因此探究热力学实体问题的模型建构和分析思维，对于提升学生的物理建模能力、学科融合能力、推理分析能力等方面都具有积极的意义。

一、定量型实体问题

以实际生活中的封闭型对象为载体，题干设定空间内(理想)气体的质量始终不变构建定量型实体模型，在外界因素(如力、温度、能等)发生变化时，会导致实体内气体的状态发生变化，其本质仍然是气体实验定律和热力学第一定律的综合应用。模型的建构聚焦于宏观和微观两个角度：宏观模型以气体实验定律为基础，探究实体变化过程压强、体积和温度变化的特征，综合动力学方程、功能关系、热力学定律、能量守恒定律等通过推理和演算，得到系统中各种宏观状态量之间的关系及宏观过程方向、限度的规律；微观模型则以大量微观粒子无规则运动的统计规律出发，结合分子动理论、气体热现象、固体和液体的微观解释等微观结构知识，对粒子相互作用的性质和规律及热现象本质，应用统计的方法，找出宏观量与微观量的关系，最终获得系统的宏观性质和宏观量遵从的规律。

【例1】受啤酒在较高压强下能够溶解大量二氧化碳的启发，科学家设想了降低温室效应的“中国办法”：用压缩机将二氧化碳送入深海底，由于海底压强很大，海水能够溶解大量的二氧化碳使其永久储存起来，这样就为温室气体找到了一个永远的“家”。现将过程简化如图1所示：在海平面上，开口向上、导热良好的气缸内封存有一定量的CO2气体，用压缩机对活塞施加竖直向下的压力F，此时缸内气体体积为V0、温度为T0。保持F不变，将该容器缓慢送入温度为T、距海平面深为h的海底。已知大气压强为p0，活塞横截面为S，海水的密度为ρ，重力加速度为g。不计活塞质量，缸内的CO2始终可视为理想气体，求：

图1

(1)在海底时CO2的体积；

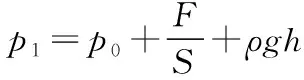
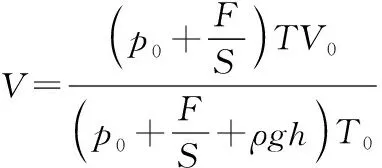
解得F′=2F+(p0+ρgh)S

【点评】本题以容纳CO2气体的气缸为载体建构了一个封闭型空间，以内部气体为研究对象考查气体实验定律，动力学关系等，因此解题的聚焦重点仍集中在状态量的判断和计算。由平衡方程，求出气体在海平面和海底的压强，根据理想气体状态方程解出在海底时CO2的体积；本题解题关键在于明确题设研究对象为定量型实体，剖析缸中气体变化的特点，知道气体发生什么变化，求出气体的状态参量，然后选择适当的气体状态方程列式求解。

二、充气型实体问题

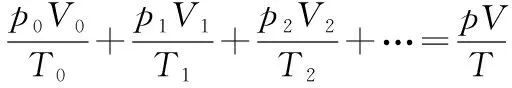
【例2】热等静压设备广泛用于材料加工中。该设备工作时，先在室温下把惰性气体用压缩机压入到一个预抽真空的炉腔中，然后炉腔升温，利用高温高气压环境对放入炉腔中的材料加工处理，改善其性能。一台热等静压设备的炉腔中某次放入固体材料后剩余的容积为0.13 m3，炉腔抽真空后，在室温下用压缩机将10瓶氩气压入到炉腔中。已知每瓶氩气的容积为3.2×10-2m3，使用前瓶中气体压强为1.5×107Pa，使用后瓶中剩余气体压强为2.0×106Pa；室温温度为27℃。氩气可视为理想气体。

(1)求压入氩气后炉腔中气体在室温下的压强；

(2)将压入氩气后的炉腔加热到1 227℃，求此时炉腔中气体的压强。

【解析】(1)设初始时每瓶气体的体积为V0，压强为p0；使用后气瓶中剩余气体的压强为p1。假设体积为V0，压强为p0的气体压强变为p1时，其体积膨胀为V1，由玻意耳定律得p0V0=p1V1

被压入进炉腔的气体在室温和p1条件下的体积为

V′=V1-V0

设10瓶气体压入完成后炉腔中气体的压强为p2，体积为V2，由玻意耳定律得p2V2=10p1V′

联立方程并代入数据得p2=3.2×107Pa

联立方程并代入数据得p3=1.6×108Pa

【点评】本题以热等静压设备和压缩机为载体考查了充气问题，解析中采用了转换对象法，以瓶中气体为研究对象，使用前后瓶中气体发生等温变化，根据玻意耳定律即可求出使用后的总体积；再对10瓶中压入炉腔内的气体分析，求出气体初末状态的状态参量，然后应用玻意耳定律可求出炉腔中气体的压强；炉内气体体积不变，气体发生等容变化，根据题意求出气体状态参量，应用查理定律可以求出炉腔内气体的压强。

方法二—守恒法：以热等静压设备和压缩机为整体研究对象，充气前后根据理想气体状态方程10p0V0=10p1V0+p2V2，解得p2=3.2×107Pa。

本题解题的关键在于了解题目的本质是充气型实体问题，而后综合气体状态方程，根据题意分析气体状态变化过程，确定题型和求出气体状态参量是解题的前提与关键。

三、放气型实体问题

放气型实体问题是以实物情境为载体，实体内部气体与外界环境发生物质交换，使实体内气体的质量逐渐减少，放气型实体的本质仍是变质量气体问题。因此命题的角度与充气型实体具有极高的相似性，主要也是集中在：①气体状态量的变化研究；②气体压强的动力学特征分析；③放气过程气体的能量变化；④放气临界问题的研究等几个问题上，但又有所区别：①放气过程可近似看成等温过程；②放气过程每次气体的初压强为上一次放气完毕的终压强，初压强是不断变化的。处理方法有：转换对象法，将放出的气体和实体中剩余的气体作为整体研究，使变质量问题转化为气体总质量不变的状态变化问题。由于每次放气后实体中剩余气体的压强均不相同，应分过程对每次放气过程的始末状态逐次分析；守恒法，利用放气前后气体总物质的量不变，根据理想气体状态方程pV=nRT的分态式p0V0=p1V1+p2V2+…研究。

【例3】如图2所示为某型号的太阳能空气集热器的简易图，底面及侧面为隔热材料，顶面为透明玻璃板，集热器容积为V0，开始时内部封闭气体的压强为p0。经过太阳暴晒，气体温度由T0=300 K升至T1=400 K，为减小集热器内部压强，集热器自动控制系统缓慢抽出部分气体，并使温度降为360 K，此时，集热器内气体的压强回到p0。求：

图2

(1)T1=400 K时气体的压强；

(2)温度降为360 K时，集热器内剩余气体的质量与原来总质量的比值。

(2)以抽出的气体和集热器内的气体为研究对象，设抽出的气体温度也为T2、压强也为p0，此时与集热器内气体的总体积为V。

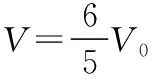
【点评】本题以太阳能空气集热器为载体设计了定量型实体和放气型实体两个模型，太阳暴晒过程气体质量始终不变为定量型实体问题，气体温度升高发生等容变化，根据查理定律求解压强；抽气过程为放气型实体问题，应用转换对象法或守恒法根据气体状态方程求出降温后气体的体积，求解剩余气体的质量与原来总质量的比值等于集热器的容积和降温后气体体积比。分析关键是要注意两个过程模型的区别及气体状态方程适用的条件。

四、分装型实体问题

分装型实体问题即某一封闭型实体的气体分装到几个相同或不同容积的实体中，讨论状态量、力学量和功能量变化的问题。分装型实体模型的特征：①对于气体的分装，可将原有的封闭型实体和分装后的其他实体看作一个整体来研究；②分装后，实体中剩余气体的压强应大于或等于分装后的实体中气体的压强，不存在压强为0的情况。处理思路可以用理想气体状态方程研究。

【例4】医院急诊科为方便急救病人，会把氧气瓶里的氧气分装到几个氧气袋中。已知氧气瓶的容积为20 L，内部压强为3.0×106Pa，现把氧气分装到容积为5 L的氧气袋中，每个氧气袋中原有氧气压强为1.0×105Pa，分装后氧气压强为3.0×105Pa，分装过程气体温度保持不变，氧气可视为理想气体，且分装过程中无漏气，问：

(1)分装氧气过程中，已知外界对氧气做功2.0×104J，分析该过程氧气吸放热情况及多少；

(2)最多能分装多少袋；

(3)请作出分装过程氧气瓶中压强p与氧气袋数量N的p-N图象。

【解析】(1)因为分装过程中温度不变，则ΔU=0

由热力学第一定律ΔU=W+Q

得Q=-W=-2.0×104J

即气体放出2.0×104J的热量。

(2)设最多能分装N个氧气袋，选取氧气瓶中的氧气和N个氧气袋中的氧气整体为研究对象。

分装前后温度T不变，设分装前氧气瓶中的氧气压强为p1，体积为V1，氧气袋中的氧气压强为p2，体积为V2。分装后氧气瓶中的氧气压强为p3，氧气袋中的氧气压强为p4，设p3=p4，根据理想气体状态方程有p1V1+Np2V2=p3V1+Np4V2，代入数据解得N=54袋。

(3)由理想气体状态方程

p1V1+Np2V2=pV1+Np4V2

代入数据得p=(3.0×106-5.0×104N) Pa

得出p-N图象如图3所示

图3

【点评】理想气体的分子势能不计，而温度是分子平均动能的标志，已知外界对氧气做的功，由热力学第一定律可求得氧气吸放热的情况；本题为分装型实体模型，由于分装前氧气袋中已有部分气体，可以氧气瓶和氧气袋为整体研究对象，根据物质的量守恒和理想气体状态方程求解；由理想气体状态方程可得出瓶中气体压强p与氧气袋数量N的关系，可知图象为倾斜直线，在图中作出以上两点，连线即可得出图线。

总体而言，热力学实体模型建构趋向仍是聚焦气体实验定律、理想气体状态方程、热力学第一定律、能量守恒定律和热力学微观诠释等热学主干知识，模型的确定和研究对象的有效选择是实体问题的解题切入点，状态量间的变化关系和合理的处理方法是解题的重要环节。整体的建构思路与其他分支的实体问题设计思想具有一定的共通性，皆是以所学的知识和技能为基础，再与实际生活情境进行有效融合，情境表象外包知识和思维，考查学生理论联系实际的能力及能否将物理知识运用于生活、生产实际，体现了物理学科源于生活，又服务于生活的核心理念(如图4)。实体模型构建可以让学生发现和探究同一知识点在不同环境下的共性和特性，使得在分析不同表象的题目时，能引导学生自主探寻事物的本质，能有一个清晰的物理模型和解题方向，实现化繁为简的目的。

图4