基于核函数和标记权重的多标记特征选择

郑 海 钱 萌

（1.安庆师范大学计算机与信息学院；2.安徽省高校智能感知与计算重点实验室 安徽安庆 246011）

一、引言

近年来，多标记学习得到了广泛的关注。传统监督学习基本都是处理二分类问题，然而，在现实生活中，样本往往具有多义性，样本不仅由一组特征向量描述，同时还与多个标记类别相关，多标记学习框架[1]应运而生，且应用到了文本分类[2]和图像识别[3,4,5]等多个领域。例如，一幅有关动物的图片中，可能同时有“狗”“骨头”“草坪”等标记。

多标记数据的高维性易造成维度灾难[6,7]，维度灾难可能会导致算法运行时间长，分类精度低等问题。特征提取和特征选择是解决高维度问题的两种有效方式。特征选择[8,9]是根据某些准则在原始特征空间选取一组重要的特征子集，并根据特征子集对未知样本进行标记预测。例如Lee等[10]提出了基于多变量互信息的多标记特征选择算法（PMU），该算法利用信息熵度量特征对标记空间的重要程度。Lin等[11]提出了基于邻域互信息的多标记特征选择(MFNMI)，该算法为避免传统信息熵计算混合数据时造成信息损失，提出了邻域信息熵概念，并以此度量特征对标记空间的重要度。

然而，上述多标记特征选择算法在选择特征子集时，都未考虑标记对样本的区分度。不同标记对样本的区分度是不同的，因此，考虑标记对样本的区分度可能有利于提高多标记学习。例如，林梦雷[12]等提出的基于标记权重的多标记特征选择算法，该算法首先利用样本在整个特征空间的分类间隔对标记进行加权，然后在整个标记集合下，特征对样本的可分性为特征赋予权重，根据该权重衡量特征对标记集合的重要程度。魏葆雅[13]等提出基于标记重要性的多标记特征选择算法，该算法首先用核函数将特征空间映射到一个更高维的特征空间，在这个更高维的特征空间中，特征具有可分性，且利用标记对样本的可分性对标记赋权值；然后，在新映射的特征空间中计算样本的分类间隔，并以此作为特征权重度量特征的重要程度。以上这些算法的实验结果表明在考虑标记重要度时，其分类性能有所提高。

另外，核函数是一种能有效解决解决在高维空间运算时遇到的维数灾难问题的方法，其核心思想是对原始数据通过某种非线性映射嵌入到更高维的特征空间中，在这个新的特征空间中根据某个线性分类器将特征区分开，核函数能够简化运算，有效解决非线性问题和高维数灾难等问题。为此，本文提出了一种基于核函数和标记权重的多标记特征选择算法，首先，针对标记空间中的所有标记，分别统计贴有不同标记的样本数量。若对于某个标记，贴有该标记的样本数量明显高于含有其他标记的样本数量，则表明该标记的权重越大。然后，用RFB核函数[14]将特征空间映射到一个更高维的特征空间，在这个新的特征空间中，计算特征与标记空间之间的互信息，根据计算所得的信息熵值对特征进行排序。最后，在多个多标记数据集上进行验证，实验结果表明该算法是有效的。

二、相关知识

定义1[15]随机变量X={x1,x2,...,xq}，随机变量X的不确定期望为，随机变量X的信息熵为

H(X)是随机变量的信息熵，信息熵是度量随机变量不确定性的程度，随机变量不确定性程度越大则信息熵值就会越大。

定义2[15]随机变量X={x1,x2,...,xq}，Y={y1,y2,...yn}，变量X和Y之间的互信息定义为：

I(X;Y)是用于衡量变量X和Y之间的相关性，若I(X;Y)=0，则表示变量X和Y相互独立，I(X;Y)数值越大则表示两者之间的相关性越强。另外，I(X;Y)还满足下式：

三、基于核函数和标记权重的特征选择模型

（一）RBF核函数。在实际情况中，分类函数是非线性的，无法将原始特征空间中的数据集进行区分开。因此，通常需要用一种非线性映射的方法将原始特征空间映射到高维空间中,使得特征在高维空间中线性可分。

假设f∈Rm经过非线性函数φ(f)转化为φ(fi)∈Rd,d>m，其中，fi所属的m维空间为变换前的特征空间，φ(fi)为变换后的特征空间。假设算法中的各矢量间的相互作用在高维空间中进行内积运算，可能由于维数过高导致无法得出计算结果。为解决该问题，只需找到一个合适的函数，使其满足K(xi,yj)=φ(xi)·φ(yj)，这就可以用原空间中的内积函数进行高维度的内积运算。这就避免了维度灾难带来的计算难题，还能使得特征空间中的特征变得可分。核函数就是这一思想的体现。在本文算法中，是利用径向基核函数（RBF）核函数对特征空间进行处理，接下来将介绍RBF核函数：

径向基核函数（RBF）：

RBF核函数可以将特征空间映射到更高维的特征空间中，另外，函数的复杂程度直接受核函数参数的个数的影响，而RBF所需的参数个数少。而且RBF核函数具有局部性核函数的学习能力[16,17]。因此，本文利用RBF核函数对特征空间进行处理。

（二）标记权重。在已有的多标记特征选择算法表明考虑标记空间隐藏的信息能有效提高多标记学习精度。每个标记对样本的重要性都不同，为此，在本文算法中，根据每个标记下所含该标记的样本数量对标记进行赋予权重。

给定样本X={x1,x2,...,xq}，标记空间L={y1,y2,...ym}，对于标记yi的权重计算如下：

式（5）中，q表示样本大小，计算每个标记下含有该标记的样本数量所占比例，以此给该标记赋予权重，不含该标记的权重都视为1。

（三）KF-LW模型。在本文所提出的基于核函数和标记权重的多标记特征选择算法中。首先，针对每个标记，统计含有每个标记的样本数量，对标记进行赋权重；然后，用RFB核函数将特征空间映射到一个更高维的特征空间，在这个新的特征空间中，计算特征与标记空间之间的互信息，根据计算所得的信息熵值对特征进行排序；最后，选取特征总数的百分之二十的数量构成最终特征子集。

根据上述描述，基于核函数和标记权重的多标记特征选择算法(Multi-feature selection based on kernel function and label weighting)描述如下：

A l g o r i t h m：K F-L W输入:X:样本集;特征集合：F={f 1 },f 2,...,f m，标记空间：Y={y 1,y 2,...y n}，k k：特征子集大小输出S:已选特征子集1)2)3)4)5)6)7)8)9)1 0)1 1)S=∅；重复;f o r i=1:n统计每个标记下，含有该标记的样本数量；根据式（5）计算每个标记赋权重；e n d根据式（4）将原始特征空间映射到高维空间中；f o r i=1:m根据式（3）计算特征与标记空间之间的互信息；e n d根据互信息值对特征进行排序；选取前k k个特征作为最终的特征子集

四、实验结果及分析

（一）实验数据集。为了验证KF-LW算法的有效性，本文选取了6个数据集进行实验验证，所有数据集均能从http://mulan.sourceforge.net/datasets.html.下载，表1为各数据集的详细信息。

表1 多标记数据集

（二）实验结果及分析。本文的实验是分别选取了KELM和MLKELM作为分类器，正则化系数为1，核函数选择RBF。本文选择 One Error(OE),Coverage(CV)，Ranking Loss(RL)和Average Precision(AP)这4个评价指标[11]检测分类性能。对比算法有基于多变量互信息的多标记特征选择算法（PMU）、基于最大相关性降低多标记维度（MDDMopt，MDDMproj）[16]。实验对比过程中，对比算法与本文算法均采取相同分类器。所有算法都选取特征总数的20%作为最终特征子集数。表中↑表示指标数值越大越好，↓表示指标数值越小越好，黑体字表示各数据集在各个算法上取得的最好结果，各实验结果后面“（）”内的值表示各数据集在各算法上的排序。

表2 在平均精度上五个特征选择算法的排名

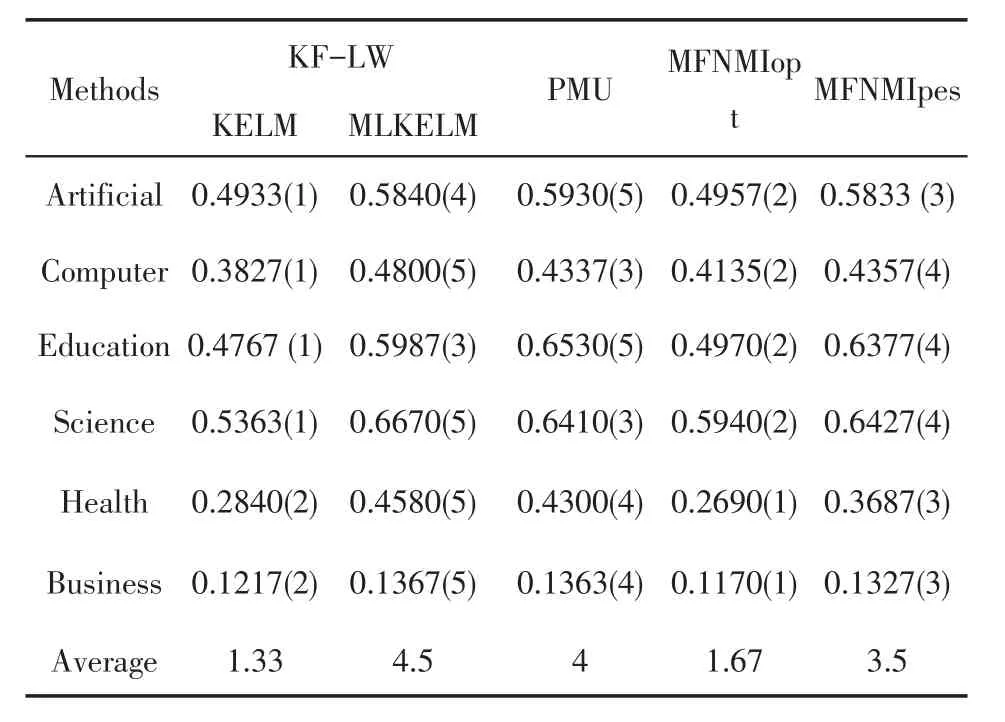
表3 在1-错误上五个特征选择算法的排名

表4 在排位损失上五个特征选择算法的排名

表5 在覆盖率上五个特征选择算法的排名

分析实验结果可知：

1）表2实验结果表明：在6个数据集上，KF-LW在5个数据集上获得最大Average Precision值，即性能最优。在Health数据集上，算法MFNMIpes获得最优Average Precision值，KF-LW(KELM)取得的Average Precision值与最优仅相差0.0006。在8个数据集上的平均排序结果可以看出，KF-LW(KELM)排第一。

2）在表3中，本文算法与MFNMIopt、MFNMIpes和PMU这几个对比算法的实验结果表明，有4个数据集上KF-LW(KELM)算法的One-Error值都是最小的，这表明算法KF-LW的性能很好，在One-Error指标上，KF-LW(KELM)排名第1。

3）从表4所有算法的Ranking Loss值可看出：本文算法KF-LW与几个对比算法相比，在6个数据集上KF-LW取得的Ranking Loss值都最小。其中，KF-LW(KELM)算法在4个数据集上取得最优值，KF-LW(MLKELM)算法在2个数据集上取得最优值。在6个数据集上的综合排位中，KF-LW(KELM)排在第1。

4）根据表5可看出：本文所提的算法KF-LW在6个数据集的 Coverage值最小。在 Artificial、Education、Health 和Business这4数据集上，算法KF-LW(MLKELM)的Coverage值均排第一位，在Computer和Science这两个数据集上，KF-LW(KELM)的Coverage值排在第一位。

5）从以上实验结果和算法的排序可看出，本文所提算法在Average Precision、Ranking Loss和Coverage这三个评价指标上效果都优于对比算法。综合排位中，本文算法均排在第一位，这进一步表明本文算法的有效性。

五、结语

本文所提的基于核函数和标记权重的多标记特征选择算法，利用核函数将原特征空间映射到高维空间，使得特征具有可分性，并根据标记空间的信息对标记进行权重赋值，最后根据信息熵度量特征与标记空间之间的相关性，实验结果表明KF-LW能有效提高分类器预测的分类性能。