变电站构架避雷针风振响应分析
2020-11-12董新胜张军锋管品武
董新胜 张军锋 杨 洋 管品武
(1.国网新疆电力公司电力科学研究院,乌鲁木齐830011;2.郑州大学土木工程学院,郑州450001)
0 引 言
变电构架是变电站的标志,其数量多,高度大,形式复杂多样,尤其对于高压变电站。为避免雷击现象,变电构架上往往安装避雷针,以保护变电设备。避雷针结构属于典型的高耸结构,风振效应较为显著,并且偶有破坏事故发生[1-4],因此变电构架避雷针的风振效应研究备受关注[5-6]。并且为得到变电构架避雷针的风致内力,往往采用时域法进行动力计算。
以新疆某特高压变电站的单跨和三跨构架避雷针结构为例,在前期结构检测工作的基础上,进行结构表面脉动风场模拟和风振响应时程计算,分析了构架避雷针的风振响应特点以及风向和场地紊流度对风振响应的影响,为结构设计提供了参考。
1 工程背景及计算模型
所选两例构架避雷针结构位于新疆某750 kV变电站(图1)。单跨构架避雷针结构高50 m,由底部人字柱塔架和上部变截面钢管避雷针组成,其中右侧人字柱塔架设有端撑以增加平面内刚度,两侧避雷针均由3 段变截面的钢管连接而成且结构尺寸相同。两侧塔架之间采用三角形截面形式的格构式横梁连接,横梁高度和底宽均为2.4 m,采用角钢拼接而成。三跨构架避雷针形式与单跨近似,只是结构高度为47 m,并且左侧2#塔架有所加强以提高平面内外刚度。两种结构均采用钢构件(表1),塔架下部构件为Q345 钢材,上部避雷针为Q235钢材,格构式横梁弦杆和腹杆分别为Q420和Q345钢材。
采用ANSYS 建模计算,除格构式横梁采用Link8单元外,其他杆件均采用Beam188单元。格构式横梁中弦杆和腹杆的连接视为铰接。横梁两端与塔架连接方式如图2(a)所示,横梁下弦杆和端腹杆通过螺栓与塔架钢板连接。因整体结构受力类似于空间排架,故此连接形式一般视为铰接[7-8]。但为计入横梁传递荷载对塔架的扭矩效应,在整体建模的过程中模拟了横梁和塔架的连接节点板,并选取了两种方法来模拟,即:分别采用Shell181 单元和Beam188 单元模拟节点板,并在横梁各杆件端点位置设置节点以完成单元划分。经对比,两种方法所得结构前三阶的频率基本相同,误差在1%以内;X 向和Y 向静风荷载作用下两种方法所得避雷针顶点处的位移也基本相同,误差也在1%以内。下文采用第二种方法以方便计算。
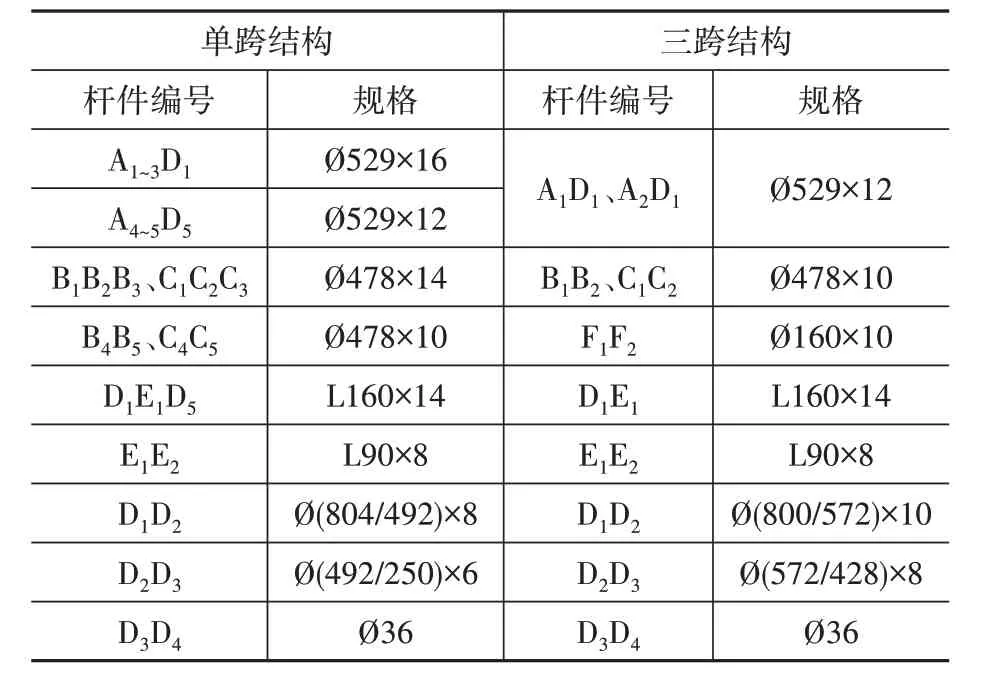
表1 两个结构的杆件规格Table 1 Component sizes of the two structures mm
从表2 所列结构前10 阶的模态特征可以看出,单跨结构低阶振型往往表现为两侧避雷针在X 向和Y 向的弯曲振型,且频率较为接近,因为上部避雷针作为独柱悬臂构件,抗弯刚度较低;后续振型则以结构的扭转振型为主,因为平面结构的整体抗扭刚度偏低。三跨结构的振型同样以各避雷针及塔架的弯曲振型为主,同时伴随一定的横梁弯矩,但因结构总体跨度更大,扭转振型已难以激发。另外,两种结构计算所得基频与现场实测数据1.456 Hz和1.563 Hz吻合良好。
结构的振型模式较为复杂(图3、图4),但对塔架避雷针风振效应有贡献的主要为塔架自身X向和Y 向弯曲振型,对于单跨结构也即前四阶振型。需要注意的是,两种结构在Y 向的前两阶频率基本一致,但共振效应却有明显差异,详见下文。
2 计算方法
结构处于A 类场地,基本风压0.8 kPa,由此得场地10 m 高度风速U(10)=42 m/s。由于避雷针等构筑物的设计控制指标为内力而非位移,故为得到内力的动力响应而采用时程计算。首先依Davenport 谱和A 类场地参数[9-10]如风剖面幂指数α=0.12,10 m 高度紊流度I10=0.12和地面阻力系数κ=2.4×10-3,采用谐波叠加法进行脉动风场模拟[11-12](注:谐波叠加法原理和实现过程以及Davenport 谱和相干函数参数详见文献[12],文献[12]也作为附件以便审阅),再由准定常气动力假定得各节点脉动风荷载时程(式(1))。另外,为分析场地类型的影响,还以B 类场地参数进行了风场模拟和结构计算。
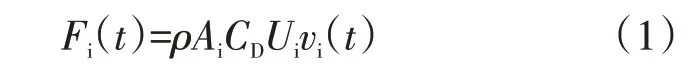
式中:i为加载点编号,空气密度ρ=1.25 kg/m3,阻力系数CD依规范[16]取0.6;Ai为加载点迎风面积,加载点位置设置如图5所示。
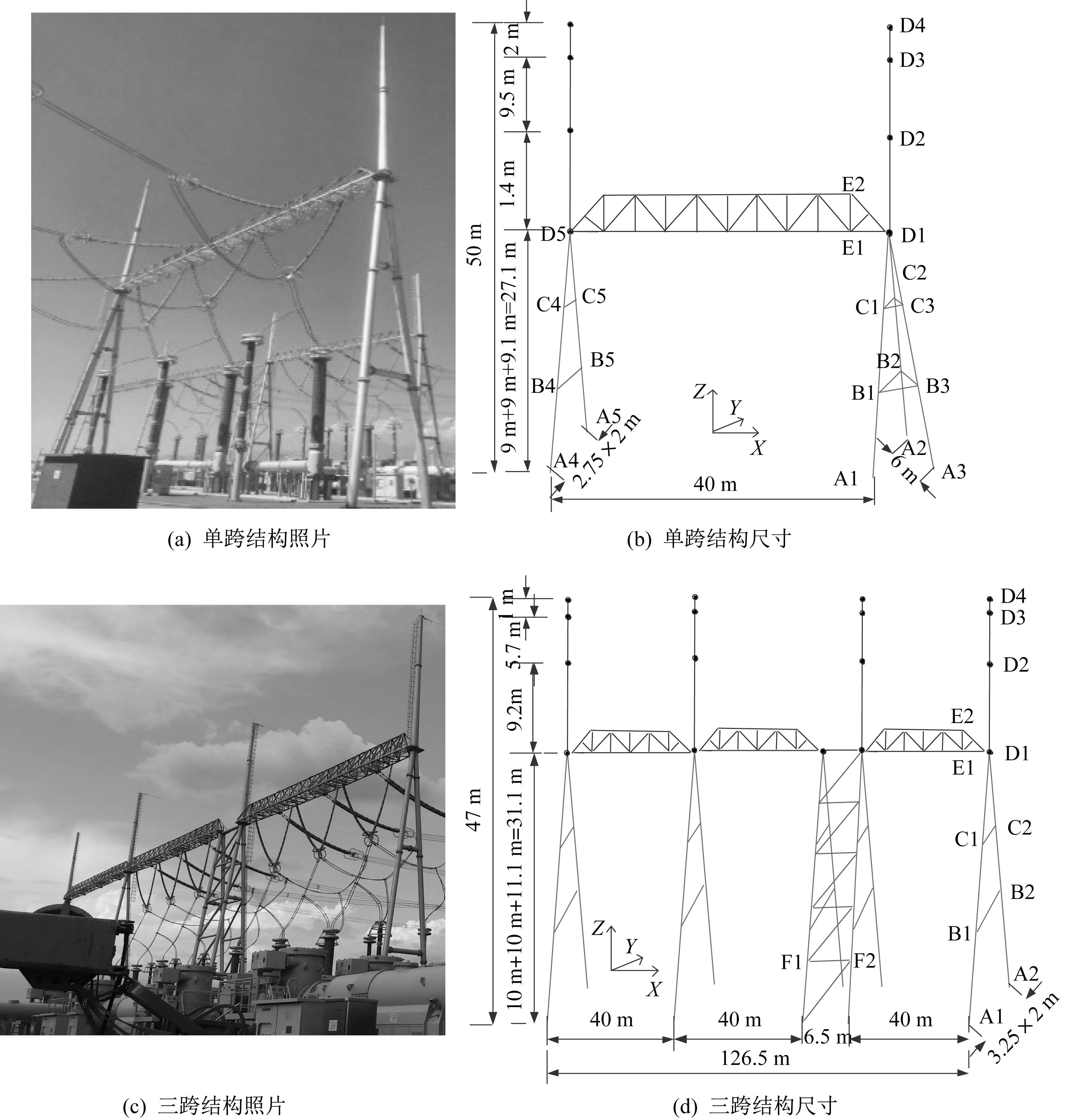
图1 避雷针结构形式Fig.1 Prototypes of the lightning rods
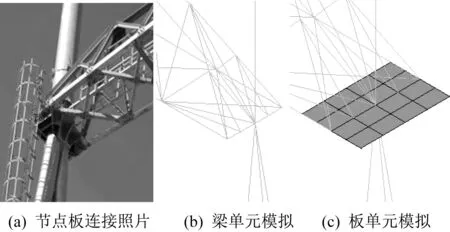
图2 局部连接形式及有限元模拟Fig.2 Local connection and its simulations
对于横梁荷载,认为其仅受Y 方向的风荷载,或者可写为
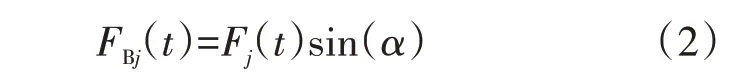
式中:j 为横梁加载点编号(图5);FBj(t)为横梁Y向荷载;α为风向,沿X方向为0°,沿Y向为90°。
脉动风模拟采用单索引频率[13-15],根据文献[12]所给模拟参数取值原则以及试算,取频率上限fu=4.5 Hz和时频点比值M/N=2,即时间步长Δt=1/9 s,以使后续动力计算中能充分计入结构的共振效应;模拟周期T0=600 s,共计5 400 个时间点。图6 给出了目标谱与模拟所得四个高度脉动风速样本风谱,可知模拟效果良好。
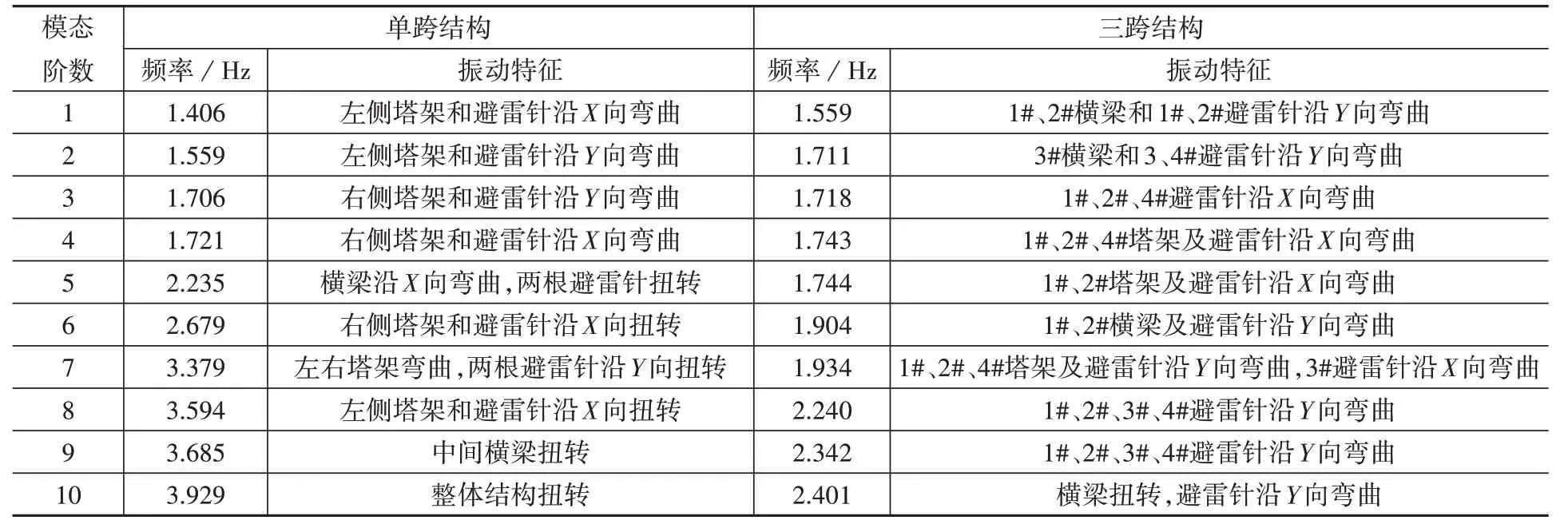
表2 两个结构的模态特征Table 2 Modal characteristics of the two structures
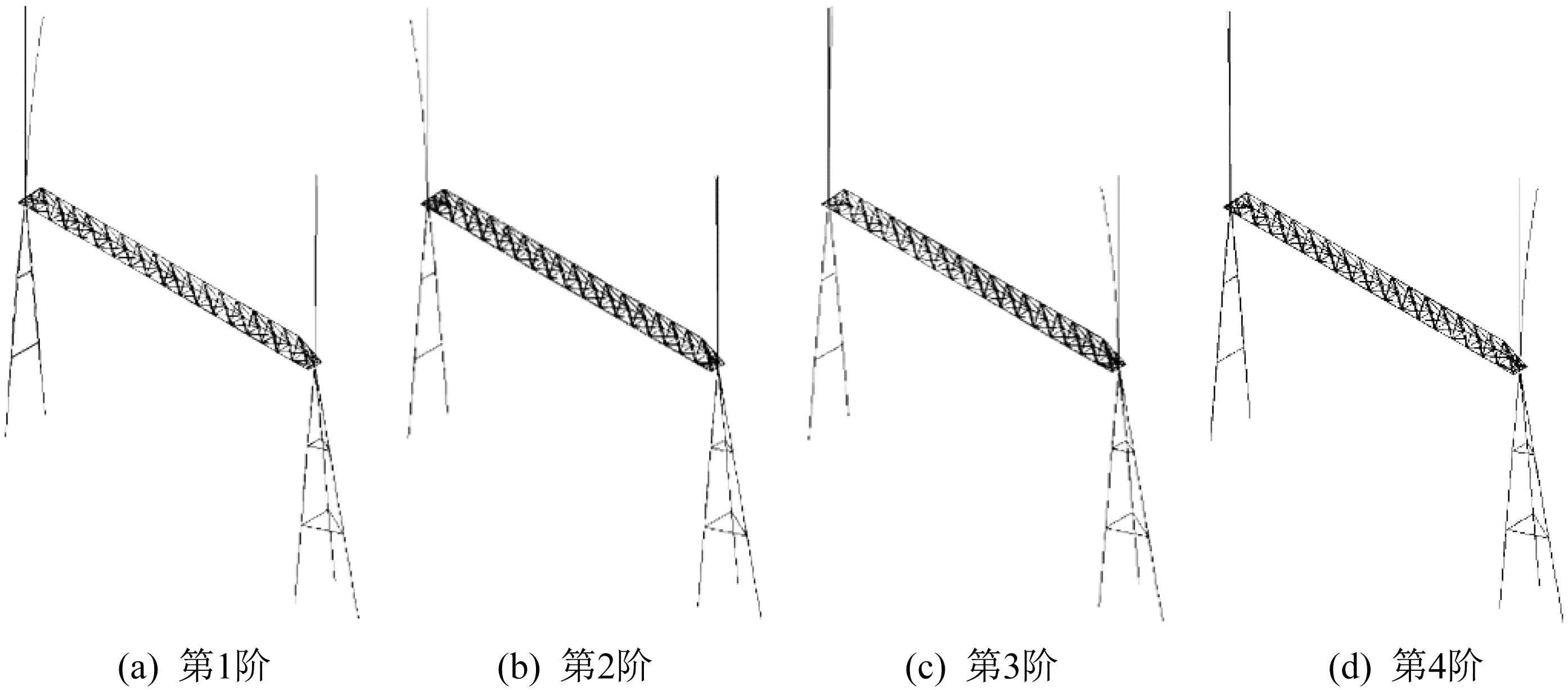
图3 单跨结构侧弯振型Fig.3 Bemding modes of the single span structure

图4 三跨结构侧弯振型Fig.4 Bemding modes of the triple span structure
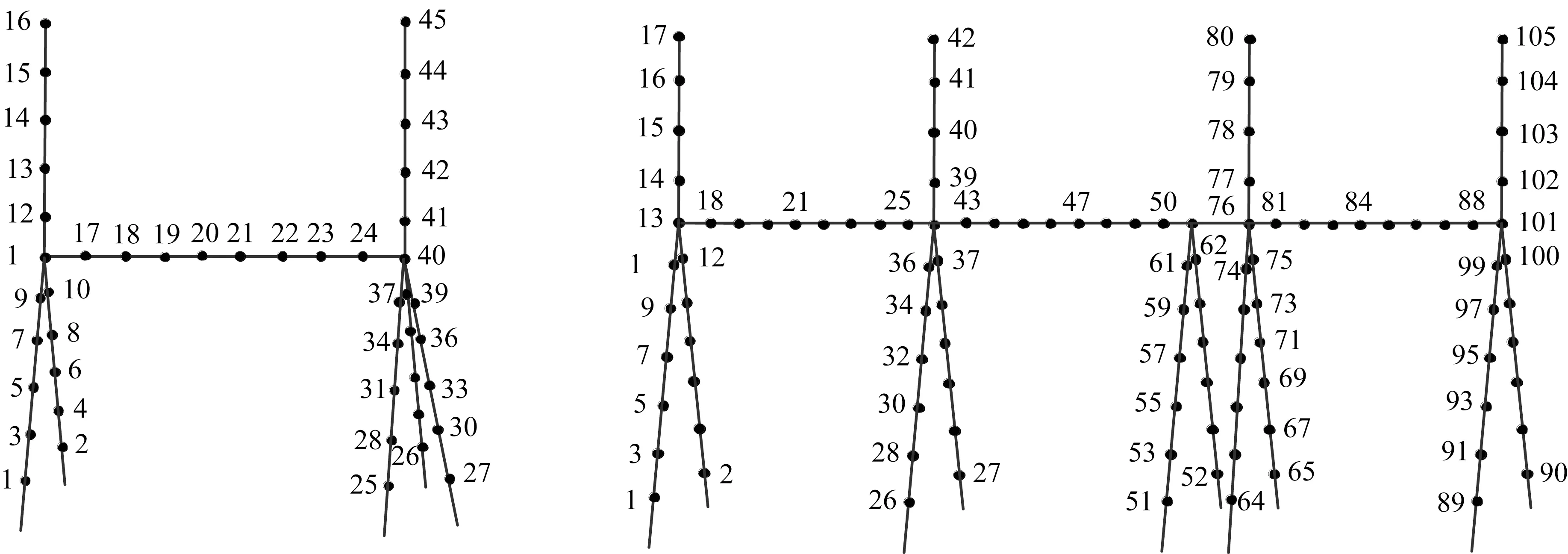
图5 加载点位置示意图Fig.5 Depiction of the wind loaded locations
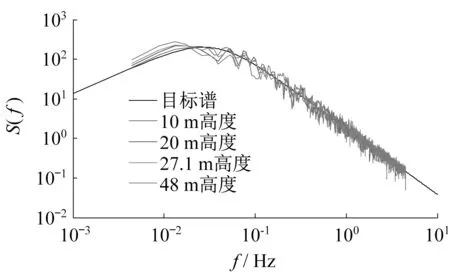
图6 目标谱与模拟所得四个高度脉动风速样本风谱Fig.6 The target and simulated wind spectrums for four locations
动力计算在ANSYS 中采用隐式的Newmark直接积分法进行,所加风载为包括平均和脉动风载的完整风荷载,脉动荷载的每个时间步长Δt对应ANSYS 求解中的一个荷载步。为充分计入共振效应,每个荷载步分为4 个子步,即积分步长ITS=1/36 s。为保证计算的精度,本文采用了ITS=1/72 s 进行对比计算。结果表明,两者计算结果基本一致,这也说明计算中所考虑的时间步长是合理的。在动力计算中,所施加的荷载为包含平均荷载的总脉动荷载,故去除掉前60 s 的响应以消除突风效应的影响[17]。采用瑞利阻尼,对前两阶频率取阻尼比ζ=1%。
采用阵风响应因子G(式(3))表示风振效应,并区分位移U、弯矩M和剪力F分别给出。
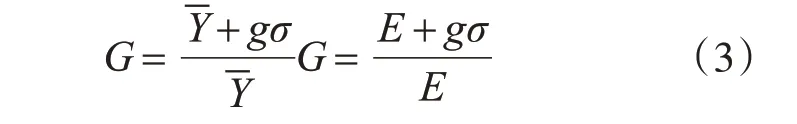
式中:E 和σ 为响应均值和根方差;峰值因子g=3.5。
3 风振响应分析
3.1 风向影响
从结构形式可知,不管是单跨还是三跨结构,避雷针的位移均值和根方差都将受到下部塔架荷载的影响,其内力均值仅与自身荷载有关而根方差同样会因共振效应的参与而受下部塔架荷载的影响。
因单跨结构左右避雷针的风振特点类似,并且各避雷针弯矩和剪力的风振响应沿高度分布模式类似,故图7 主要给出了左侧避雷针各风向下的位移和弯矩响应,同时给出了右侧避雷针0°和90°风向下的结果。可以看出,左侧避雷针的位移均值EU随风向角的增加而增加,且0°风向下的EU明显偏小。因各工况下整个高度内的位移偏差基本一致,故可通过横梁与塔架交点也即D5位置的位移对此进行分析。

图7 单跨结构避雷针响应Fig.7 Wind responses of the single span structure
需要强调,左侧避雷针0°风向下的EU小于90°风向下的结果,并不是因为0°风向下也即平面内刚度更大,而是90°风向下存在横梁荷载且其引起的位移更大(表3)。由表3 可知:①即使90°风向下没有横梁荷载,D5 的Y 向位移将略小于0°风向下的X向位移,说明对左侧塔架来说,其平面外刚度较平面内刚度略大,这在表2 所列左侧塔架前两阶模态及频率值亦可证实;②在90°风向下,横梁荷载在D5点引起的位移与塔架和避雷针荷载引起的位移相当,而不同风向角下横梁风载逐渐增加且塔架和避雷针风载不变,故避雷针位移随风向角的增加而增加。
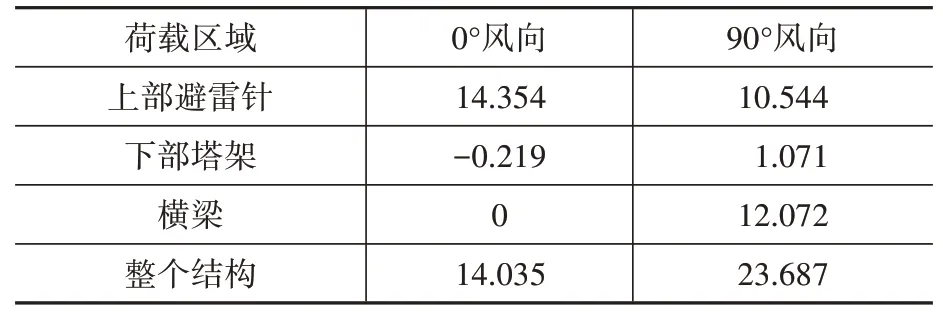
表3 局部荷载作用下D5位置的位移Table 3 Displacements at point D5 under local loads mm
对于左侧避雷针的位移根方差σU,因0°风向结构刚度较弱,90°风向荷载脉动性较大,结构刚度和荷载的共同影响使得两种风向下σU较为接近且以0°风向略大;另外三个风向因横梁荷载偏小,故σU略小;再考虑各风向下的EU可知90°风向为最不利风向。四种风向下避雷针上作用的荷载一致,故四种风向下的内力均值EM和EF相等。对于σM和σF结果,依然为90°和0°较大而其他三个风向的最小。
综合可知,对于单跨左侧避雷针,90°风向对位移和内力来说均为最不利风向,并且对于单跨右侧避雷针和三跨的各个避雷针均有相同的结论,故下文主要以90°风向进行分析。由于0°风向下结构受力模式和荷载与90°风向完全不同,同样也给出0°风向的结果。
另外,对比左右两侧避雷针结果可知,由于右侧塔架端撑的存在,右侧避雷针的EU明显偏小,两种风向下其D1 位置位移约为左侧D5 位置的75%;同时由于端撑使刚度及频率增加,两种风向下右侧避雷针σU的背景及共振分量也都较左侧减小,尤其以0°风向下最为显著,这也是因为0°风向下右侧避雷针的刚度及频率较左侧的增加更为显著(表2)。由于内力的均值和根方差主要由避雷针自身荷载决定,故左右两侧避雷针内力响应的均值和根方差均基本一致。
3.2 阵风响应因子
图8 和图9 分别给出了单跨结构和三跨结构的阵风响应因子G。由于避雷针顶部内力幅值较小,故仅给出下半区段的G值。对于单跨结构,从图8可以看出,除左侧避雷针的GU外,其他响应均为90°风向的G 值更大,这也印证了前文90°风向为最不利风向的结论;而左侧避雷针的GU在0°风向较90°风向明显偏大的原因是因为0°风向下的EU偏小,且两个风向的σU较为接近;右侧避雷针两个风向下GU较为接近的原因是其90°风向下的EU和σU均较0°风向偏大(图7)。
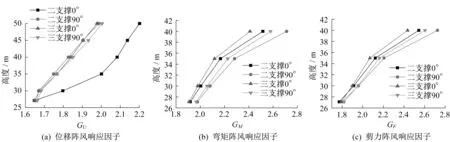
图8 单跨结构阵风响应因子Fig.8 Gust response factors for the single span structure
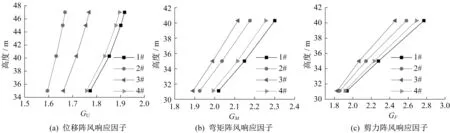
图9 三跨结构90°风向阵风响应因子Fig.9 Gust response factors for the triple span structure in Y direction
需要注意的是,对于单跨和三跨结构的Y 向,其前两阶频率是相同的(表2、图4),但单跨结构各响应的G 值却明显大于三跨结构,说明前者的共振效应更为显著,这在图10 中有直观体现。说明不同结构在频率相同时,由于各自振型的差异,其共振效应亦会有明显差异。另外,从图10 可以看出,尽管三跨结构的一阶共振效应相对单跨结构偏小,但两种结构各工况均以一阶共振为主,故在分析时可仅关注其一阶模态,这也证明了前文脉动风模拟所取fu=4.5 Hz是充分的。
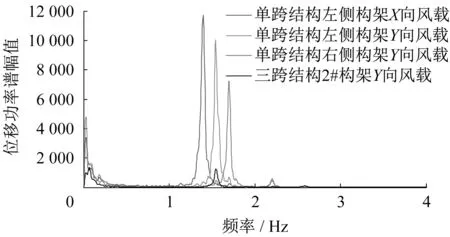
图10 代表性工况的顶点位移功率谱Fig.10 PSD of top displacement for representative conditions
从图8和图9还可看出,不管是单跨还是三跨结构,其阵风响应因子G 均表现出以下3 个规律:①各响应的G 均沿高度的增加而增加,并以GM和GF的增加最为明显,GU沿高度相对较均匀;②从幅值上看,GM和GF较为接近且明显大于GU,说明传统以位移为指标进行等效风荷载分析确定的风振系数取值会低估结构实际的内力响应,应以内力为指标进行分析,又因钢管结构在设计时的弯矩较剪力更为关注,故可直接取弯矩作为风振系数评价指标;③90°风向下的GM和GF已明显超过现行《变电站建筑结构设计技术规程》[16]的风振系数取值β=2.0,并以单跨结构最为显著,说明现行规程的取值偏不安全,应考虑结构特性和风向给出更为合理的β取值。
根据图8 和图9 的GM分布和风振系数β 取值原则,可得每个避雷针的β值(表4)。即使在A 类场地,各避雷针风振系数的确已超过2.0。如果变电站位于B类场地,因场地紊流度的提高,风振系数将进一步增加。
4 结 论
为明确变电站避雷针结构的风振响应特点以及风振系数取值,以两座构架避雷针结构为例,进行了多风向和多场地类型的风振响应时程计算和风振系数分析,主要结论如下:
(1)对于构架避雷针结构,由于端撑的存在,其平面内外刚度相当,双向基频也基本一致,但由于平面外也即90°风向下横梁将承受较大荷载且会传递至避雷针塔架,故90°风向是其最不利风向。
(2)由于结构基频较低,构架避雷针的风振效应较为显著,尤其是单跨结构,其共振响应与背景响应基本相当;三跨结构基频虽与单跨结构基本一致,但其共振效应较为有限,这也说明不同结构的风振效应大小不能完全根据基频判断,还应考虑各自模态的特点。
(3)避雷针结构设计中,内力较位移响应更受关注,且内力的风振效应较位移更大,因此应采用内力作为风振系数的评价指标。由于弯矩和剪力的风振效应基本相当且弯矩在结构设计中更受关注,故应取弯矩作为评级指标。
(4)为便于工程参考和应用,给出了两种场地类型以弯矩作为指标所得各避雷针的风振系数取值。即使在A 类场地,各避雷针风振系数取值均在2.0 以上,说明现行规程的风振系数取值偏低。
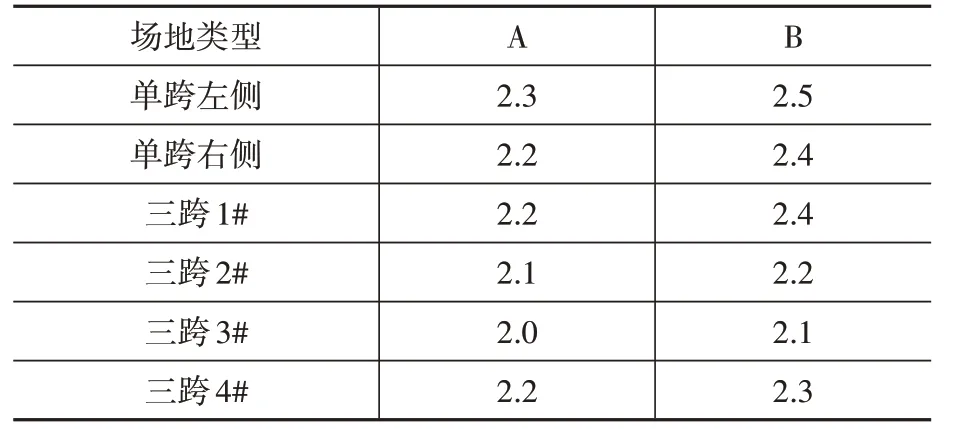
表4 避雷针风振系数取值Table 4 Load amplification factors for different rods
