受电弓等效参数识别及结构强度研究
2020-11-11王俊勇辜晨亮
贾 荣,王俊勇,辜晨亮
(1 北京中车赛德铁道电气科技有限公司,北京 100176;2 西南交通大学 机械工程学院,成都 610031)
受电弓是位于电力机车和动车组车顶的受流装置,是网线将电能传输到车辆的唯一途径。机车车辆的正常运行离不开受电弓的稳定受流,受电弓的稳定受流主要取决于受电弓的动态性能和自身结构强度,而且受电弓等效参数是反映受电弓动态性能的重要参数[1],等效参数的识别可以为弓网动力学研究提供基础。
考虑受电弓上导杆和弓头的运动,建立受电弓机构的平面运动数学模型,对受电弓框架归算质量、等效阻尼和弓头等效刚度进行计算。基于相关弓网标准,对受电弓结构静强度进行分析,并计算分析受电弓焊缝疲劳强度,为今后受电弓结构优化提供理论依据。
1 受电弓力学模型
DSA200型受电弓为气囊式受电弓,主要结构见图1。该型受电弓工作原理为:在升弓时,气囊通过钢丝绳产生升弓力矩,使得下臂绕长轴转动,通过下臂、下导杆、上臂和上导杆组成的连杆机构将下臂转动转化为弓头垂向运动;在降弓时,气囊排气,受电弓依靠部件自身重力下降到落弓位。
受电弓的力学模型主要包括:多刚体模型、归算质量模型、刚柔混合模型和全柔模型[2];由于归算质量模型具有较高的计算效率和计算精度,所以这类模型使用最广泛。
以2质量模型作为DSA受电弓的力学模型,如图2所示,m1、k1、c1分别为弓头的归算质量、等效刚度和等效阻尼;m2、k2、c2分别为框架的归算质量、等效刚度和等效阻尼。一般来说,弓头归算质量m1为弓头自重,弓头等效阻尼c1趋近于0;受电弓静态接触力为定值的特性使得框架等效刚度k2的理论值为0,由于关节摩擦力和气囊的存在,经验值一般取70 N/m。所以,只需要计算出k1、m2和c2的值就能得到DSA2000受电弓2质量模型的等效参数。
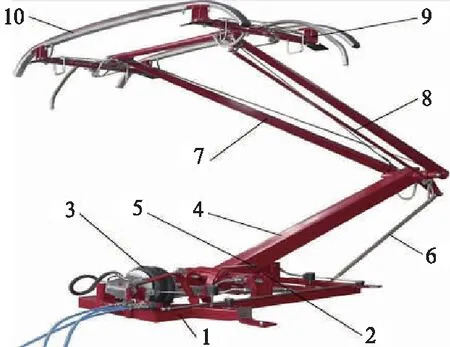
1-底架; 2-阻尼器; 3-气囊; 4-下臂;5-弓头缓冲器; 6-下导杆; 7-上臂;8-上导杆; 9-弓头; 10-碳滑板。图1 DSA200受电弓
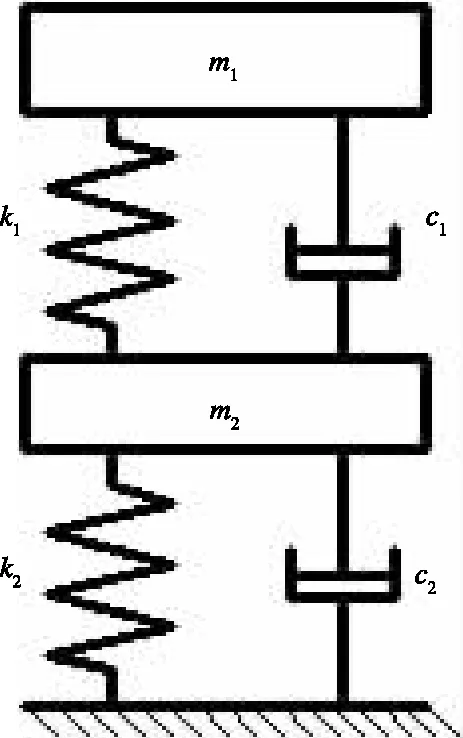
图2 受电弓2质量模型
2 受电弓等效参数识别
2.1 杆件运动方程
考虑上导杆、弓头和阻尼器的运动,将各部件视为杆件,得到受电弓平面运动模型。如图3所示,AD、BC、CE、FG、EF和HI代表下臂、下导杆、上臂、上导杆、弓头和阻尼器;Q1~Q5分别代表各主要部件质心;α、β、γ、λ、μ分别表示下臂、下导杆、上臂、上导杆和弓头与水平线之间的夹角。
以下臂转角α为自变量,由受电弓各杆件位置关系可得B、D的距离为:
(1)
根据余弦定理求得∠CBD、∠ABD、∠BCD和∠AD,下导杆转角β与上臂转角γ分别为:
β=π-∠CBD-∠ABD-ε
(2)
γ=∠CBD+∠BCD-∠ADB-α-δ
(3)
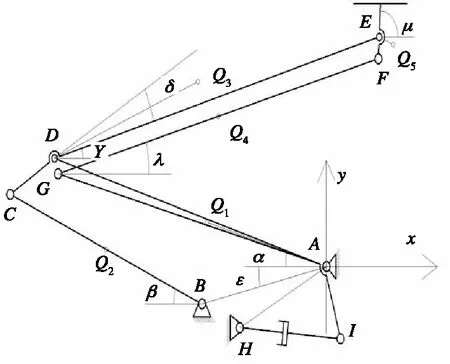
图3 受电弓平面运动模型
E、G两点的坐标分别为:
(4)
(5)
上导杆转角λ为:
(6)
弓头转角μ为:
(7)
受电弓工作高度H为:
H=YE+540
(8)
令AH连线与x轴负方向的夹角为θ,根据余弦定理,可得阻尼器长度S为:
2lAHlAIcos(∠BAI-θ-α)
(9)
根据DSA200各部件参数,可以得到在升弓过程中各主要部件角度以及阻尼器长度与下臂转角的关系,如图4、图5所示。根据计算结果可知,在升弓过程中,只有下导杆转角β和阻尼器长度S与下臂转角α与较好的线性关系,而上臂、上导杆、弓头的转角γ、λ、μ与下臂转角α为非线性关系。
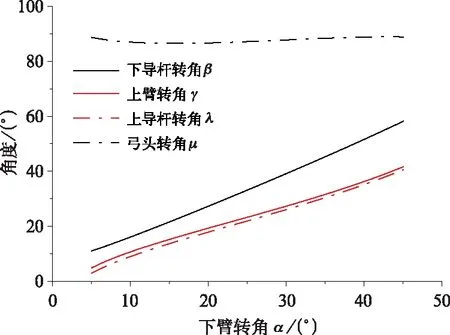
图4 主要部件转角与下臂转角的关系
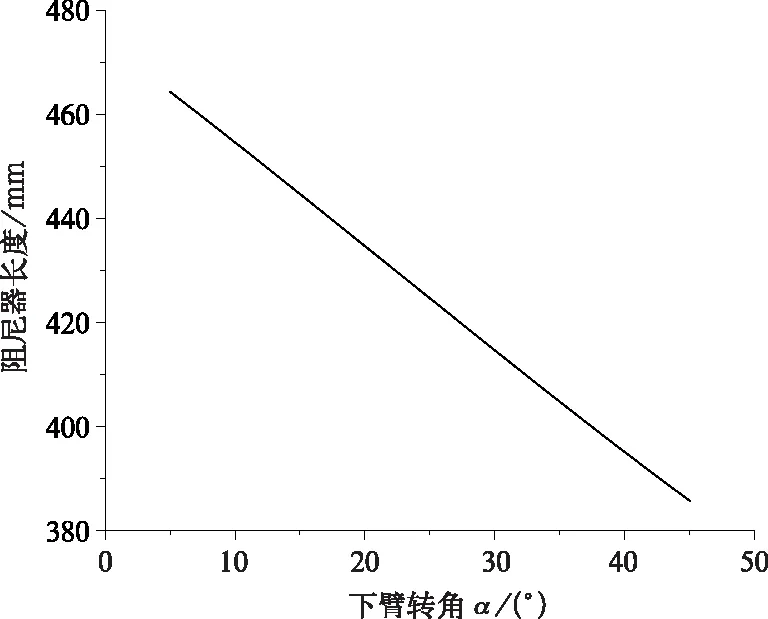
图5 阻尼器长度与下臂转角的关系
2.2 框架等效参数计算
(10)
(11)
(12)
(13)
同理可得:
(14)
(15)
根据文献[3]对受电弓各部件动能T的推导和动能能等效原理,可得框架归算质量为:
(16)
根据阻尼器耗散能等效原则,可得框架等效阻尼为:
(17)
DSA200工作高度在1~3 m范围内,结合式(1)~式(17)以及各部件结构参数,可以得到受电弓在不同工况下,框架归算质量、框架等效阻尼的值,如图6和图7所示。从计算结果可得,框架归算质量与工作高度为正相关,在1~3 m的工作高度范围内,框架归算质量的值在9.5~13.9 kg范围内。框架等效阻尼在1~2.4 m范围内与工作高度正相关,在2.4~3 m范围内与工作高度负相关。
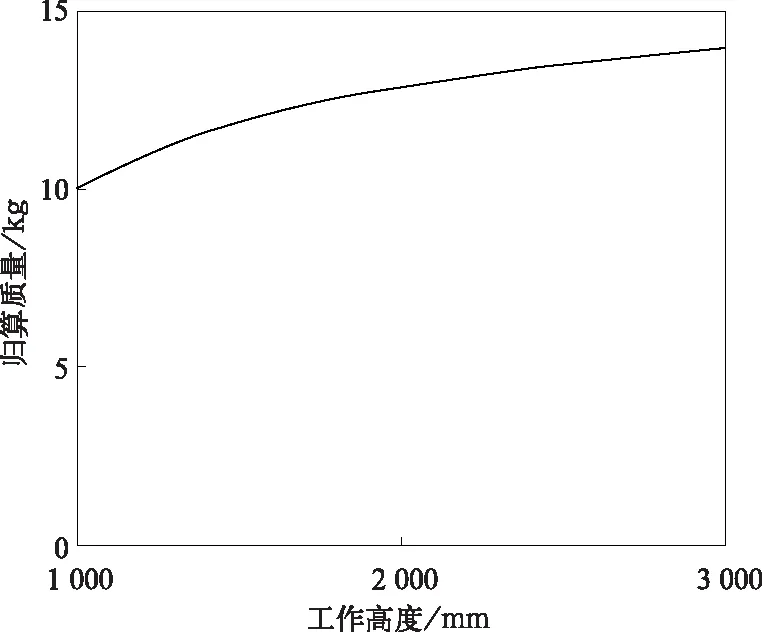
图6 受电弓框架归算质量
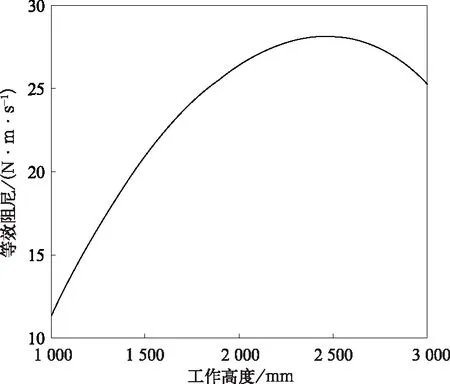
图7 受电弓框架等效阻尼
根据式(10)~式(16),还可以得出各个部件对框架归算质量的影响,如图8所示。上、下导杆在框架归算质量中的占比很小,而上臂、下臂和弓头支撑对框架归算质量的贡献较大,所以在今后受电弓参数优化中,应该把 弓头支撑、上臂和下臂作为主要对象。
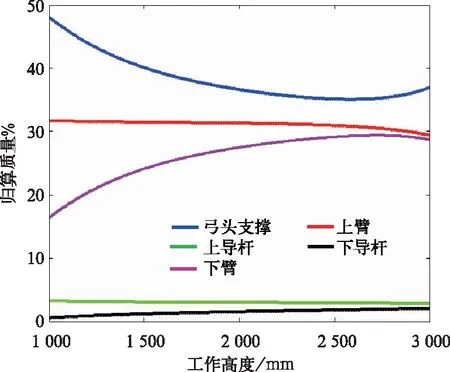
图8 各部件对框架归算质量的影响
2.3 弓头等效刚度计算
DSA200弓头弹簧两端分别与弓头支撑和铝支架铰接,铝支架通过螺栓连接支撑碳滑板。根据弓头结构建立弓头等效刚度计算模型,见图9,其中lAB、lCD表示弹簧长度,lBC表示铝支架,θ表示弹簧与水平方向的夹角。
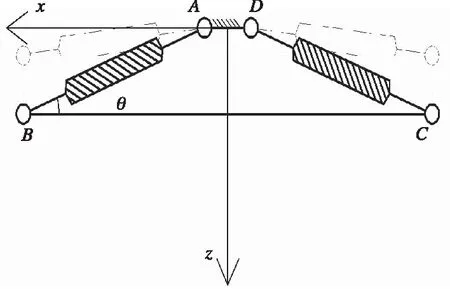
图9 弓头弹簧计算模型
设弹簧原长为l0,弹簧刚度为k0,由于弓头限位结构的存在,使得铝支架在z方向的运动范围为[24,89],相对应的碳滑板的垂向位移范围为0~65 mm。以BC与AD的距离为自变量,根据几何关系可得:
(18)
弹簧对铝支架的作用力在z向的分量Fz为:
Fz=2k0(lAB-l0)sinθ
(19)
DSA200弓头为4根弹簧的对称结构,等效刚度keq为:
(20)
联立式(18)~式(20)可得,弓头等效刚度取决于铝支架的垂向位置,如图10所示。弓头等效刚度呈非线性,其大小随铝支架在z向位移的增加而增加,在铝支架垂向有效活动范围内,弓头等效刚度的值在4 019~8 981 N/m之间。
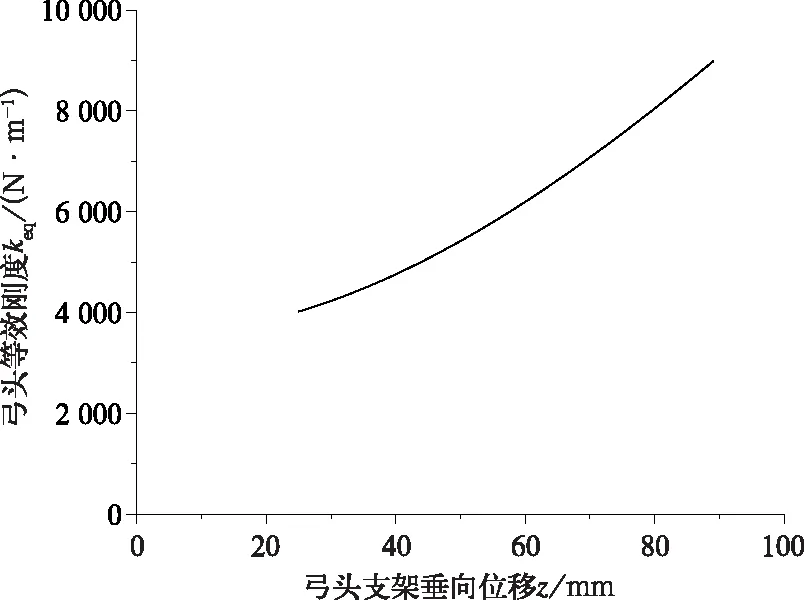
图10 DSA200弓头等效刚度
结合2.1~2.3节的计算分析结果,得到工作高度1.9 m时,DSA200受电弓2质量模型的等效参数,见表1。
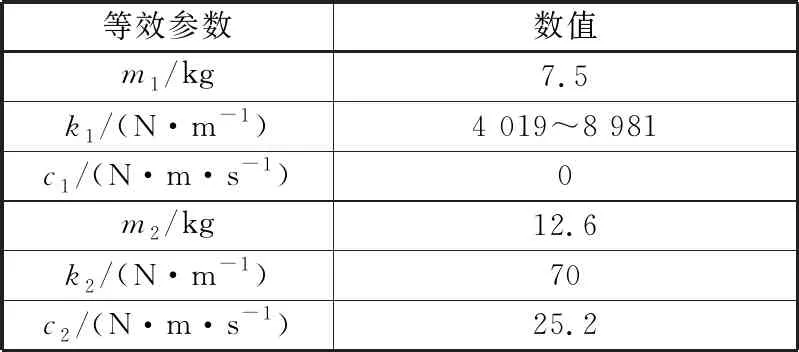
表1 DSA200等效参数
3 结构强度计算分析
根据相关弓网标准,利用有限元软件,对DSA200受电弓的静强度和疲劳强度进行校核。
3.1 有限元模型及边界条件
利用Hypermesh将受电弓三维模型离散为包含184 692个节点和216 768个单元的有限元模型,并赋予主要部件相应的材料属性,底架和下臂材料分别为碳钢和不锈钢,上臂和弓头支架为铝合金,受电弓3个底架安装座添加固定约束,如图11所示。
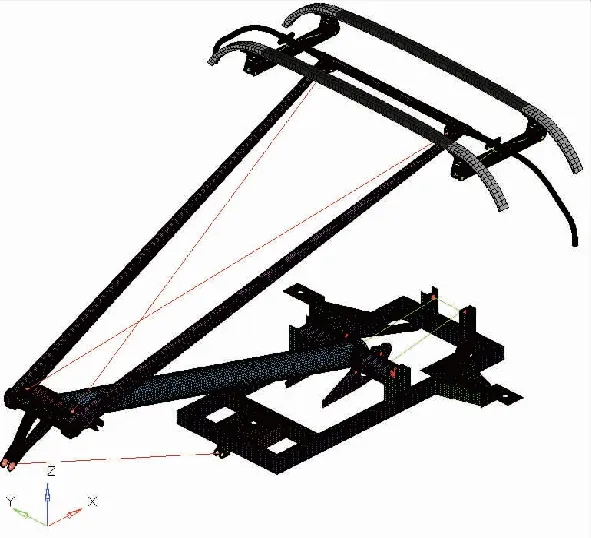
图11 DSA200有限元模型

表2 静强度计算载荷工况 N
受电弓运行时,主要承受空气阻力和弓网接触力的共同作用,根据TB/T 3271-2011[4]和EN 50367[5],并结合DSA200运行方向、弓网接触力作用点的位置和空气阻力与受电弓迎风面积的关系,得到DSA200受电弓的静强度载荷工况和疲劳载荷工况,分别见表3和表4。
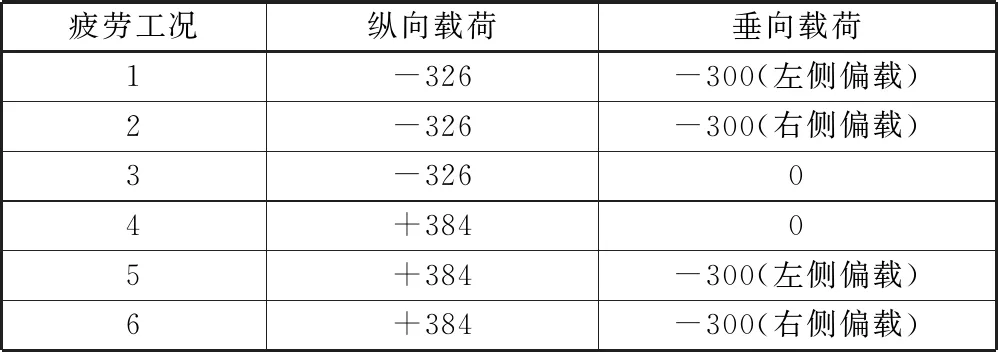
表3 疲劳强度计算载荷工况 N
3.2 静强度结果分析
采用ANSYS对受电弓结构静强度进行计算,受电弓在各工况下的整体结构应力云图。见图12~图13基于第四强度理论计算主要部件的安全系数,结果表明:所有部件的安全系数均大于1,改性受电弓结构静强度满足要求;其中,闭口工况各部件的安全系数基本都小于开口工况,说明受电弓闭口运行时更为安全。
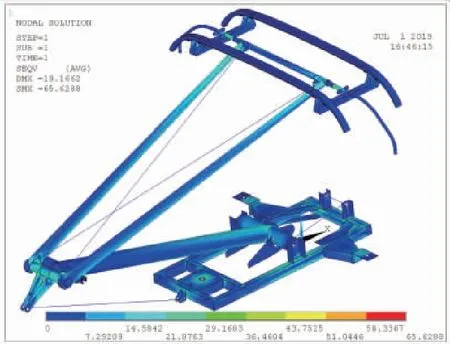
图12 开口工况应力云图
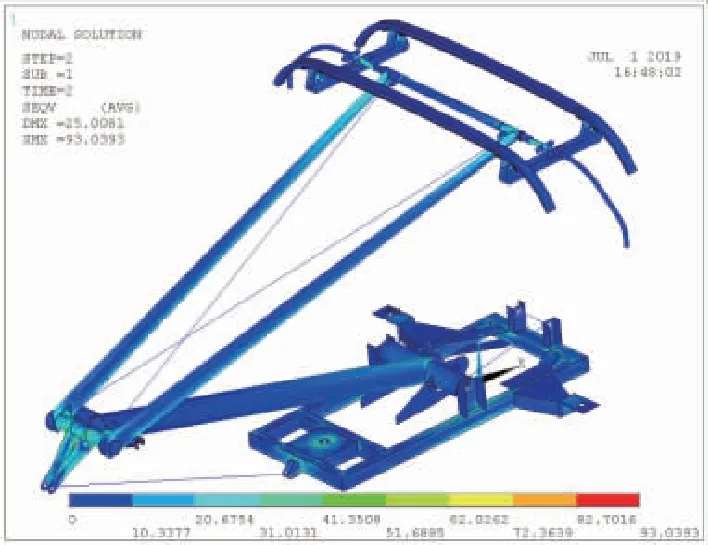
图13 闭口工况应力云图
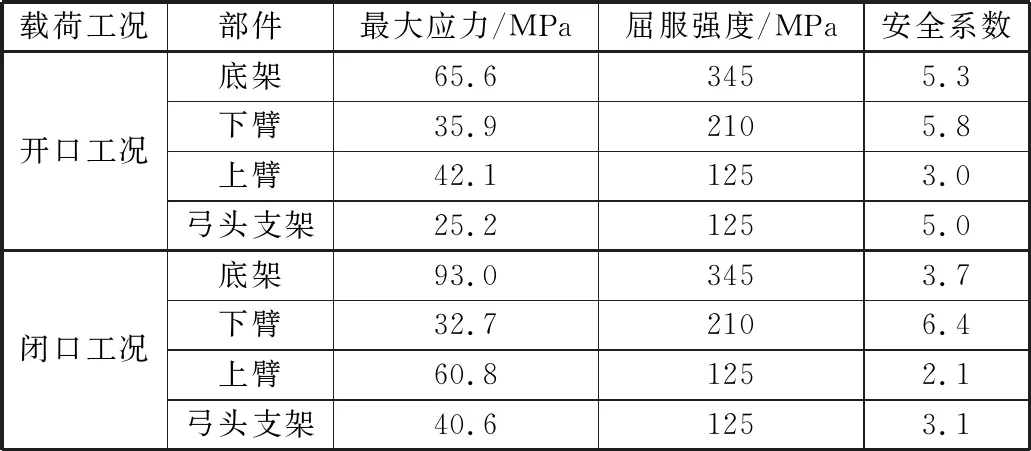
表4 静强度结果
3.3 焊缝疲劳强度分析
DSA200框架结构主要采用管材、型材和板材的焊接结构,而受电弓运行中处于多轴应力状态,需要将多轴应力转化为单轴应力,并结合相应的疲劳曲线来进行疲劳评价。采用将多轴应力转化为单轴应力的方法[6]和材料的Goodman疲劳曲线来评价结构的疲劳强度。
根据上述方法将焊缝节点的最大和最小应力在Goodman图上描点,得到受电弓上臂、下臂和底架焊缝的疲劳评价结果。如图14~图16所示,所有点均落在Goodman曲线的封闭区域内,上臂、下臂和底架所有焊缝节点的安全系数均大于1,说明该受电弓结构疲劳强度满足要求,且碳钢底架和不锈钢下臂的疲劳强度安全系数较大。
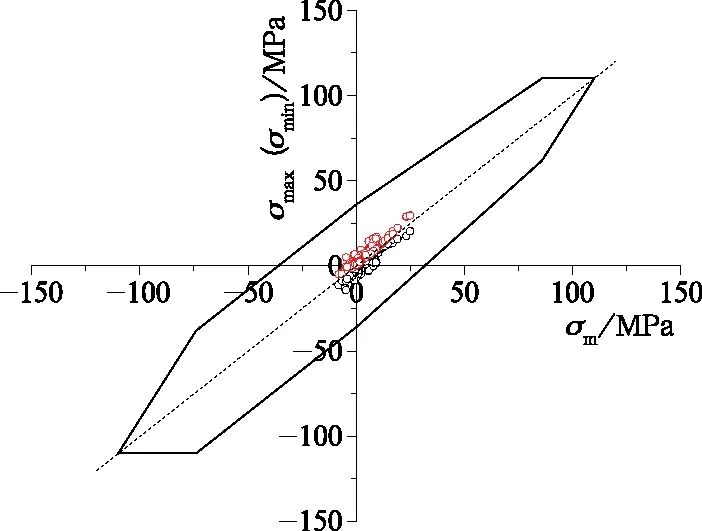
图14 上臂焊缝疲劳评价
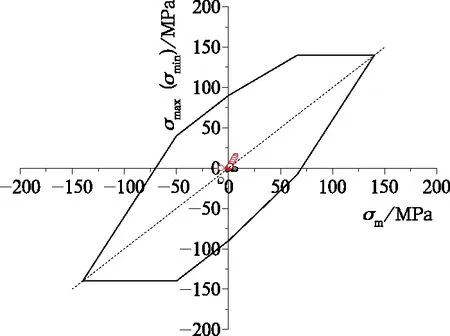
图15 下臂焊缝疲劳评价
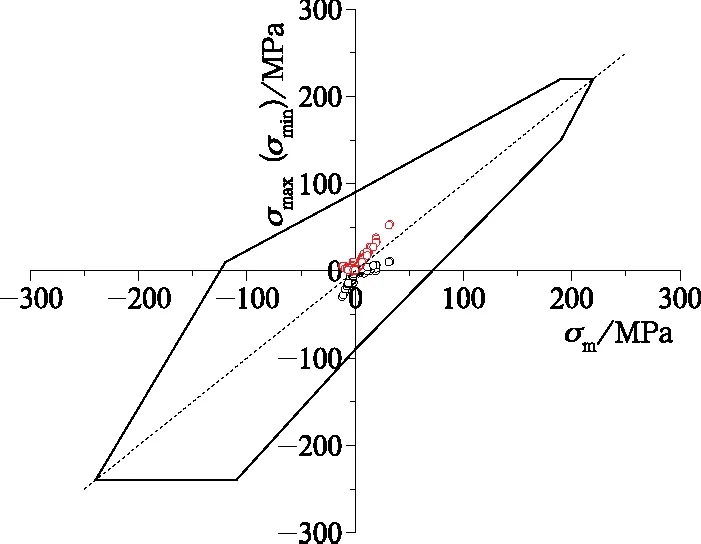
图16 底架焊缝疲劳评价
4 结 论
(1)通过的受电弓平面运动模型和等效参数的计算方法,完成了DSA200受电弓2质量模型等效参数的识别,该方法具有一定的通用性,可为后续弓网动态特性研究提供基础。
(2)受电弓框架归算质量和等效阻尼随受电弓座高度的变化而变化,两者取值范围分别为9.5~13.9 kg和12.0~27.5 N·m·s-1,且上臂弓头支撑和下臂对框架归算质量的贡献最大;而弓头等效刚度取决于铝支架和弓头支撑之间的垂向位移,其值在4 019~8 981 N·m-1之间。
(3)根据相关标准得到受电弓静强度载荷工况和疲劳载荷工况,在静载荷作用下,受电弓主要部件的最大应力小于材料屈服强度,安全系数的最小值为2.1,受电弓结构静强度满足要求。
(4)在疲劳载荷作用下,各焊缝节点应力结果均落在Goodman封闭曲线内,安全系数均大于1,DSA200受电弓疲劳强度满足要求,且上臂疲劳强度具有较大的安全裕量。
