肝肿瘤热消融治疗穿刺路径规划算法研究综述

张 睿， 周著黄， 吴薇薇， 高宏建， 吴水才

(1.北京工业大学生命科学与生物工程学院， 北京 100124； 2.首都医科大学生物医学工程学院， 北京 100069)

肝癌是世界第六大常见癌症，致死率高居第二位，严重影响人类的生存质量[1-3]. 治疗肝癌的首选方式是手术切除，然而肝肿瘤常见多中心发病，恶性程度高，易转移，且患者常伴有相关并发症(如肝硬化)，不足25%的肝癌患者能够接受手术切除. 同时，配型合适的肝源不足，使得肝移植手术受限. 因此肝癌局部消融治疗具有显著的临床意义[4-6].

过去十余年间，医学影像引导的肝癌局部消融术已确立成为继手术切除、肝移植后的第三大肝癌根治性措施[7]. 它是在医学影像(超声、CT、MRI等)引导下，将消融器械(消融针)经患者体表刺入病灶，利用能量或化学物质破坏病灶组织活性的微创疗法. 其大致分为能量消融和化学消融[6,8]. 能量消融包括热能消融与非热能消融，热能消融进一步细分为热消融(如射频消融、微波消融和激光消融)和冷冻消融；非热能消融则以不可逆电穿孔(irreversible electroporation，IRE)为典型. 热消融是将靶区组织加热(一般高于60 ℃)使其急性凝固性坏死. 冷冻消融则是将靶区组织冷却(一般低于-40 ℃)，破坏细胞代谢，形成冰晶和渗透休克[9]. IRE是用超短但极强的电场作用于细胞膜产生永久性致死的纳米孔，破坏靶区组织的稳态. 化学消融是通过注射液体化学物质(如乙醇、乙酸或氢氧化钠)破坏靶区组织，使细胞质脱水、细胞蛋白变性，形成微血管血栓，导致靶区组织凝血性坏死. 其中，肝肿瘤微波/射频消融治疗应用最广，已成为继手术切除、肝移植后的第三大肝癌根治性措施.

肝肿瘤局部消融治疗可分成术前、术中和术后3个阶段. 术前阶段或规划阶段包含2个关键任务：其一，明确患者腹腔内的解剖结构和病灶的相对位置. 该过程依赖医学影像处理，涉及肝外关键结构(如肋骨、脊椎、肺、胃、脾等)和肝内组织(如肝脏、肝血管、肝肿瘤等)的分割与重构. 相关算法自成体系，本课题组也做过初步研究[10-12]. 其二，遵循临床实际需求，规划消融针穿刺路径. 术中阶段或介入阶段是指临床医生遵循规划的穿刺路径，瞄准病灶，借由医学影像引导穿刺的过程. 穿刺过程中需要追踪并校正消融针的介入方向，直至消融针命中靶区. 术后阶段或评估阶段则是指借助医学影像分析实际的消融疗效. 其中，消融针穿刺路径规划是肝癌热消融治疗的关键，直接影响治疗效果.

目前，肝癌局部消融治疗以热能消融为主，其疗效与手术切除相比尚显不足，主要原因在于肿瘤的不完全消融会导致癌症的复发[13]. 此外，不合理的穿刺介入会引发血胸、气胸、感染或癌细胞扩散等术后并发症[14-15]. 产生这些不良治疗效果的主观因素在于：目前临床上广泛采纳的路径规划需凭借临床医生的经验，在患者采集的医学影像切片(二维序列)上手工设定[16]. 由于患者腹部的解剖信息并非直接可见，仅凭临床医生的主观经验规划穿刺路径十分困难. 而术前规划的不足又将导致术中消融的不可控，或伤及介入路径经过的器官和组织，或产生不理想消融效果. 不良疗效的客观原因则在于消融针在消融时生成的凝固区范围有限，且易受附近血管灌注与毛细血管微灌注导致的热沉降效应(heat sink effect)影响，使凝固区回缩，无法适形覆盖整个肿瘤[17-18]. 因此，研究准确有效的路径规划算法至关重要. 近年来，研究人员聚焦于借助计算机辅助规划系统，指导临床医生完成路径规划，以期提高肝癌局部消融术的疗效和安全性. 本文系统综述计算机辅助肝肿瘤微波/射频消融治疗穿刺路径规划算法.

1 临床多约束条件下的单针路径规划

手工路径规划对临床医生的专业素养有着苛刻的要求，尤其规划的路径与患者影像切片的夹角较大(穿刺路径贯穿多层影像切片序列)时，仅靠医生的经验进行路径规划耗时耗力. 因此，对于复杂病例，研究人员期望借助计算机辅助规划系统，为医生提供具有指导价值的进针位置和凝固区覆盖模型，在降低术前路径规划难度的同时提高路径规划质量. 随着图像处理与图像可视化技术的发展，学者将消融治疗的临床需求和目标量化成多个临床约束条件，以此作为计算机辅助规划系统的硬性要求. 首先介绍基于多种临床约束条件的单针路径规划.

1.1 临床约束条件

早期，Baegert等[19]总结了较为详尽的临床约束条件，并将其分成2类——强(严格)约束条件和弱(松弛)约束条件. 强约束条件是指在规划过程中必须遵守的准则，一旦违背则路径规划失败. 而弱约束条件是指在规划过程中需尽可能满足的要求，虽然违背弱约束条件并不直接导致路径规划失败，但所获得的穿刺路径并非最优. Schumann等[16]在后续的研究中补充了部分约束条件. 结合图1，对临床约束条件总结如下. 其中，黄色曲线示意皮肤；白色区域示意骨骼；灰色区域示意肝脏；蓝色区域示意肿瘤；红点t示意进针靶点；灰色虚线示意规划路径x；该路径分别交肿瘤边界、肝脏边界与皮肤表面于点T(x)、L(x)、S(x)；红色实线箭头示意路径x于肝脏边界交点L(x)处的肝包膜法向量为NL(x).

强约束条件：

1) 规划路径应规避腹部风险器官与组织. 这里的风险器官与组织包括穿刺可能波及到的肺、胃、脾、肾等脏器，肋骨、脊椎等骨骼及伴随的神经或神经丛；还包括若干贯穿肝脏内外的腹部脉管系统，记作R. 规避即要求规划路径不能刺穿甚至接触上述风险结构，即

(1)

式中r为风险结构R的任意一点；Nd为路径x的方向向量；l为算路径x的比例系数；lmax为该系数的最大值，等于消融针的针长；t+lNd为过点r作路径x垂线时所得的垂点坐标；Tr为距风险结构距离的阈值，通常这一参数设为大于0 mm的常量.

2) 规划路径深度应严格小于消融针长度. 即保证消融针能有效触及靶区并实施消融，即

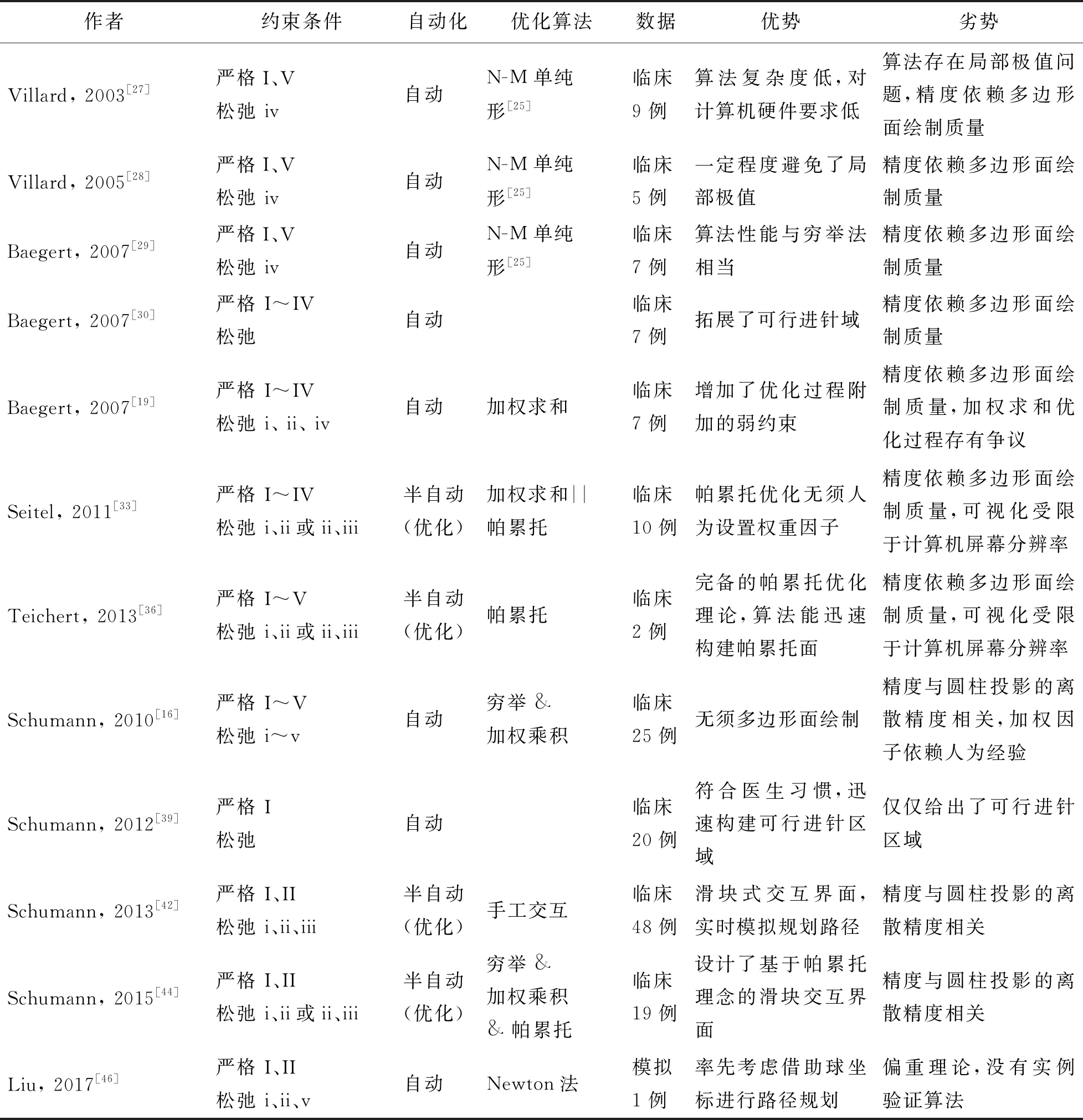
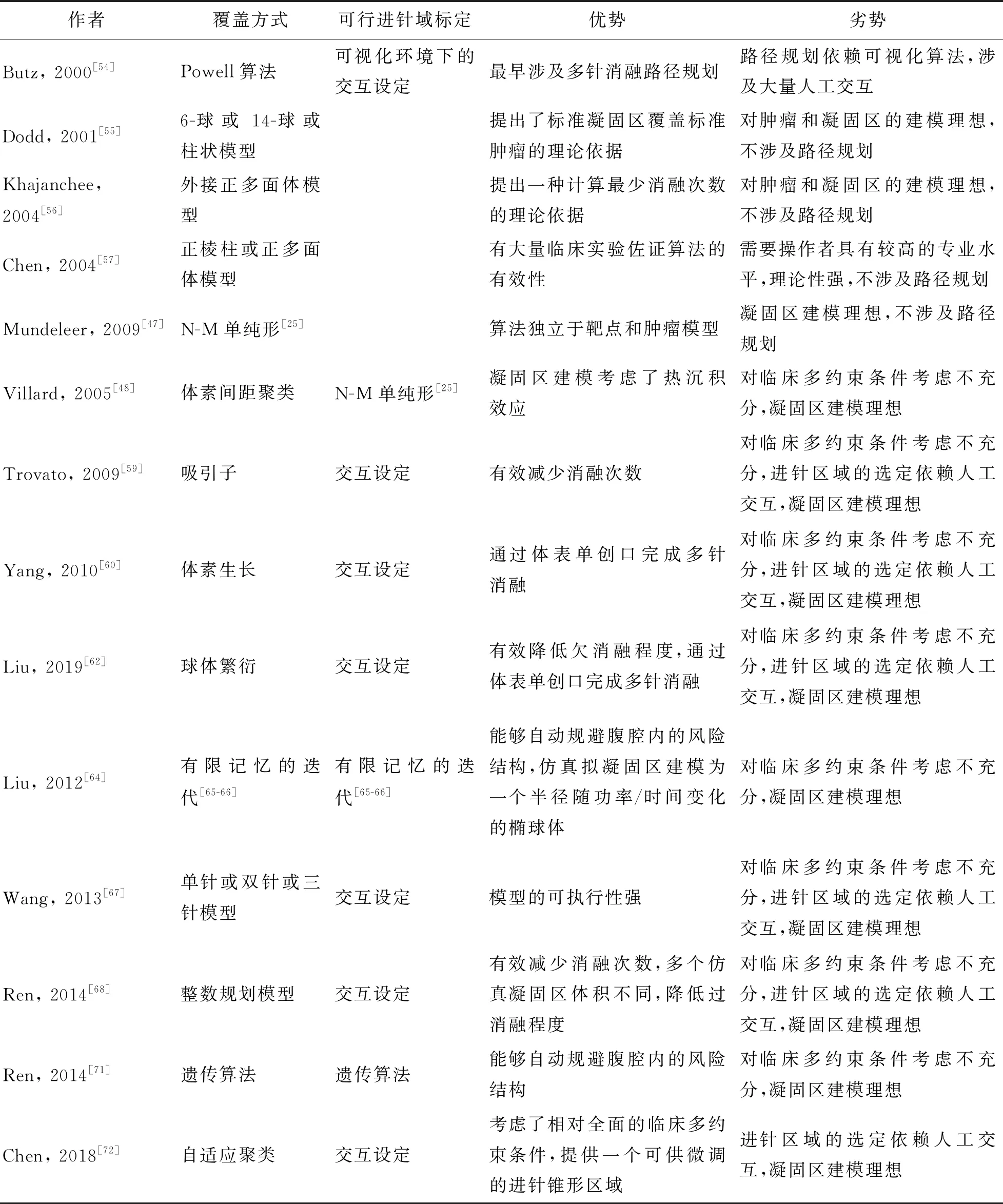
H2(x)=‖S(x)-t‖

(2)

式中Tl为穿刺深度阈值，通常设定为小于消融针长度的常量.

3) 规划路径应留有充足的止血距离. 临床要求消融针必需刺入肝脏实质一定深度(≥5 mm)，使得消融产生的凝固区不会超出肝脏边缘，同时留有足够的肝脏实质用以止血，即

H3(x)=‖L(x)-T(x)‖>Td

(3)

式中Td为经肝距离阈值，通常设为5 mm.

4) 规划路径与肝包膜表面夹角至少需要大于20°. 实际穿刺时，若消融针与肝包膜表面夹角过小，则可能发生滑针，甚至划伤肝脏，即

(4)

式中：Nl为肝包膜表面切向量；Ta为路径与肝包膜的夹角约束，通常设为20°.

5) 沿规划路径进行消融能够生成完全覆盖靶区的凝固区. 为防止肝肿瘤的不完全消融(以下统称欠消融)，通常会在肝肿瘤原有的体积上增大5～10 mm的消融区域，这段区域被称作安全边界. 路径规划时应保证消融针沿规划路径就位后产生的凝固区能完全覆盖包含安全边界的病灶区域，即

(5)

式中：Vt、Va分别为包含安全边界的肿瘤体积与预计消融的消融区体积；VtVa为两者重合的体积.

单针路径规划中强约束条件的平面示意如图2所示，其中蓝色区域代表肿瘤病灶，灰色区域代表肝脏，白色区域代表骨骼，粉色区域代表消融涉及的风险组织器官，红色扇形覆盖的区域代表不可进针区域，绿色体表轮廓代表可进针区域，深黄色区域代表止血距离不充足区域，2个绿色椭球示意凝固区恰能完全覆盖肿瘤的消融边界.

弱约束条件：

1) 规划路径应距腹部风险器官和组织尽可能远. 以免刺穿腹部脏器、血管，引发不必要的术中出血，或伤及神经导致术后长期神经性疼痛.

2) 规划路径的深度应尽可能浅. 在保证止血距离的前提下，越短的介入路径越能避免消融针与复杂风险结构接触的可能，同时降低癌细胞扩散的概率.

3) 规划路径与肝包膜的夹角尽可能大，贯穿层面尽可能少. 规划路径与肝包膜表面的夹角越大，则越有助于消融针刺穿肝脏，且产生更小的交互形变. 同时对患者实施腹部穿刺优先于背部穿刺. 另外，为了符合临床医生的操作习惯，规划路径与患者医学影像横截面的夹角越小越好.

4) 沿规划路径消融时尽可能减小对健康肝脏组织的损伤. 在保证完全覆盖靶区安全边界的前提下，尽可能减少对健康肝脏组织的破坏(以下统称过消融)，且尽可能减少所需的消融次数. 结合弱约束iv与强约束V即为“适形覆盖”.

5) 若由临床医生执行穿刺，还需考虑医生的操作习惯(如站位、姿势等).

综上，可以看出弱约束条件实际上和强约束条件存在一定程度的对应关系，更确切地说，弱约束条件是强约束条件的一种延伸.

1.2 多约束目标决策与数值优化

在明确临床约束条件后，研究的目标便转向求解多临床约束条件下的最优穿刺路径. 首先简述路径规划算法的数学模型. 路径规划可以抽象为决策与数值优化问题. 简言之，对于给定的变量x∈Rn，数值优化旨在使目标函数f(x)的取值达到全局最优(最小). 即通过预估对x初始化，再经过迭代估算和修正，最终使x的搜索止于全局最优解的过程[20]. 其数学表述为

subject tof(x)→mingj(x)≥0,j=1,2,…,m,hl(x)=0,l=1,2,…,e,f,gj,hl:Rn→R

(6)

式中m和e分别为相等约束和不等约束的数量. 式(6)描述的问题是数值优化的基础，称作单目标优化(single-objective optimization, SOO). 而实际的路径规划问题却涉及让多个决策目标函数fi(x)(临床约束条件)协同达到最优的过程，其中部分目标函数的优化过程甚至相互矛盾，这种问题则被称作多目标优化(multi-objective optimization, MOO)[21]，即

F(x):[f1(x),f2(x),…,fk(x)]T→min

(7)

式中：F(x)为k个目标函数fi(x)的矢量. 目标函数fi(x)在空间Rk中不存在优先级的区别，因此典型的MOO通常不存在单一的最优解，而是基于优化的预先定义，获取一系列相对较优的解集[22-23].

MOO问题的求解通常遵循标量化思想，将多目标矢量函数F(x)整合成一个标量目标函数F′(x)，使MOO退化成SOO，而后，就可以利用经典的求导或非求导策略对SOO问题求解. 求导策略常采用Newton算法，非求导策略范围广泛，在穿刺路径规划问题中常见Powell算法[24]、Nelder-Mead单纯形算法[25]、模拟退火算法[26]以及穷举算法等.

可以近似将路径规划过程归纳为：强约束条件是对路径x进行初始化，将x的取值空间进行二分类，满足强约束条件的取值空间被称作可行解空间，也就是可行进针区域，记作χ. 不满足强约束条件的取值空间则标记为不可行空间，如图3所示. 图3中黄色体表区域示意不可行进针区域，镂空体表区域示意可行进针区域. 而弱约束条件将被整合(标量化)，并借助经典的单目标优化求解策略，从可行进针区域χ中搜寻局部或全局优化解集χ*，如图4所示. 蓝色区域越深表示该区域进针越不理想，红色越深表示该区域进针效果越佳，最终求得临床多约束条件下的优化穿刺路径解.

1.3 单针路径规划算法

早先，Villard等[27]以理想椭球体仿真射频消融的凝固区，借助Nelder-Mead单纯形算法[25]搜索能够适形覆盖(强约束V、弱约束iv)肝肿瘤的穿刺路径. 该规划算法还涉及风险结构的规避(强约束I)，自定义一种源于图形渲染技术的拾取函数，函数返回搜索过程中消融针与风险结构的碰撞和深度信息. 算法通过9例临床数据进行测试，结果发现该算法严重依赖路径的初始搜索位置. 因此Villard等[28]提出了改进算法，借助规避风险结构(强约束I)初始化单纯形算法[25]的搜索空间. 算法对患者皮肤进行多边形面绘制，同时将肿瘤视作光源，风险结构视作不透光遮挡物. 若源于肿瘤射出的光线不被风险结构遮蔽，则光线能由构成患者皮肤的若干多边形承接. 所有光源完全覆盖的多边形即构成了初始化的穿刺路径搜索解空间. 该算法选择5例临床数据进行验证，结果显示对单纯形算法[25]进行初始化能够使穿刺路径远离风险结构环绕的间隙，并且降低对健康肝脏组织的误消融. 同一团队的Baegert等[29]借助穷举算法正面验证了改进算法[28]的性能，从对7例临床数据的路径规划效果来看，改进算法[28]在规避风险结构的前提下对肿瘤的适形覆盖能力与穷举法相当. 随后，Baegert等[30]扩展了规划算法需要考虑的强约束条件，在初始化可行进针区域时，附加了对穿刺路径深度、路径夹角和预留止血距离三方面(强约束II～IV)的约束. 研究人员还提出对重构成患者皮肤表面的多边形网格执行多尺度细化处理. 算法通过7例回顾性临床数据(共18个肿瘤)比对了实施多尺度细化策略前后的路径规划效果，结果表明多尺度细化策略拓展了可行进针区域，同时附加的运算时间也尚能接受. 同年，Baegert等[19]为规划算法补充考虑消融针的实际进针深度和消融针距风险结构的实际距离(弱约束i、ii)，构建了度量弱约束条件的评估函数，并采用加权和算法对弱约束条件加以整合. 算法由7例回顾性临床数据定性评估，在与专家手工规划的穿刺路径进行比对后发现，1例患者的计算机路径规划显著优于专家的手工规划，其余病例的规划效果相当.

针对MOO问题，加权求和算法尚存有一定的争议[31-32]，理想的加权结果并不等价于多个目标函数协同达到最优. 此外加权因子依赖于人为的主观因素，不利于算法自动化的实现. 为此，Seitel等在对针对伞形消融电极的路径规划研究中[33]引入了帕累托最优(Pareto optimality)理念[34-35]. 其规划算法在强约束条件(I～IV)构建可行进针区域内，由成对的弱约束条件(i&ii，ii&iii )构建帕累托面(Pareto frontier)，引导临床医生在帕累托面上筛选优化的穿刺路径. 算法通过10例消融失败(伴有并发症)的临床数据进行回顾性研究，与专家手工规划的穿刺路径进行比对，结果显示6例患者的手工规划路径是无效的(违反强约束条件)，4例患者的手工路径规划并不是最优选择，分别在一定程度上不合乎弱约束条件. 更详细的基于帕累托最优理念求解穿刺路径优化解的文献还可以参阅Teichert的工作[36]，论述了基于帕累托最优理念求解最优穿刺路径问题所涉及的概念和算法的原理，并给出了具体的数学证明. 同时作者还提出了一种自适应“超箱”算法(hyper-boxing algorithm)，能够快速部署基于成对弱约束条件的帕累托面.

至此介绍的路径规划算法均基于对患者的医学影像中相关脏器或组织进行多边形面绘制，以此重构出患者腹腔内的解剖信息. 这使得这类路径规划算法的准确性与运行效率严重依赖于面绘制流程中多边形的分辨率和多边形的重构质量，限制了算法的潜力.

Schumann等的研究团队为避免上述问题，提出了基于透视投影进行路径规划的研究思路. 在该团队的初步研究中，Schumann等[16]首先提出一种综合临床多约束条件(强约束I～V、弱约束i～v)的路径规划算法. 算法将临床约束条件分别量化，并采用穷举策略，以肿瘤靶点为中心对量化的约束条件进行圆柱投影(cylindrical projection)[37-38]，投影借2个偏转角将穿刺路径空间离散成若干路径列表，同时投影生成每个量化约束条件的约束图(constraint maps). 采用加权乘积的形式整合约束图，获得最终规划的穿刺路径结果. 考虑加权系数的合理性，还设计了针对不同约束条件的加权系数函数. 算法借助25例临床数据进行验证，邀请临床专家按1～6个等级对算法规划的穿刺路径评分(1-最好，6-最差)，结果显示84%的规划路径得分在2分以内(均值1.77). 通常，临床医生所接受的路径规划教学与实践均是在医学影像的二维切片上进行的，为了便于基于计算机辅助的路径规划算法融入这一工作流程，Schumann等[39]提出一种将不可行进针区域快速投影在患者影像切片序列上的可视化路径规划算法. 该算法仅针对规避风险结构这一强约束条件(强约束I)进行设计，在明确进针靶点和相关风险结构的重构场景后，基于立方体映射(cube map)概念，利用图形处理单元(graphics processing unit, GPU)加速体绘制得到风险结构映射图[40-41]，再将映射结果投影在患者采集的医学影像切片序列上. 在对20例肝脏射频消融病例的评估中，3名经验丰富的放射科医生表明该可视化算法对55%的病例有显著的辅助作用. 且2名专家指出算法显著降低了路径规划的耗时. 随后，Schumann等[42]又设计出一款基于滑块式交互界面的路径规划系统，界面能够容纳多个约束图所包含的全部进针路径以及每条路径对应的实际约束参数. 文献给出的示例界面上分布着4个约束滑块，对应路径的实际进针深度(mm)、路径与风险结构的实际距离(mm)，以及路径的水平偏转角与垂直偏转角(强约束I、II，弱约束i、ii，不完整的弱约束iii*). 滑块参数范围由对应的约束图限定. 临床医生拖动滑块设置对应的参数即可筛除不理想的进针路径. 同时，在界面中由滑块选定的穿刺路径会实时模拟显示在患者腹腔的三维重构场景中. 算法由2名没有临床穿刺背景的放射学专家和1名计算机人机交互领域的专家进行评估，采用用户体验问卷[43]统计评估结果，六方面的评分在1.750～2.410分. 为了设计出更具实用价值的计算机辅助规划系统，Schumann等[44]对先前的工作加以整合，并率先利用简化的温度场仿真凝固区替代理想的椭球体凝固区，对肝肿瘤适形覆盖的优化问题进行了更深入的研究. 同时，计算机辅助规划系统将穿刺路径的优选过程分成2步，首先利用多约束图筛选出“种子”路径，再结合Teichert工作[36]中的帕累托优化过程设计出新型的帕累托滑块，临床医生便能够交互式搜索出折中多临床约束条件的帕累托优化路径. 由19例临床数据对系统性能进行验证，与专家手工规划的穿刺路径相比，32%的计算机路径规划占优用户体验问卷[43]的6项评分在1.375～2.000. 2016年，同团队的Helck等[45]将该系统的第一阶段临床实验进行了公布.

Schumann团队提出的路径规划算法精度取决于圆柱投影. 因为投影过程中水平偏转角与垂直偏转角离散采样得到包含所有候选进针路径的列表，其离散程度将会影响路径规划的精度.

Liu等[46]采用球坐标形式，以肿瘤靶点为中心，固定消融针长度，研究消融针在不触及风险结构前提下的可达区域. 该规划算法专为具有3个自由度的手术机械臂而设计. 算法将消融针、风险结构和患者皮肤均进行离散点采样，以此构建消融场景，并借助进针深度与实际风险距离2项弱约束条件(弱约束i、ii)，利用Newton算法求取最优进针路径. 但该算法尚偏向理论研究，并未在临床数据上验证算法的可行性. 表1对临床多约束条件下的单针路径规划算法进行总结和对比.

2 多消融针协同消融的路径规划

第1节综述的路径规划算法对于单个肿瘤仅规划单条穿刺路径，即默认实施一次消融便能灭杀整个肿瘤. 事实上这种假设并不完备，研究表明，针对肝脏中径向长度小于2 cm的肿瘤，一次消融即可使之完全杀灭[47-48]. 一旦肿瘤径向长度大于3 cm，仅凭单次消融则无法将肿瘤彻底灭杀. 尤其当大肿瘤位于脏器深层时，目前临床有效消融的范围仅占病灶区域的29.0%～47.6%，因肿瘤欠消融导致癌症复发的概率高达60%[49-52]. 另有研究指出，多次消融会因凝固区的形成导致肿瘤的不透明度降低，从而增加术中消融效果的评估难度[52-53]. 同时，消融次数的增加势必加剧消融术的执行难度，提高并发症的产生概率，故而折中大肿瘤所需的消融次数就显得十分重要. 这是对肝肿瘤适形覆盖约束条件(强约束V、弱约束iv)的引申，既需要规划多条消融路径使消融凝固区完全覆盖大肿瘤，同时又需要尽可能减少消融次数，最小化过消融对健康肝脏组织的误伤. 因此将集中讨论这种大肿瘤的适形覆盖与规划算法.

表1 临床多约束条件下的单针路径规划算法比较Table 1 Comparison of single-needle trajectory planning algorithms under multiple clinical constraints

Butz等[54]最早开展大肿瘤路径规划算法的研究. 算法基于患者采集的MRI图像重构出患者腹腔的三维场景，场景中能交互式的置入一根仿真消融针，在避免与骨骼、血管碰撞的前提下模拟冷冻消融生成的凝固区域. 算法能够借助Powell算法给出适形覆盖肝肿瘤的优化进针位置. 这种半自动路径规划算法已经涉及到多消融针协同消融大肿瘤的模拟场景，但规划过程中需要大量的人工交互.

自动的大肿瘤适形覆盖算法最初建立在2个假设之上. 假设一：假设肿瘤的形态是标准的球体；假设二：假设消融形成的仿真凝固区是理想的球体或椭球体. Dodd等[55]和Khajanchee等[56]先后提出的覆盖模型可以视作大肿瘤适形覆盖算法的奠基. Dodd等[55]构建了标准的6球凝固区覆盖模型、14球凝固区覆盖模型和柱状凝固区覆盖模型. 并论证了3种仿真凝固区模型的有效覆盖范围. Khajanchee等[56]则提出大于或等于肿瘤直径的外接正多面体的面数即为适形覆盖大肿瘤所需的最少消融次数，论述了3～7 cm的球体仿真凝固区对3.00～6.23 cm的肿瘤进行适形覆盖所需的最小消融次数.

为了让消融规划更符合实际情形，研究人员放宽了对肿瘤形态的假设(假设一)，开始研究不规则肿瘤的适形覆盖问题. Chen等[57]采用正棱柱体和正多面体模型计算射频消融肝肿瘤所需的最少进针次数，并规划凝固区的最优重叠方式和消融针的最佳进针靶点. 其算法基础在于先对肿瘤中心进行仿真凝固区覆盖，再对肿瘤边缘或凸起进行补充消融. Mundeleer等[47]提出一种独立于进针靶点和肿瘤形态的大肿瘤覆盖规划算法，通过构造表示有效消融体积的代价函数，使用Nelder-Mead单纯形算法[25]获得消融针的最佳进针靶点. 然而上述算法[47,55-57]仅仅考虑了大肿瘤的适形覆盖，却没有与路径规划问题相结合. 接下来介绍的研究工作则对这一不足进行了扩展研究.

Villard等[48]研发的肝肿瘤射频消融规划工具包“RF- Sim”，包含对大肿瘤进行多针消融的路径规划. 规划算法以初始化的进针靶点作为聚类中心，借助距离变换(distance transform)[58]将大肿瘤按体素间距聚类成多个病灶亚区. 再利用单纯形优化算法[25]求取每个病灶亚区的进针靶点和进针路径. Trovato等[59]提出的大肿瘤覆盖规划算法兼顾病灶组织的有效消融与肝脏组织的误消融. 算法首先在病灶区域的包围盒上排布足够多覆盖肿瘤的球体仿真凝固区，再借助定位在靶区中心与仿真凝固区球心的吸引算子(attractors)吸引仿真凝固区向病灶中心靠拢，并迭代更新仿真凝固区的覆盖情况，删除冗余消融，最终在患者体表反馈消融针的进针位置. Yang等[60]提出的大肿瘤适形覆盖算法基于“体素生长”理念，依据肿瘤的轮廓自适应生成多个进针靶点. 同时为减少消融次数并减小肝组织误伤，“生长区域”需最佳拟合病灶的几何形状. 算法将肿瘤体素划分成多个连续的体素立方体，每个立方体按肿瘤轮廓逐层“生长”，其生长中心即对应的消融靶点，其外接球体即对应的仿真凝固区. 同一团队的后续工作中，Duan等[61]将该算法整合到手术机器人系统中，通过患者皮层的单一切口实现多个射频消融针的穿刺介入. 并通过大量基于离体猪肝的实验证实了该算法的可行性. Liu等[62]则延续这2项工作[60-61]，设计出基于皮肤单创口的多针协同消融系统，为有效覆盖不规则大肿瘤，作者提出一种名为“球体繁衍”算法，该算法基于六方密堆积理论[63]，基于有效消融与过消融程度自动生成一系列覆盖肿瘤的球型仿真凝固区. Liu等[64]提出的微波消融规划系统能根据选定的进针位置和肝肿瘤体积自动计算出所需的最小消融次数. 算法的仿真拟凝固区建模为一个半径随功率/时间变化的椭球体，其代价函数反映了肿瘤靶区的欠消融程度与肝脏组织的过消融程度，同时也对涉及风险结构的路径进行附加惩罚. 算法优化过程则选用有限记忆的迭代算法[65-66]实施. Wang等[67]从理论层面上由几何优化模型改进不规则肝肿瘤的消融规划，作者指出对同一肿瘤规划出3次以上的消融便几乎不具备实施的可行性. 因此作者从二维层面的内接三角形法和细分法对仿真凝固区的适形覆盖问题进行建模，最终将所有肿瘤的适形覆盖问题归结为单针消融、双针消融、三针消融和无法消融4类. 算法在确定治疗所需的最大消融次数后优化消融针的介入路径. Ren等[68]在早先工作[69-70]的基础上，提出一种求解整数规划模型的路径规划策略. 算法的初始化进针点由临床医生标定，算法包含最少(径向)轨迹整数规划和最小消融整数规划两部分，分别获得覆盖肿瘤所需的最少径向轨迹以及沿径向轨迹对应的最少消融次数. 其算法能够生成多个可行方案，需由临床医生进行参数评估和可视化比对并做出抉择. 同年，Ren等[71]还提出了一种肝肿瘤消融规划系统，利用遗传算法对最优覆盖问题进行了启发式的求解. Chen等[72]以符合临床约束条件的可行进针区域为前提，通过自定义的聚类算法和覆盖迭代优化算法完成了基于多约束条件下的大肿瘤适形覆盖规划. 聚类算法将病灶初始化成几个体积相当的病灶亚区，且每个亚区的形态均近似于仿真凝固区. 覆盖优化算法则使每个亚区的仿真凝固区最小化，同时迭代计算出所需的最小消融次数. 为了避免规划路径与风险结构碰撞，算法附带了可供微调的可视化椎体进针区域. 表2总结并对比了多针消融路径规划算法.

表2 多针消融路径规划算法比较Table 2 The comparison of multi-needle ablation path planning

3 路径规划中的其他关键问题

3.1 消融凝固区仿真

为进一步放宽路径规划算法中对仿真凝固区标准模型的假设(假设二)，使路径规划过程中能够使用更趋近真实的消融凝固区，则需借助凝固区温度场仿真相关研究.

现有的凝固区仿真研究普遍认可通过生物热传导方程(bio-heat transfer equation)对热消融温度场进行有限元仿真. 但肝肿瘤消融的环境复杂，涉及肝脏组织的诸多特性(包括电导率、导热系数、热容量、组织密度、组织温度、含水量和蛋白质状态等)，因此复杂的仿真模型常受限于计算机求解效率，以至于部分研究仅具有较强的学术价值[73]. 研究人员或倾向模型的简化[48]，或借助GPU对仿真运算进行加速[74-75].

多数生物热仿真都基于Pennes生物热方程[76]，其热传导项源自于傅里叶经典导热定律，考虑了代谢产热和血液灌注传热2项因素，是计算生物传热温度场最简洁的模型. 但是，傅里叶导热定律隐含以下假设：热量在介质中的传播速度为无穷大，这与热消融过程中的热传导作用不符. 随着研究的深入，基于非傅里叶导热定律的Hyperbolic方程被提出[77-78]，其主要思想是热通量与生物组织中温度梯度的传导存在常量延迟时间. 早年，在角膜和心律失常射频消融治疗中，Hyperbolic方程已被用于三维温度场分布的计算[79]. 下面以肝肿瘤热消融术为背景，介绍微波消融、射频消融和冷冻消融中有关凝固区仿真的研究进展.

微波消融和射频消融温度场仿真一般基于Pennes生物热方程，建立消融的有限元模型. 由于肿瘤的个体差异性很大，需要建立精确的三维温度场仿真来确定微波热疗手术中的最佳加热参数[80]. 对于微波消融温度场仿真精度的研究，目前国内外的研究主要集中在求解比吸收率(special absorption rat, SAR)的分布的精度[81-82]、肝组织热物性参数的设定[81]、血液灌注以及汽化作用的影响等方面[83]. 类似的，为建立射频消融有限元模型，在仿真软件中通过电- 热场耦合分析预测热损伤区域的温度变化，也不乏射频消融温度场仿真的研究[84-88].

近年来有关冷冻消融的研究相对较少，中科院理化所的相关团队利用纳米颗粒提出一种新的纳米冷冻消融术[89]，并对引入纳米粒子的冷冻凝固区进行了理论性的三维仿真[90-91]，并充分考虑了大血管血流的流动性导致的热传导现象，由大量动物的载体实验证明将导热系数较高的纳米颗粒注入冷冻靶区能够显著降低血流造成的热沉降效应，缩短冷冻消融时间，扩大有效的冷冻消融范围.

但目前尚缺乏将仿真凝固区与肝肿瘤消融路径规划算法结合的相关研究，仅Schumann等[45]的研究中采用同课题组的数值模拟模型[75]将仿真凝固区的覆盖作为路径规划的强约束条件，用于穿刺路径的初始化.

3.2 刚性路径规划与弹性路径规划

肝癌局部消融路径规划是将规划的穿刺路径抽象做体表进针点(集)与病灶靶点(集)间的对应线段，借助“刚性”这一概念对这种不涉及形变的线段路径命名为“刚性路径”，相关的规划算法则被命名为“刚性路径规划”. 但在实际的穿刺过程中，刚性路径规划并不足以满足临床需求，因为穿刺过程势必面临2类形变. 形变一：消融针在刺穿过程中因针尖对体表或脏器表面产生的压力，以及消融针在刺入人体组织时产生的摩擦力，会迫使消融针和人体组织发生形变. 形变二：患者的呼吸作用致使肝脏产生类似周期性的位移和形变，改变了肝肿瘤与体表的相对位置. 形变致使所需的穿刺路径可能是不规则的曲线段，将之命名为“弹性路径”，对应的规划算法命名为“弹性路径规划”. 由于2类形变的复杂程度，弹性路径规划在近年的学术研究中一直是悬而未决的难题.

针对形变一进行经皮介入路径规划算法的研究并不多见，Hamzé等[92]提出了一种在组织运动且针头弯曲情况下的肝癌消融路径规划模型. Tan等[93]则基于马尔科夫决策，对柔性消融针的穿刺路径进行规划. 详尽的针- 组织交互形变建模可参见近期发表的综述论文[94]，但相关模型鲜见应用于肝癌局部消融术的路径规划中. 同时，没有查阅到有关肝癌局部消融术中路径规划过程涉及呼吸运动形变补偿的相关文献，仅有研究专注于呼吸形变模型的构建. 常见的建模方式包括：1) 仅基于医学影像处理，预估病灶的位置信息[95-98]； 2) 借助标记传感器反馈的信号，追踪病灶的周期性位移[99-101].

4 讨论与总结

本文综述了经皮介入肝癌局部消融治疗穿刺路径规划算法，相关的规划算法也适用于肝脏的活检等临床检测或规划其他脏器的穿刺治疗.

综合来看，刚性穿刺路径规划算法的发展趋势在于结合日渐成熟的可视化算法，对消融场景进行准确且有效的三维重构，在完备的临床多约束条件下快速获取满足强约束条件的可行进针区域，并结合合理的数值优化算法对多约束优化问题快速求解.

而对于弹性路径规划，研究的趋势在于有效建立肝脏组织的动态图谱，或引入带有运动信息医学影像序列，完成多模态医学影像的配准；或依赖单模态医学影像序列完成包含组织解剖结构和运动规律特性的四维运动图谱的构建.

此外，路径规划问题甚至需要跳出单纯的图像处理领域，结合新的学科，如借助材料领域的纳米粒子，规划并实行疗效更佳的肝肿瘤局部消融术.

遗憾的是，虽然有关路径规划算法的研究已经取得了一定的成就，但依然鲜见于临床的实际应用中. 说明目前的学术研究距临床应用还存在差距，还有许多实际问题没有得到有效的解决. 现有的研究中，基本默认消融针的进针靶点在小肿瘤的质心或大肿瘤的亚区质心. 但临床上，消融针通常会刺穿肿瘤执行消融，而目前没有相关研究对消融针的实际靶心位置进行明确的数学建模. 此外，由于消融针贯穿肿瘤，那么贯穿部分的消融针又涉及是否触碰风险结构等关键约束. 在针对大肿瘤的路径规划中，默认多次消融效果相当于单针消融效果的多次叠加，但实际上多针协同消融的凝固区生成会更加复杂. 更难以有效且准确地快速建模. 此外，凝固区的有限元仿真、呼吸反馈模型和针- 组织交互形变模型的生成效率，尚且难以满足实际的临床需求，模型精度也存在局限，更难以将多级数学模型有效的统一在路径规划问题中. 因此穿刺路径规划算法还有许多难题等待攻克.