基于TSP 模型的游览路线设计研究——以徐州潘安湖风景区为例

肖人峰，陈 瑞，李静雯，苏小珂，张 斌

（成都信息工程大学 通信工程学院，四川 成都610225）

1 引言

本研究选取潘安湖景区的部分景点，完成徐州潘安湖风景区游览路线设计问题[1]。假设游客在景区停留的时间由景点之间的步行时间、景点游览时间（即在景点内游玩的时间）、在景区外的等待时间三部分组成，其他时间忽略不计。

2 模型建立

给每个景点编号：0 为景石，1 为游客服务中心，2 为阳光草坪，3 为森林小剧场，4 为儿童科普体验区，5 为儿童戏水场，6 为湿地博物馆，7 为湿地商业街。

已知dij表示景点i和景点j之间的距离，则这8 个地点之间就存在着这样一个距离矩阵D。它的特点为：D是一个8×8 的方阵，其对角线元素全部为0，其他元素是以对角线元素为对称轴对称分布的。

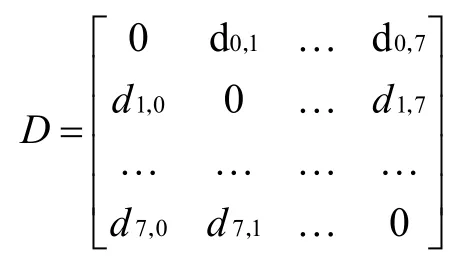
对于旅游路线优化的问题，可以抽象地描述为从景石出发，遍访7 个景点求总距离最短的闭合路径。于是这个旅游路线问题的有效解为这7 个元素的一个循环排列C={C0，C1，…，C7}，（Ci∈[0，7]，当i≠j时Ci≠Cj）。

求旅游路线问题的最优解，就是寻找一个C，使得下列目标函数值最小其中dCiCj表示景点Ci和景点Cj之间的距离。

游客旅游时未达到尽量缩短路程的目的，凭经验一般会这样确定路线：根据各景点的分布情况，将其划分在不同的旅游区。游玩时先确定不同旅游区的先后顺序，再确定同一旅游区内各景点顺序。此思想可看出，相距较近的两景点形成直接通路的可能性较大，相距较远的两景点由于可能分属于不同的区，形成直接通路的可能性较小，而形成间接通路的可能性较大。

各景点根据“远近亲疏”的关系，按远近分别划分在不同的旅游区。应用同样的思想，同一旅游区内各景点根据距离远近不同，又可划分成次小区，次小区内又可继续划分，直到划分的最后区域只包含单个景点元素。

上述是一种递归的思想，与树结构的递归定义十分类似，所以可以把这种层次关系用树的分支结构表示的层次关系描述出来。本文用树中结构最筒单的二叉树描述这种关系。根据上述确定最短路径的原则和分析思路，建立一棵二叉树把16 这个元素的相互距离关系描绘出来。

建立二叉树的基本原则是：距离较近的景点应位于二叉树较近的分支上，距离相对最近两个景点是“兄弟”关系，二者结合成一“景点组合”作为他们的“双亲”结点。这个“景点组合”作为一个整体元素再加人到下一轮的距离比较中。例如：在上述8 个元素（包括7 个景点和序号为0 的景石）中，景点6 与景点7 距离最短，首先把它们结合起来，并赋予编号8，可称之为景点组合8。用二叉树表示景点6和景点7 以及景点组合8 的关系为以6、7 作为孩子结点（这里同时也是叶子结点），8 作为结点6、7 的“双亲”。而景点组合8 与其他某景点k之间的距离用公式计算：

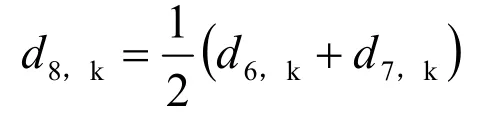
这里d8，k为景点组合8 与景点k的距离，d6，k为景点6与景点k的距离，d7，k为景点7 与景点k的距离。这时把景点6 和景点7 从原问题中消去，取而代之的是它们的元素组合8。因此，这个景点的旅游路线问题被改变为7 个景点来处理。类似的，可确定7 个景点中剩下相距最短的2 个景点，推算可知为景点1 和景点8。这2 个景点也被组合起来，编号为9。以此类推，不断将各元素组合，这样得到的最后一个元素组合15 就能把所有景点包括进去。

使用下面公式计算距离时，将a、b、c、k可看作为一个整体。

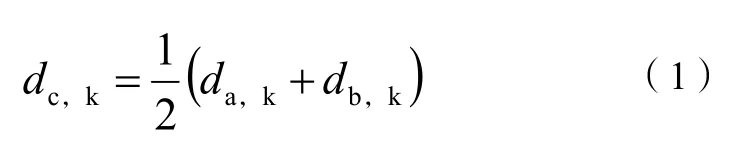
式（1）是a，b的组合，而a，b，k可以是某一单点元素（当编号在[0，7]内时），也可以是一个元素组合（当编号在[7，14]内时）。若a、b、k之中还存在元素组合，假设b就是个组合，则将db，k继续按照式（1）展开，直到最终导出叶子结点间的距离关系，将距离dc，k计算出来。

3 模型求解

遍历二叉树并建立最短闭合回路主要包括三个环节：把当前分支结点i从当前闭合路径中删除；找到当前结点i的右孩子结点1，按照使当前闭合路径为最小的原则，将其插入到当前闭合路径；找到当前结点i的左孩子结点h，按照使当前闭合路径为最小的原则，将其插入到当前闭合路径。

采用二叉树方法描述旅游路线优化问题的最终具体路径，结果如表1 所示。

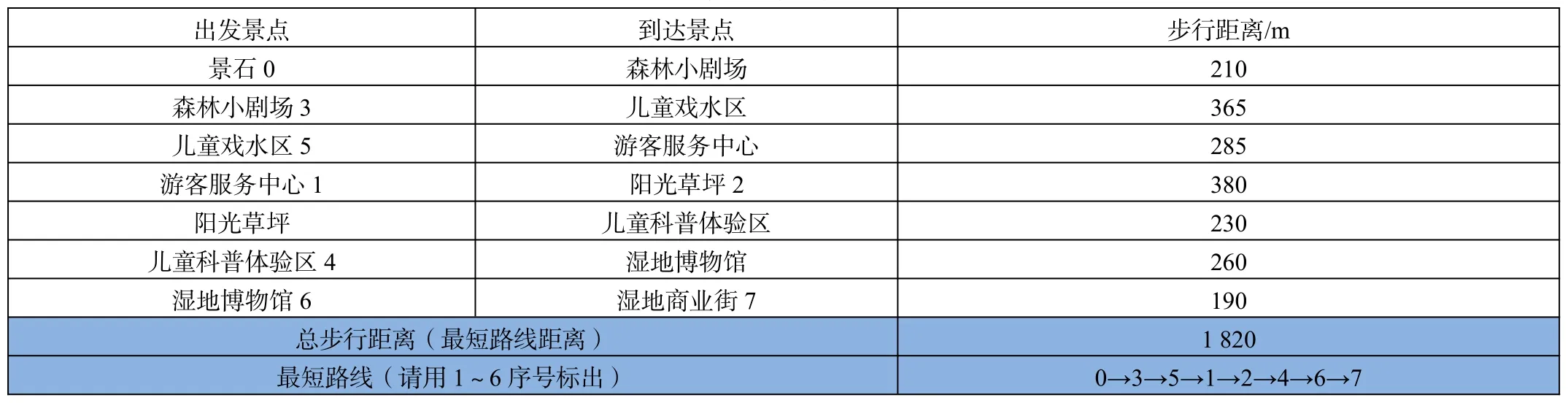
表1 结果表格