爆炸冲击下重力坝不确定性动态响应研究

蒋云怒，胡安奎，刘伯相，杨泽江

(1.西华大学流体及动力机械教育部重点实验室，四川 成都 610039；2.四川水利职业技术学院，四川 成都 611231；3.西华大学能源与动力工程学院，四川 成都 610039)

研究重力坝在爆炸荷载作用下的破坏效应和抗爆性能，对大坝的安全评价和可靠性分析有重要意义[1]。国外学者中，库尔[2]从水下爆炸物理现象开始，对水下爆炸的流体动力学理论、炸药爆轰与冲击波的形成及传播、水下爆炸实验技术、气泡运动及二次压力波、水下爆炸对平板的作用等进行了详细的阐述和讨论，为水下爆炸理论奠定了基础。Linsbauer[3]通过建立库水—坝体耦合模型，对库底爆炸冲击荷载作用下的混凝土重力坝的动力响应、稳定性及破坏机理进行了研究。国内学者中，李鸿波等[4]以连续损伤力学为基础，将有效应力和损伤应变能释放率的概念引入岩石类介质的脆性动力损伤演化模型中，分析了大坝在爆炸冲击荷载作用下动力响应过程。张雪东等[5]采用离心模拟爆破系统，初步研究了不同水深，与坝面不同距离情况下的雷管爆破对大坝的影响。

通过以上研究现状可以看出，爆炸的研究已经涵盖了很多方面，但是大多采用的都是单一的经验公式和数据，将爆炸荷载作为确定值处理，显然这与事实不符，爆炸受诸多因素影响，所以爆炸荷载应该是一个不确定的值，如果在实际工程中仅仅将爆炸荷载考虑成确定的值，一旦事故发生，实际荷载大于所采用的确定值，坝体就会出现不可预测的毁伤，而这样的情况是很有可能发生的，因此本文研究爆炸荷载的不确定性，给出爆炸荷载的分布规律，为坝体防护提供限度，从而达到既不至于浪费材料又能抗爆的目的。

1 爆炸荷载统计模型

1.1 空中爆炸荷载参数的不确定性分析

分析空中爆炸荷载的过程中，由于各种不确定性的因素影响(如爆炸波传播过程中的反射、衍射等；计算方法和建立模型的差异等)都会使得相同比例距离下爆炸荷载的测值有所差异。

由于空中爆炸冲击波峰值衰减较快，大气压强不可忽略。因此空中爆炸一般采用峰值超压(Peak overpressure)表示各点的冲击波压力。

Brode[6]在1959年提出入射超压峰值Ps0与比例距离Z间的关系(超压峰值单位为MPa)

(1)

Henrych等[7]在1979年进一步给出了超压峰值Ps0的经验公式(超压峰值的单位为MPa)

(2)

由以上所列举的不同经验公式可以看出，爆炸荷载的正反射超压峰值Ps0具有很大的波动性，不同学者得到的公式也具有很明显的差异，为了建立全面的爆炸荷载超压峰值的统计模型，除了上述的相应公式以外，还收集了一些爆炸试验的试验数据，通过以上爆炸荷载超压峰值的统计结果不难看出，爆炸荷载入射超压峰值具有非常明显的不确定性，即使是在同样的比例距离下，实测得到的入射超压峰值还是有很大的差异，因此有必要作进一步的研究。

1.2 空中爆炸荷载参数的统计模型

1.2.1空中爆炸荷载参数的统计

为了分析爆炸荷载入射超压峰值Ps0的统计特性，对于不同专家学者总结的有关超压峰值的经验公式与试验实测数值在不同比例距离下的数据进行了分析(见图1)，进一步说明了爆炸荷载的波动性。从图1可以看出，比例距离越小，这种波动性就越明显，而比例距离越小，对坝体造成的破坏越大，造成的损失也就越大，因此有必要更进一步研究爆炸荷载超压峰值的规律。

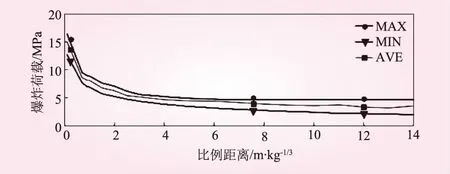
图1 不同比例距离下超压峰值的范围

1.2.2空中爆炸荷载参数的曲线拟合

利用MATLAB对不同比例距离下超压峰值的平均值、标准差和变异系数进行曲线拟合，得到超压峰值数值与比例距离的数值在对数坐标系下的曲线，如图2所示。

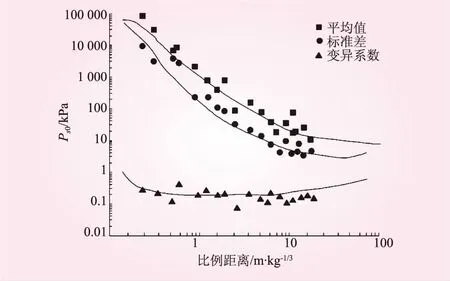
图2 不同比例距离下超压峰值的平均值、标准差和变异系数的分布

2 材料本构模型

2.1 混凝土本构模型

在爆炸冲击荷载作用下，混凝土材料有高应变率和非常复杂的动态响应，其失效强度随平均压应力的增大而增长，抗拉强度显著提高，对应力状态的影响明显。Riedel-Hiermaier-Thoma(RHT)是基于HJC本构模型[8]发展而来的，由Riedel等提出。RHT模型[9]能够很好地描述混凝土建筑物在爆炸冲击波作用下的大变形、高应变率以及高压作用下的毁伤过程。

2.2 坝基岩体本构模型

炸药在混凝土重力坝附近爆炸时，基岩的变形较大，基岩应变率效应明显。因此，在爆炸荷载作用下的岩体损伤本构模型采用考虑应变率效应的塑性硬化模型，该模型材料属于各向同性应变率相关塑性材料中的塑性随动材料，岩体屈服应力[10]与应变率的关系如下

(7)

(8)

3 状态方程

3.1 炮轰产物状态方程

炸药材料采用JWL(Jones，Wilkins和Lee，JWL)状态方程[12]描述爆轰压力P和每单位体积内能E及相对体积v的关系，即

(9)

式中，v为爆轰产物体积和炸药初始体积之比；E为炸药初始内能；C1、C2、R1、R2和ω为材料特征参数，C1=3.738×1011Pa，C2=3.747×1011Pa，R1=4.15，R2=0.9，ω=0.35。

3.2 空气状态方程

空气的状态方程通过Mat-Null材料模型[13]和线性多项式状态方程来描述，即

P=C0+C1μ+C2μ2C3μ3+(C4+C5μ+C6μ2)E

(10)

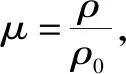
4 空中爆炸模型的建立

4.1 AUTODYN拉格朗日和欧拉耦合算法

本文所建立的数值模型，使用AUTODYN显式动力学软件，AUTODYN[14]提供多种求解器，本文使用的是拉格朗日(Lagrange)求解器和欧拉(Euler)求解器[15]，拉格朗日(Lagrange)求解器主要用于模拟结构实体单元、壳单元和梁单元等的响应，而欧拉(Euler)求解器则用于模拟气体和液体的流动，如爆轰波[16]的形成、传播，解决流固耦合等问题。

欧拉模型可以模拟流体扩散[17]及混合现象，欧拉方法与拉格朗日方法有所不同，欧拉模型的网格是固定不动的，所以只要是在计算过程中材料有可能到达的区域，都需要划分单元网格。欧拉模型随着材料在固定的单元网格中运动，在运动的过程中，模型的界面不断重新定义。

拉格朗日计算循环是从设置的初始条件和边界条件开始，利用动量方程求出拉格朗日节点的加速度、速度及节点位置等。有了这些量和新的单元体积后，就可以计算出相应的应变率。然后在材料模型和能量方程的基础上，求出单元应力和能量，进入下一循环节点力的计算。AUTODYN采用的是侵蚀算法，这种算法可以将大变形网格自动消除掉，可有效地避免因网格扭曲造成的计算精度下降、计算步长变小等问题，更避免了由于网格严重扭曲导致的计算提前结束的问题。

4.2 空中爆炸模型的建立

本文以国内某混凝土重力坝[18]右岸非溢流坝段为研究对象，该坝段高105.0 m，坝顶宽16.0 m，坝底宽75.0 m。坝体三维模型见图3，模型包括混凝土重力坝、地基、空气和TNT炸药4种物质的耦合，共有202 500个单元，大坝和地基采用拉格朗日网格建模，空气和TNT炸药采用欧拉网格建模，空气与大坝和地基之间采用拉格朗日-欧拉流固耦合算法。

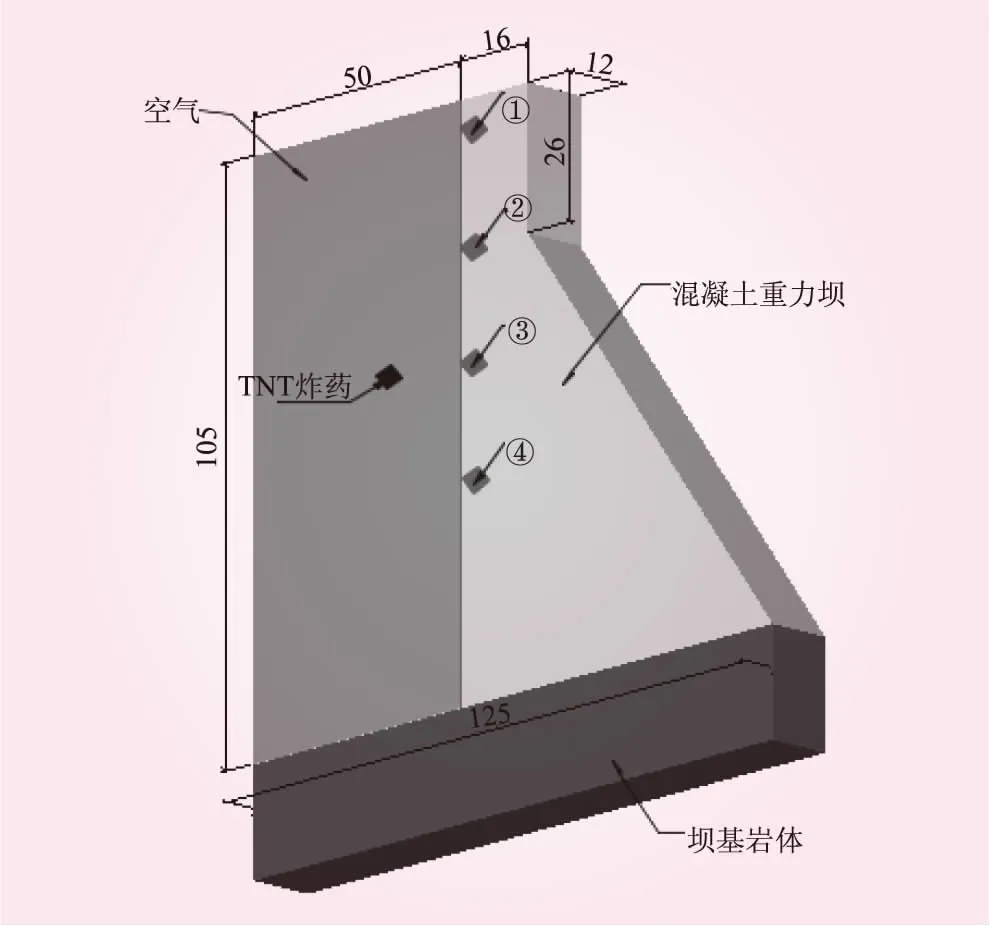
图3 坝体三维模型(单位：m)

本文建立数值模型是为了模拟混凝土重力坝在不同的爆炸荷载和比例距离下的动态响应，采用最大爆炸荷载、平均爆炸荷载以及最小爆炸荷载来对混凝土重力坝进行作用，从而得到重力坝动态响应的分布规律及范围，考虑的比例距离共12组，分别为0.1、0.7、0.9、1、1.5、2、4、6、8、10、12、14 m/kg1/3。

为研究混凝土重力坝在空中爆炸[19]荷载作用下的动态响应特性，取坝段上游面的4个点作为监测对象，对其在空中爆炸荷载冲击过程中的应力、位移、速度以及加速度进行监测，从而得出混凝土重力坝在空中爆炸冲击荷载作用下的动态响应规律。4个监测点分别位于坝顶处、下游坝坡对应上游面处、炸药等高处(60 m坝高处)以及30 m坝高处，相应测点编号为1、2、3、4，监测点布置示意见图4。

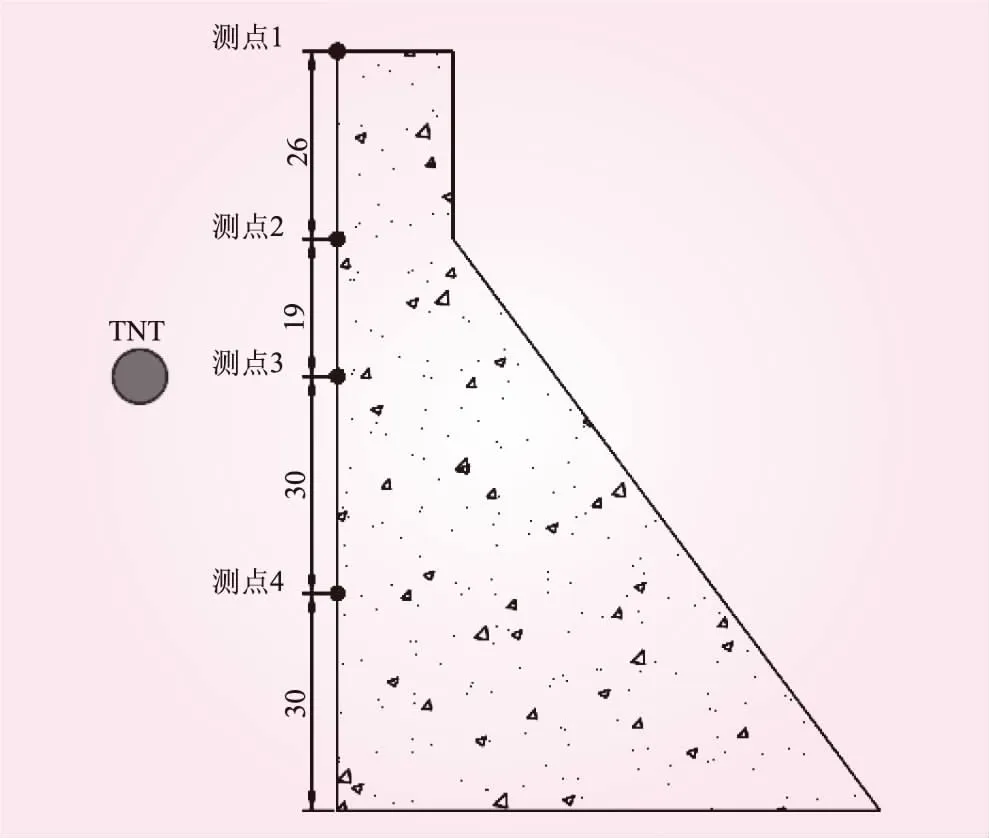
图4 坝体剖面及监测点的布设位置(单位：m)

5 混凝土重力坝的动态响应

5.1 不同测点的动态响应分析

对同一比例距离下的不同测点的动态响应进行分析，得到重力坝不同位置处的测点在相同比例距离下的响应规律。

当比例距离为0.7 m/kg1/3时，各测点的动态响应如表1所示。

在其余各比例距离下的4个测点动态响应的规律和特点与上述结果无明显本质差异，仅以为0.7 m/kg1/3为例，其余在此不再赘述。根据所得数据不难发现：无论在何种输入荷载下，测点3的动态响应在4个测点中都是最大的，测点2的动态响应次之，然后是测点1，最小的是测点4(这一规律在位移这一响应中并不成立，由于爆炸初始时刻位移非常小，而且易受结构影响，例如测点1布设在坝顶，坝体一旦受到爆炸荷载的作用就会不可避免地产生一定的震动，而坝顶的震动幅度显然会比坝体中部大，因此，此处仅通过应力、速度及加速度的变化规律来对不同测点的动态响应进行分析)。这样的大小规律是符合爆炸冲击波传播理论的。

测点3与炸药同高，其到爆炸中心点的距离也最短，测点2与爆心之间的距离次之，测点4到爆心之间的距离相对而言就比较远，而测点1距离爆心最远。正是因为4个测点这样的布设位置，爆炸冲击波会最先传播到测点3，使得测点3的应力、位移、速度、加速度等各动态响应在短时间内发生突跃，并且达到最大，其后，爆炸冲击波逐渐向周围传播，依次到达测点2、测点4和测点1，但是由于测点4在地基附近，有地基对其产生的约束，而且该处的混凝土结构体积较大，自身也有比较大的约束作用，而测点1位于坝顶，并没有测点4那样有力的约束，因此，尽管测点1较测点4而言距离爆心更远，但是其所产生的动态响应却可以超过测点4。

5.2 不同比例距离下重力坝整体响应分析

不同比例距离[19]下的爆炸荷载统计[20]结果的最大值、平均值和最小值见表2。

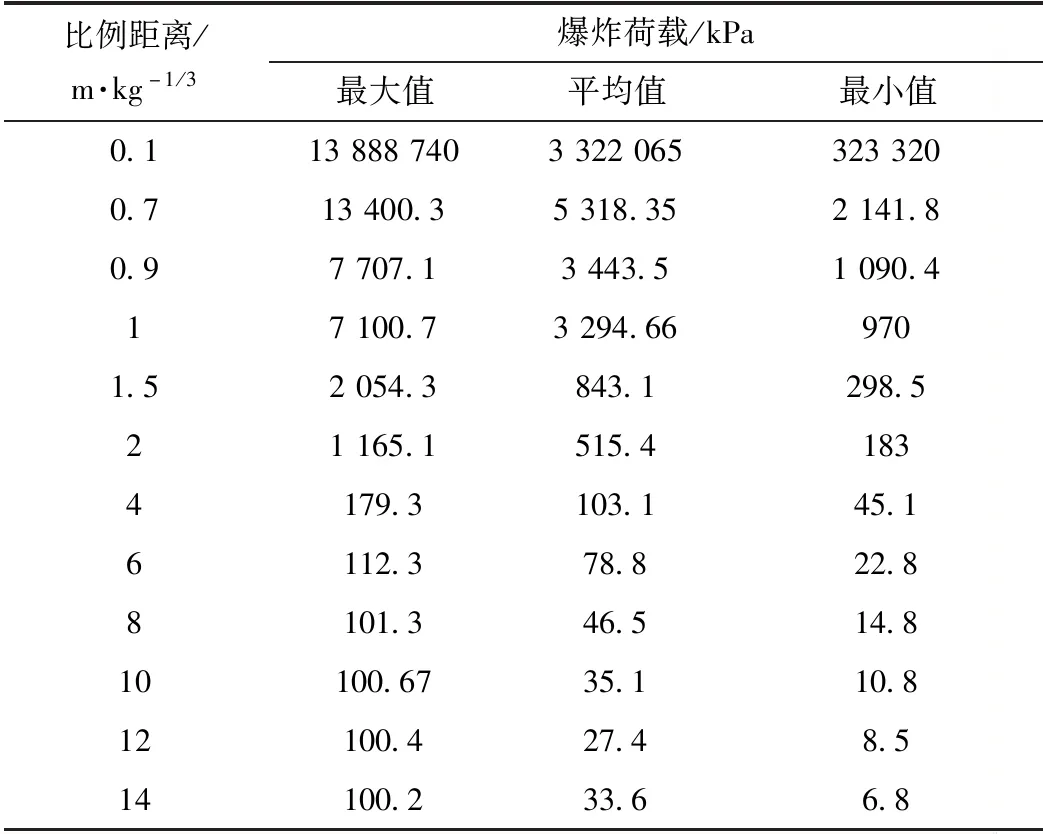
表2 不同比例距离下爆炸荷载统计结果

在不同比例距离的情况下，分别以爆炸荷载的最大值(13 888 740 kPa)、平均值(3 322 065 kPa)和最小值(323 320 kPa)对混凝土重力坝作用时，根据模型计算得到测点3各动态响应的大小及范围，描绘出在不同比例距离和爆炸荷载下，测点3的各种动态响应的变化趋势和变化范围，如图5所示。根据已有资料，坝体对于不同爆炸荷载的动态响应都在此范围之内。其余3个测点采用同一研究方法，本文不再赘述。

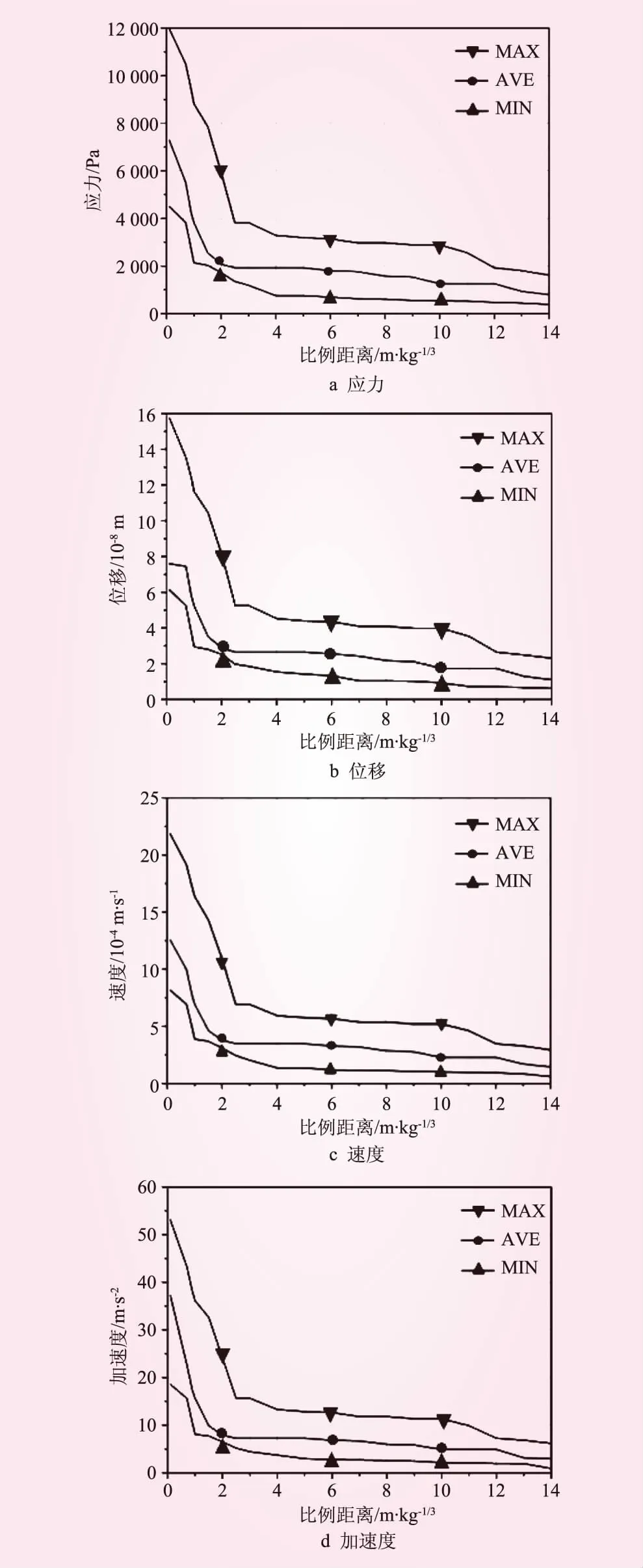
图5 不同比例距离下3号测点的动态响应

6 结 论

本文建立了空中爆炸模型，统计了不同比例距离下的爆炸荷载的最大值、平均值和最小值，分析了混凝土重力坝在不同比例距离下的动态响应，主要结论如下：

(1)从动态响应变化趋势图可以看出，比例距离越小，测点对应的应力、位移、速度和加速度波动性越明显，对坝体破坏越大。

(2)坝体结构失效的主要因素是炸药质量的大小及比例距离。随着比例距离的增大，炸药质量对坝体结构的影响逐渐减小，不同爆炸荷载作用下的动态响应逐渐靠近。在相同爆炸荷载作用下，比例距离越小测点动态响应越大。在相同比例距离下，爆炸荷载越大，测点动态响应越大。

(3)靠近坝底测点受地基和自身的约束，以及混凝土结构的影响，动态响应更具有不确定性。

(4)爆炸荷载的不确定性对坝体结构失效的影响是非常显著的，因此，在爆炸荷载下结构的破坏分析中，必须考虑爆炸荷载的不确定性。