页岩气钻井岩屑运移规律仿真分析
2020-11-09吴鹏程钟成旭王旭东夏成宇
范 宇, 方 永, 吴鹏程, 钟成旭, 王旭东, 夏成宇*
(1.中石油西南油气田公司页岩气研究院, 成都 610000; 2.长江大学机械工程学院, 荆州 434023)
由于水平井和大位移井井身结构的特殊性,此井型的水平井段和大位移井段最容易形成岩屑床,进而导致钻杆高摩阻、高扭矩、拖压,严重时造成卡钻、钻具断落等井眼安全事故,因此提高岩屑运移效率及如何保证井眼清洁是最为关键的技术之一[1-2]。中外学者开展相关研究,黄伟池[3]根据实验现象提出了岩屑的几种运移形式,分析了颗粒直径、钻杆机械转速、注气量等因素对岩屑运移形态的影响。倪晓东等[4]建立了环空岩屑床厚度计算模型,并分析了钻井液排量、岩屑直径、流性指数、钻井液密度、钻杆偏心度、钻杆转速等参数对岩屑床厚度的影响。Nguyen等[5-8]提出了大斜度井及水平井由固定层、移动层、悬浮层组成。张好林等[9]则在研究水平井岩屑运移机理后建立了水平井中岩屑运移临界流速数学模型,并以此分析了钻柱偏心度、转速、井斜角、岩屑粒径及流体黏度对于临界流速的影响。杨善等[10]针对岩屑堆积问题推导出环空岩屑的运动微分方程组,并根据环空岩屑运移综合模拟实验装置得出的数据模拟揭示了环空岩屑运移规律。祝效华等[11]基于气-固两相流和冲蚀理论,建立了三维井眼环空岩屑运移模型,分析了气体钻井中,环空岩屑粒子对钻杆接头冲蚀的影响。刘承婷等[12]根据实验分析了井斜角、入口流量、流体黏度等影响因素对水平环空井段内岩屑运移规律的影响。李永杰等[13]在气固两相流理论的基础上,分析了不同工况下钻杆偏心对气体钻水平井环空岩屑运移规律的影响。孙晓峰等[14]基于Realizablek-ε紊流模型和固液两相流模型模拟了钻柱旋转条件下井斜角、钻井液速度等对岩屑运移的影响。
本研究针对四川长岭和威远地区使用高密度高黏度泥浆(密度2.1 g/cm3)钻井工况下,分析了钻杆转速、排量、岩屑粒径、偏心度、井斜角度等因素变化对环空井筒岩屑体积分数及运移轴向速度的规律影响,为采取合理措施提高岩屑运移效率提供依据。
1 几何模型及参数
以81/2井眼和51/2钻杆为研究对象,钻杆长度为8 m,网格划分采用六面体网格。环空流体域几何模型如图 1 所示,基本参数见表 1。
(1)
式(1)中:ε为钻杆偏心度;e为钻杆中心偏移井筒中心的距离;D为井筒直径;d为钻杆直径。
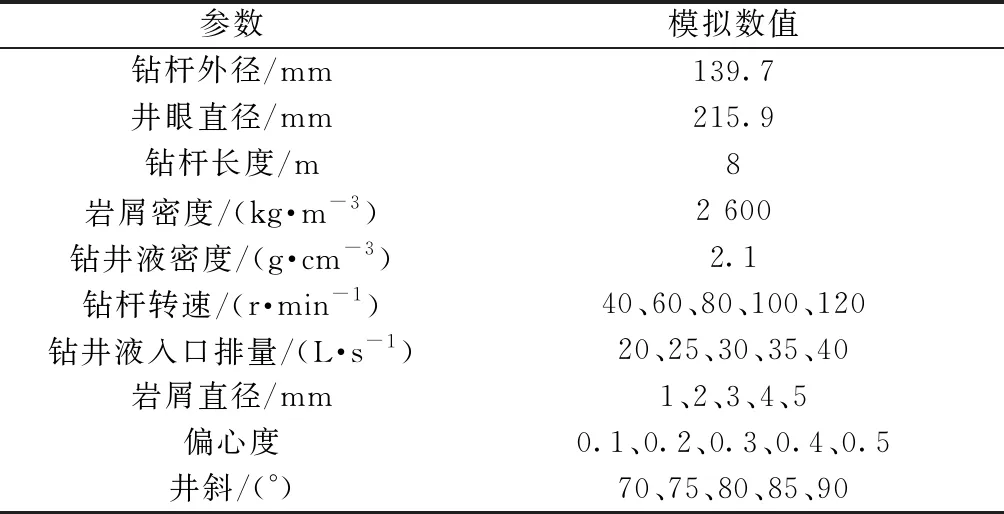
表1 基本参数
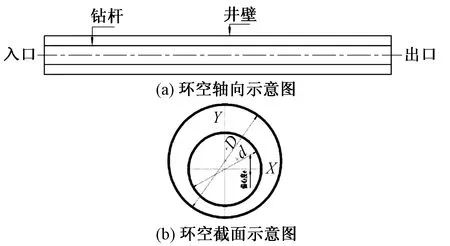
图1 环空模型示意图Fig.1 Schematic diagram of annular model
2 数值模型建立
综合考虑在钻井作业过程中,钻井液携带岩屑由环空返回,环空内部流体为复杂的液-固两相流三维湍流流场,对环空岩屑运移的数值模拟,选用Eulerian多相流模型,并采用RNGk-ε模型[15]。其中,主相为液相,次相为固相和气相。由于井眼环空内岩屑的分布形态会随着时间的改变而改变,因此建立的是三维瞬态模型,为了简化求解过程,对岩屑运移模型作如下假设:忽略环空温度、井底产气产水对钻井液流动的影响;气-液-固三相在流场的流动视为不可压缩流体;忽略岩屑颗粒之间的碰撞与颗粒与壁面之间的碰撞。
2.1 控制方程
(1)连续性方程:
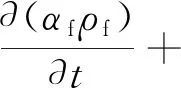
(2)
(2)动量守恒方程:
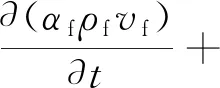
-αfp+·(αfτf)+αfρfg-fdrag
(3)
(4)
(5)
式中:ρf为钻井液密度;αf为钻井液体积分数;vf为钻井液速度;τf为钻井液切应力;fdrag为流体颗粒相互作用力;g为重力加速度;Vpi为第i个颗粒的体积;Δv为计算单元的体积;Fdrag为单个颗粒的拖拽力;m为单元内的颗粒总数。
2.2 湍流方程
考虑到水平井及大斜度井环空岩屑运移流场具有高度不规则、高雷诺数等特点,而 RNGk-ε模型适合解决多相流问题,因此本文选择该模型,湍流输运方程为
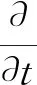
(6)
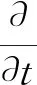
(7)
式中:ρf是钻井液密度,kg/m3;k为湍动能,m2/s2;ε为湍动耗散率,m2/s2;μeff是动力黏度系数,kg/(m·s);Ek是由层流速度梯度而产生的湍流动能,J;Eb是由浮力而产生的湍流动能,J;C1ε、C2ε、C3ε是常量;αk和αε是k方程和ε方程的湍流普朗特数;Sk和Sε是用户定义的源项。其中,C1ε=1.42,C2ε=1.68,C3ε=1.3。
2.3 颗粒运输方程
(8)
(9)
式中:ρp为固体颗粒密度;mp为固体颗粒质量;Vp为固体颗粒速度;dvp/dt为岩屑的惯性力;FD(Vf-Vp)为岩屑单位质量的拖拽力;g(ρp-ρf)/ρp为岩屑的重力;F为其他的力。
2.4 边界条件
研究岩屑床为3层水力模型,即固定层、移动层、悬浮层3部分组成。假设初始设置固定岩屑床高度为10 mm,浓度为80%;移动岩屑床高度为10 mm,浓度为50%,长度均为0.4 m,悬浮层为钻井液。
选取钻杆的一部分作为研究对象,建立数值计算模型,湍流流场的计算采用二阶迎风格式和SIMPLE算法,考虑模拟运算中的收敛性和稳定性,对模型的进口边界条件定义为速度入口,其中液相为钻井液排量;出口边界条件定义为压力出口(pressure),与环境压力保持一致;壁面边界条件定义为:将井壁设为固定壁面,钻杆表面为旋转壁面,湍流壁面条件采用壁面函数边界条件。
3 结果及讨论
3.1 岩屑运移位置及分析
为了得到岩屑在环空中的运移状态,取钻井液密度ρ=2 100 kg/m3,岩屑粒径d=3 mm,黏度μ=30 mPa·s,入口流速v=1.5 m/s,钻杆钻速100 r/min,偏心度0.3。经FLUENT分析,模拟出不同排量岩屑床运移规律和不同时刻的岩屑体积分数云图,分别如图2、图3(a)所示,从图2、图3(a)中可以看出,随着时间的推移,岩屑床运移的距离越来越大,且岩屑床形状逐渐变得扁平而细长,集中的岩屑床逐渐被冲散。

图2 不同时刻岩屑床运移规律Fig.2 Rules of cuttings bed movement at different times
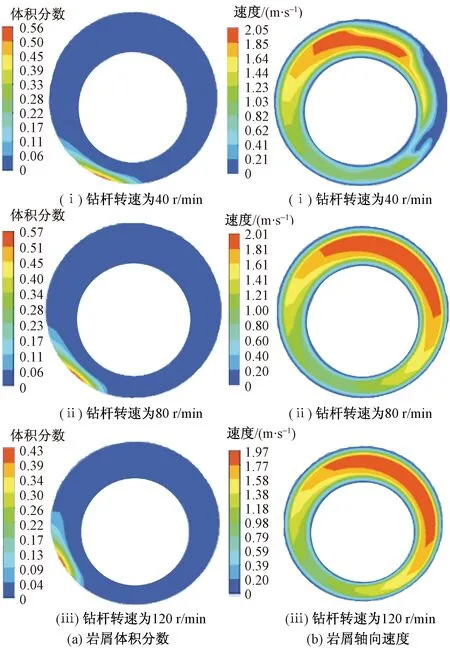
图3 不同转速岩屑运移云图Fig.3 Cloud image of cuttings migration at different speeds
3.2 钻柱转速对携岩的影响
为了研究钻柱转速对岩屑运移结果的影响, 取钻井液黏度为30 mPa·s,钻井液密度ρ=2 100 kg/m3,岩屑粒径d=3 mm。根据实际工况,选取钻杆转速(40、60、80、100、120 r/min),以入口流速v=1.5 m/s数值模拟分析。选取在流速为v=20 m/s下,计算得到岩屑运移3 s时刻,截取该时刻岩屑体积分数以及岩屑轴向速度云图,如图3(a)所示。
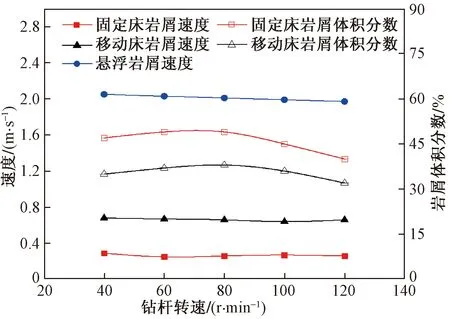
图4 钻杆转速对岩屑运移的影响Fig.4 Effect of drill pipe speed on cuttings migration
如图4所示,钻杆转动对岩屑运移速度影响较小,对岩屑体积分数影响较大。岩屑在钻杆搅动的作用下,岩屑向井筒左侧偏转,随着转速40 r/min逐步增加到120 r/min,岩屑向左侧偏转的高度越来越高,岩屑受到更大向上的合力,使岩屑能更容易悬浮起来,在钻井液的带动下更易流动,导致岩屑床岩屑体积分数变小,岩屑床中越来越多岩屑颗粒进入悬浮层,这说明提升转速抑制了岩屑颗粒在底部沉积的趋势,使更多的岩屑颗粒在脱离固定岩屑床后以更优良的悬浮质状态向出口运移,有利于井筒清洁。
3.3 钻井液排量对携岩的影响
由于排量对岩屑运移距离影响很大,排量越大,岩屑运移距离越大,所以为了研究岩屑体积分数以及岩屑速度,使岩屑床运移到同一位置,不同排量对应不同时刻,岩屑运移位置如图5,截取该时刻岩屑体积分数以及岩屑轴向速度云图,如图6所示。

图5 不同排量岩屑床运移规律Fig.5 The migration law of cuttings bed with different displacement
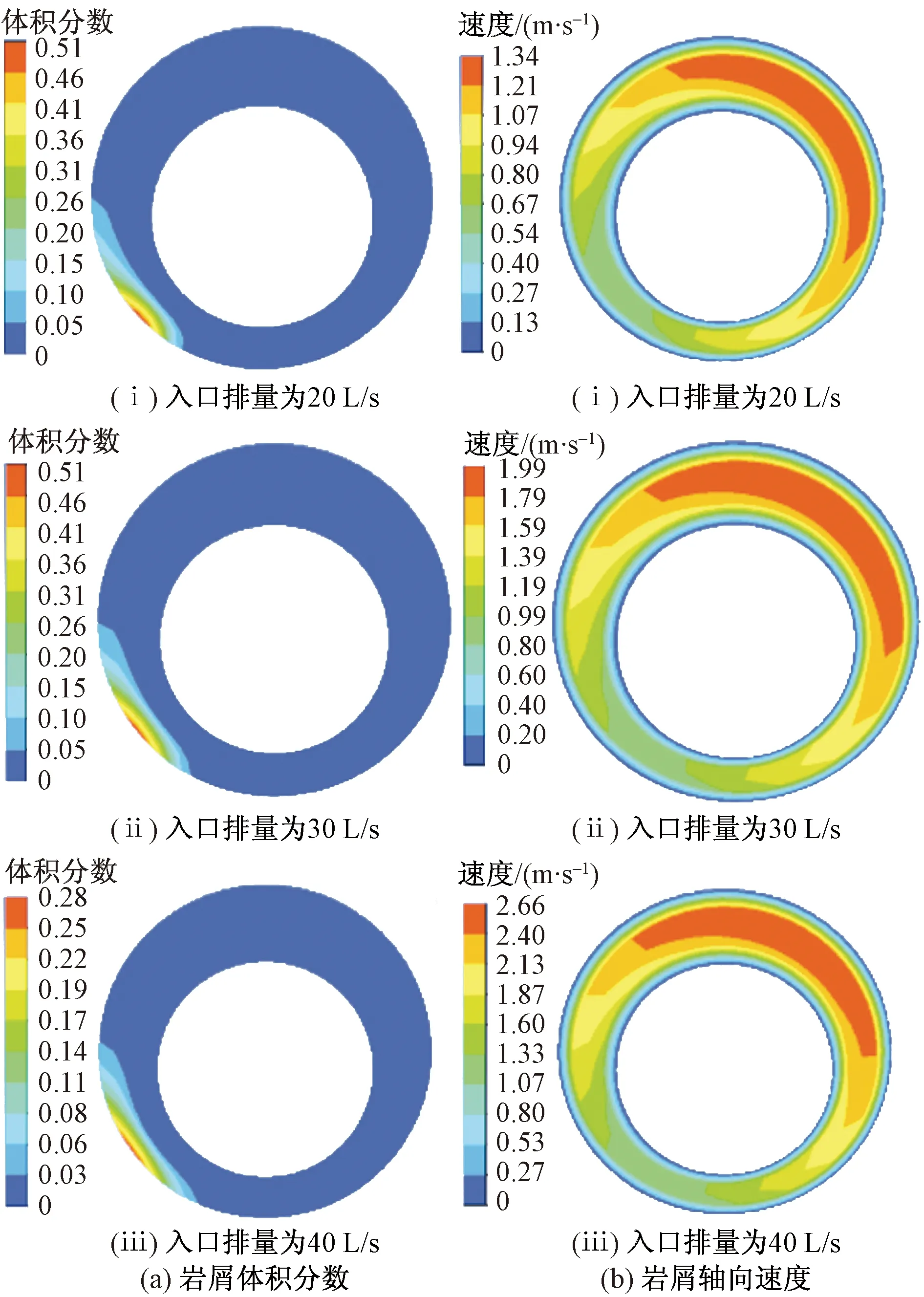
图6 不同排量岩屑运移云图Fig.6 Cloud image of cuttings migration at different displacement
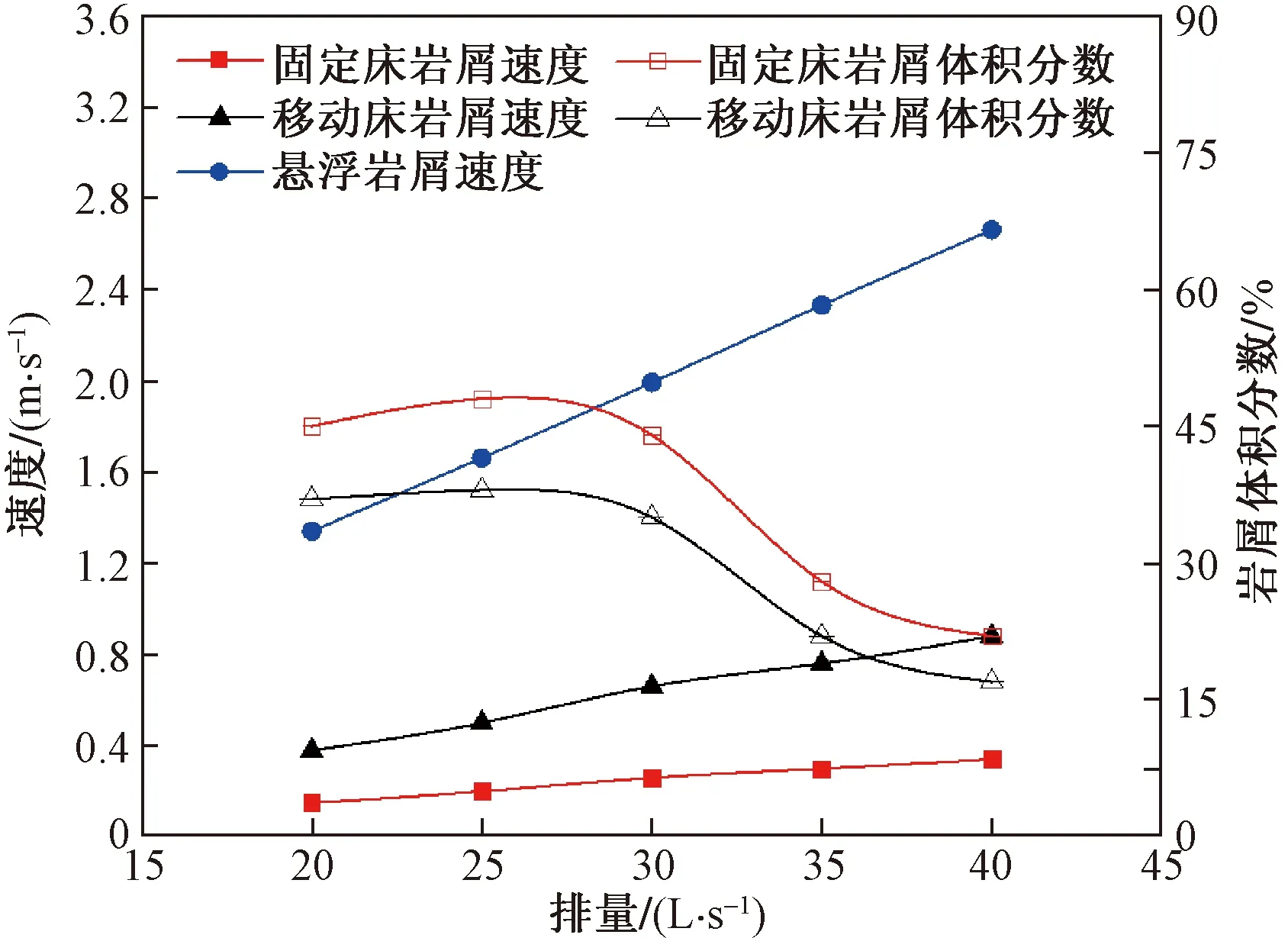
图7 不同排量对岩屑运移的影响Fig.7 Effect of drill pipe speed on cuttings migration
如图7所示,入口排量从20 L/s逐步增加到40 L/s过程中,明显地降低环空中的岩屑颗粒浓度,同时岩屑运移轴向速度明显增大,因为在入口排量较低,转速提供的周向举升力占主导作用,流体参与岩屑床向前推移的轴向速度明显变小,并且被扬起的岩屑颗粒到达环空上方后没有受到足够的举升力,导致岩屑颗粒又回落岩屑床表面,因此仍有大部分岩屑颗粒沉积在环空底部,随着排量的增加,流体与岩屑颗粒交换的动量增加,为岩屑向前运移提供了更大的拖曳力,因此在轴向上能够加速原本作悬移质运动中的岩屑颗粒的轴向运移。说明在转速一定的情况下提高入口排量能够增加流体的携岩能量,从而有效提高井筒内岩屑颗粒的运移效率。
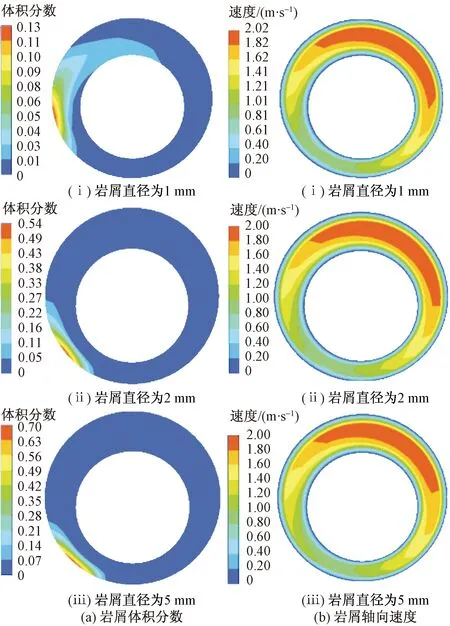
图8 不同岩屑直径岩屑运移云图Fig.8 Cloud image of cuttings migration at different cuttings diameters
3.4 岩屑颗粒直径对携岩的影响
图8(a)、图8(b)分别为岩屑运移3 s时刻岩屑体积分数以及岩屑轴向速度云图。由图8(a)可以看出,岩屑粒径越小越容易被钻杆带到悬浮层,且体积分数越小。由图8(b)看出,岩屑粒径大小改变对岩屑速度影响不大。
如图9所示,岩屑颗粒直径从1 mm逐步增加到5 mm过程中,岩屑颗粒直径对岩屑运移轴向速度影响较小,对岩屑体积分数影响较大。说明大部分岩屑越易沉积在井筒下部。在钻杆转速一定的情况下,岩屑粒径增大,钻杆转速不能够提供足够的离心力和流体的浮力,岩屑到达环空上方后没有受到足够的举升力,导致岩屑颗粒又回落岩屑床表面,岩屑不易进入悬浮层,被钻井液流体带走,因而可以看出粒径的增加明显增大了井筒内岩屑床的厚度,不利于井筒清洁。
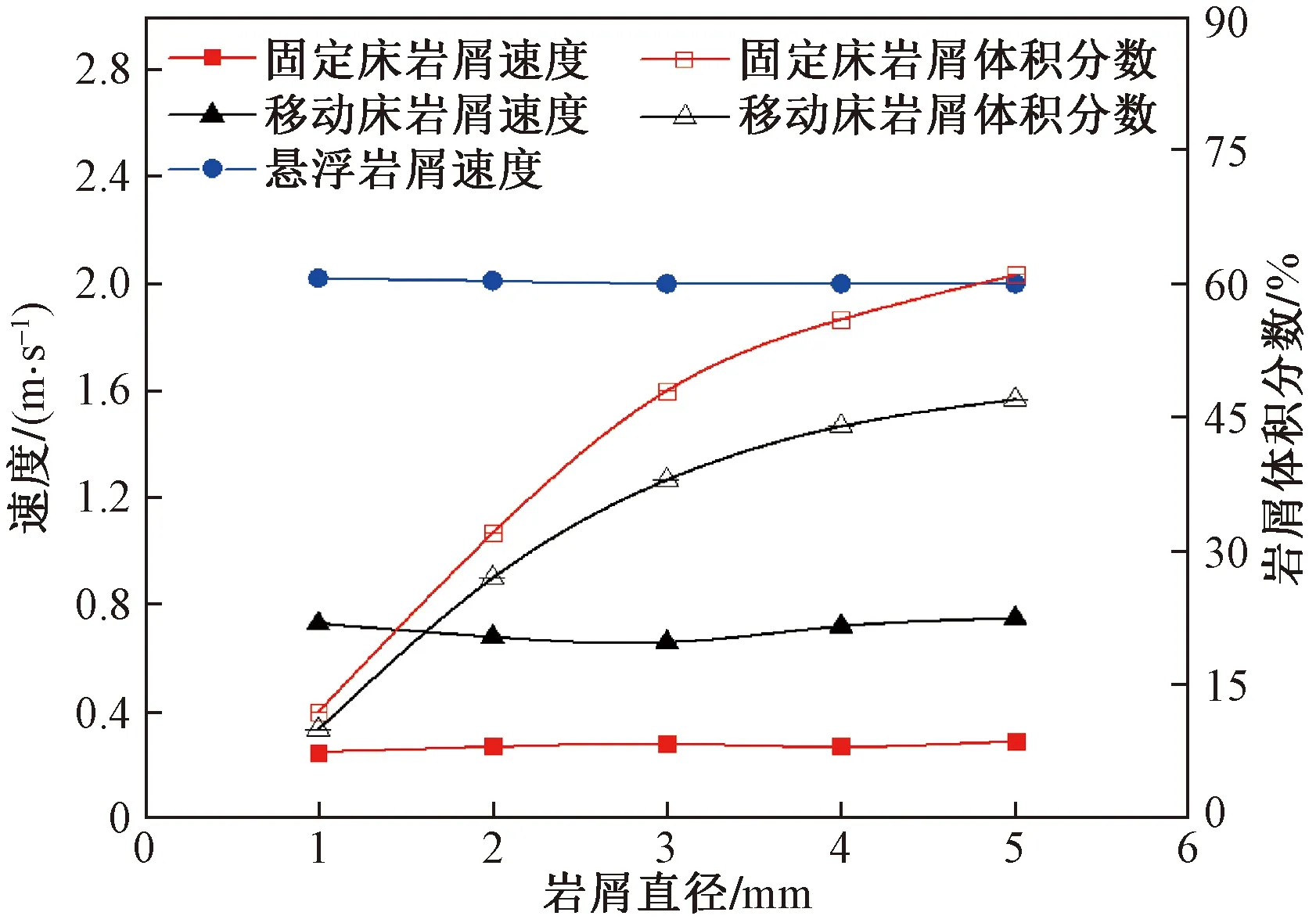
图9 不同岩屑直径岩屑运移的影响Fig.9 Effect of different cuttings diameters on cuttings migration
3.5 不同偏心度对携岩的影响
图10(a)、图10(b)分别为岩屑运移3 s时刻岩屑体积分数以及岩屑轴向速度云图。由图10(a)可以看出,偏心度越大越容易被钻杆带到悬浮层,且体积分数越小。由图10(b)看出,偏心度越大,岩屑轴向速度越大。
如图11所示,结果表明钻杆偏心度对岩屑运移轴向速度和岩屑体积分数影响较大。随着偏心度的不断增加,岩屑床的体积分数不断减小,在完全
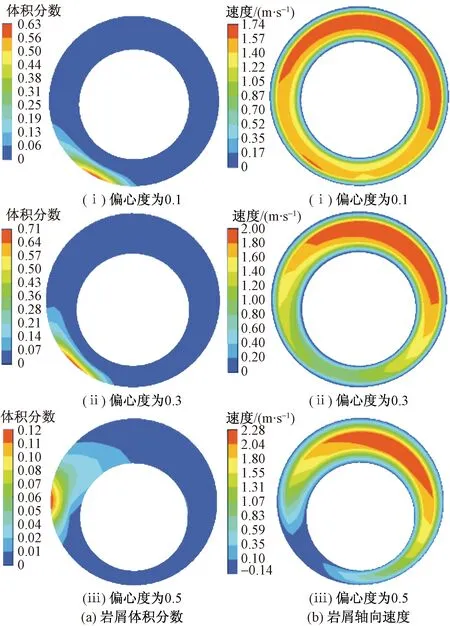
图10 不同偏心度岩屑运移云图Fig.10 Cloud image of cuttings migration at different eccentricity
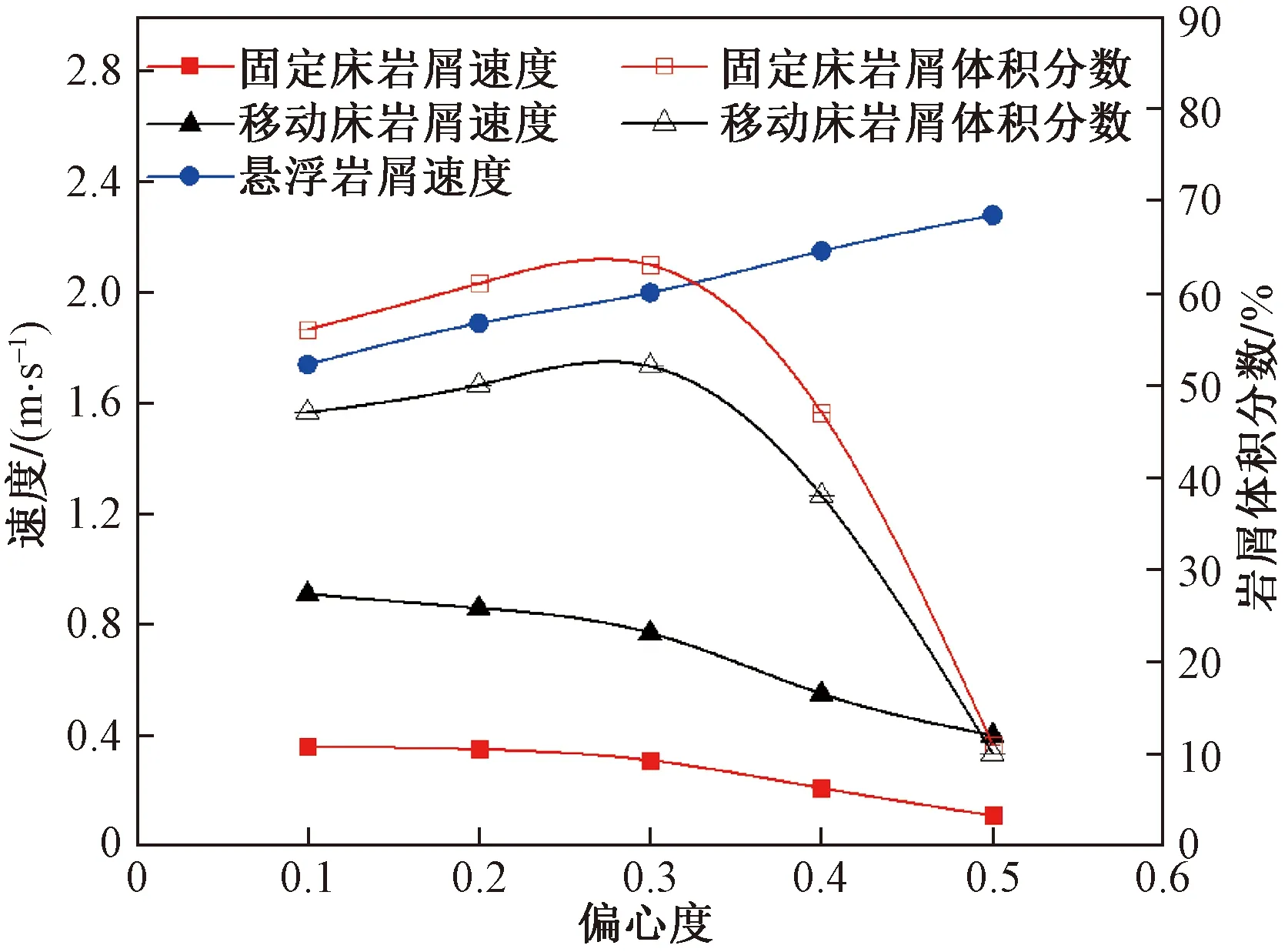
图11 不同偏心度岩屑运移的影响Fig.11 Effect of different eccentricities on cuttings migration
偏心的情况下,固定岩屑床体积分数达到了11%,移动岩屑床的体积分数则为10%,悬浮岩屑速度随着偏心度的增大而增大,说明钻杆偏心度的增大,钻杆越接近井筒底部,对岩屑床搅动越大,岩屑易进入悬浮层,被钻井液流体带走。因而可以看出偏心的增加明显降低了井筒内岩屑床的厚度,提高岩屑运移能力。
3.6 不同井斜对携岩的影响
图12(a)、图12(b)分别为岩屑运移3 s时刻岩屑体积分数以及岩屑轴向速度云图。由图12(a)可以看出,井斜角度越大体积分数越小。由图12(b)看出,井斜角度越大,岩屑轴向速度越小。
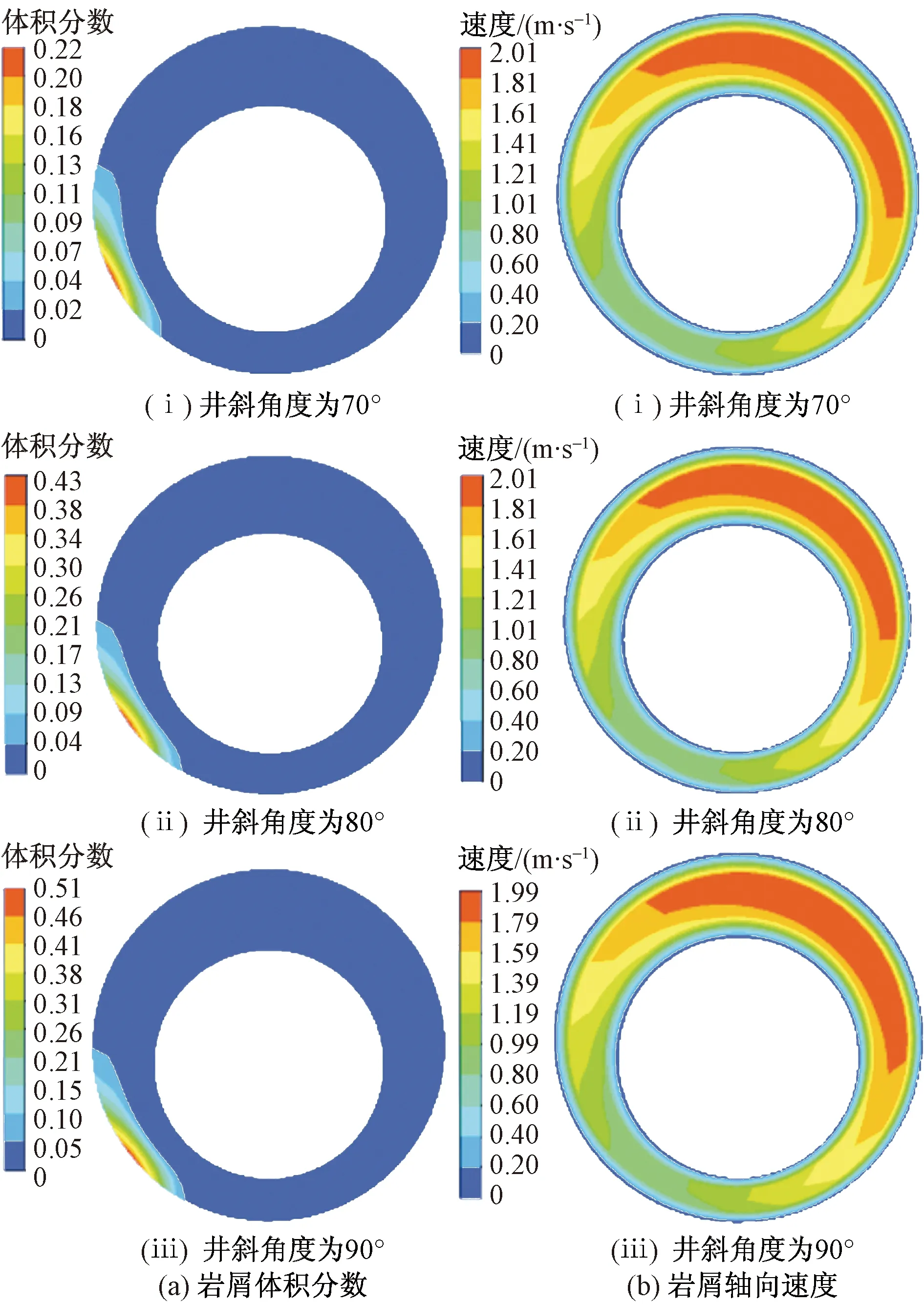
图12 不同井斜岩屑运移云图Fig.12 Cloud image of cuttings migration at different deviations
如图13所示,井斜角从70°逐步增加到90°过程中,井斜对岩屑运移轴向速度影响较小,对岩屑体积分数影响较大。随着井斜角的增加岩屑体积分数增加,说明在水平井逐渐倾斜的过程中,由于钻井液轴向流动对颗粒产生的拖曳力方向与岩屑颗粒的重力方向夹角由垂直逐渐变大,同时重力对岩屑颗粒产生的阻力进一步减小,因此岩屑颗粒受流体的相对悬浮作用力逐渐增大,在井壁下侧沉积的趋势减弱。井斜角的增加使更多的流速用来抵消重力带来的影响,但对岩屑流速和钻井液流速影响不大。
4 结论
根据钻井过程中岩屑运移的情况,充分考虑了钻杆转速,钻井液排量,岩屑颗粒直径,偏心度,井斜的影响,建立了页岩气水平及大位移井岩屑运移模型,采用二阶迎风格式和SIMPLE算法求解,分析岩屑运移的仿真规律。
通过对页岩气井岩屑运移仿真的分析,结果表明:钻柱转速的提高,对井壁下的岩屑有一定搅拌作用,有利于井筒清洁;钻井液排量对岩屑运移速度影响较大,增大排量,能够增加流体的携岩能量,从而有效地提高井筒内岩屑颗粒的运移效率;岩屑粒径大小增大,井筒内岩屑床的厚度增加,不利于井筒清洁;偏心度的增加,对岩屑床搅拌作用更明显,降低井筒内岩屑床的厚度,提高岩屑运移能力;井斜角的增加,岩屑受到流体的拖拽力与浮力夹角越大,岩屑越易沉积井筒下部,井斜有利于井筒清洁。
