抓直线交点 寻巧思妙解
2020-11-06左效平
左效平

一次函数图象相交问题,是一次函数的主要考查点之一,值得深入探究,下面结合一些中考题,向大家介绍有关问题的破解方法,供参考,
一、探究交点的不可能位置
例1(绥化)在同一平面直角坐标系中,直线y=4x+1与直线y=-x+b的交点不可能在( ).
A.第一象限
B.第二象限
C.第三象限
D.第四象限
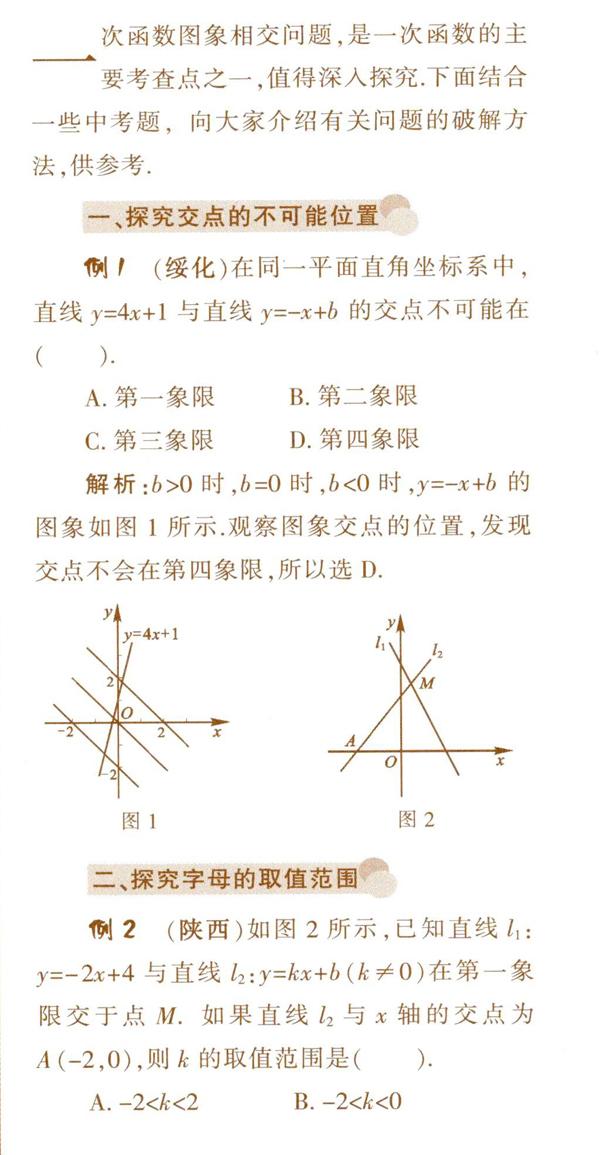
解析:b>0时,b=0时,b<0时,y=-x +b的图象如图l所示.观察图象交点的位置,发现交点不会在第四象限,所以选D.
二、探究字母的取值范围
例2 (陕西)如图2所示,已知直线l1:y=-2x+4与直线l2:y=kx+b(k≠0)在第一象限交于点M.如果直线l2与x轴的交点为A (-2,0),则南的取值范围是( ).
A.-2
B.-2
因为交点在第一象限,所以k的取值范围是0
三、探究代数式的值
例3(贵阳)若直线y=-x+a与直线y=x+b的交点坐标为(2,8),则a-b的值为( ).
A.2
B.4
C.6
D.8
解析:因為直线y=-x+a与直线y=x+b的交点坐标为(2,8),所以8=-2+a,a=10;8=2+b,b=6.所以a-b=4,选B.
四、根据图象确定不等式(组)的解集
例4 (十堰)如图3,直线y=kx和y=ax+4交于点A(1,k),则不等式组kx-6
解析:若将直线y=kx向下平移6个单位,得到直线y=kx-6.如图4,设直线的交点为D.
由直线y=kx和y=ax+4交于点A(1,k),所以知ax+41.且a=k -4.
五、探求直线与线段的关系
例5 (大连)在平面直角坐标系中,点A,B的坐标分别为(3,m),(3,m+2).若直线y=2x+b与线段AB有公共点,则b的取值范围为 ____(用含m的代数式表示).
解析:如图5,当直线y=2x+b经过点A(3,m)时,b=m-6;当直线y=2x+b经过点B(3,m+2)时,b=m-4.所以,若直线y=2x+b与线段AB有公共点,则b的取值范围为m-6
