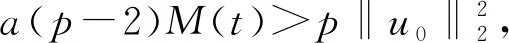一类基尔霍夫型非线性抛物方程解的存在和爆破
2020-11-06黄瑶,石鹏
黄 瑶,石 鹏
(贵州民族大学 数据科学与信息工程学院,贵阳 550025)
0 引言
基尔霍夫(Kichhoff)方程在很多领域中都有广泛应用,在利用数学方程建立物理模型的过程中总能找到相关的理论研究.在过去的几十年里,学者们越来越关注基尔霍夫型问题的研究,基尔霍夫项经常出现在双曲线、椭圆型以及抛物线等不同类型的偏微分方程研究中[1-4].其中最原始的还是基尔霍夫本人在1883年提出的下列基尔霍夫模型:

式(1)是著名的弹性弦自由振动的D’Alembert波动方程的推广,其中:L为弹性弦的长度,h为横截面积,ρ为质量密度,P0为初始张力,E为杨氏模量.
近几年,基尔霍夫方程在非线性偏微分方程的各项课题研究中十分活跃,在人口动力学、非牛顿力学、弹性理论等诸多领域方面,都能看到这类方程的广泛应用.其中,2013年,Liu X和Sun Y[5]用Nehari流形的方法研究了一类基尔霍夫型微分方程两个弱解的存在性.2014年,Liang、Li和Shi[6]利用拓扑度理论和变分方法研究了一类有渐近行为的基尔霍夫型微分方程正解的存在性.2018年,张申贵[7]利用临界点理论研究了一类变指数基尔霍夫型方程的无穷多解.2019年,刘紫玉和韩伟利[8]用变分原理和山路引理证明了组合非线性项的基尔霍夫方程径向解的存在性.
通常对非局部项做一定的改进,就可以得到一类新的方程.为了得到本研究中的一类基尔霍夫型非线性抛物方程,首先观察下面这个含有基尔霍夫项的波动方程:
当α=0时,变成了一类含有基尔霍夫型的抛物方程:

本研究对式(3)抛物方程赋予初边值问题,得到下列一类基尔霍夫型非线性抛物方程:

其中:Ω∈RN(N≥1)是具有光滑边界∂Ω的有界域,1 应用位势井理论和变分法,可以研究当初始能量分别处于亚临界、临界和超临界时解的整体存在性和有限时间爆破的结果,本研究着重讨论亚临界状态J(u0) 为了更加方便地进行研究,首先引入位势井,对于式(4),定义下列的能量泛函J(u)和Nehari泛函I(u),然后研究它们的功能和基本属性. 定义Nehari流形 再分别定义位势井和相应的集合如下: 引理2[10]假设u(x,t)是式(4)的弱解,0 1)如果I(u0)>0,则u(x,t)∈Wδ; 2)如果I(u0)<0,则u(x,t)∈Vδ. 其中,对于δ>0,可定义下面修改后的函数集合以及位势井: 引理4[11]假设0 M″(t)M(t)-(1+γ)(M(t))2≥0,γ>0. 证明首先构造式(4)的近似解为 和 因此,对于足够大的m以及0 和I(um(0))>0成立. 这意味着对于足够大的m来说um(0)∈W. 因此,由反证法证明了对于足够大的m和t∈[0,T],有um(t)∈W. 由式(17),对于足够大的m来说,有I(um(t))>0,则由式 及式(17),得到 上式对于足够大的m和∀t∈[0,T]均成立,且得到以下不等式 因此,由对角化知,存在一个u和{um}的子序列,使得 在式(13)中固定j,并令m=v→∞得到 和 由引理1和引理2,得到um(t)∈W.∀0≤t<∞,这就证明了um(t)∈W. 由式(21)、(22)、(24)的收敛性,根据序列收敛原理以及式(5)中J(u)的定义,得出式(11)成立.因此,证明了极限函数u=u(x,t)是式(4)的弱解. 定理2假设a,b>0,1 证明令u为式(4)的弱解且满足J(u0) 因为 如果p>4,由式(11)、(28)、(29)可以得到 因为 所以 利用Schwart不等式,得到 接下来,我们对如下两种情况进行讨论即可. 情形1:当J(u0)≤0时,则 现在证明∀t>0,有I(u)<0.那么一定存在一个t0>0使得I(u(t0))=0和I(u(t))<0,其中0≤t
1定义和引理













2 主要结果