基于程度化思想的假设检验p值教学研究*

魏立力 刘国军

（宁夏大学 数学统计学院，宁夏 银川 750021）

一、引言

假设检验是统计推断的重要形式之一,是依据样本提供的信息对总体某个假设做出判断的过程,在医疗卫生、工程、经济、农业等诸多领域都有广泛应用。一般统计学教材中采用两种方式呈现检验过程,一为临界值法,二为p值法。临界值法是通过比较检验统计量观测值与临界值的大小,判断观测值是否落入拒绝域,从而做推断。而p值法是根据给定的样本观测值,计算输出一个p值,p值越小,拒绝原假设的理由越充分。可见p值反映了拒绝原假设的程度,可以比较精细地反映决策风险,使用p值法有利于走出传统的二值逻辑,树立程度化思想,也更契合人脑智能特征。

由于统计软件都可以输出p值,在应用领域多用p值做判断。但在具体应用中,还是存在滥用、误用及误解p值的现象。近年来,一方面,应用研究工作者在展示研究成果时不遗余力地追求(甚至操纵)更小的p值,以说明自己成果的“显著性”；另一方面,统计学术界针对p值进行科学推断的弊端展开了激烈的学术争论[1-3],这些现象引起了国际统计学界的高度重视。比如2016年美国统计学会(ASA)发表了一个关于统计显著性和p值的六项官方声明[4-5],国内一些学者也对该声明做出了不同角度的解读[6-9]。

在多年教学实践过程中发现,很多学生将假设检验理解为二值决策,能够理解用临界值确定的拒绝域和接受域,但基于p值往往难以理解和解释检验过程,究其根源是缺乏程度化思想。这就出现了在应用层面广泛而频繁地使用着的p值,在教学层面却是概念模糊、逻辑不清的尴尬局面。

本文从假设检验教学的视角,针对许多统计学教材中关于p值的叙述不够详尽的现象,基于程度化的思想,对p值进行研究。阐述p值的定义,举例说明计算方法,指出如何用p值进行决策等。运用本文观点,容易理解ASA关于统计显著性和p值的六条声明。

二、p值的定义与计算

（一）p值的定义

p值是一个基于特定假设和样本观测值进行统计推断的工具。从工具使用者的角度看,p值反映了原假设成立时研究者得到现有样本观测的不可能程度。p值越小,说明原假设为真时获得现有观测结果的概率越小,小到一定程度,就应该拒绝原假设。从应用的角度说,p值越小,表明结果越显著。p值和显著性水平关联后可以得到如下定义：

定义1,在一个给定的假设检验问题中,利用现有样本值能够拒绝原假设的最小的显著性水平称为检验的p值。

这个定义告诉我们,p值有两个要素：样本观测值和假设分布。先用样本观测值计算检验统计量的值,再由假设分布计算和确定相应的p值。对于不同的样本观测值,相应的p值也不同,可见p值是一个随机变量[10],其值与当下样本观测值有关,它的大小反映了利用现有的样本值能够拒绝原假设的程度。

ASA的声明中给出的p值非正式定义是：p值就是基于某个特定统计模型之下,对于样本的某个统计汇总(Statistical Summary,如,两个对照组的样本平均值之差)与实际观测值“相等或更极端”的概率。

理解这个描述的关键是把握“相等或更极端”的含义。这有赖于具体的检验统计量,该统计量取值的方向性(大或小)决定了其“更极端”的含义。如果该统计量的取值越大,对对立假设越有利,则“相等或更极端”就是指该统计量“大于等于”现有的观测值；反之,如果该统计量的取值越小,对对立假设越有利,则“相等或更极端”就是指该统计量“小于等于”现有观测值。

p值的具体计算依赖于原假设中的概率分布,因而除非原假设是简单假设,否则p值一般不是一个值,而是原假设中参数的函数,实用中取其上确界。具体而言,考虑参数假设检验问题H0：θ∈Θ0↔ H1：θ∈Θ1,此时确定p值的方法由下面定义给出。

定义 2,设 T(X)是一个检验统计量,如T(X)的值越大表示H1为真的依据越充分,则对于样本观测值x,定义该检验的p值为

如T(X)的值越小表示H1为真的依据越充分,则对于样本观测值x,定义该检验的p值为

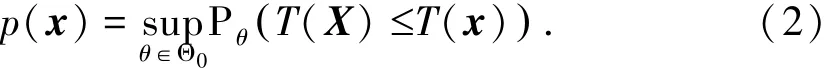
上述定义给出了p值的具体计算公式,但计算上确界时可能会有困难。下面我们举例说明一般情况下的计算问题。

（二）p值的计算

例1 设X1,X2,…,Xn是来自N(μ,σ2)(σ2未知)的简单随机样本,考虑检验问题

这可通过t分布的分布函数得到。上面倒数第二个等式成立是因为上确界在μ=μ0处取得,去掉下标是因为这个概率不依赖于参数。

例2 某种治疗方法对某种疾病的治愈率仅为25%。现有一种新的治疗方法,我们想测定是否对同样的疾病有更好的效果。以θ记这种新方法的治愈率,而提出假设检验问题：

H0：θ≤ 0.25 ↔H1：θ＞0.25。

这里,原假设表示新方法治愈率不比旧的好,而备择假设则表示新的优于旧的。

我们选择20名合格患者,都用这种新方法治疗,以X表示其中治愈者的人数,则X取值越大对原假设H0越不利,对备择假设越有利,因而p值的计算还套用定义3中公式(1)。此时参数为θ∈Θ=[0,1],原假设对应的Θ0=[0,0.25],检验统计量X～B(20,θ),X的所有可能取值及其p值见下表1。

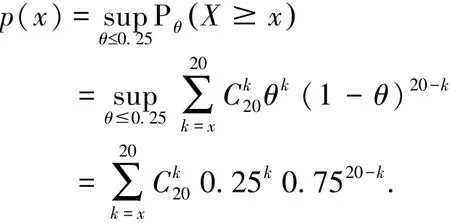
表1 X的所有可能取值及对应的p值

上面的例子中,确定上确界都不太困难,在比较复杂的情形中(比如在例1、例2中的原假设改为一个有限区间),求上确界也许就没有这么简单了。在研究性教学过程中,我们建议学生使用微积分或优化工具。

三、p值的本质与可能的误解

p值就是在零假设条件下对数据特征的总结分析,p值提供的是实际数据与零假设不相容的证据,p值越小,说明在零假设成立的条件下,得到现有数据的概率越小,越有把握拒绝原假设,可见p值反映了程度化思想。在实际操作中,如果必须做出二值决策,则事先指定显著性水平,如果p值小于这个水平值,则拒绝原假设。“显著”和“不显著”的二分法有时候令人费解。比如p值分别等于0.048和0.052,二者区别并不明显,但前者被认为是显著的,后者却被认为是不显著的。需要特别注意的是,当单次实验中得到“刚好显著”的结果,比如p=0.049,以此宣称有所发现时,犯错的概率仍然可能很高。

关于p值本身,经常存在如下三个误解：

第一个误解是将p值看作“在得到现有样本观测值条件下原假设成立的概率”。在经典统计学的观点下,假设是一个关于总体未知部分的陈述,这个陈述要么正确,要么不正确,两者必居其一,不存在随机性,不能说假设成立的概率。这种误解将两个条件概率P(A|B)和P(B|A)混淆。对这两种不同概率的混淆,是导致p值被误解的核心所在。这被称为条件概率倒置错误。事实上,对假设给出概率描述只可能在贝叶斯统计中完成。

第二个误解是“如果决定拒绝原假设,则p值就是作出错误决定的概率”。这有点相似于拒真概率,但事实上,如果拒绝原假设,则错误就是指原假设为真,因此其概率就是原假设为真的概率,这种误解和第一种误解本质上相同。

第三个误解是“如果将试验重复很多次,则试验获得显著性结果的频率大约为1-p”。这里的获得显著性结果,就是拒绝原假设,将1-p误解为试验获得显著性结果的频率,也就是显著性结果可以被重复的概率。事实上p值依赖于试验结果,不同的观察值一般对应不同的p值,p值不能被重复。p值从来没有被证明可以用来接受某个假设,即使是拒绝假设,也是基于某个样本得出的结论,当样本变动时,结论很可能也会变动。

如前所述,影响p值的两个要素是当下的样本观测值和原假设对应的分布模型。前者包括了样本容量,从前面例1我们可以看出：当n增大时,统计量的观测值也趋于增大,因而导致p值减小,只要n足够大,p值就可以足够小,由p值检验几乎总是拒绝原假设。这种现象具有一般性,因此,在假设检验问题中,报告p值的同时,应特别注意样本容量的大小,同样的p值在不同的问题中,或者问题相同但样本容量不同,可能具有完全不相同的信息。

四、结语

假设检验的类型很多,有参数检验与非参数检验,这些检验的拒绝域各不相同,背景也相差很大,如果用拒绝域法,则情况比较繁杂,但只要能算出p值 (一般统计软件中都输出p值,有的用“p-value”表示,有的用“Sig.”表示),都可用 p 值对原假设作出判断,而不管它们的背景有多大的差异,这正是p值的通用性。

笔者利用本科生和研究生统计学教学实践和研究结果,总结了p值的两个定义,举例说明了p值的计算和可能的困难,阐述了p值的本质和可能的三种误解。采用本文观点理解ASA的声明中包含的六条准则是水到渠成的事情。

在实际使用假设检验时,使用者首先应该给出p值,同时给出试验的规模,并将其理解为现有样本数据(包括数据规模)与原假设不一致性的程度；其次尽量避免使用“显著”或“不显著”(或拒绝与接受)的二值逻辑进行判断；最后,置信区间和功效可以给读者提供研究结果可靠程度的更多的判据。另外也可以使用贝叶斯检验方法,对同一个数据使用多种方法进行分析。结果越是不同,就越有可能出现重大的发现。