基于特征相关分析的内燃机故障诊断方法

张 波，韩光谱，冯丞科，龚 伟，周 仁

(中国石油西南油气田公司 重庆气矿工艺研究所，重庆 400021)

0 引言

内燃机故障诊断常用的分析处理方法有时域分析法、频域分析法、角域分析法和时频分析法等[1-2]，通过不同的分析方法都能够提取表征不同信息的特征。融合不同特征来评估内燃机的状态，能够有效地提高内燃机故障诊断的准确性、有效性和可靠性。文献[3]提取多项时域指标和频域特征，再利用PCA选取敏感特征实现降维处理，最后利用SVM进行训练和测试，实现故障诊断。文献[4]通过特征融合技术构建多域特征，再根据融合特征进行故障诊断，从而大大提高了故障诊断的精确度。由于所有的特征都是用来表征同一信号的，虽然特征提取方法不同，但存在特征对信息重复表达的可能性。提取的特征越多，重复表达的可能性越高，也就是出现特征相关的可能性越高。在没有剔除高度相关特征的情况下，直接对特征进行维度约减，不但影响最终的信息表征效果，而且会造成计算资源的浪费。

综上，本文提出一种基于特征相关性分析的内燃机故障诊断方法。通过对多域特征的相关性分析，对关联性高的特征组合进行择一保留，得到弱相关的多域特征集合；然后基于主成分分析法(PCA)并结合k近邻学习(kNN)算法实现对内燃机故障的准确诊断。

1 多域特征提取

1.1 时域及频域特征提取

监测系统采集到的振动信号是以时间为横轴、幅值为纵轴的时域信号。根据时域分析方法，主要提取时域信号的统计特征和波形特征等，具体计算公式[5]如下：

其中：TFi为时域信号特征；xi为第i个采样点对应的幅值；N为一个周期所具有的数据点数。

傅里叶变换是经典的频域分析方法，可以把一个周期信号表示成多个周期函数(基函数)的相加，也就是将信号分解为频域里各种不同频率的信号。从频域方面分析，同样提取频域信号的统计特征和波形特征等，具体计算公式如下：

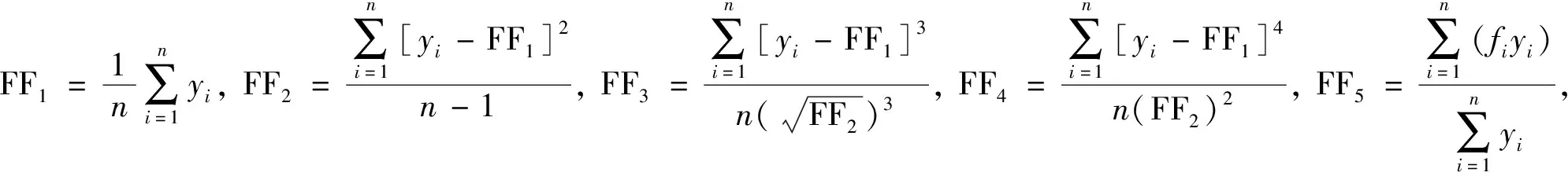
其中：FFi为频域信号特征；yi和fi分别为变换之后的幅值和频率；n为抽样点序号。

1.2 时频域特征提取

利用VMD方法可以将信号分解成具有不同频率特性的固有模态分量(IMFs)，实现信号的频域分割和各分量的有效分离。为了提取振动信号的有用信息，本文选择将振动信号分解成4个分量信号。然后，计算各分量信号的幅值能量和瞬时排列熵作为振动信号的时频域特征。分量信号的幅值能量可以根据以下公式计算：

(1)

其中：uj(n)为分量信号；FFT(uj(n))为各分量信号的快速傅里叶变换结果。对分量信号进行如下幅值处理可以得到瞬时能量分布IEDj(n)：

(2)

其中：aj(n)为各分量信号的瞬时振幅函数。将IEDj(n)结合排列熵计算公式即可得到瞬时排列熵IPEj。

2 基于特征相关分析的内燃机故障诊断方法

2.1 特征的相关性分析

综合上述所有常用特征形成多域特征集合，该多域特征集合一共拥有39个特征，具体包括18个时域特征、13个频域特征和8个时频域特征。为了定量不同特征间的相关性，本文采用协方差方法来衡量两个特征X与Y间的协同变化关系，如式(3)所示：

Cov(X,Y)=E{[X-E(X)],[Y-E(Y)]}.

(3)

其中：E(X)、E(Y)分别为X与Y的期望。当Cov(X,Y)>0时，表示X与Y正相关；当Cov(X,Y)=0时，表示X与Y不相关；当Cov(X,Y)<0时，表示X与Y负相关。

对于多域特征集合，利用Pearson相关系数来衡量两个变量线性相关的程度，如公式(4)所示：

(4)

其中：D(X)、D(Y)分别为X与Y的标准差。相关系数的大小在-1和1之间变化。

2.2 考虑特征相关性的内燃机故障诊断方法流程

针对内燃机缸盖振动信号，开展相关的时域、频域、时频域分析并提取相应的特征，形成多域特征集合。基于多域特征集合内不同特征间的相关性分析，可以了解不同特征间的线性关联关系。通过选择合适的相关系数阈值，对强相关特征组合进行择一保留操作，可以得到弱相关的多域特征集合。对弱相关的多域特征集合进行PCA[6]特征降维并结合kNN[7]算法实现对内燃机的气门间隙故障进行诊断，故障诊断方法流程如图1所示。

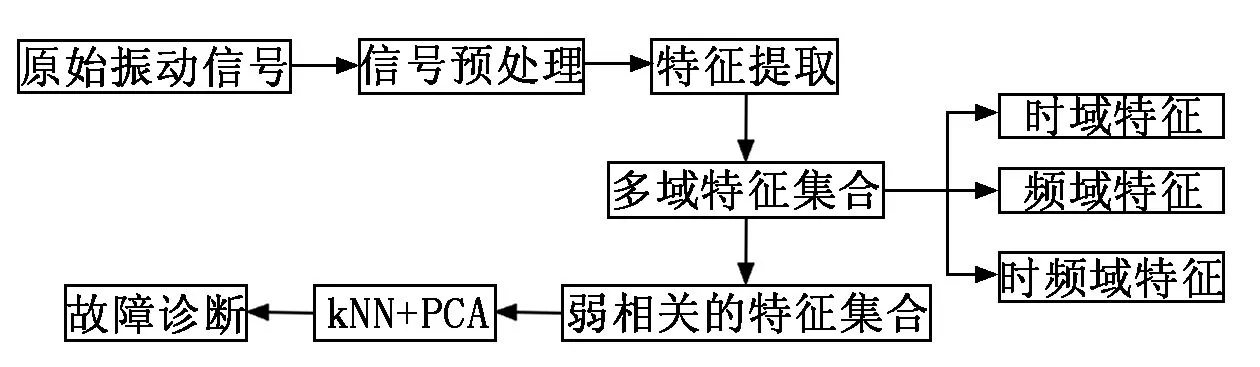
图1 考虑特征相关性的内燃机故障诊断方法流程

3 试验结果

为了说明本方法的适用性与准确性，本文采用内燃机的气门间隙异常模拟实验进行验证，并将所得结果与其他方法所得结果进行对比分析。

3.1 气门间隙模拟实验

故障模拟实验在型号为TBD234的V形12缸内燃机上进行。内燃机的传感器布局如下：在内燃机缸盖布置加速度传感器监测内燃机运行状态下的振动信息，在与内燃机曲轴相连的飞轮上布置涡轮传感器用来确定周期信号采样，在齿轮箱处布置涡轮传感器。通过这些传感器来获取内燃机运行状态的相关信息。

为了研究气门间隙大小对振动信号的影响，通过改变气门间隙大小进行多组实验并采集相应的信号。分别采集气门间隙正常和异常状态下的数据，振动信号如图2所示。

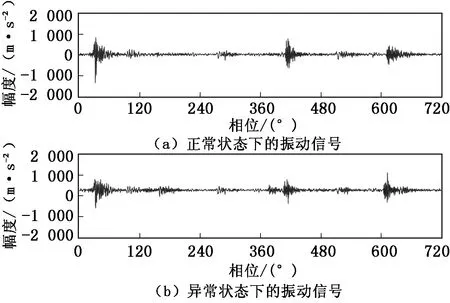
图2 气门间隙正常与异常状态下的振动信号

3.2 考虑特征相关性的特征降维

根据上述特征提取内容，对多域特征集合进行特征相关性分析。假定多域特征集合为{Fi}，i=0,2,…,38,{F0,F2,…,F17}对应表示时域的18个特征，{F18,F20,…,F30}对应表示频域的13个特征，{F31,F33,…,F38}对应表示时频域的8个特征。

混淆矩阵[8]清晰展示了不同特征间的线性关联程度，以0.8作为相关性阈值时，对多域特征集合进行降维处理，最终得到弱相关的多域特征集合为{0，1，2，6，17，21，22，25，28，29，31，33，34，35，36，37，38 }，共17个特征。

3.3 气门间隙异常故障诊断

利用PCA对弱相关的多域特征集合进行特征降维，基于不同的降维结果并结合kNN算法进行气门间隙异常的故障诊断，结果如表1所示。同时，对不考虑特征相关性的多域特征集合进行相同的PCA降维和结合kNN(k=1)算法进行气门间隙异常的故障诊断，结果也列入表1。

表1 基于不同特征维度的不同特征集合的诊断精度

通过上述结果可以看出：基于相同的PCA降维处理，相比强相关的多域特征集合，弱相关的多域特征集合对气门间隙状态的表征效果更好。

4 结论

本文提出了一种考虑特征相关性的内燃机故障诊断方法，根据不同方法提取了多个不同的特征参数，形成多域特征集合；然后对多域特征集合进行特征相关性分析，并对关联性高的特征组合进行择一保留；最后利用PCA进行特征降维并结合kNN算法完成内燃机的气门间隙异常故障的诊断。实测数据分析结果表明：基于特征相关性的降维方法效果显著，结合kNN算法，能够对气门间隙故障进行精确识别。