基于Gabor小波与PSO-SVM的不锈钢焊缝缺陷分类研究*
2020-11-05傅留虎闫耀东柴钰杰李宇琪
傅留虎,赵 娜,闫耀东,张 睿,,柴钰杰,李宇琪
(1.太原科技大学 计算机科学与技术学院,山西 太原 030024;2.山西省机电设计研究院有限公司,山西 太原 030009;3.太原科技大学 信息与技术学院,山西 晋城 048011)
0 引言
由于制作工艺和生产环境等各种因素的制约,在不锈钢焊接过程中难免会产生各类焊接缺陷。及时有效地识别出各类缺陷可以发现隐患,减少相关财产的损失以及为人民的生命安全提供保障[1]。超声检测作为一种应用在焊缝无损检测领域的常用方法[2],依据所提取的超声信号特征的不同来识别判断焊缝缺陷类型,对于评价焊缝结构的安全性具有重要意义[3-4]。
信号特征提取是识别缺陷种类的基础[5-8],常规方法是从超声信号的时域或频域图中提取缺陷特征。但考虑到缺陷超声回波信号的非平稳性,通常会在超声信号的特征提取中运用经验模态分解、小波分析等时频分析方法,以期获得更详尽的特征信息。当前,对于不锈钢焊缝缺陷实现精准分类依旧存在一定的挑战,信号特征提取的稳定性及准确率都有待提高。
近年来,伴随着计算机技术的高速发展,特别是机器学习在自然图像识别领域的成功应用,使得人们开始尝试将其应用于工业检测领域[9-10]。但是,目前机器学习在超声焊缝图像上的应用还比较少。本文以焊缝超声缺陷图像为研究对象,探究利用机器学习对超声图像进行分类的可行性,在利用Gabor小波进行特征提取的基础上,提出了一种基于PSO-SVM的机器学习算法。以常见的五类焊缝缺陷为研究对象开展实验,并将实验结果与其他常规方法进行了比较。
1 数据采集
由于缺乏不锈钢焊缝缺陷数据集,在山西省机电设计研究院有限公司支持下,通过专业检测人员进行焊缝缺陷试样加工,共制备了包括气孔、裂纹、夹渣、未熔合和未焊透五类焊缝缺陷的数据试样,并在山西省机电设计研究院搭建了焊缝缺陷数据采集平台,如图1所示。通过使用KARL DEUTSCH(ECHOGRAPH)探伤仪、Tektronix DPO2024B示波器和2.5P 9x9 K2.5斜探头对缺陷试样进行数据采集,获得了上述五类焊缝缺陷数据共544组。

图1 焊缝缺陷数据采集平台
2 Gabor小波
Gabor小波的提出使得利用Fourier变换能够同时在时域和频域上进行分析,并使非平稳信号的分析变得简单[11]。该种变换将小波变换与小波理论进行有机结合,克服了窗口大小在确定之后不能调焦从而不能对信号进行多分辨率分析的问题[12]。
小波变换在抗光、尺度和方向变化能力方面均有良好的表现,所以其在纹理特征分析和目标识别领域方面应用较为广泛[13]。利用Gabor小波获取超声信号图的特征时,采用不同角度和尺度的Gabor滤波器组成的滤波器组来实现超声信号图的特征提取[14]。设输入图像为I(z),I(z)与Gabor滤波器组φ进行卷积积分后的结果Oμ,v(z)满足式(1):
Oμ,v(z)=I(z)·φμ,v(z).
(1)
其中:v和μ分别为Gabor滤波器的尺度参数和方向参数;φμ,v(z)为Gabor小波变换函数。
为提高计算速度,对式(1)进行快速傅里叶变换,根据卷积定理可得:
F{Oμ,v(z)}=F{I(z)}·F{φμ,v(z)}.
(2)
再利用傅里叶变换得式(3):
Oμ,v(z)=F-1{F{I(z)}·F{φμ,v(z)}}.
(3)
取其幅度信息得其Gabor特征Gμ,v(z)如式(4):
(4)
通过上述几个步骤获得的焊接缺陷超声信号的Gabor特征如图2所示。将缺陷超声时域图的Gabor特征向量首尾连接形成一个列向量,用它作为特征向量。本研究中共有544张焊缝缺陷超声时域图,大小均为128×128,采用40个滤波器组与其做卷积,得到Gabor特征向量M的维数为524 288。为减少计算量,通过均匀采样降低了数据维度。

图2 Gabor小波提取的焊接缺陷超声信号特征
3 粒子群算法优化支持向量机模式识别
3.1 粒子群算法
粒子群算法的思想来源于鸟群的觅食行为,寻找最优解的过程是通过个体间的信息传递与共享完成的[15-16]。该算法具有良好的全局搜索能力,在参数选择和收敛速度上有一定的优势。迭代时,粒子在跟踪到个体极值pbest和全局极值gbest后,通过式(5)和式(6)来更新自己的速度及位置[17]:
vi+1=vi+c1×rand()×(pbesti-xi)+c2×rand()×(gbesti-xi).
(5)
xi+1=xi+vi.
(6)
其中:vi和xi分别为粒子的速度和位置;c1和c2均为学习因子;随机函数rand()为介于(0,1)之间的随机数。
3.2 支持向量机理论
支持向量机(SVM)是当前机器学习领域的一种主流算法,其基于统计学习的理论,通过不断降低置信风险与经验风险,达到最小化结构风险的目的,从而防止过拟合现象的发生[18-19]。相比其他算法,SVM在小样本数据集上有更好的分类结果。其主要思想是寻找使正负类之间分类间隔最大的最优分类面,表示为:
ωx+b=0.
(7)
其中:ω为比例因子;b为常量。
设训练样本为(xi,yi),i=1,2,…,l,求解最优分类面问题表示为:
(8)
其中:l为样本数;ξi为非负松弛变量;C为惩罚参数。通过拉格朗日乘子法可得最优决策函数式:
(9)
其中:ai为拉格朗日系数;K(x·xi)为选择的核函数,自带一个核参数g。
3.3 PSO-SVM识别模型
在Gabor小波变换的基础上将PSO算法与SVM算法有机结合构造PSO-SVM识别模型,其流程如图3所示。初始化SVM中惩罚参数C的取值范围为0.1~20,核函数参数g的取值范围为0.01~20。PSO种群数量为10,迭代次数为50次,学习因子c1=1.5,c2=1.7。之后将特征提取后的544张数据集按4∶1的比例随机划分为训练集和测试集,通过训练数据和PSO算法对参数C和g进行迭代寻优,经过测试后确定最优SVM模型,输出分类结果。
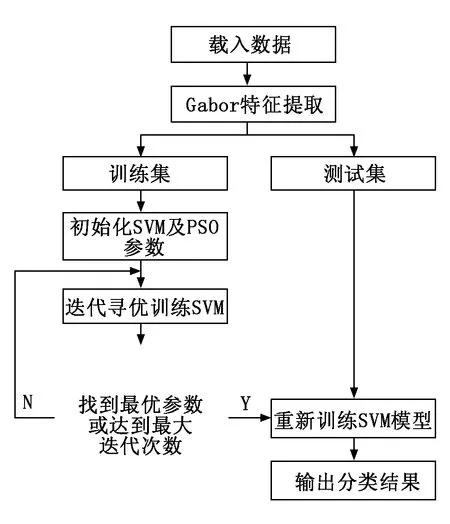
图3 PSO-SVM识别模型流程
4 实验分析
本文采用以上参数设置,使用粒子群优化算法对支持向量机进行优化,从而提高不锈钢焊缝缺陷分类精度。实验结果如图4和图5所示。
从图4可以看出:PSO-SVM算法在迭代20次后便达到最佳适应度,在迭代45次后算法平均适应度便逐渐趋于稳定。
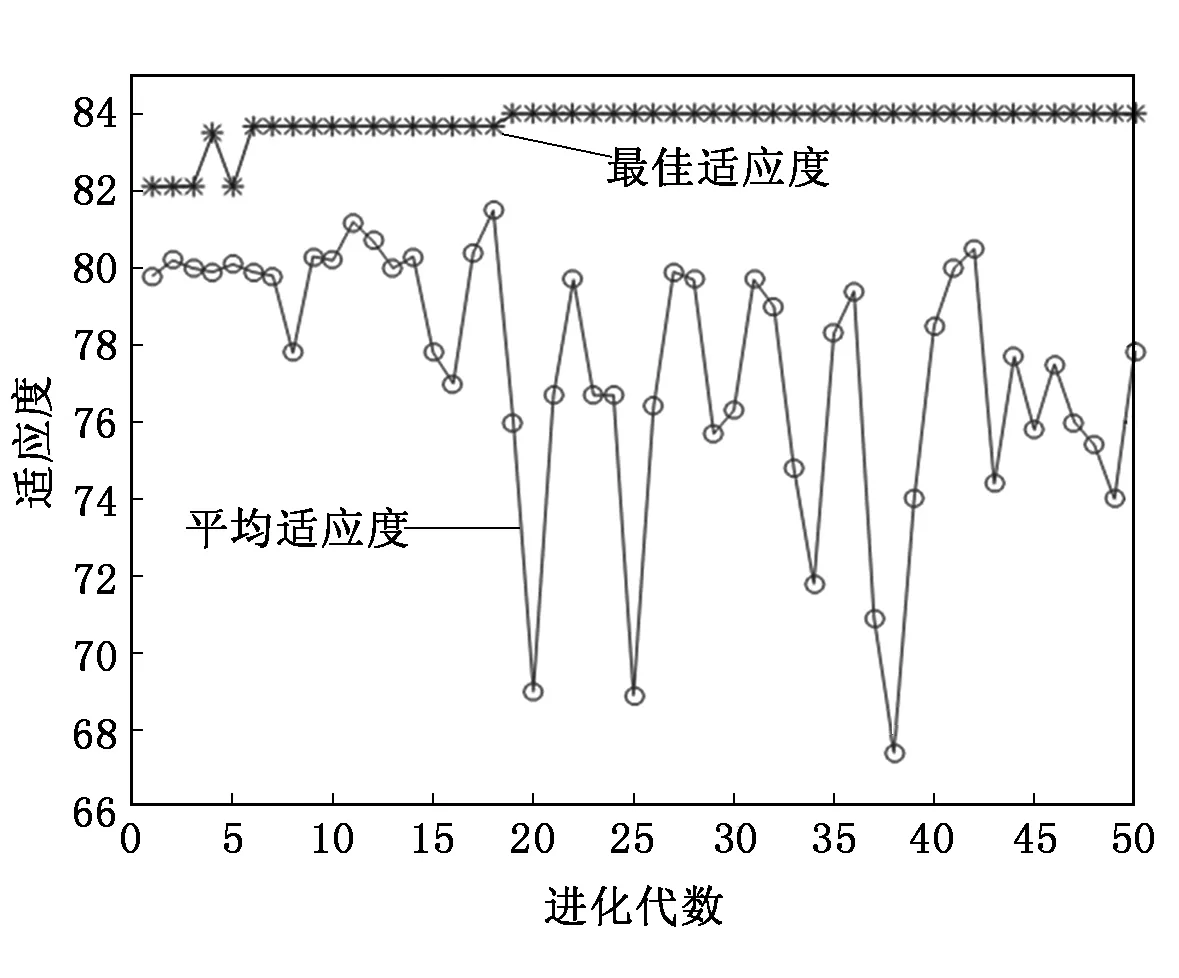
图4 适应度曲线
图5中类别标签1~5分别代表裂纹、气孔、夹渣、未熔合和未焊透五种典型缺陷。
从图5可以看出,本文算法在测试集上表现出了优异的性能,对大多数缺陷类别都能够做出正确的判断,所出现的识别错误主要集中发生在气孔和未熔合这两类缺陷上。发生这种情况可能是本文算法对于分类边界不明显的焊缝缺陷特征提取存在不足,不能够将相似的缺陷特征进行有效的区分。

图5 模型测试结果
采用SVM模型、引力搜索算法优化的SVM模型(GSA-SVM)和本文模型分别对五类不锈钢焊缝缺陷超声样本进行训练和测试,测试结果如表1所示,相比未经过优化的SVM模型和通过引力搜索算法优化的SVM模型,本文模型在训练精度和测试精度上都显示出了良好的效果。相比未经过优化的SVM模型综合精度提高在5%左右,证明本文算法在不锈钢焊缝缺陷超声分类上存在一定的优势。

表1 不同模型识别精度对比
5 结论
本文利用适用于小样本分类的SVM算法以及PSO在参数选择和收敛速度上的优势,建立了基于Gabor小波的PSO-SVM模型用于对不锈钢焊缝缺陷进行分类识别。首先通过Gabor滤波器组对图像数据进行卷积积分,提取焊缝缺陷超声信号的特征,之后借助粒子群算法得到最优SVM模型,实验证明该模型的识别精度优于SVM模型和GSA-SVM模型,可尝试在工程应用中进行推广。
