改进粒子群算法的航空发动机转速系统辨识*

白 杰，刘雨兴

(1.中国民航大学 天津市民用航空器适航与维修重点实验室，天津 300300；2.中国民航大学 航空工程学院，天津 300300)

0 引言

航空发动机作为飞机的重要组成部分，可以将其比作飞机的“心脏”，其本身结构和工作机理非常复杂[1]。从控制的角度来看，航空发动机作为一个复杂系统，对其进行有效控制建立模型是亟待解决的难题。用传统的机理建模方法建立航空发动机数学模型相对困难[2]，目前，闭环系统辨识技术已在航空领域被广泛运用。系统辨识建立数学模型的方法是根据激励被辨识过程得到的响应数据，按照预设的优化准则，通过优化方法计算得到与被辨识过程等价的控制模型[3]。

近年来研究者提出了许多现代智能辨识算法，粒子群辨识算法作为现代辨识方法的主流，在自动控制和闭环系统辨识中得到了广泛的运用[4]。标准粒子群算法中，惯性权重系数为唯一值，惯性权重系数是PSO算法的重要参数。研究发现较大的惯性权重系数可以加快算法的收敛速度，但不容易精确求得解；较小的惯性权重系数有利于局部搜索，可以精准求解全局最优位置和速度，但是算法的收敛精度会降低。因此，目前标准粒子群辨识方法已经达不到工业要求。针对标准粒子群算法的缺点，为了提高粒子群算法全局极值点搜索能力和算法的精准度，需要对粒子群算法惯性权重系数进行改进，为此提出一种(0.4,0.7)均匀分布随机惯性权重的粒子群智能优化算法。本文应用改进的(0.4,0.7)均匀分布随机惯性权重系数粒子群算法对航空发动机转速控制系统进行系统辨识。

1 航空发动机转速控制系统

对于航空发动机转速控制系统，可以近似用如图1所示的结构来表示。

图1中，uk为可测量的外部输入序列，yk为可测量的外部输出序列，εk为白噪声序列，xk为前项通道的输入序列，A(z-1)、B(z-1)为前向通道离散传递函数z-1的多项式，可表示为：

图1 航空发动机转速系统结构

(1)

航空发动机转速控制系统模型方程表示为：

(2)

航空发动机转速系统辨识，即是求解A(z-1)、B(z-1)的参数θ=[a1,a2,...,ana,b1,b2,...,bnb]。由先验条件得到,被控过程A(z-1)的阶数na取2，B(z-1)的阶数nb取1。

2 改进粒子群算法及MATLAB仿真分析

2.1 (0.4,0.7)均匀分布随机惯性权重系数的粒子群算法

粒子群算法中各个粒子都有两种属性，即第i个粒子第j维的位置xij(k)和速度vij(k)；种群也有两个属性，即第i个粒子的第j维的历史最优位置Pij(k)和第j维的全局历史最优位置Gj(k)[5]。

较完整的粒子群算法可用式(3)～式(7)表示[6]：

vij(k+1)=ω·vij(k)+C1r1(Pij-xij(k))+C2r2(Pij-xij(k)).

(3)

xij(k+1)=xij(k)+vij(k).

(4)

(5)

vmax,j=xmax,j+α(xmax,j-xmin,j).

(6)

vmin,j=-vmax,j.

(7)

其中：xmax,j为粒子的最大位置；xmin,j为粒子最小位置；vmax,j为粒子速度的高限值；vmin,j为粒子速度的低限值；α为速度钳制因子；r1、r2为[0,1]之间的随机数；ω为粒子群算法的惯性权重系数，标准粒子群算法中惯性权重系数ω的取值范围为0.4～0.9；C1、C2为学习因子，通常设置为1.9；k为当前迭代次数。

标准粒子群算法中，惯性权重系数为PSO算法的重要参数，惯性权重系数可以作为微粒的大小继承度，惯性权重系数的合理设置能帮助每个粒子迅速找到全局最优速度和位置，所以惯性权重系数的设置是粒子群算法的核心。标准的PSO算法中，较大的ω会有利于全局极值点的搜索，较小的ω可以改善算法的精准度和收敛速度。粒子群智能辨识算法中惯性权重系数ω的设置也十分重要，ω系数设置直接影响着辨识的精准度和收敛速度。本设计采用(0.4,0.7)均匀分布随机惯性权重系数代替标准唯一值惯性权重系数，(0.4,0.7)均匀分布随机惯性权重系数ω表示为：

(8)

其中：kmax为设置的最大迭代次数；ωmax为粒子群算法最大权重系数；ωmin为粒子群算法初始惯性权重系数；r3为[0 1]区间的随机数。

(0.4,0.7)均匀分布随机惯性权重系数可以在算法搜寻后期使粒子跳出个体局部极值，防止算法陷入局部最优，提高全局极值点的搜索能力，也可以改善算法的精准度和收敛速度。改进粒子群算法在系统辨识的操作步骤如下：

(1)根据被辨识过程的动态特性，首先需要确定粒子群模型规模m和设置系统辨识待估参数个数N，初始化粒子群体，随机产生速度和位置。

(2)采用式(3)和式(4)计算更新各粒子的当前速度和当前位置。

(4)对于各粒子，计算当前的适应度值并且与经历过的位置和速度进行比较，若当前速度和位置较好，选取当前的速度和位置作为粒子最好的速度和位置。

(5)对于各粒子，计算当前的适应度值并且与经历过的历史最优位置和速度进行比较，若当前速度和位置较好，选取当前的速度和位置作为粒子历史最优的速度和位置，直到计算出粒子最优速度和位置为止。

(6)判断算法是否满足终止条件，若达到终止条件则算法终止，返回当前最优个体为参数辨识结果；否则返回第(2)步，继续下一循环。

改进惯性权重粒子群算法辨识流程如图2所示。

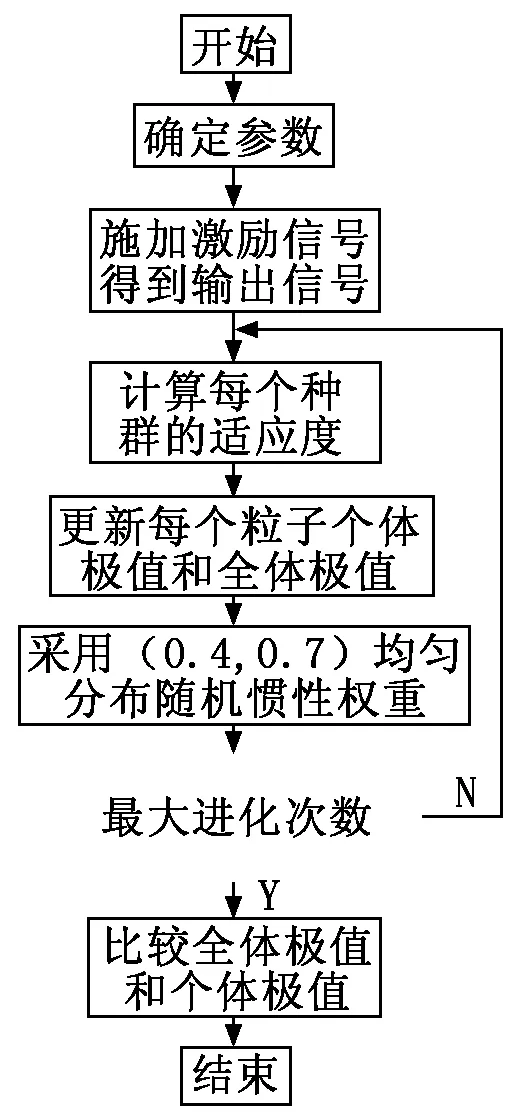
图2 改进惯性权重粒子群算法辨识流程

2.2 改进粒子群算法的航空发动机转速系统辨识仿真分析

本文基于DGEN380发动机虚拟实验平台，以MATLAB为仿真软件，选择4阶M序列作为激励信号，编写4阶M序列程序并导入到DGEN380发动机虚拟实验平台，得到爬升阶段下的燃油流量Wf数据(以序列形式表现)与低压转子转速NL数据(与燃油流量序列一一对应)。以燃油流量Wf(即燃油流量输入序列)为输入，低压转子转速NL为输出，应用改进的(0.4,0.7)均匀分布随机惯性权重系数粒子群算法对航空发动机转速控制系统进行系统辨识。设置待估参数个数N=3，种群规模m=30，探索空间维数j=3，最大迭代次数kmax=200,速度钳制因子α=0.9，ωmax=0.9，ωmin=0.2，C1=1.9，C2=2.0，数据长度L=2 500。改进粒子群算法辨识结果如图3所示，低压转子转速NL的改进粒子群算法模型响应与实际响应的吻合度曲线如图4所示。

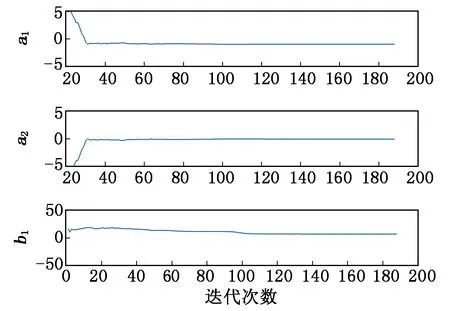
图3 改进粒子群算法参数辨识结果

图4 NL的改进粒子群算法模型响应与实际响应吻合度曲线

为了比较被辨识过程和辨识所得模型之间的特性等价程度，确定被辨识过程和辨识所得模型之间的特性等价，相对最大误差百分数和相对均方差百分数是可以衡量相同激励下被辨识和所辨识得到模型之间响应数据的吻合程度。这两个指标也是实验数据误差分析中十分常见的指标，运用性强，便于接受。在数据采集、模型机构与辨识和辨识算法等方面均无问题，这两个指标是参数辨识准确度检验的重要指标[7]。

相对最大误差百分数计算公式为：

(9)

相对均方差百分数计算公式为：

(10)

根据图4计算可得改进粒子群算法的准确度指标：J1=3.427 6%，J2=2.180 7%。

2.3 标准粒子群算法的航空发动机转速系统辨识仿真分析

选取与2.2节相同的数据，采用标准粒子群算法的惯性权重系数对航空发动机转速控制系统进行系统辨识，辨识结果如图5所示，NL的模型响应与实际响应的吻合度曲线如图6所示。

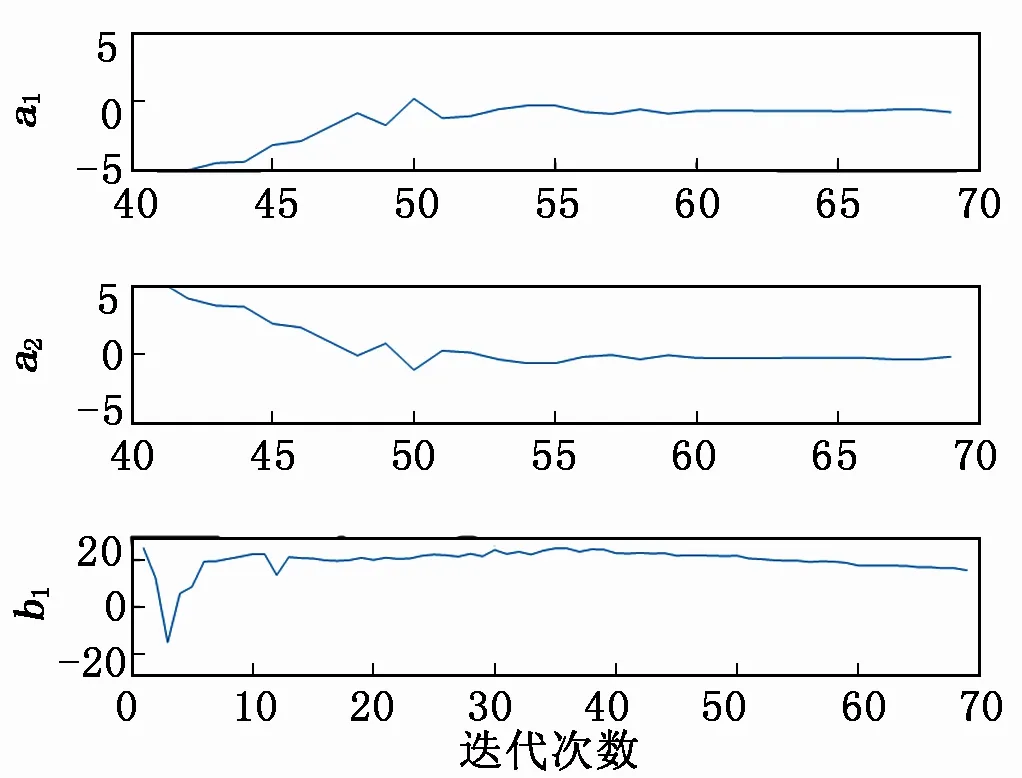
图5 标准粒子群算法参数辨识结果

图6 NL的标准粒子群算法模型响应与实际响应吻合度曲线

根据图6由计算可得标准粒子群算法的准确度指标：J1=7.149 2%，J2=6.203 9%。

2.4 改进PSO算法与标准PSO算法仿真结果比较

由图3与图5可得到标准PSO辨识结果和改进PSO辨识结果，如表1所示。NL的模型响应与实际响应的吻合度可以由相对最大误差百分数J1和相对均方差百分数J2来衡量，标准PSO与改进PSO的J1、J2结果如表2所示。

表1 标准PSO与改进PSO算法辨识结果

表2 标准PSO与改进PSO算法J1、J2结果

比较图3和图5可以得到,(0.4,0.7)均匀分布随机惯性权重系数的粒子群算法比唯一值惯性权重系数粒子群算法有着更快的收敛速度。比较图4和图6可以看出，(0.4,0.7)均匀分布随机惯性权重系数粒子群算法比唯一值惯性权重系数粒子群算法模型响应与实际响应的吻合度更高。综上所述，改进后的粒子群算法相对于标准粒子群算法有着更高的精准度和更快的收敛速度。

3 结论

本文基于DGEN380发动机虚拟实验平台，针对航空发动机闭环转速控制系统，以燃油流量Wf为输入，低压转子转速NL为输出，设计了(0.4,0.7)均匀分布随机惯性权重系数粒子群辨识算法，引用相对最大误差百分数J1和相对均方差百分数J2来衡量相同激励下被辨识和所辨识得到模型之间响应数据的吻合程度。仿真结果表明：改进的(0.4,0.7)均匀分布随机惯性权重系数相比唯一值惯性权重系数，既有利于全局极值点搜索即收敛速度更快，又能提高算法的精准度。