杂质浓度对超声波传播特性及流量测量精度影响的研究

张 蒙 杜广生 程 浩 杨 悦

(山东大学能源与动力工程学院，济南 250061)

我国科学技术水平的快速发展促进了现代装备的自动化、智能化和测量精准水平不断提升。但随着我国节能减排要求的不断提高，急需研发更为精准的热量等计量技术和装备。超声波流量计因其非接触式测量原理、易编程控制、良好的温度和压力适应性、量程比大等优点，常应用于农业灌溉、超临界流体萃取、自动化配料等领域，并在区块链式粮油管控等领域展现了广阔的应用前景[1,2]。

通过测量超声波在介质中顺流和逆流传播的时差，经过计算可得到流体的瞬时流速和流量。在超声波流量计的实际应用中，被测介质常含有一定量的杂质，为提高超声波流量计的测量精度，需要对超声波传播性质和杂质分布特性的进行深入研究。张全兴[3]通过分析声波衰减理论并结合实验和数值模拟，研究了声波在泥浆中的衰减特性并分析了散射衰减、粘滞衰减、热传导衰减之间的关系。李冬等[4]研究了超声波信号对反射表面施加载荷及引起变形的情况，通过求解流体域内Helmholtz方程，得到了固体域的形变，进而分析了测量误差产生的原因。胡博[5]利用超声波的衰减和反射规律提出了一种“面积比值”测量法，并用此方法测量浑水中的泥沙含量。田昌[6]通过ECAH理论模型和“长波长”简化模型，利用两种不同频率的超声波信号，得到了气固两相流颗粒相的平均粒径和浓度，并分析了颗粒物分布的情况。

以上研究主要针对超声波信号的传播特性和内部流场展开，当超声波流量计安装于萃取或供暖管道上使用时，流动介质中含固相颗粒[7,8]。这些杂质会对超声波的传播造成影响，从而影响计量的精度。目前针对这一现象，国内外鲜有此方面的研究。本研究采用理论分析、数值模拟计算和实验研究相结合的方式，研究杂质颗粒浓度在不同流量下对超声波流量计测量精度的影响，本研究对提高超声波流量计的精度和适用性具有一定的参考作用。

1 超声波在两相流介质中的传播特性

针对实际工作环境，超声波的衰减原因主要为扩散衰减和散射衰减。扩散衰减是声传播本身性质决定的，声波传播距离越远，声束面也就越大，但其总声能并未发生变化。散射衰减由供暖水中的颗粒物引起，一些大的颗粒物甚至会完全挡住声波的传播[9]。分析散射声场时，通常把颗粒物当作完全刚性的、半径为r的球体[10]。

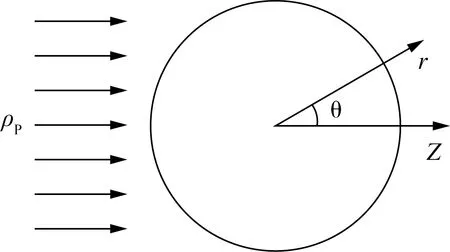
图1 超声波散射传播示意图

设Z方向传播的平面波，入射波用下标p表示，如图1所示，散射波用下标s表示。将入射声压公式以勒让德多项式展开，根据球辐射源声强公式，得到平均散射功率[11]：

(1)

式中：Ip为入射波声强/W/m2。

因此，颗粒物引起的散射衰减，大致可以分三种情况，如图2所示。

图2 不同波长和粒径关系下声波散射状况

当波长远大于粒径时(2πr/λ≪1时)，平均散射功率占平均入射功率比重非常小，与频率和颗粒物半径乘积的四次方成正比，颗粒物的存在对入射波的传播影响较小。当波长与粒径相差较小时，一部分声波会向前继续传播，另一部分的声波会被散射到其他方向。当频率比较高或者颗粒物比较大时(2πr/λ≫1时)，颗粒物将成为良好反射体，完全挡住声波的向前传递。

超声波换能器的工作频率为1 MHz，超声波在水中的传播速度约为1 500 m/s，可计算出超声波波长λ≈1.5 mm。根据防腐技术规程[12]：供水干管上宜设两级过滤器：初级为滤径3 mm的过滤器；二级为滤径0.65～0.75 mm的过滤器，进入流量计前的回水管上应设过滤器，滤网规格不宜小于0.25 mm(60目)。

结合实际情况，本研究选取粒径为0.2 mm的杂质颗粒进行研究，成分采用CaCO3[13]。计算得出2πr/λ=0.42，经过滤后颗粒杂质的存在仍然会造成声波衰减，从而影响测量的准确性。

2 杂质浓度分布的数值模拟计算

2.1 数学模型

对于含杂质水中的工作情况，液相采用标准k-ε模型[14]：

湍流动能k方程：

(2)

湍流耗散ε方程：

(3)

式中：k为湍流动能/J；ε为湍流耗散率/%；ρ为流体密度/kg/m3；t为时间/s；ui为相应方向上的速度分量/m/s；Eij代表应变率；μt代表湍流黏度/Pa·S;方程组中所引入的常系数C1ε、C2ε、Cμ及σK，σε的值分别为：C1ε=1.44，C2ε=1.92，Cμ=0.09，σk=1.0，σε=1.3。

固相的影响在方程中以外部作用力的形式表现。因此做出如下假设：

1)液相和固相均具不可压缩性；

2)速度与浓度分布已达到稳定状态，符合均匀流条件；

3)液相运动粘滞系数与纯液相一致；

4)当浓度较小时，认为是自由沉降，当浓度达到一定程度之后，颗粒的相互干扰渐趋严重，沉速公式考虑浓度的影响[15]；

5)颗粒物看作刚性小球，认为颗粒物主要成分为碳酸钙。

基于以上假设，为了更精确的考虑颗粒物之间的相互作用，采用Fluent多相流模型中的Eulerian模型[16,17]。

(4)

式中：ps为固体压力/Pa；αs为固相体积分数/%；Ts为固相间的剪切力张量；Fs为固相外部体积力/N；Flift,s为固相升力/N；Fvm,s为固相质量力/N；Kls为液相与固相间的动量交换系数/%；mls为液固两相的质量转递系数/%。

2.2 物理模型建立

以一款DN25型基表模型为基础，为消除边界条件对计算的影响，在表前和表后取10倍管径的直管段，结构如图3所示。L为表长，L=110 mm，D为口径，D=25 mm，l为缩颈长度，l=10 mm，d为测量段管径，d=16，θ为换能器夹角，θ=10°。采用结构化网格，并在基表位置和边界层处进行了网格加密，并通过试算确定网格无关性，实际计算网格数量为383万。

图3 DN25 型基表结构示意图

2.3 边界条件设定

根据检定规程，入口边界条件取计量标准规定的五种流量点，包括：0.07、0.14、0.35、1.05、3.5 m3/h，出口边界条件为压力出口，管壁为无滑移边界，重力沿垂直方向加载(图4中Y轴负方向)。取流道中间位置的截面作为观察面。

2.4 不同平均浓度杂质的分布规律

考虑到超声波换能器的声波辐射面宽度为10 mm，图4中黑色横线杂质浓度的线平均值作为该高度处的杂质浓度。垂直方向同间隔共取200个数据。杂质平均体积分数为0.15%、0.5%和5%，不同流量下垂直方向上杂志体积分数分布，如图5～图7所示。

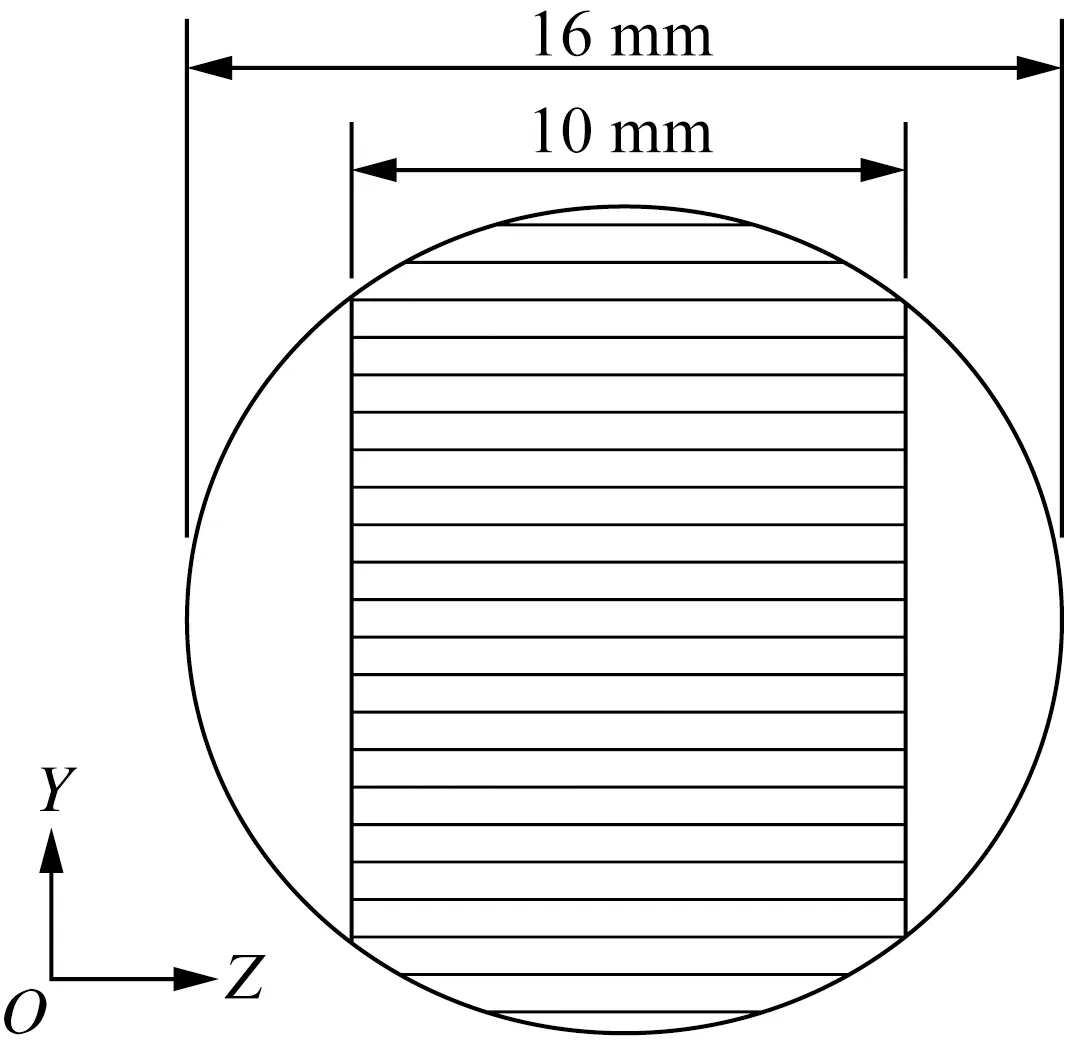
图4 杂质分布观测截面示意图

在图5～图7中，-8～8 mm对应流道截面的底部到顶部范围，超声波换能器的辐射范围为-5～5 mm，定义为中心区域。随着体积分数的增大，不同流量点的杂质分布体积分数增大；随着流量的增大，流速提高，湍流强度增强，流体携带杂质的能力增大，杂质分布逐步向中心区域扩展，对声波的传播产生影响。

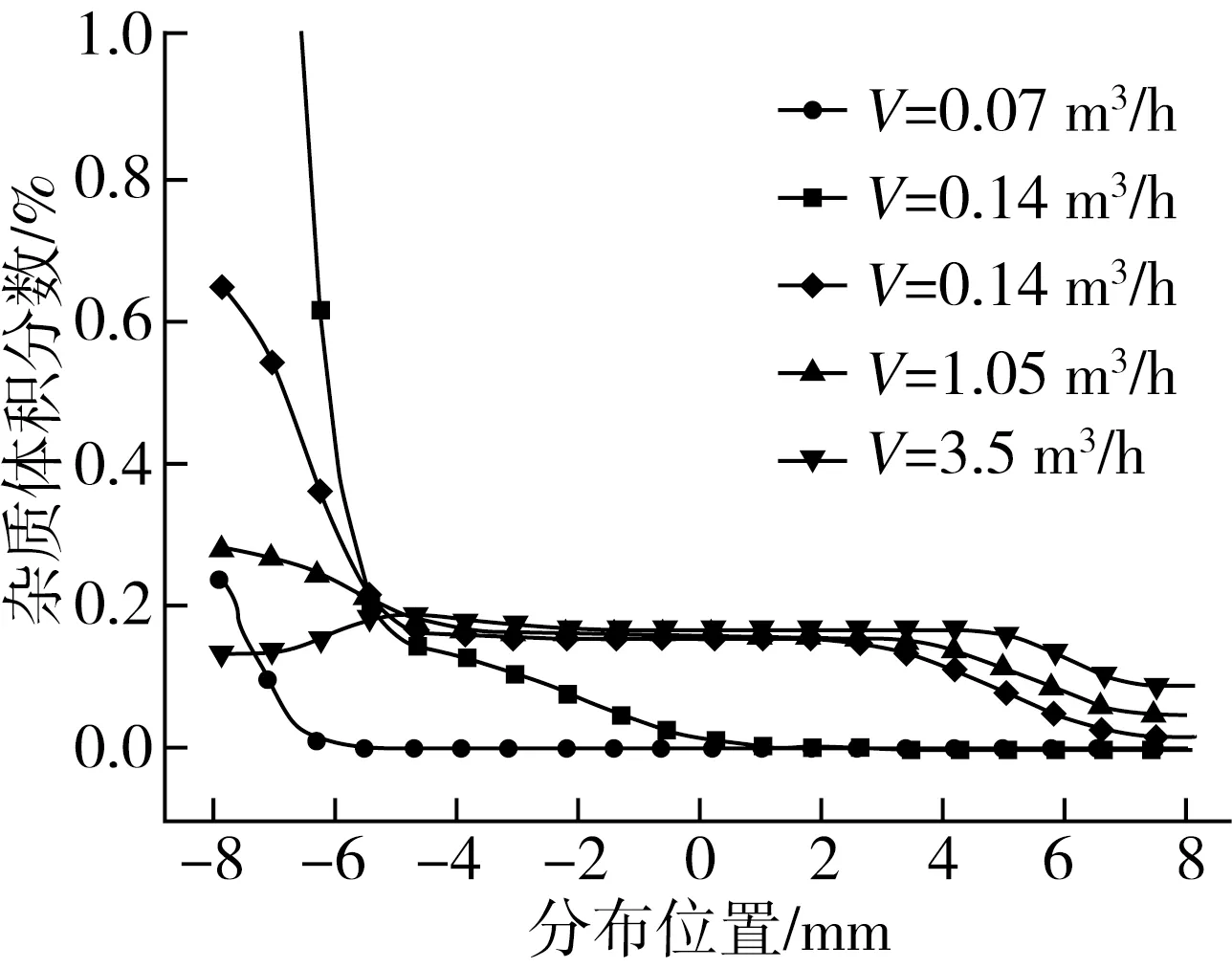
图5 平均体积分数为0.15%纵向中心的杂质分布

图6 平均体积分数为0.5%纵向中心的杂质分布

图7 平均体积分数为5%纵向中心的杂质分布

在小流量0.07 m3/h的工况下，杂质基本沉积在底部区域，随着体积分数的增大，底部沉积区域增大，当体积分数为5%时，杂质分布范围最大，但所有体积分数条件下的颗粒分布均未到达中心区域，对声波的传播没有影响；当流量为0.14 m3/h时候，不同体积分数情况下分布基本一致，大部分颗粒沉积在-8～-5 mm区域，在-5～0 mm的区域逐渐减小，之后趋近零；当流量为0.35 m3/h时，在体积分数为0.15%的工况下，杂质的中心区域分布基本水平，随着体积分数的增大，分布开始产生变化，逐步向低于中心区域的方向发展，即该流量为杂质体积分数分布产生变化的分界点；当流量为1.05 m3/h和3.5 m3/h时，杂质在中心区域基本呈水平分布，对误差的影响基本一致。

图8～图10为0.07、0.35、3.5 m3/h流量下，流道截面不同体积分数的杂质分布云图。杂质的体积分数从蓝色到红色逐渐增加。

图8 0.07 m3/h流量工况下杂质的浓度分布图

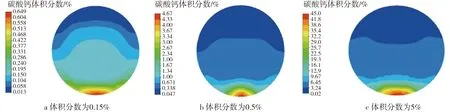
图9 0.35 m3/h流量工况下杂质的浓度分布图

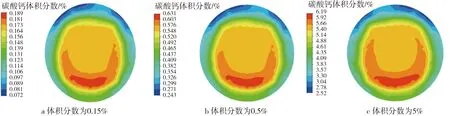
图10 3.5 m3/h流量工况下杂质的浓度分布图

如图8所示，在小流量工况下，受重力作用影响杂质沉积在底部，在中心区域分布趋近零，对声波的传播没有影响；图9中0.35 m3/h的流量工况下，平均体积分数越低，杂质在中心区域分布的范围越大，随着平均体积分数的增大，杂质向管段下方区域分布，且分布区域的杂质体积分数增大，对声波传播产生的影响逐渐增大；在流量较大时，如图10所示，流道内呈紊流流动状态，流体质点在纵向运动的同时也带动了固相颗粒在纵向上运动，因此杂质分布比较均匀，涵盖了整个中心区域，并且流速越大，体积分数分布会越均匀，此时超声波传播路径上的杂质体积分数等于平均体积分数。

3 含杂质水流对超声波精度影响实验

3.1 实验方法

根据上述数值分析获得的结论，通过实验研究获得杂质对检测精度的影响。分别在清水、加碳酸钙的颗粒两相流中进行流量测量，与标准流量计数值对比，进行误差分析。实验表为DN25 型，精度等级为2级。流量检定实验台的误差精度为0.1%，可选用标准表法和称重法进行检定。

根据计量检定规程和数值模拟计算结果，本实验研究测量的流量点分别为0.07、0.14、0.35、1.05、3.5 m3/h。经过颗粒物筛选，碳酸钙颗粒密度为2.7 g/cm3，采用的碳酸钙粒径为0.2 mm。实验中，碳酸钙颗粒物的体积分数分别为0.15%、0.5%、5%。在水箱中进行均匀混合后达到上述要求的平均体积分数，再对检测精度进行测试。

误差计算公式为：

(5)

式中：q1为被检表测量的流量值；q为实验台测量的标准值，本研究采用的实验方案为称重法，通过标准秤测量流过的流体质量，进而计算流量q。

3.2 结果与分析

不同流量点测量值的相对误差随颗粒物体积分数变化曲线如图11所示。

图11 误差随碳酸钙浓度的变化曲线图

纯水工况下，超声波流量计在不同流量点下测量的误差变化小于1%；随着体积分数的增大，含杂质水的流量检测误差逐渐增大，且随着体积分数的增大而增大。在小流量0.07 m3/h时，误差不受影响，0.14 m3/h下不同体积分数的杂质误差开始增大，0.35 m3/h为曲线变化分界点，在此流量点之后，不同颗粒浓度的测量误差开始逐渐趋于水平。该误差规律与上述数值模拟计算分析一致，验证了本研究数值计算的正确性。由于杂质的存在，增大了超声波的衰减，由于信号的衰减导致换能器接收信号时间推迟，会引起的时差增大。

时差计算公式为：

(6)

式中：c为超声波在介质中的传播速度，L为流动方向上的传播距离，vl为被测流体的线平均流速。由于杂质存在使声波产生衰减，使得换能器表面接收声波时较晚到达监测值，时差变大，产生正向误差。杂质浓度越大，在中心区域分布越多，产生的误差越大。

4 结论

本研究通过理论分析、数值计算和实验研究相结合的方法，分析了杂质浓度对超声波传播特性及流量测量精度的影响，主要结论如下：

由圆球辐射场的声能公式推导及散射衰减规律的研究，分析获得了粒径对声波的影响，进而分析杂质会引起声波的衰减，影响测量的准确性。

通过两相流的数值模拟计算，获得粒径为0.2 mm的杂质在不同平均浓度工况下，纵向截面中心位置的线平均浓度分布规律。即小流量沉积在底部，远离声波传播的中心区域，不会对声波传播产生影响；随着流量的增大及浓度的增大，杂质分布逐渐靠近中心区域，对声波传播产生的影响逐渐增大；当流量达到一定值，杂质分布涵盖整个中心区域，超声波传播路径上的杂质体积分数等于平均体积分数，对声波传播影响最大。

通过对超声波流量计在纯水、含不同浓度杂质水中的误差分析，明确了误差分布规律，并通过对声波信号的分析，阐明了杂质对测量误差影响的机理。