基于高频天平测力试验的广播电视塔等效静力风荷载研究

朱悦 严亚林 邱晖

(1.中广电广播电影电视设计研究院 北京100045；2.中国建筑科学研究院 北京100013)

引言

电视发射塔属于高耸建筑，由于其结构体系较柔，因此对风荷载敏感，国内外针对该类结构体系的风致响应已经展开了一定的研究[1～5]。研究方法主要有两类，一种方法是采用测力天平试验获得建筑底部的基底倾覆力及倾覆弯矩响应，结合结构本身的动力特性及结构振型的假定计算结构风致响应，代表性建筑是广州新电视塔，周暄毅[6]等利用截断模型的天平试验获得了非定常气动力后计算了电视塔结构的顶点位移、加速度等响应；另一种方法是直接通过气动弹性模型风洞试验测量塔体反应，代表性建筑为东方明珠广播电视塔，顾明[7]等通过全塔气动弹性模型风洞试验获得了电视塔的加速度、风振系数及位移等结果。对于量大面广的电视塔类建筑而言，采用气动弹性模型进行研究的成本较高，因此一般工程上借助于刚性模型高频天平测力试验来获取结构所需的设计风荷载。

采用刚性模型测力天平试验一般可以获得结构底部剪力和弯矩响应，而对于结构荷载的分布形式难以确定，采用基底弯矩和一阶振型假定所获得的平均风荷载分布难以反算出准确的平均基底剪力。对于外框结构，还存在外框和内筒风荷载的分配问题。

1 高频天平测力试验原理

1.1 力学模型

电视塔建筑一般为轴对称建筑，相对于平动位移其风致竖向位移及扭转响应可以忽略，因此构建结构模型时，可仅考虑结构平动响应。

在风荷载作用下的运动方程可由式(1)表示:

式中，M、C、K分别为结构质量、阻尼和刚度矩阵；F为风荷载。x为结构层或节点在x、y方向的平动。

对位移进行模态分解，有:

式中:φj为结构第j阶振型向量；ξj(t)为第j阶广义坐标。将式(2)代入运动方程并左乘，得出解耦后的广义坐标的运动方程:

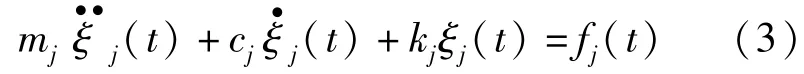
式中:mj为广义质量；cj为广义阻尼；kj为广义刚度；fj为广义力。

假定x、y向振型均为线性振型，广义力可表示为:

式中:Mx(t)、My(t)分别为建筑基底x和y方向的弯矩；Cjx、Cjy分别为x、y向振型参与因子，当振型参与时取值为1，当振型不参与时取值为0，对于振型不耦合的建筑物，广义力中仅包含其中一项而另外两项为零；H为建筑总高度。

1.2 风致响应和等效静力风荷载的计算

由于Mx(t)、My(t)均已经由天平测量得到，因此可对解耦后的广义坐标的运动方程式(4)求解。求解在频域进行，在求取脉动响应时，应利用中心化之后的广义力进行计算。

位移响应的均方根和均方加速度分别为:

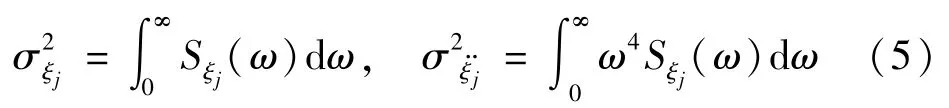
式中:σξj为对应广义位移ξj的均方根；Sξj(ω)为对应ξj的功率谱；ω为圆频率；σξ··j为对应广义加速度的均方根。在小阻尼(＜5%)前提下，位移响应可进一步简化为:

式中:σfj为对应第j阶广义力的均方根；Sfj(ω)为对应第j阶广义力的功率谱；ζ为结构阻尼比；ωj为结构第j阶自振圆频率。

仅考虑前两阶振型，且对于固有频率稀疏的小阻尼结构而言，振型交叉项可忽略，因此结构最高点总的均方位移可根据平方和开平方(SRSS)的振型组合公式得出:

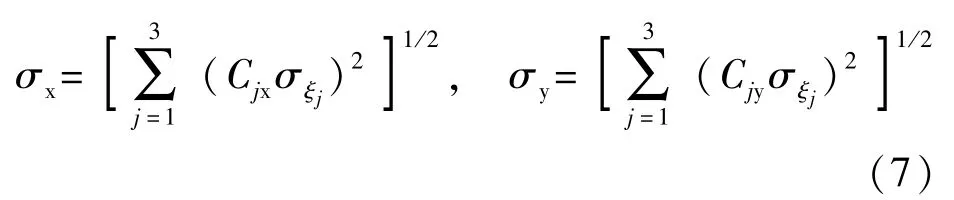
平均风振响应同样可根据振型分解方法求出:

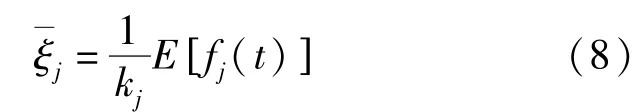
式中:E表示数学期望。

求出风致响应平均值和脉动值后，根据结构的一阶振动假定，并且不考虑不同方向的耦合，则沿高度分布的等效静力风荷载[3]可按照式(9)计算，式中第一部分为平均风荷载，第二部分由脉动响应均方根反算获得，可称为“等效动力风荷载”。

式中:Feq为等效静力风荷载；ω为结构自振圆频率；l代表x、y两个方向。式(9)表示l方向等效静力风荷载为该方向一阶位移响应与刚度的乘积。

1.3 振型修正

式(4)的计算基于建筑的振动模态为理想化的直线形状，因此基底弯矩与广义气动力的对应关系相对简单，可以把基底弯矩响应功率谱直接用于结构响应计算。但是，当建筑的振型与理想的直线形状差别较大时，这种简单的处理将使计算结果和实际响应之间产生一定的误差。对于这种情况，可以对基底弯矩谱进行振型修正，得到精度较高的广义气动力谱后，再用于结构响应计算。

Xu Y.L.et al[8]基于风荷载沿高度完全相关的假定，建议利用振型修正因子对广义力计算式(4)进行修正，即:式中:ηa为顺风向振型修正因子；α为风剖面指数因子；β为结构振型指数因子。

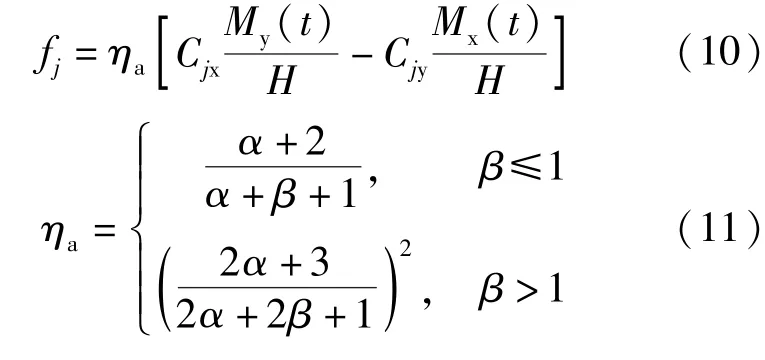
2 对等效静力风荷载的讨论

由于仅考虑结构的一阶振动，因此式(9)中第2项即能够准确反映结构的一阶等效风振力；但结构由于天平试验准确获得了建筑底部的基底剪力和基底弯矩平均值，采用式(9)中第1项方法计算却不一定能够反算出测试的基底剪力和基底弯矩，即式(9)第一项的计算结果与式(4)中作为输入条件的Mx、My有可能不一致。造成这一现象的原因在于式(9)采用了结构一阶振型作为平均荷载的分布形式，这与平均荷载的实际分布形式存在差异，因此需要对平均风荷载的分布形式进行讨论。

另一方面，对于电视塔外框内筒形式的电视塔结构，其内外两部分的等效风荷载分配比例也是值得关注的问题之一。

2.1 等效静力风荷载的平均风荷载分布

基底弯矩与基底剪力是测力天平试验中获得的主要试验数据，因此在假定荷载分布时，至少应保证平均基底弯矩与平均基底剪力的准确性。

式(9)中平均风荷载为结构平均位移反算的风荷载，通过该式计算的结构平均基底弯矩和剪力与实测数据的比值为式(12)、式(13)。

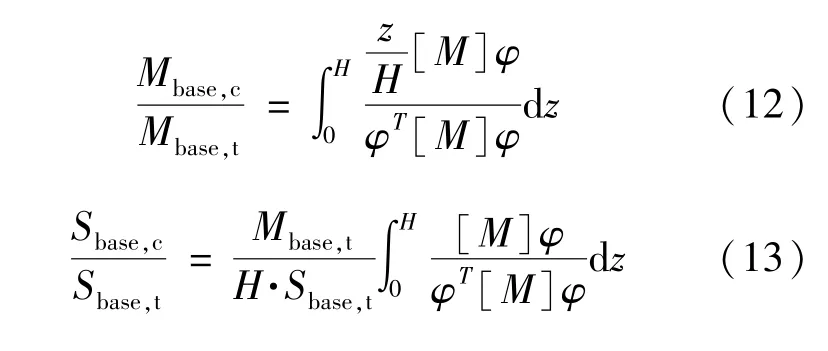
式中:下标c表示计算值，t表示试验值。

式(12)表明，只有当结构振型为严格的线性振型，通过平均响应反算的基底弯矩才有可能与实测基底弯矩平均值相等；由于实际振型与线性振型一般存在一定的差异，因此当荷载分布能够反算出准确的基底弯矩时，结构的平均位移响应计算值与实际值一般会存在误差。

式(13)等式右侧第1项表示实测结构风荷载合力作用点的相对高度，第2项为与结构质量、振型相关的系数；基于等效静力风荷载的基底剪力反算值与实测值的比值很大程度上取决于实测数据，由于实际结构受风的复杂性，因此很难保证计算结果与实际结果一致。

因此采用式(9)第1项计算假定结构沿高度分布的荷载(通过振型体现)存在不确定性。

计算平均风荷载直接的方式是采用《建筑结构荷载规范》(GB50009—2012)平均风荷载的计算方法，即:

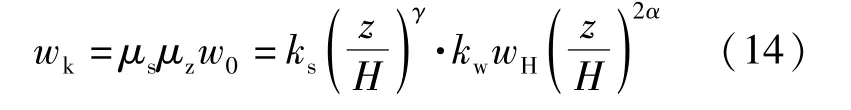
通过求解式(15)的弯矩方程和式(16)的剪力方程便可确定ks、γ的取值，并使结构计算的基底响应与试验的基底响应值相等。

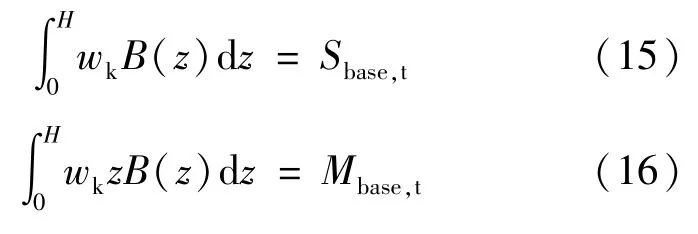
2.2 内外等效静力风荷载的分配

由式(9)可知，等效静力风荷载与结构质量及振型有关，因此对于内外结构，其风荷载分布情况只需通过内外区域的质量、振型进行分配即可获得较为准确的结果。

若通过式(14)～式(16)计算结构平均风荷载，则需要通过区分内外结构的体型系数及两部分结构的挡风面积进行分配。将内外结构分割，分别进行天平测力试验，便可获得两部分平均风荷载；而内外结构只进行一次试验条件下，假定内外结构沿高度体型系数完全一致，则仅需根据内外结构挡风面积即可确定各部分的平均风荷载分配。

3 工程实例

3.1 项目概况

六安电视塔总建筑高度308m，其中天线桅杆段高91m；总建筑规模为5000m2，其中塔座部分建筑面积3500m2，塔楼部分建筑面积1500m2。为广播电视信号发射、信号接收、城市应急指挥、文化景观等多功能于一体的文化建筑景观塔。该塔采用空间格构式筒体结构，如图1所示。

3.2 风洞试验

根据风洞阻塞度要求、转盘尺寸及原型尺寸，试验模型缩尺比确定为1∶300。为保证测力试验结果的准确性，模型内侧采用铝合金材料，外侧采用ABS材料，保证模型较轻，但刚度较大。试验在中国建筑研究院风洞实验室的4m×3m(宽×高)试验段进行，试验风速为10m/s，天平-模型系统的基阶频率为30Hz，在保证结构与模型的Strouhal数一致时，换算到结构原型约为结构基阶频率的2.5倍。风洞试验情况见图2。由于电视塔外形完全对称，因此分析时只考虑一个风向角来流作用。图3为基底弯矩测试值。

图1 六安电视塔结构及尺寸Fig.1 Structural configuration of Lu an TV tower

图2 六安电视塔风洞试验Fig.2 Wind tunnel test of Lu an TV tower

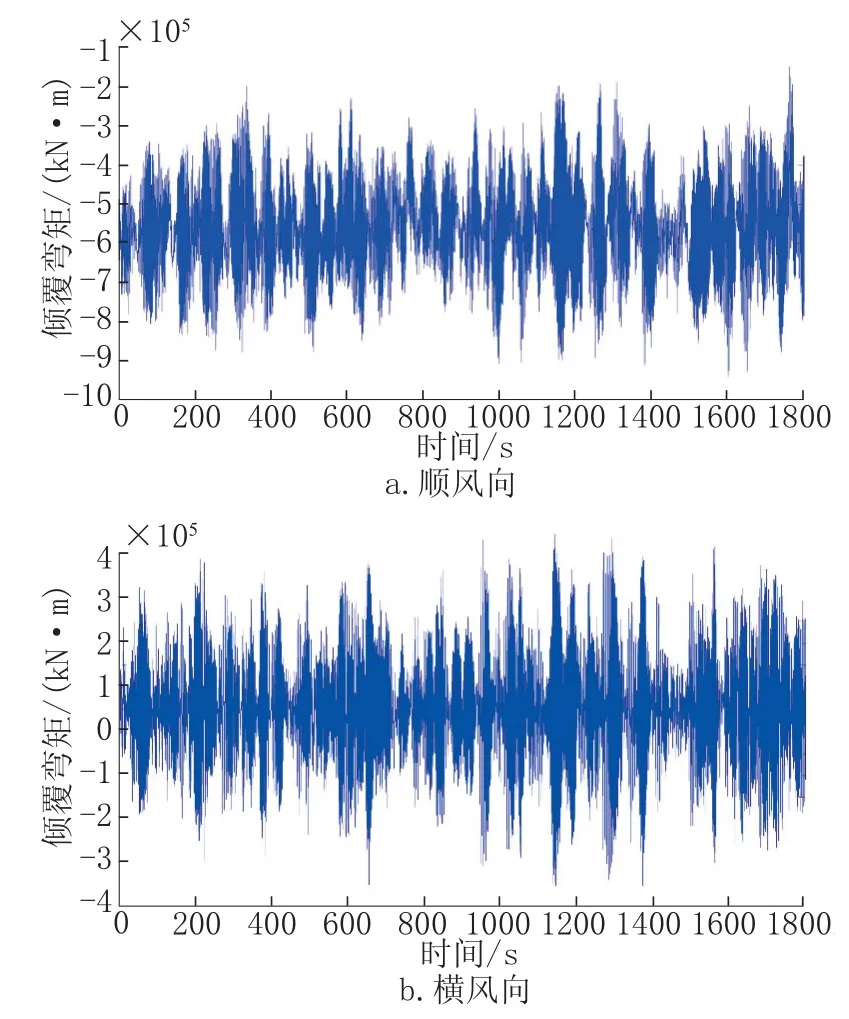
图3 高频测力天平测量的风荷载时程Fig.3 Wind loads tested by high frequency balance

3.3 计算参数

风荷载计算参数按照相关规范 选 用[9，10]，地貌类别为B类，基本风压为0.4kPa。结构一阶自振频率为0.159Hz，二 阶 频率为0.1592Hz，结构阻尼比为0.015。结构模型共有74层，其中1～32层为上人高度层，33～74层为天线层。图4、图5分别为各楼层结构质量及沿高度分布的振型情况；图5对振型进行指数拟合，振型指数为1.8。

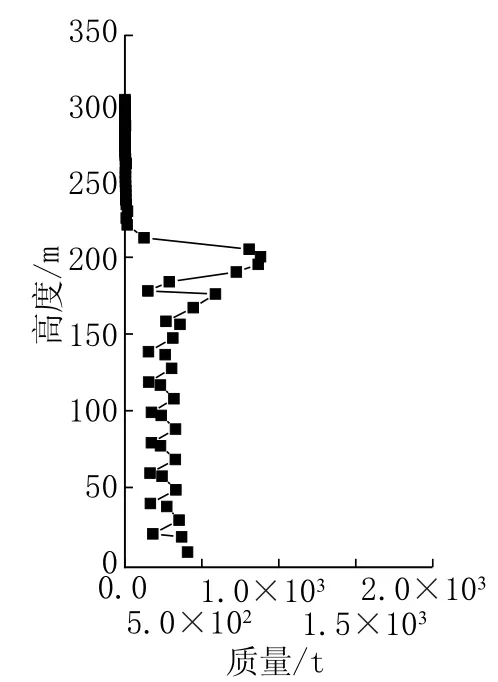
图4 六安电视塔分层质量Fig.4 Floor mass of Lu an TV tower

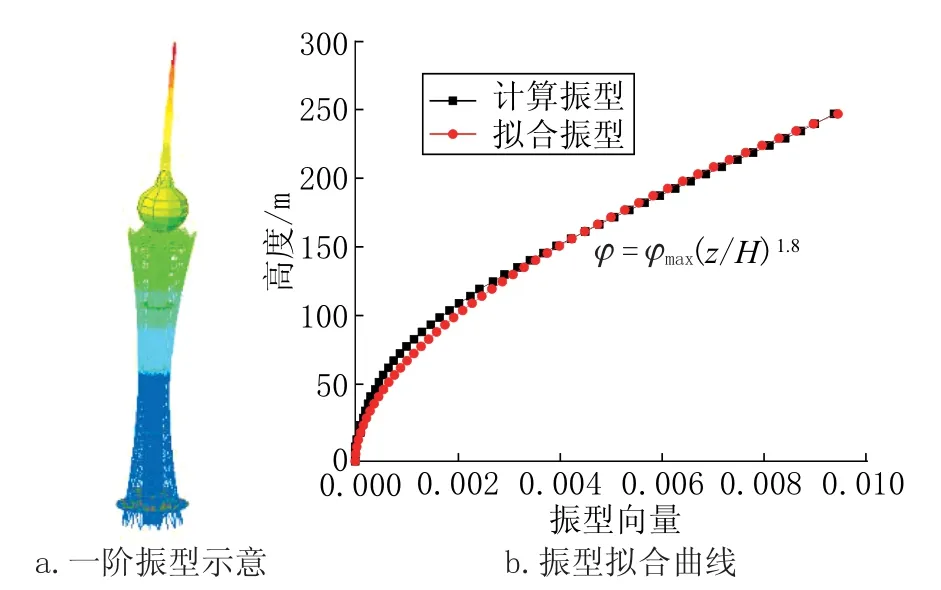
图5 六安电视塔振型及其拟合Fig.5 Mode shape and fitting of Lu an TV tower

3.4 计算结果

图6～图8分别为等效静力风荷载、剪力、弯矩结果。由图6可知，在建筑底部(30m以下)和建筑受风面积较大位置(197m～205m)，结构等效静力风荷载差异较大；在较高位置(197m～205m)较大受风面上的等效风荷载采用振型等效计算结果更大，而电视塔底部等效风荷载则是采用体型系数计算的结果更大。从平均风荷载角度来说，电视塔底部具有较大的迎风面，采用体型系数计算给出的结果更为合理。

图7给出各层剪力，两种形式荷载分布对应的建筑底部的总剪力相差在1%以内；电视塔30m～150m高度范围，剪力误差在5%以上；150m以上位置两种形式风荷载对应剪力误差在3%以内。图8为各层倾覆弯矩，其中采用体型系数计算的基底倾覆弯矩为实测基底弯矩，从图中可以看出，由于结构振型偏离直线振型较多，结构基底弯矩会产生较大的误差(＞5%)。因此为了获得较为准确的风荷载分布数据，采用测力试验数据时应考虑振型修正。

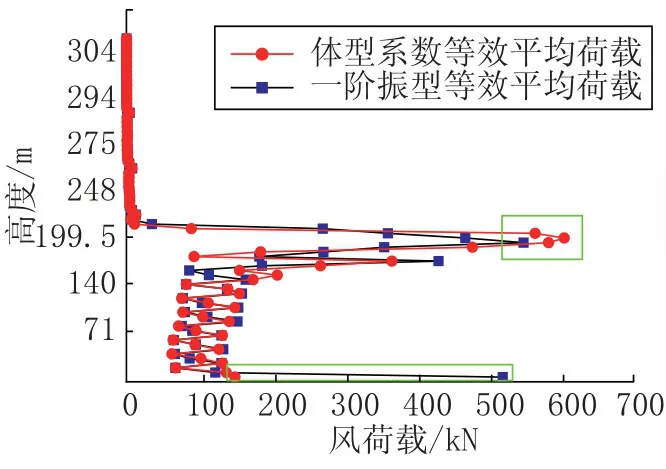
图6 六安电视塔等效静力风荷载Fig.6 ESWL of Lu an TV tower

图7 六安电视塔剪力Fig.7 Shear force of Lu an TV tower

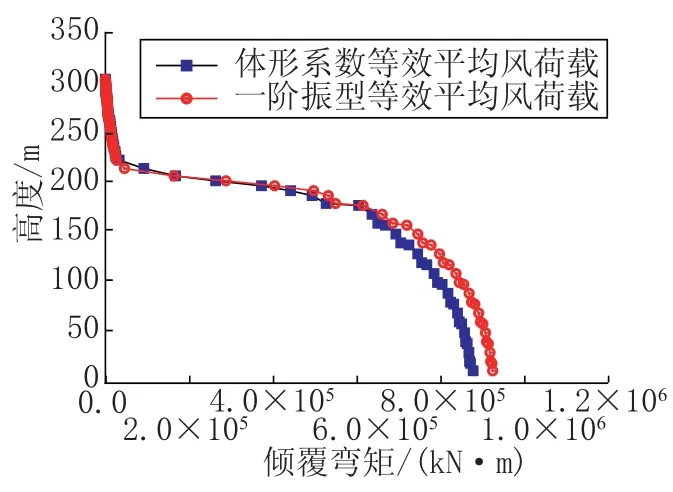
图8 六安电视塔倾覆弯矩Fig.8 Overturning moment for Lu an TV tower

图9给出该电视塔内外等效静力风荷载分配情况，其中有框架部分为30m～200m，在此范围内，假定内外结构受风体型系数相等，则外框结构风荷载占总层风荷载的30%～40%。

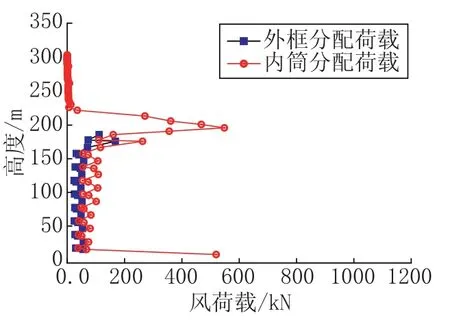
图9 六安电视塔等效静力分配Fig.9 ESWL distribution for Lu an TV tower

5 结论

1.基于天平试验并不能直接获得结构平均荷载分布，采用一阶振型计算结构平均风荷载可能存在误差；假定结构体型系数沿高度指数分布，可以保证结构基底弯矩与基底剪力实测值与基于等效静力风荷载的反算值一致。

2.对于六安电视塔项目，采用一阶振型与沿高度指数分布体型系数计算的基底剪力相差不大，但层荷载分布和电视塔底部倾覆弯矩存在5%以上的误差；该项目外框分担约35%的层风荷载。