考虑螺栓滑移的输电塔结构内力分析∗

胡剑 张贵祥 刘红军 李正良

(1.重庆大学土木工程学院 400045；2.重庆瑜煌电力设备制造有限公司 402160)

引言

目前的螺栓滑移研究中，大多只针对螺栓沿杆件轴线方向滑移的情况。但对于K型节点来说，在支角钢杆端弯矩作用下，该节点会产生转动，当荷载足够大时，便会产生螺栓绕节点的转动滑移，此转动滑移对于输电塔结构内力有无影响或其影响大小尚有待研究。

早期就有学者提出了螺栓滑移模型的数学表达式，如理想连接滑移模型、线性模型、多项式模型以及指数模型等[1，2]。江文强等[3]对构造节点进行了精细模拟。杨风利等[4，5]进行了螺栓连接拉伸试验及有限元仿真，分析了一些参数对于螺栓节点荷载-变形曲线的影响规律。王朋、高康等[6]进行了螺栓滑移对格构式结构静动态特性的影响研究。徐建设、陈以一等[7]总结得出了螺栓孔壁变形和总滑移量的发展规律，并据此给出了螺栓孔壁变形和连接滑移量的计算公式。舒前进等[8]提出了角钢中螺栓连接节点滑移变形的简化四阶段线性力学模型。

研究者通常在有限元中采用非线性弹簧单元(combin39)模拟有螺栓滑移的连接节点，但弹簧单元一般只能模拟梁杆单元沿轴线方向的滑移变形，不能同时考虑因杆端弯矩而产生转动滑移的影响。因此本文首先对K型节点的转动滑移性能进行研究，然后建立塔身模型，利用ABAQUS中的连接器(Connector)模拟螺栓连接节点，该连接器可同时定义沿杆件的轴向滑移与绕节点的转动滑移行为。

1 螺栓滑移过程

由Ungkurapinan[2]提出的螺栓滑移荷载位移曲线模型如图1所示，整个过程可以分为4个阶段。

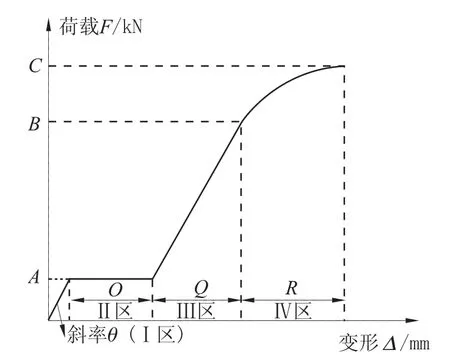
图1 滑移曲线Fig.1 Slippage curve

第①阶段:摩擦受力阶段，如图2a所示，由于螺栓预紧力的作用，荷载靠摩擦力传递，故最初节点处于弹性工作状态，如图1中I区所示，此时滑移量为Aθ；此过程中螺栓杆与孔壁之间的间隙略微减小。

第②阶段:间隙滑移阶段，当荷载超过最大静摩擦力A后，栓杆与孔壁间的间隙消除，如图2b所示，在图1当中处于II区状态，此时间隙滑移量为O。

第③阶段:栓杆传力阶段，此时依靠栓杆与孔壁挤压传递荷载，如图2c所示。在图1的荷载位移曲线中处于III区状态，滑移量为Q；当荷载为B时，达到弹性极限。

第④阶段:弹塑性阶段，即图1中的IV区，此时变形主要由孔壁及栓杆的弹塑性变形引起，如图2d所示，此阶段滑移量为R。

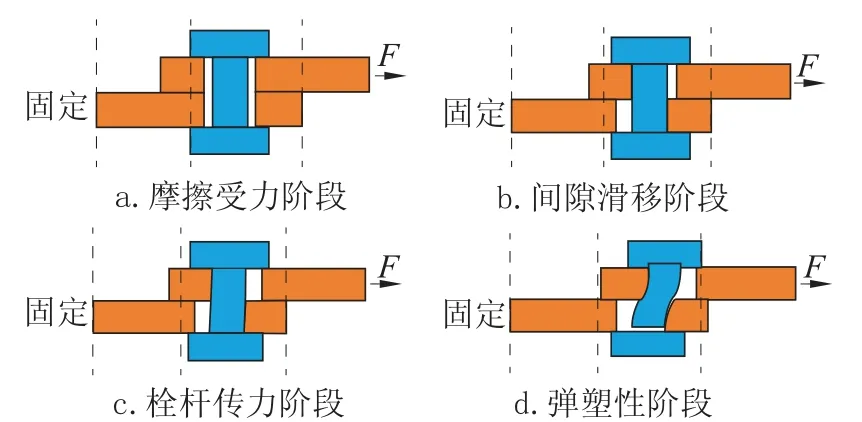
图2 螺栓滑移的四个阶段Fig.2 Four stages of bolt slippage

2 K型节点转动滑移分析

以往的输电塔螺栓滑移研究中，均只对沿杆件轴线方向的滑移进行分析探讨，但除此之外，在类似K型等节点中也存在着转动滑移，这种滑移对节点刚度的影响不可忽略。本节运用ABAQUS6.14建立与重庆大学赵楠博士论文[9]中K型节点试验相对应的有限元模型，主要研究螺栓强度与主角钢螺栓个数对转动滑移的影响，试验构件主要参数见表1。

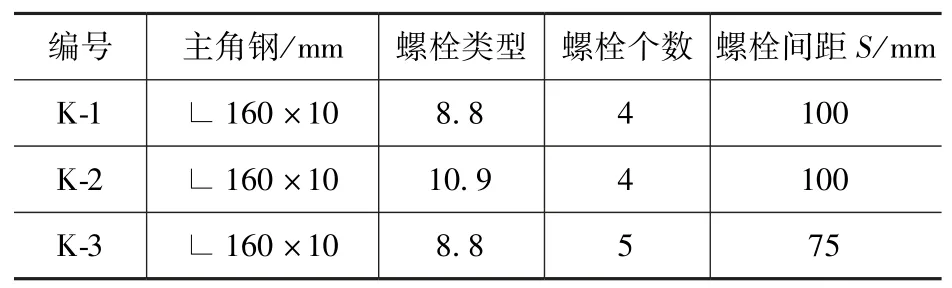
表1 试验构件尺寸Tab.1 The size of test components

2.1 有限元模型

模型中所有构件均采用线性六面体缩减积分单元C3D8R建模，螺栓直径d=20mm，孔径D=21.5mm，节点板示意及边界条件如图3所示。主角钢一端固定，另一端仅释放沿轴线方向的位移，支角钢仅释放沿力F方向的轴向位移。钢材采用线性硬化模型，泊松比u=0.3，屈服强度与强度极限根据文献[9]中给出的材性试验结果取得，弹性模量取E=210GPa，接触面法向设置为硬接触，切向为罚函数，摩擦系数为0.3。有限元模型如图4所示，不降低精确度的情况下，为提高计算效率，只在螺栓及螺孔附近设置细致网格，其他次要部分网格划分略粗；螺栓预紧力根据《钢结构设计标准》(GB 50017—2017)[10]第11.4.2条规定，取N=0.6075σA=95.178kN，支角钢上力F的加载方式为一拉一压同步加载，并采用弧长法进行分析。

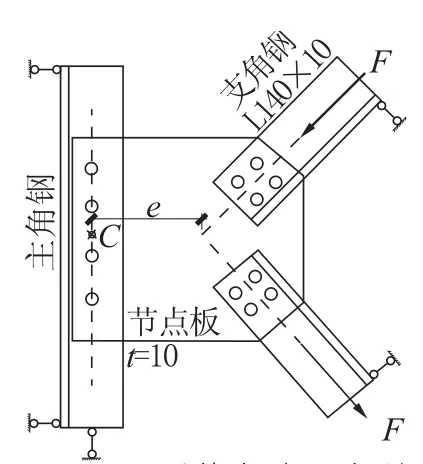
图3 K型节点边界条件Fig.3 Boundary conditions of K-joint

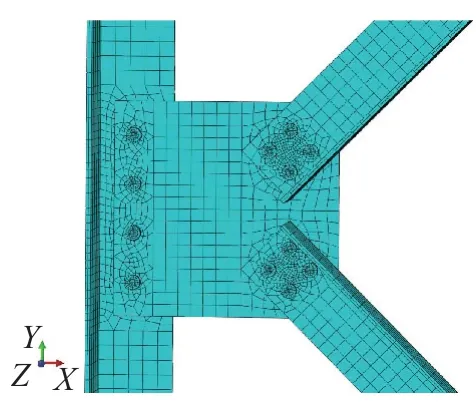
图4 K-1模型网格Fig.4 Meshing grids of K-1

2.2 计算结果分析

当F加载至310kN时，K-1模型1∶1应力云图如图5所示，整个节点产生了明显的旋转变形。在转动过程中，主角钢外侧螺栓先于内侧螺栓进入滑移状态并承担更大的荷载份额。故在进行螺栓施工安装时，若能按照由内而外的紧固顺序，则可以尽量减小外侧螺栓的组合应力，减缓其失效速度。

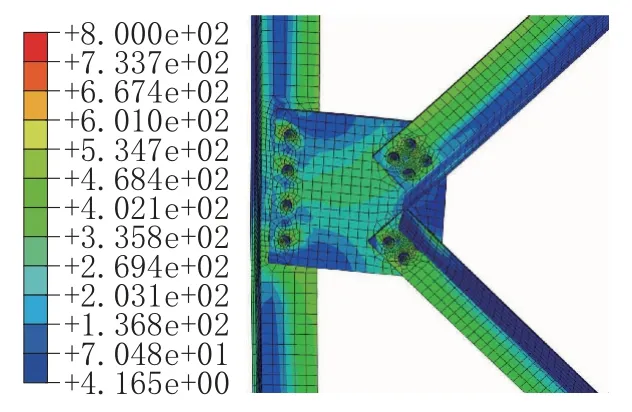
图5 K-1结果应力云图(单位：MPa)Fig.5 Stress contour(unit:MPa)

图6给出了K-1模型试验与有限元结果的弯矩-转角曲线对比。模拟曲线在大体趋势上与试验结果保持一致，但两者在初始刚度上有所差别，并且与模拟相比，试验曲线未明显体现出螺栓滑移的过程。

产生上述差别的主要原因是:螺栓与螺孔的间隙分最大间隙、理想间隙与最小间隙的差别[4]。ABAQUS模型中，所有螺栓都是按照理想间隙建模，同等受力情况下的螺栓会同时进入滑移状态。但在人工安装的试验构件中，这三种间隙可能同时存在，并且最小间隙情况下，螺栓不会产生明显滑移，故在同等受力状态下，试验中螺栓的滑移有先后差别，在图6试验曲线中，其刚度分先后两次突然减小，这便是螺栓滑移有先后顺序的细微表现。

图7给出不同螺栓等级状态下节点转动滑移曲线的对比，在滑移的前两个阶段两条曲线几乎重合，当进入滑移后两个阶段时，K-2模型刚度明显大于K-1模型刚度。因此螺栓强度对于滑移的影响仅在栓杆传力阶段后期与整个弹塑性阶段。

图8给出了不同螺栓个数情况下节点转动滑移曲线的对比，有5颗主角钢螺栓的K-3模型节点转动滑移荷载比K-1模型高出12.8%左右，而且后期滑移刚度也要高于K-1模型。故除摩擦传力阶段外，螺栓个数对于滑移的后三个阶段都有一定影响，螺栓个数增加明显提高了滑动荷载与滑移变形的刚度。

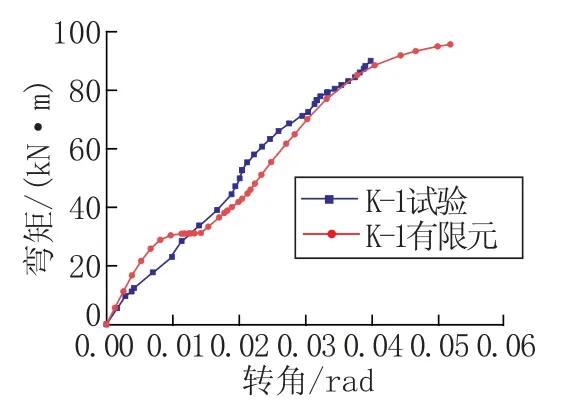
图6 K-1模型荷载位移曲线对比Fig.6 Comparison on load-deformation of K-1 model

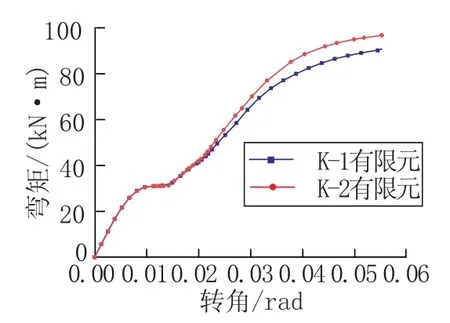
图7 K-1与K-2有限元对比Fig.7 Finite element comparison of K-1 and K-2

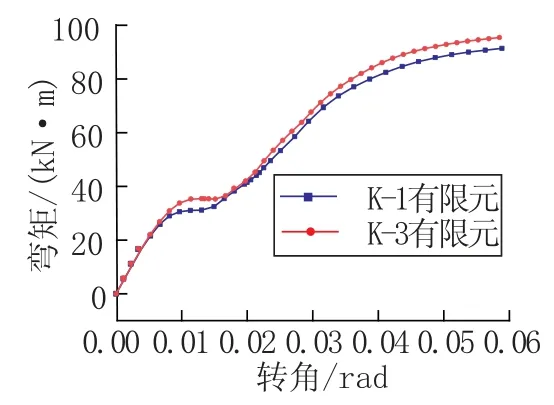
图8 K-1与K-3有限元对比Fig.8 Finite element comparison of K-1 and K-3

3 基于螺栓滑移的模型塔架计算

3.1 模型介绍

K型节点有限元模型的有效性得到验证后，本节将K型节点的转动滑移与杆件轴向滑移同时引入塔身结构分析，建立如图9、图10所示输电塔塔身模型。材料设定为Q345钢，主材采用L140mm×10mm等边角钢，斜材与横隔杆件采用L75mm×6mm角钢，塔腿辅材为L40mm×3mm角钢，塔身K型节点构造如图11所示。总共建立三个模型进行对比，除辅材采用杆单元外，其余所有构件均采用梁单元建模。

模型I:在塔身所有节点进行刚接，杆件端部没有相对位移。

模型II:在模型I的基础上，所有节点处用连接器(Connector)将斜材和横隔杆件与主材连接起来，连接方式如图12所示。其长度设置为相应杆件长度的1/1000，每个连接器均有自身的局部坐标系，约 束 连 接 器U2、U3、UR1、UR2、UR3五个相对运动自由度。只释放一个轴向相对位移U1，定义为图13所示的两颗6.8级M20螺栓沿杆件轴线方向的滑移荷载-位移曲线，使得连接器两点之间可以发生轴向滑移。

模型III:建立图11所示节点的有限元模型，并计算得出该节点在弯矩作用下的转动滑移曲线，如图14所示。在模型II基础上，于K型节点处再释放连接器(Connector)的UR3自由度，将其定义为该曲线的荷载位移关系，因此当弯矩达到滑移荷载时，亦可使节点处产生面内转动滑移。

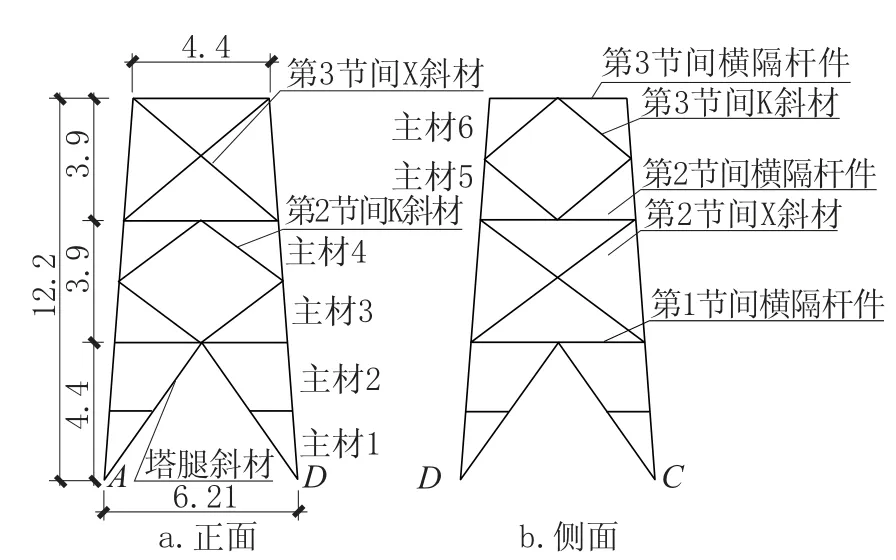
图9 模型尺寸与杆件说明(单位：m)Fig.9 Size of the model and illustration on members(unit:m)

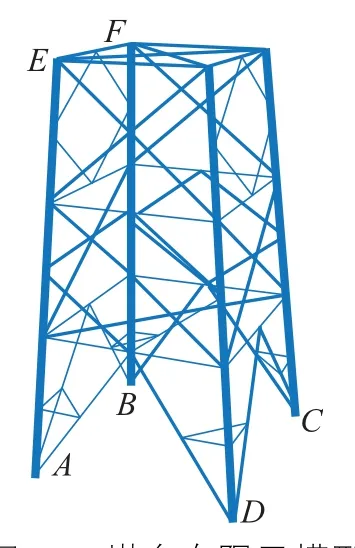
图10 塔身有限元模型Fig.10 FEA model of tower body

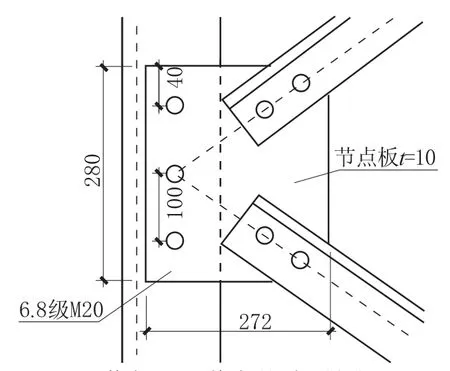
图11 塔身K型节点构造(单位：mm)Fig.11 Detail of K-joint in tower body(unit:mm)

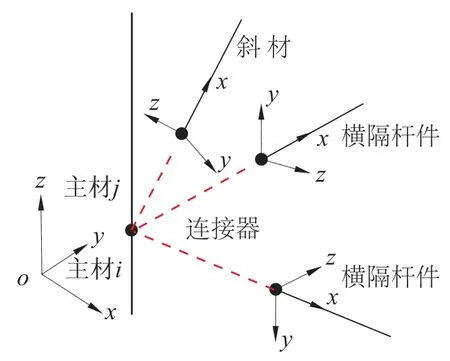
图12 节点简化模型Fig.12 Simplified model of joint

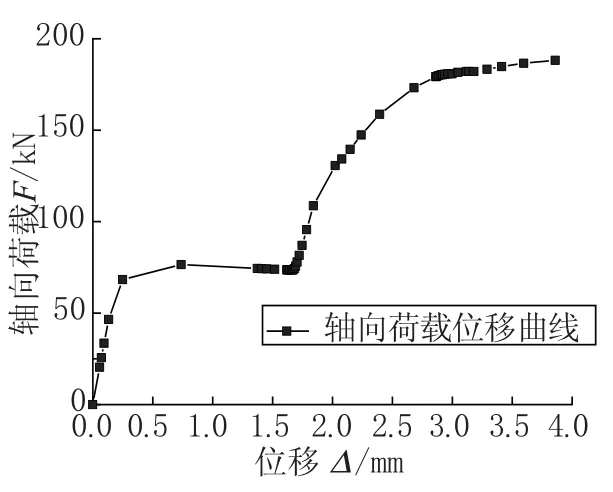
图13 轴向滑移荷载-位移曲线Fig.13 Load-deformation curve of axial slippage

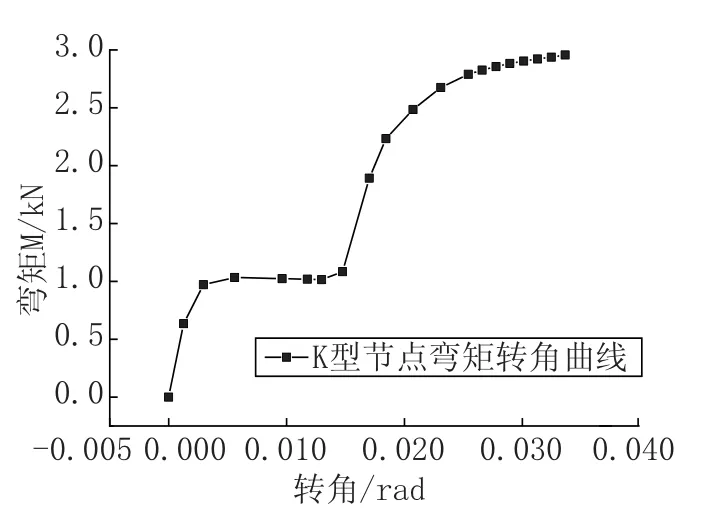
图14 节点转动弯矩-转角曲线Fig.14 Moment-rotation curve of rotational slippage

边界条件:将A、B、C、D四个塔脚全部固定约束，在塔身顶端节点E、F处施加沿总体坐标系X方向的10mm位移，研究滑移效应对杆件轴力与杆端弯矩的影响。

3.2 计算结果及影响分析

计算分析得到了各个杆件的轴力与杆端弯矩值，其结果分别见表2与表3。以下分析结果，主材取受拉一侧，横隔杆件与斜材均取正面一侧。

首先，各杆件轴力计算结果见表2。由计算结果可知，对于主材轴力，考虑轴向滑移后的模型Ⅱ比模型Ⅰ减小了8.6%～13.3%，而同时考虑了转角与轴向滑移的模型Ⅲ比仅考虑轴向滑移的模型Ⅱ减小了0.1%～0.8%左右。由此可见轴向滑移对于主材轴力影响较大，而转动滑移对其影响较小。这是因为主材与主材之间的连接通常采用包角钢或衬板进行双肢搭接，节点转动受到限制的缘故；并且由于结构荷载最终传递至塔腿，塔腿受力较大，故滑移对塔身主材的影响从上到下依次增大。

其次，对于横隔杆件，模型Ⅱ与Ⅰ相比，考虑轴向滑移后轴力减小了16.3%～36.3%，模型Ⅲ与Ⅱ相比，考虑转动滑移情况下轴力减小了2.3%～10.2%。可见两种滑移对于横隔杆件轴力影响都较大，并且从下到上影响依次减小。

最后，对于斜材，模型Ⅱ中轴力比模型Ⅰ减小了12.1%～17.3%，滑移影响从下到上依次增大。但模型Ⅲ的斜材轴力比模型Ⅱ只减小0.1%～1.5%，故转动滑移对斜材影响并不大。

总的来说，由于荷载方向沿着横隔杆件，故滑移对于横隔杆件的影响远远大于对主材与斜材的影响，比如轴向滑移对于塔身主材与斜材轴力的影响在13%左右，而对横隔杆件的影响为30%左右，是主材与斜材的2倍多。

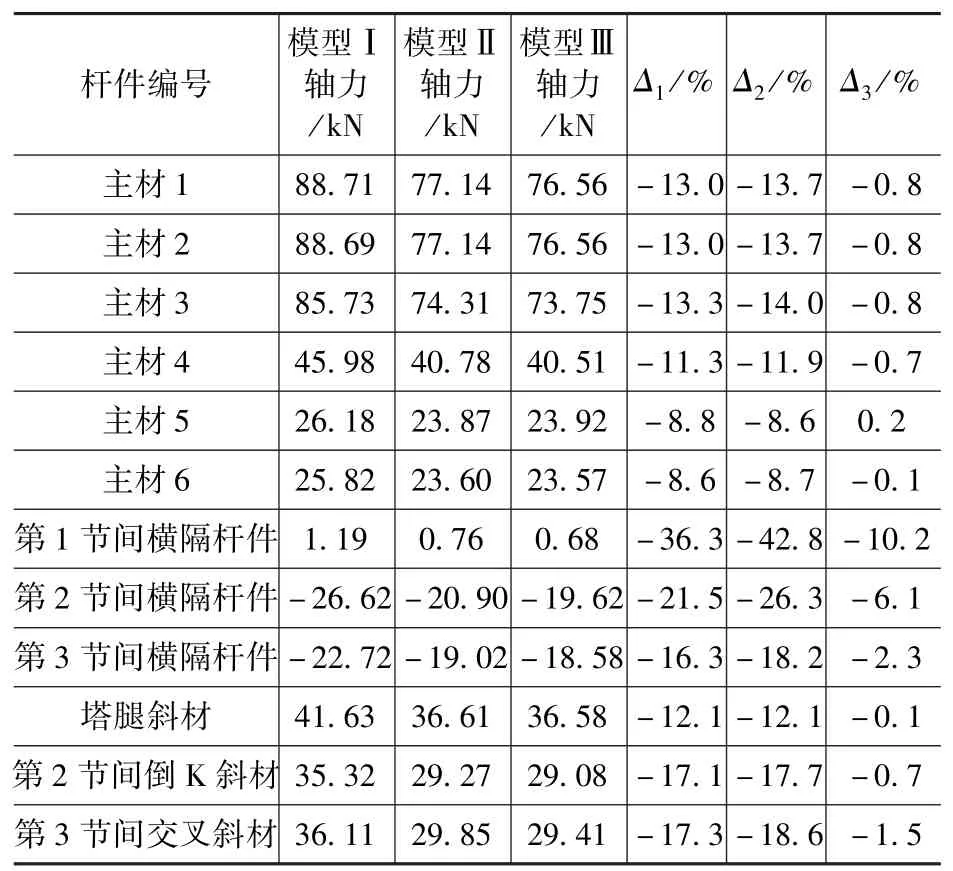
表2 三种模型杆件轴力对比Tab.2 Comparison of three models axial force

杆端弯矩见表3，各杆件杆端弯矩变化也较大。首先，对于主材，主材1的杆端弯矩取下端部截面，其余主材取杆件上端部截面。模型Ⅱ与模型Ⅰ相比，轴向滑移使中间主材3、主材4、主材5的杆端弯矩减小了7.2%～33.2%，内力转移到了上下两端主材上，其杆端弯矩增大了3.6%～89.1%；模型Ⅲ与模型Ⅱ相比，转动滑移的影响使得杆端弯矩减小了2.9%～14.9%，且从下到上影响依次减小。

其次，对于横隔杆件，模型Ⅱ比模型Ⅰ的弯矩减小了0.9%～63.6%，而模型Ⅲ与模型Ⅱ相比，转动滑移的影响大概在-32.3%～2.9%之间，且从下到上影响都依次减小。

最后，对于斜材，在轴向滑移影响下，第一二层斜材杆端弯矩分别减小了14.1%和74.3%，第三层斜材弯矩增加了74.6%。同时将模型Ⅲ与模型Ⅱ对比可以发现，转动滑移对于弯矩的影响在-23.5%～5.6%之间。

综上，考虑螺栓滑移的影响后，部分杆件杆端弯矩减小，部分杆件弯矩增大，显然螺栓滑移导致整个塔身弯矩的分布情况产生了较大变化。

表3 三种模型杆端弯矩对比Tab.3 Comparison of three models member end moment

4 结论

1.节点旋转导致主角钢外侧螺栓较内侧先进入滑移状态，因此外侧螺栓总是承担更大的荷载份额。为减小实际工程中外侧螺栓的组合应力，施工时可按照由内而外的紧固顺序进行螺栓安装。

2.螺栓强度等级对滑移曲线的一、二阶段没有影响，但对第三、四阶段有明显影响。刚度随着螺栓等级的提高而有所增大，并且增加节点主角钢螺栓个数可以有效提高其滑移荷载与节点转动刚度。

3.输电塔塔身分析中，主材与斜材的轴力受轴向滑移影响较大，受转动滑移影响较小。由于所取横隔杆件沿着荷载方向，故其轴力受到轴向与转动滑移的影响均较大。考虑螺栓滑移的影响前后，部分杆件杆端弯矩减小，部分杆件弯矩增大，螺栓滑移导致整个塔身弯矩的分布情况产生了较大变化。