Numerical investigations to design a novel model based on the fifth order system of Emden-Fowler equations
2020-11-04ZulqurninSirMehmetGiysSkrMnshukYeskindirovOnurSldir
Zulqurnin Sir*, Mehmet Giys Skr, Mnshuk Yeskindirov, Onur Sldir
a Department of Mathematics and Statistics, Hazara University, Mansehra, Pakistan
b Department of Mathematics, Faculty of Sciences, Yuzuncu Yil University, Van, Turkey
c Department of Translation Theory and Practice, L. N. Gumilyov Eurasian National University, Kazakhstan
Keywords: Fifth order Emden-Fowler system Multiple singularity Shape factor Numerical experimentations Variational iteration scheme
ABSTRACT The aim of the present study is to design a new fifth order system of Emden-Fowler equations and related four types of the model. The standard second order form of the Emden-Fowler has been used to obtain the new model. The shape factor that appear more than one time discussed in detail for every case of the designed model. The singularity at η = 0 at one point or multiple points is also discussed at each type of the model. For validation and correctness of the new designed model, one example of each type based on system of fifth order Emden-Fowler equations are provided and numerical solutions of the designed equations of each type have been obtained by using variational iteration scheme. The comparison of the exact results and present numerical outcomes for solving one problem of each type is presented to check the accuracy of the designed model.
The singular study for the researcher has achieved much importance due to the variety of applications in science, engineering and technology. The singular models are considered very interesting and sometimes become complex due to the singularity at the origin. Several singular models have different nature and vast importance exist in the literature. One of the historical and famous model is Emden-Fowler model (EFM). The research community worked to solve this historic and famous model using numerical and analytical techniques since its invention. The EFM has numerous applications in the study of fluid dynamics,relativistic mechanics, population growth, system of pattern creation and chemical reactor study. The general mathematical form of the second order EFM is given as [1-5]:
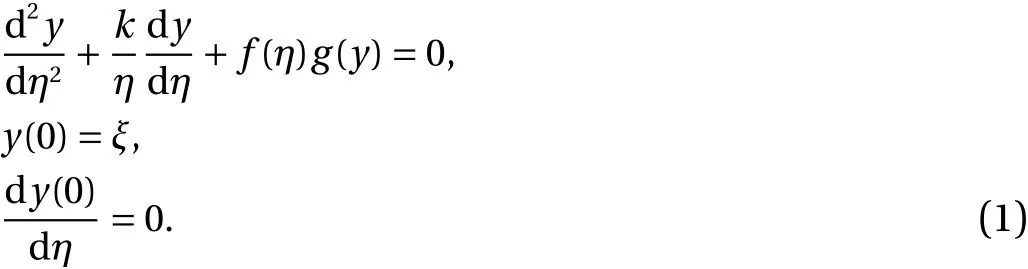
The value ofk≥1 and it represents the shape factor. The above EFM becomes Lane-Emden (LE) model by fixing the value off(η)=1, mathematically written as:

The above LE model is also singular model and has been achieved from the pioneer work of Homer Lane and Robert Emden. The LE model designates the self-gravitating gas clouds system, inner construction of polytropic stars, radiative cooling,and cluster galaxies. One can understand the importance of the singular models that have huge applications in the area of physical sciences [6], density profile of gaseous star [7], dusty fluid models [8], reactions based on catalytic diffusion [9], sublinear neutral term [10], catalytic diffusion reactions [9], electromagnetic theory [11], classical and quantum mechanics [12], mathematical physics [13], oscillating magnetic systems [14], stellar structure models [15], morphogenesis [16], and isotropic continuous media [17].
All the time the singular models were very challengeable and difficult to solve due to the involvement of singularity. There are very few existing techniques are available in literature to tackle these singular models. Only a few methods have been applied to solve such typical and stiff nature models. Some mentioned methods are Adomian decomposition scheme proposed by Shawagfeh [18] in their different works to handle the problem of singularity. Li and Rogovchenko [19] solved higher order sublinear Emden-Fowler delay differential equation. Parand and Razzaghi [20] applied a well-known numerical scheme to solve singular equations. Liao [21] used an analytic scheme to solve such singular models. Bender et al. [22] suggested a perturbative technique to handle the problem of singularity. Nouh [23] practiced to solve singular models using two schemes power series and Pade approximation. Some more detail of the singular models are given in Refs. [24-29].
The aim of the present study is to design of new model based on a fifth order system of Emden-Fowler equations along with four types. One example of the designed model has been presented and numerical experimentations have been performed by using variational iteration (VI) method. The system model for more than two variables can be extended to any form of equations. For solving the singular problems using the ordinary differential equations is much important and has many major applications in engineering and scientific applications, e.g., theory of boundary layer, reactant application in the area of chemical reactor, optimization and control theory, and network flow in the field of biology.
In this study, four different types are given based on the fifth order system of EFM. The construction of the system of fifth order EFM along with the shape factor and singular points for each type is also discussed. The initial conditions of the designed new model are achieved using the sense of standard LEM. To derive the fifth order system of Emden-Fowler equations, the mathematical form is used as:
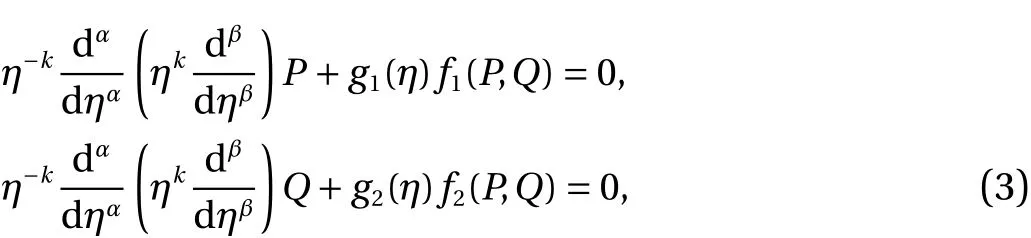
where the value of k is real and positive,g1(η) andg2(η) are given functions,f1(P,Q) andf2(P,Q) are the linear/nonlinear functions of P and Q. In order to find the system of fifth order differential equations, α and β values should be proposed as:

That makes the following four possibilities as:

Type 1
Equation (3) using α =4,β=1, becomes as:

Solving the derivative:

By solving all the steps of Eq. (9) using Eq. (10). The simple form of the designed model based on the fifth order system of EFM becomes as:
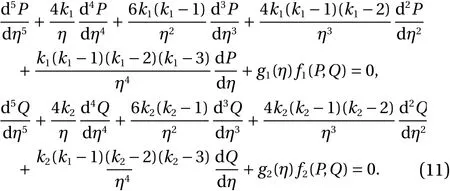
The initial conditions of the system (11) are written as:
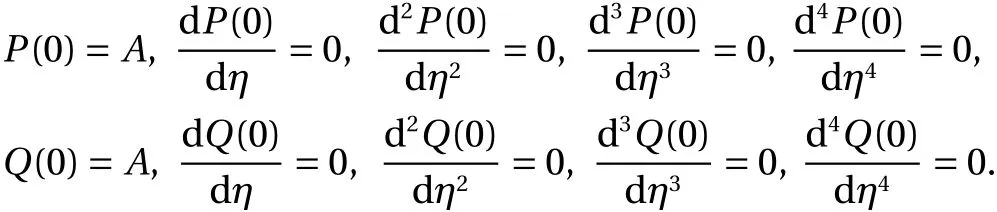
The singularity at η =0 appears four times for bothP(η) andQ(η), respectively. The shape factor is noticed4k1,6k1(k1-1),4k1(k1-1)(k1-2),andk1(k1-1)(k1-2)(k1-3) forP(η), while forQ(η) the shape factors are4k2,6k2(k2-1),4k2(k2-1)×(k2-2),andk2(k2-1)(k2-2)(k2-3).Moreover, for k = 1, the third, fourth, and fifth expression based onP(η) andQ(η) vanish. The shape factor in this case for bothP(η) andQ(η) reduces to 4. Similarly, for k = 2, the fourth and fifth expression forP(η)andQ(η) vanish in Eq. (11). The shape factors are calculated 8 and 12 in this case for second and third expression. Likewise, the shape factor values get higher for second, third and fourth terms and become 12, 36, and 24, respectively, for bothP(η) andQ(η).
Type 2
Equation (3) using α =3,β=2, becomes as:
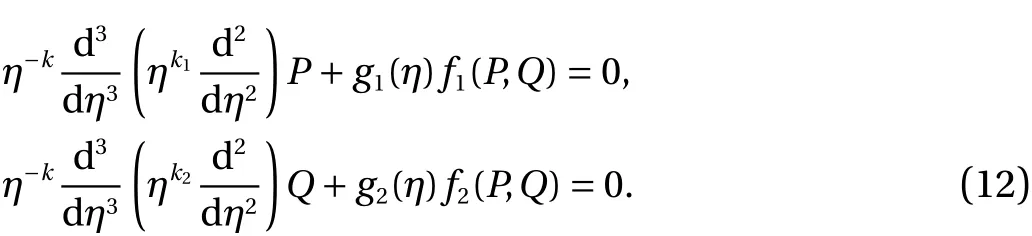
Solving the derivatives:
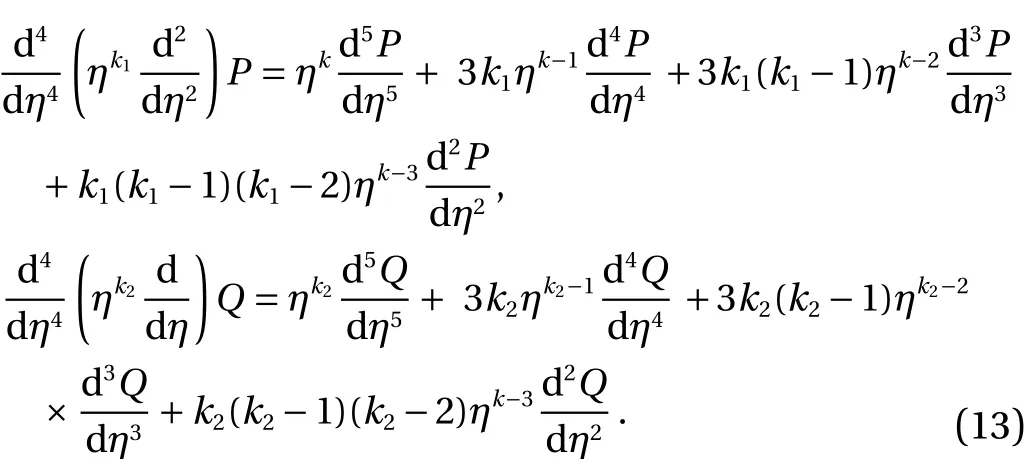
Using the above derivative values in the Eq. (12). The fifth order system of EFM becomes as: takes the form as:
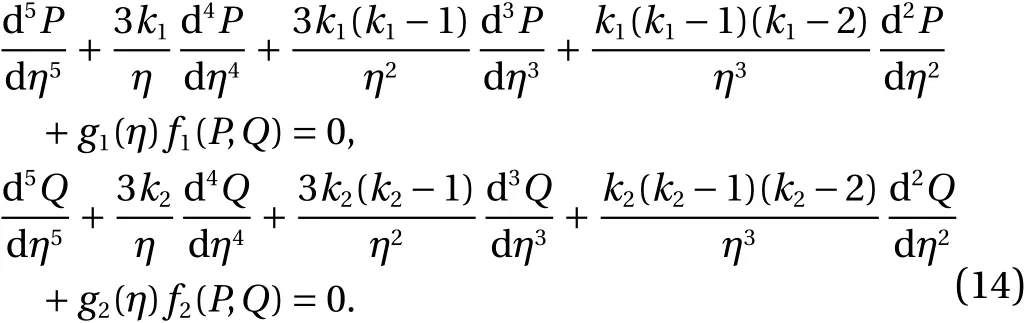
The initial conditions of the Eq. (14) are written as:
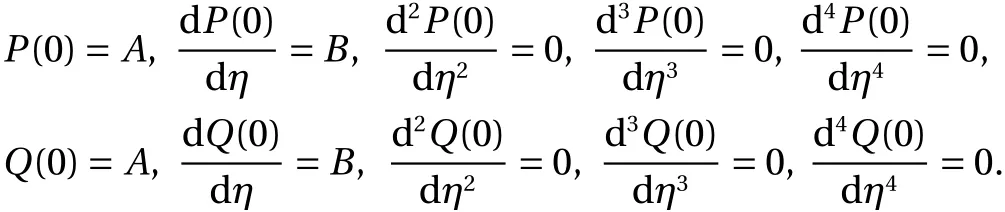
The shape factor is noticed as4k1,6k1(k1-1),4k1(k1-1)×(k1-2)andk1(k1-1)(k1-2)(k1-3) forP(η), while forQ(η)the shape factors are4k2,6k2(k2-1),4k2(k2-1)(k2-2)andk2(k2-1)(k2-2)(k2-3). The singularity at point η =0 appears three times as η=0,η2=0 andη3=0 with shape factors 3k1,3k1(k1-1)andk1(k1-1)(k1-2) forP(η), while forQ(η)the shape factors are 3k2,3k2(k2-1)andk2(k2-1)(k2-2), respectively. Moreover, the third and fourth expressions vanish for k = 1 and the shape factor reduces to 3. Likewise, for k = 2, the fourth expression becomes zero and the shape factors for second and third expression are 6 and 6, respectively.
Type 3
Equation (3) using α =2,β=3, becomes as:

Solving the derivatives:
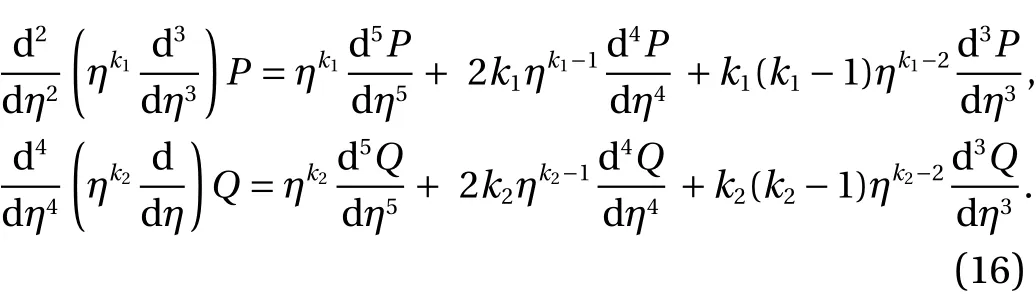
Using the above value in Eq. (15). The system of fifth order EFM takes the form as:
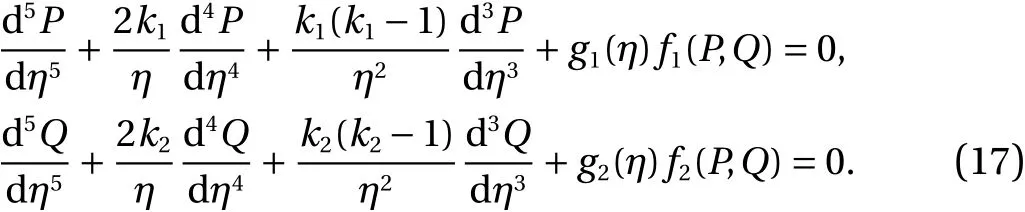
The initial conditions of the Eq. (17) are written as:

The singularity at η =0 appears two times asη=0,and η2=0 with shape factors 2k1andk1(k1-1) forP(η), while forQ(η) the shape factors are 2k2andk2(k2-1). In this case, the third expression vanishes for k = 1, and the reduced shape factor becomes 2.
Type 4
Equation (3) using α =1,β=4, becomes as:
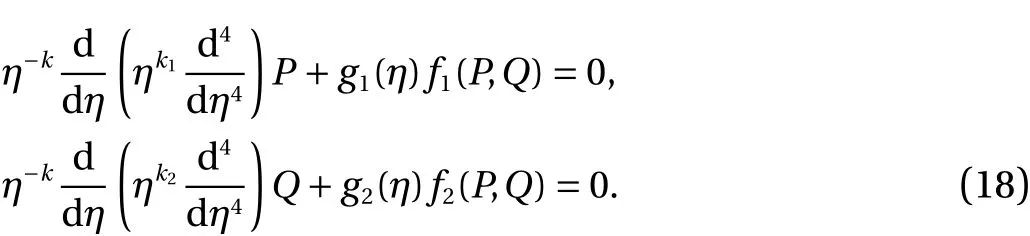
Solving the derivatives:

Using the above value in Eq. (18). The system of fifth order EFM takes the form as:
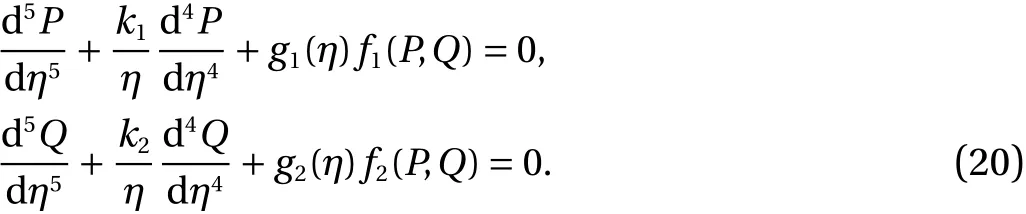
The initial conditions of the above system is written as:
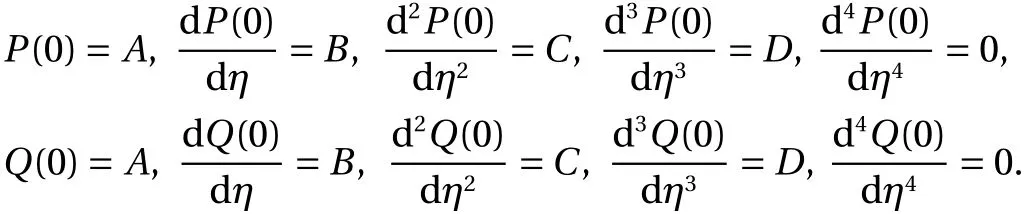
The singularity at η =0 appears one time as η =0 with shape factorsk1forP(η), while forQ(η) the shape factor isk2. In this section, one example of each type based on the designed model fifth order system of Emden-Fowler equations are presented. In this type, one example based on fifth order LE will be discussed.The Example 1 is achieved takingk1=k2=4 in Eq. (11).
Example 1.Consider the nonlinear multi-point fifth order system of LE equation is:
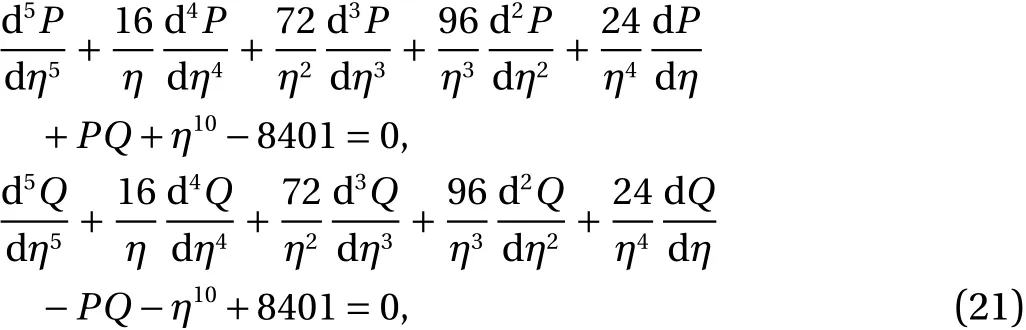
the initial conditions are

The exact solution of Eq. (21) isIn this type, one example based on the system of fifth order EFM will be discussed by taking k = 3 in Eq. (14).
Example 2.Consider the fifth order system of equation based on EFM is given as:
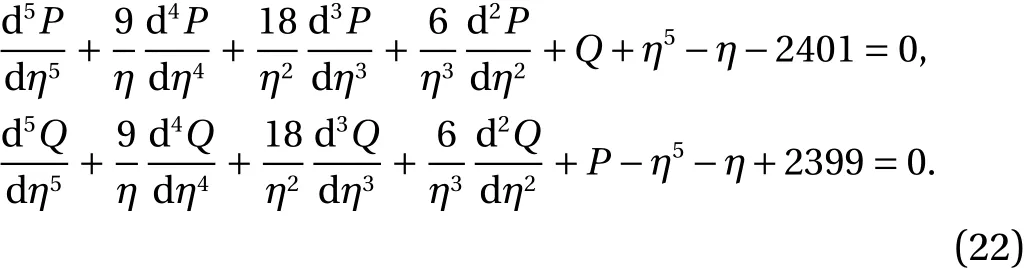
The initial conditions are
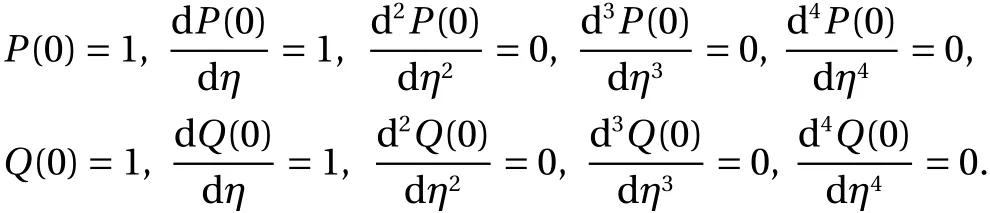
The exact solution of Eq. (22) isThe modeled equations of type 3 are achieved by taking k = 2 in Eq. (17).
Example 3. Consider the system of EFM is given as:
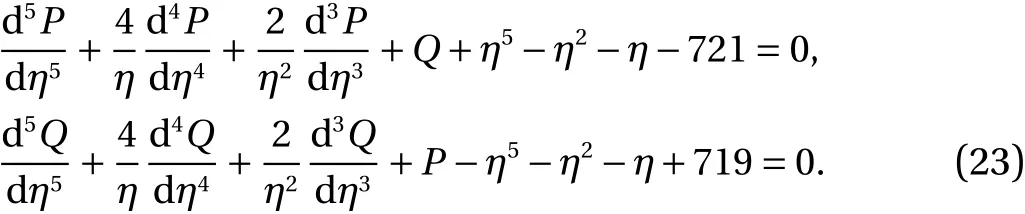
The initial conditions are

The exact solution of Eq. (23) isThis type of fifth order system of EFM is achieved by taking k = 1 in Eq. (20).
Example 4.Consider the system of fifth order EFM is given as:
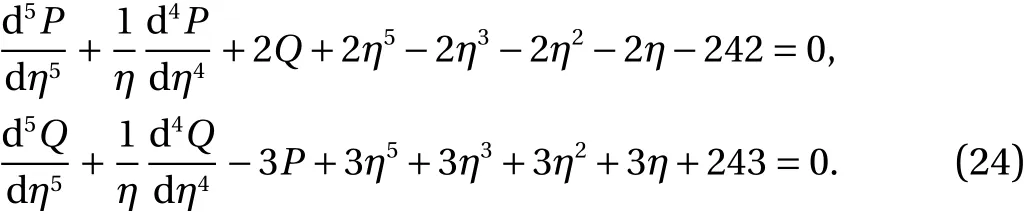
The initial conditions are
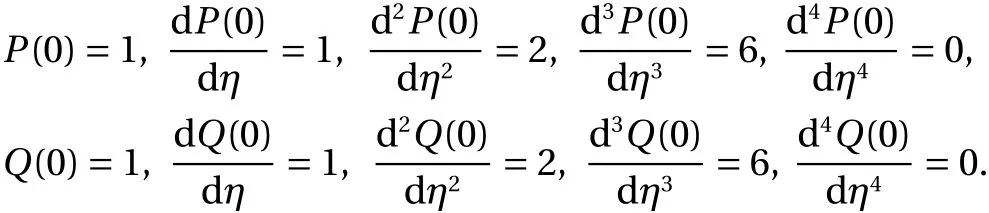
The exact solution of Eq. (24) is
In this section, the detail of the VI method along with the solution of each type is presented. The results are plotted in the form of figures of each type. To understand the basic idea of the VI method [30-32], the following differential equation is considered as:

In the above expression L and N represent linear and nonlinear operators andis used as a nonhomogeneous term. According to VI method, a correction functional can be written as follows:
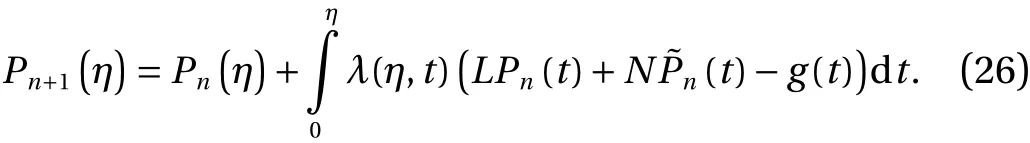

Type 1: VI method
In order to apply the VI method in the first type, the correction functional takes the form as:
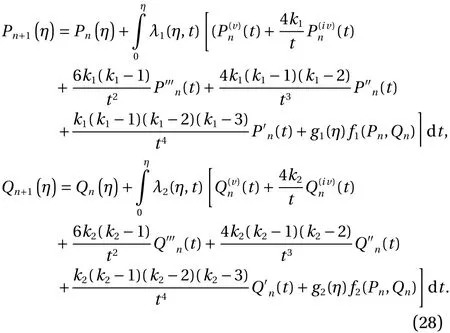
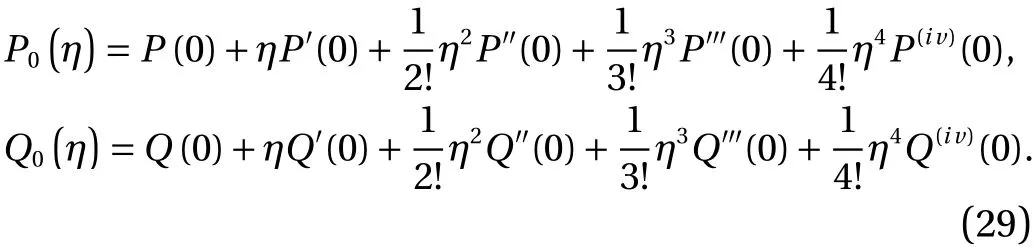

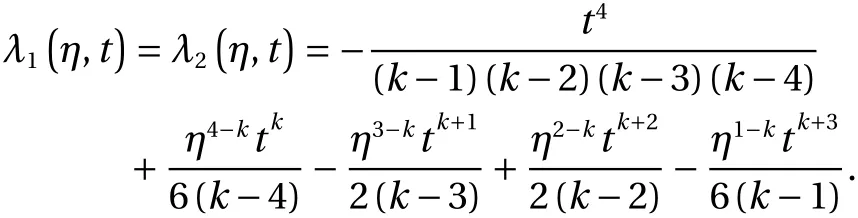
(2) Fork1=k2=1, LMs take the form as:
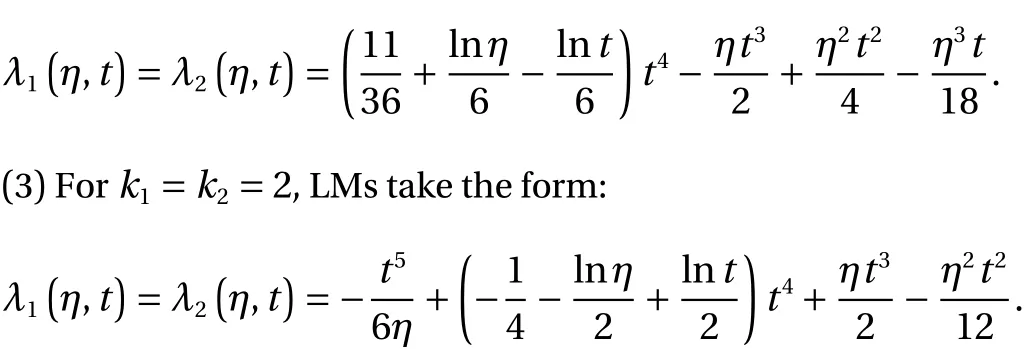
(4) Fork1=k2=3, LMs take the form as:
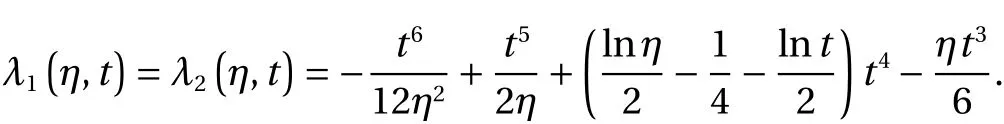
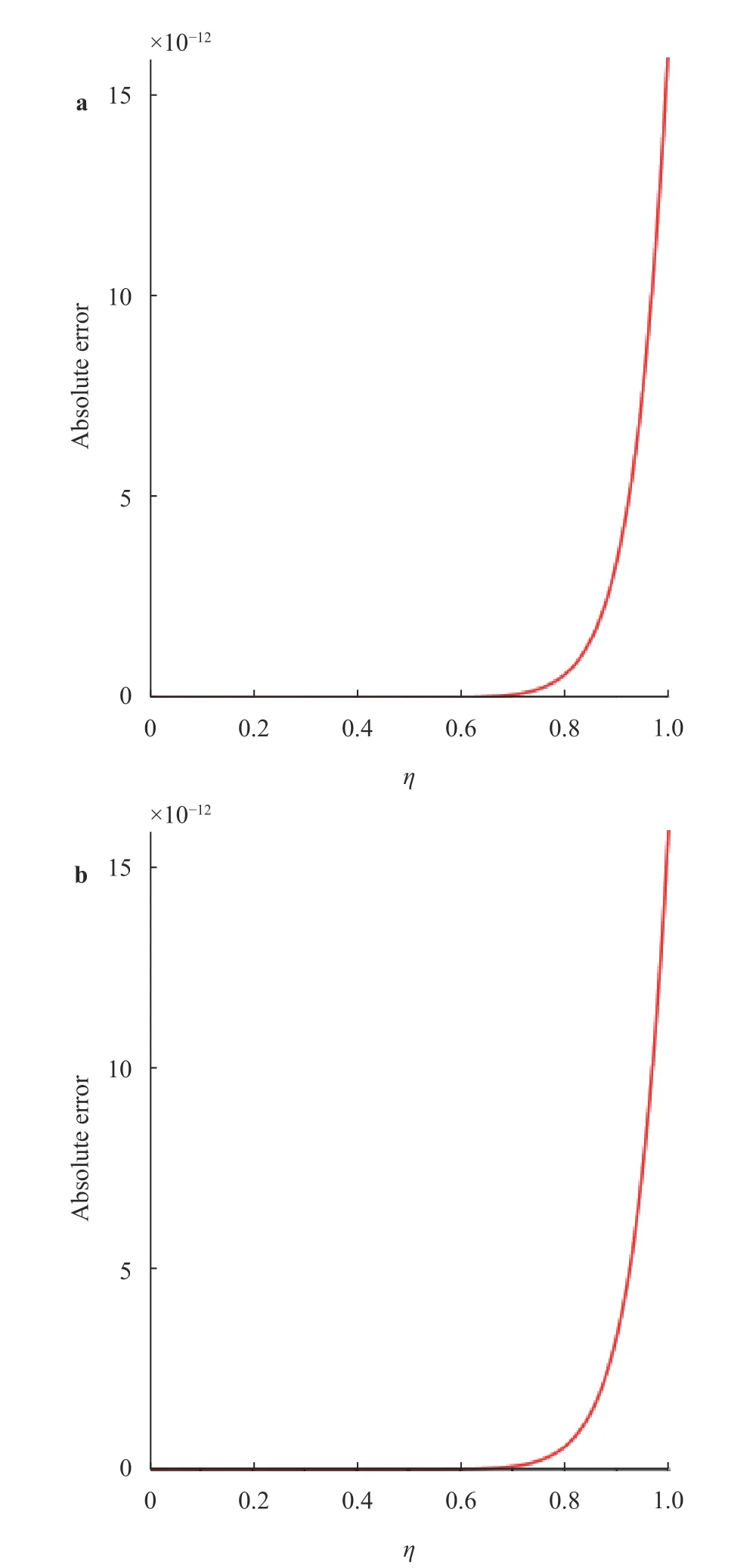
(5) Fork1=k2=4, LMs become as:
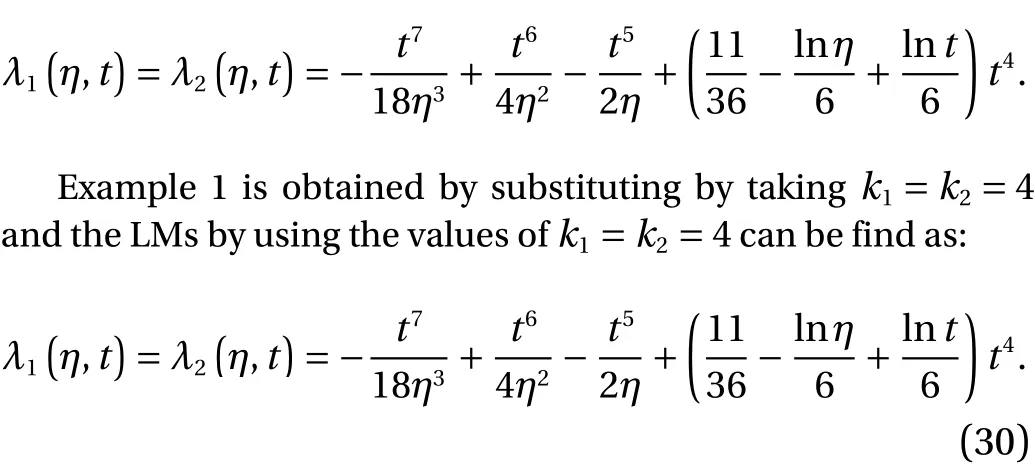
P(η) Q(η)Fig. 1. AE values of Example 1 for and .


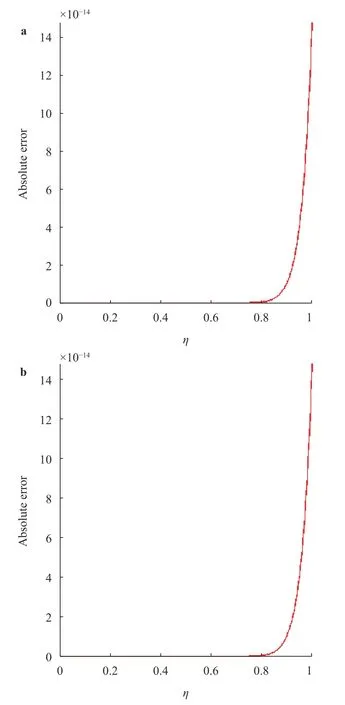
P(η) Q(η)Fig. 2. AE values of Example 2 for and .

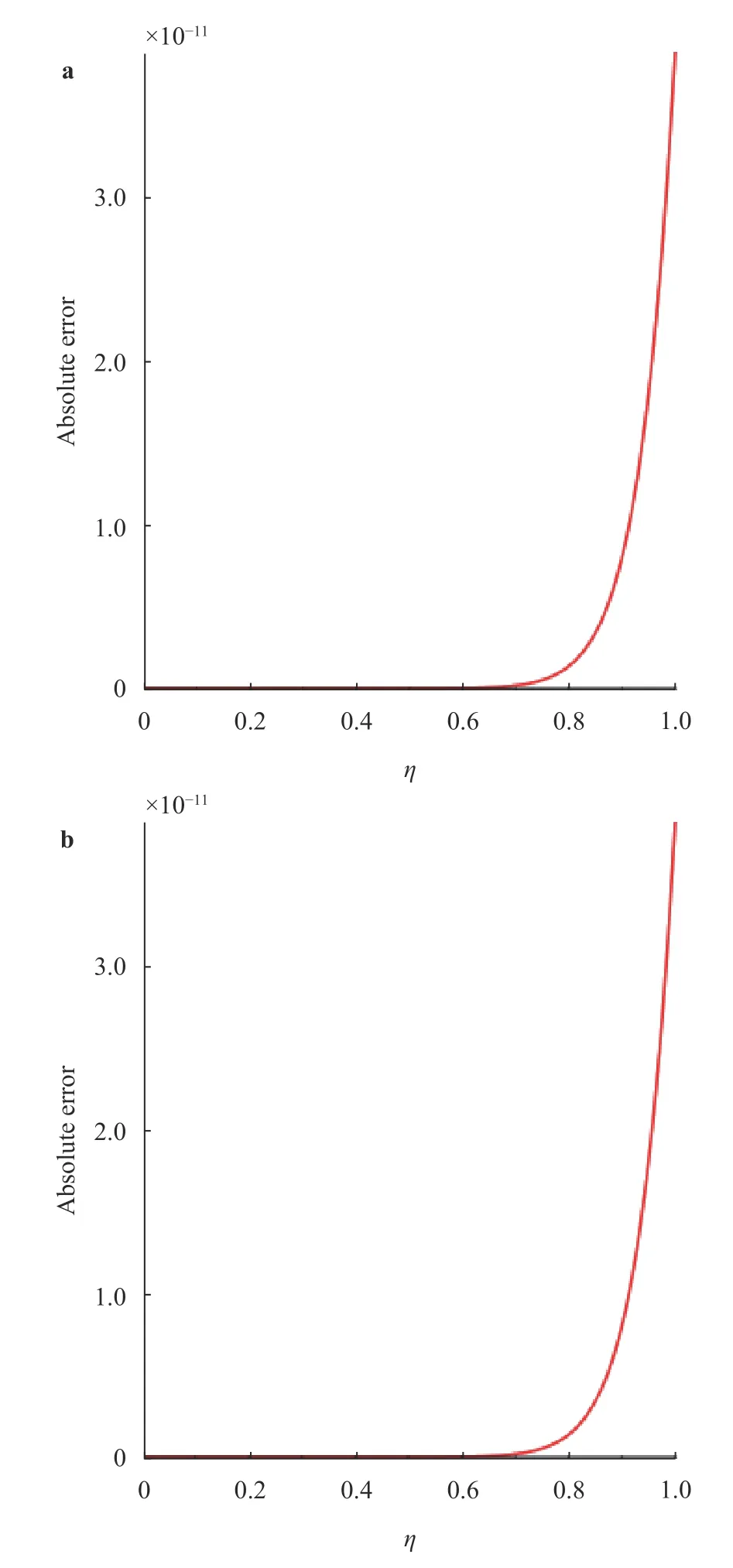
P(η) Q(η)Fig. 3. AE values of Example 3 for and .



P(η) Q(η)Fig. 4. AE values of Example 4 for and .


In this study, a new model based on the fifth order system of Emden-Fowler equations have been presented by using the sense of second order EFM. Four types of the designed modeled equations are also presented along with the numerical example of each type. The singular points and the shape factors of the modeled equations of each type are discussed in detail. The singularity at= 0 appears a single time in the standard Emden-Fowler equation, while in this study, the singularity arises four times in type 1, three times at type 2, twice in type 3 and one time in the last type of the system of fifth order Emden-Fowler model. Likewise, the shape factor in the standard form of the EFM is unique, but different shape factors have been noticed for every type of the designed model. Furthermore,one example of each type based on the designed model is modeled and numerical investigations have been made by using the variational iteration method. The values of the AE lie around 10-14to 10-10for each case of the designed model, which proves the stability of the designed model. One may observe that the accuracy of the designed scheme can be enhanced by using the higher-order approximate solutions. Moreover, comparison of the obtained results obtained by the variational iteration scheme with the exact solution of each type shows the correctness and the perfection of the designed fifth order system of EFM.
In the future, different types of singular higher order models and the system of these higher order models can be designed by considering the sense of the standard form of the Emden-Fowler equation and solutions can be presented by using the artificial neural networks [35-41].
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- A unidirectional SH wave transducer based on phase-controlled antiparallel thickness-shear (d15) piezoelectric strips
- A novel method for investigation of acoustic and elastic wave phenomena using numerical experiments
- A note on a family of proximal gradient methods for quasi-static incremental problems in elastoplastic analysis
- Modeling rock fragmentation by coupling Voronoi diagram and discretized virtual internal bond
- Dynamic mode decomposition and reconstruction of transient cavitating flows around a Clark-Y hydrofoil
- Ultrasound calibration with ladder phantom at multiple depths for breast biopsy navigation system
