A note on a family of proximal gradient methods for quasi-static incremental problems in elastoplastic analysis

Yoshihiro Kanno*

Mathematics and Informatics Center, University of Tokyo, Hongo 7-3-1, Tokyo 113-8656, Japan

Keywords: Elastoplastic analysis Incremental problem Nonsmooth convex optimization First-order optimization method Proximal gradient method

ABSTRACT Accelerated proximal gradient methods have recently been developed for solving quasi-static incremental problems of elastoplastic analysis with some different yield criteria. It has been demonstrated through numerical experiments that these methods can outperform conventional optimization-based approaches in computational plasticity. However, in literature these algorithms are described individually for specific yield criteria, and hence there exists no guide for application of the algorithms to other yield criteria. This short paper presents a general form of algorithm design, independent of specific forms of yield criteria, that unifies the existing proximal gradient methods. Clear interpretation is also given to each step of the presented general algorithm so that each update rule is linked to the underlying physical laws in terms of mechanical quantities.

In these 15 years, it has become a trend to apply constrained convex optimization approaches to diverse problems in computational plasticity. Particularly, secondorder cone programming(SOCP) and semidefinite programming (SDP) have drawn considerable attention; see Refs. [1-7] for SOCP approaches, Refs.[8-14] for SDP approaches, and Ref. [15] for recent survey on numerical methods in plasticity. Most of these approaches make use of interior-point methods; particularly, it is known that primal-dual interior-point methods can solve SOCP and SDP problems in polynomial time, and in practice require a reasonably small number of iterations [16].

Recently, accelerated proximal gradient methods have been developed for solving quasi-static incremental problems in elastoplastic analysis of trusses [17] and continua with the von Mises [18] and Tresca [19] yield criteria. In contrast to SOCP and SDP approaches, these methods solve unconstrained nonsmooth convex optimization formulations of incremental problems. Through numerical experiments [18, 19], it has been demonstrated that the accelerated proximal gradient methods outperform SOCP and SDP approaches using a standard implementation of a primal-dual interior-point method.

The proximal gradient method is a first-order optimization method, which uses function values and gradients to update an incumbent solution at each iteration; in other words, first-order optimization methods do not use the Hessian information of functions. In contrast, the interior-point method is a second-order optimization method, which makes use of the Hessian information. It is usual that first-order methods need only very small computational cost per iteration but show slow convergence, compared with second-order methods. Recently, accelerated versions of first-order methods have been extensively studied especially for solving large-scale convex optimization problems [20-24]. Such accelerated first-order methods originate Nesterov [25, 26]. These methods show locally fast convergence,while computational cost per iteration is still very small. Also,most of them are easy to implement. Particularly, the accelerated proximal gradient method [22, 27] has many applications in data science, including regularized least-squares problems [28,29], signal and image processing [22, 30], and binary classification [31]. This success of the accelerated proximal gradient method in data science supports that it can also be efficient especially for large-scale problems in computational plasticity,compared with conventional second-order optimization methods.

The idea behind our use of accelerated first-order optimization methods for equilibrium analysis of structures can be understood as follows. For simplicity, consider static equilibrium analysis of an elastic structure. Letu∈Rddenote the nodal displacement vector, wheredis the number of degrees of freedom.We useπ(u) to denote the elastic energy stored in the structure.For a specified static external load vectorq∈Rd, the total potential energy is given asπ(u)-q·u. The equilibrium state is characterized as a stationary point of this total potential energy function. Application of the steepest descent method (which is a typical first-order method) to the minimization problem ofπ(u)-q·uresults in the iteration

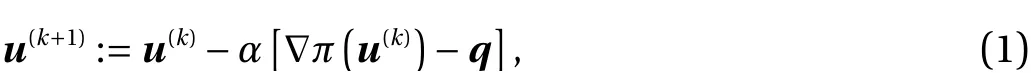
whereα＞ 0 is the step length. Here,∇π(u(k))-qon the right side is the unbalanced nodal force vector (i.e., the residual of the force-balance equation) atu(k). Thus, the computation required for each iteration in Eq. (1) is very cheap, compared with an iteration of a second-order method, e.g., the Newton-Raphson method (which needs to solve a system of linear equations).However, it is well known that the steepest descent method spends a large number of iterations before convergence: The sequence of objective values generated by the steepest descent method converges to the optimal value at a linear rate [32]. To improve this slow convergence, we may apply Nesterov’s acceleration to Eq. (1), which yields the iteration

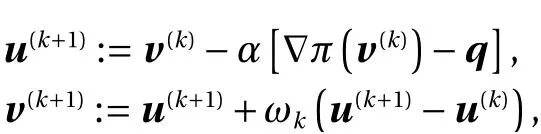
whereωk＞ 0 is an appropriately chosen parameter [25, 26]. We can see that the computation required for each iteration is still very cheap. In contrast, the convergence rate is drastically improved: under several assumptions such as strong convexity ofπ, local quadratic convergence is guaranteed [25, 26]. In practice, we also incorporate the adaptive restart of acceleration[24], to achieve monotone decrease of the objective value.Indeed, for elastic problems with material nonlinearity, the numerical experiments in Ref. [33] demonstrate that the accelerated steepest descent method outperforms conventional second-order optimization methods, especially when the size of a problem instance is large.

The total potential energy for an elastoplastic incremental problem is nonsmooth in general, due to nonsmoothness of the plastic dissipation function. Therefore, unlike an elastic problem considered above, application of the (accelerated) steepest descent method is inadequate. Instead, as shown in Refs.[17-19], the (accelerated) proximal gradient method is well suited for elastoplastic incremental problems. In Refs. [17-19],although the concrete steps of the algorithms are presented, it is not explained how these steps correspond to the underlying physical laws in terms of quantities in mechanics. This short paper presents a clearer understanding of this correspondence relation. Moreover, in Refs. [17-19], for each specific yield criterion an algorithm is described individually, and hence comprehensive vision of algorithm design is not presented. This paper provides a general scheme for algorithm design, independent of specific forms of yield criteria. With these two contributions, this paper attempts to provide a deeper understanding of(accelerated) proximal gradient methods for computational plasticity.

We are now in position to formally state the problem considered in this paper. Namely, we consider a quasi-static incremental problem of an elastoplastic body, where small deformation is assumed. Although the proximal gradient methods in Refs. [17-19] deal with the strain hardening, in this paper we restrict ourselves to perfect plasticity (i.e., a case without the strain hardening) for the sake of simplicity of presentation.

Consider an elastoplastic body discretized according to the conventional finite element procedure. Suppose that we are interested in quasi-static behavior of the body in the time interval[0,T]. This time interval is subdivided into some intervals. For a specific subinterval, denoted by [t,t+ Δt], we apply the backward Euler scheme and attempt to find the equilibrium state att+ Δt.

Letdandmdenote the number of degrees of freedom of the nodal displacements and the number of the evaluation points of the Gauss quadrature, respectively. We use Δu∈Rdto denote the incremental nodal displacement vector. At numerical integration pointl(l= 1, 2, ...,m), let Δεel∈S3and Δεpl∈S3denote the incremental elastic and plastic strain tensors, respectively,whereS3denotes the set of second-order symmetric tensors with dimension three. The compatibility relation between the incremental displacement and the incremental strain is given as

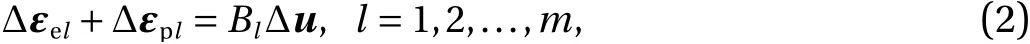
whereBlis a linear operator.

Letσl∈S3(l=1,2,...,m) andq∈Rddenote the stress tensor and the external nodal load at timet+ Δt. The force-balance equation is written as

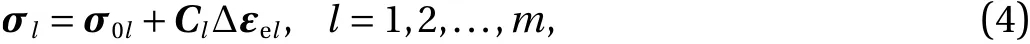
Letσ0l∈S3denote the (known) stress at timet. The constitutive equation is written as whereClis the elasticity tensor. LetYl⊂S3denote the admissible set of stress, where the boundary ofYlcorresponds to the yield surface. As usual in plasticity, we assume thatYlis a nonempty convex set. LetδYl:S3→R∪{+∞} denote the indicator function ofYl, i.e.,

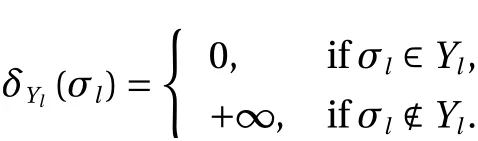
The postulate of the maximum plastic work is written as [34, 35]

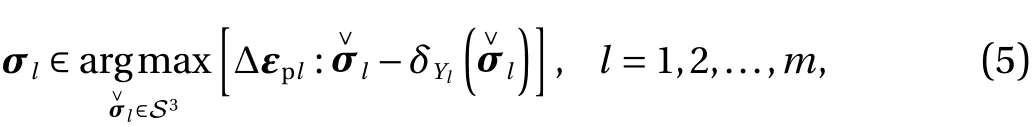
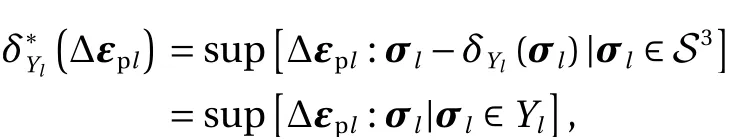
which is called the dissipation function [34] (in convex analysis,is known as a support function ofYl[36]).It is worth noting thatis a closed proper convex function. We useto denote the subdifferential ofati.e.,

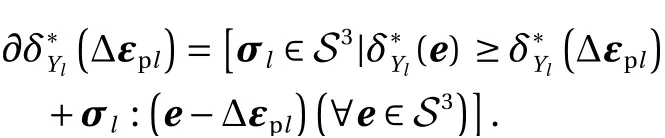
As a fundamental result of convex analysis, Eq. (5) is equivalent to (for a closed proper convex functionf: Rn→R∪{+∞}, it is known thatis equivalent to

Accordingly, the incremental problem to be solved is formulated as Eqs. (2)-(6), where Δεel, Δεpl,σl(l= 1, 2, ...,m), and Δuare unknown variables.

For a specific yield criterion, a proximal gradient method was individually proposed in each of Refs. [17-19]. The following, we present a unified perspective of these methods by providing a general form of a proximal gradient method solving a general elastoplastic incremental problem in Eqs. (2)-(6). Also, from a mechanical point of view, clear interpretation is given to each step of the iteration.

We begin by observing that Δεelcan be eliminated by using Eq. (2). Then the increment of the stored elastic energy associated with the Gauss evaluation pointl(l= 1, 2, ...,m) can be written as

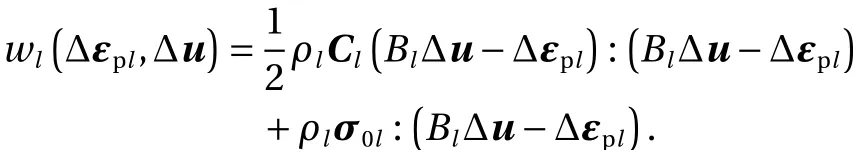
This is a convex quadratic function, becauseClis a constant positive definite tensor. Accordingly, the minimization problem of the total potential energy is formulated as follows

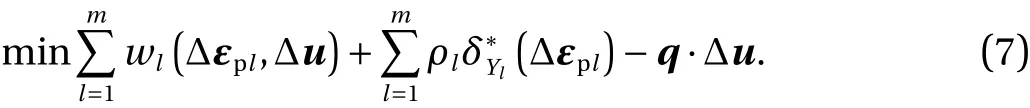
Here,q·Δuis the scalar product ofqand Δu. The optimality condition of problem Eq. (7) corresponds to Eqs. (2)-(4) and (6);see, for more accounts with specific yield criteria [17-19, 35] .

For a closed convex functionf:S3→R∪{+∞}, let proxf:S3→S3denote the proximal operator off, which is defined by

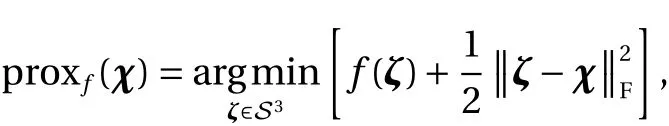
for a nyχ∈S3, whereis the Frobenius norm ofζ-χ,A proximal gradient method applied to problem (7) consists of the iteration

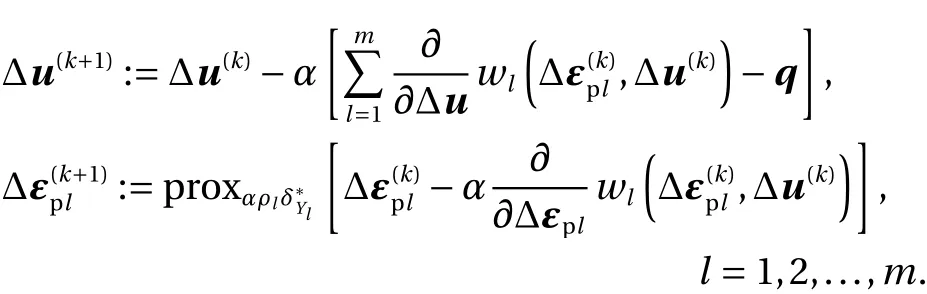
Here, α ＞ 0 is a step length. For the guarantee of convergence we et α ≤ 1/L [22, 27], where L denotes the maximum eigenvalue of the Hessian matrix of . A short calculation shows that the iteration above can be written in an explicit manner as Algorithm 1.∑ml=1 wl(Δεpl,Δu)

Example 1. As a simple example, consider a truss consisting ofmbars. For truss elementl(l= 1, 2, ...,m), we useσland Δεplto denote the axial stress and the incremental axial plastic strain,respectively. The set of admissible stress is given as

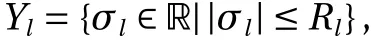
whereRlis the magnitude of the yield stress. Then the dissipation function is

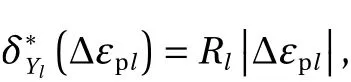
which is depicted in Fig. 1a. The proximal operator ofused in line 6 of Algorithm 1, is

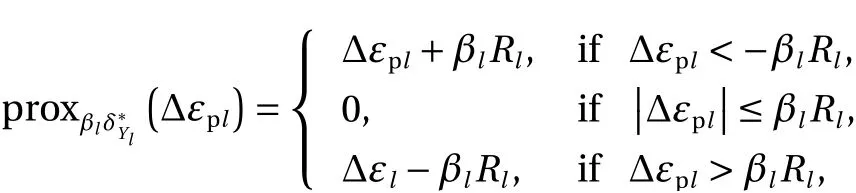
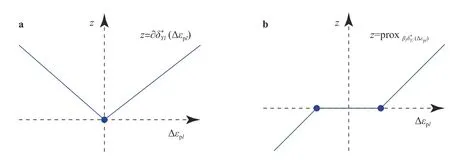
Fig. 1. Dissipation function of Example 1 and its proximal operator.

which is depicted in Fig. 1b; see Ref. [17] for details.

Each iteration of Algorithm 1 consists of the following procedures. In line 2, according to the compatibility relations, we update the incremental elastic strains, by using the incumbent incremental displacement and the incumbent incremental plastic strains. In line 3, we update the stress tensors according to the constitutive equations. In line 4, we compute the unbalanced nodal force vector,r(k), according to the force-balance equation. Line 5 updates the incremental displacement vector,by adding -αr(k)to the incumbent solution, Δu(k). This update rule is analogous to the steepest descent method applied to an elastic problem [33]; see Eq. (1). Line 6 updates the incremental plastic strains, where the proximal operator of the dissipation function (scaled byβl) is used. This step is further discussed later.

The computations of Algorithm 1, except for the one in line 6,consist of additions and multiplications, which are computationally very cheap; it is worth noting thatBl(l= 1, 2, ...,m) is usually sparse. For the computation in line 6, explicit formulae have been given for the truss [17], von Mises [18], and Tresca [19]yield criteria. Therefore, for these yield criteria, the computation in line 6 is also cheap. Thus, to extend this algorithm to another yield criterion, it is crucial to develop an efficient computational manner for line 6.

It is worth noting that, in practice, we incorporate the acceleration scheme [22] and its restart scheme [24] into Algorithm 1,to reduce the number of iterations required before convergence;see Refs. [17-19]. Also, every step of Algorithm 1 is highly parallelizable. Namely, the computations in lines 2, 3, and 6 are carried out independently for each numerical integration point, and the vector additions in lines 4 and 5 can be performed independently for each row.

We next provides an interpretation of Algorithm 1 from a perspective of a fixed-point iteration. A key is the following property of the proximal operator.

Lemma 1.Let f:S3→R∪{+∞} be a closed proper convex function andγ＞ 0. Forχ,ζ∈S3, we haveζ= proxγf(χ) if and only ifχ=ζ+γ∂f(ζ).

Proof. See section 3.2 of Ref. [27].

In accordance with lines 2 and 3 of Algorithm 1, we write

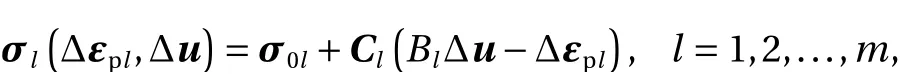
for notational simplicity, whereσl(Δεpl, Δu) is the incumbent stress determined from Δεpland Δu. It follows from Eq. (3) that the unbalanced nodal force vector (i.e., the residual of the forcebalance equation) can be written as

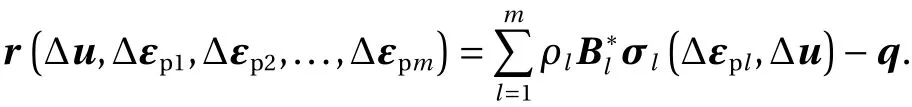
Then the system of Eqs. (2)-(6) is equivalently rewritten as

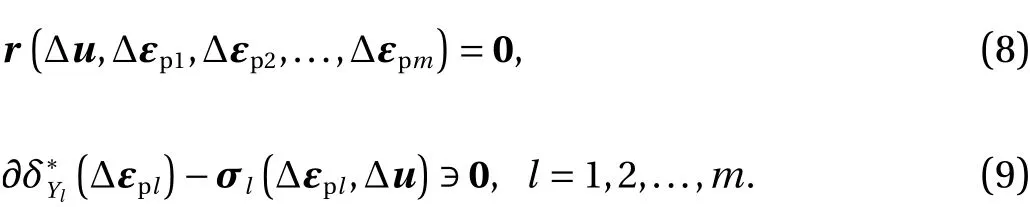
We easily see that, for anyα＞ 0 andβl＞ 0 (l= 1, 2, ...,m), Eqs. (8)and (9) are satisfied if and only if

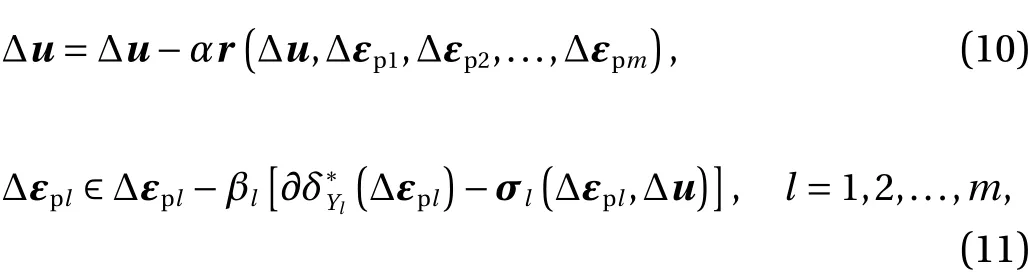
hold. That is, the solution of the elastoplastic incremental problem is characterized as a fixed point of the mappings on the right sides of Eqs. (10) and (11).

A natural fixed-point iteration applied to Eq. (10) is

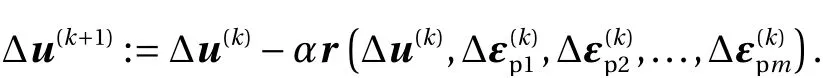
This is exactly same as the computations in lines 2-5 of Algorithm 1.

In contrast, we apply a slightly different scheme to Eq. (11).Namely, for eachl= 1, 2, ...,mwe rewrite Eq. (11) equivalently as

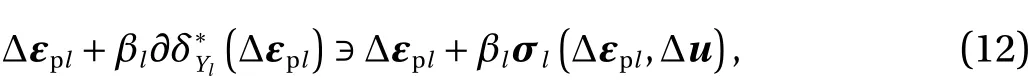
from which we obtain an iteration

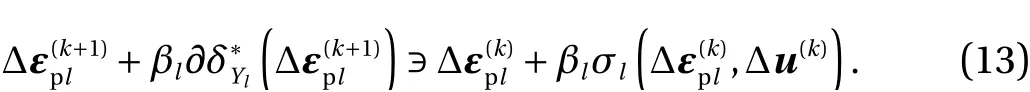
It follows from Lemma 1 that Eq. (13) is equivalent to

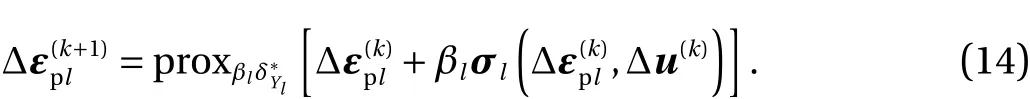
This corresponds to line 6 of Algorithm 1. Since application of the proximal operator of a closed proper convex function to any point always results in a (nonempty) unique point [27], the right side of Eq. (14) is guaranteed to be uniquely determined.

Remark1. We have seen that the update rule of the plastic strain, Eq. (14), of Algorithm 1 can be obtained not from Eq. (11)but from Eq. (12). If we adopt Eq. (11), application of a fixed-point iteration yields

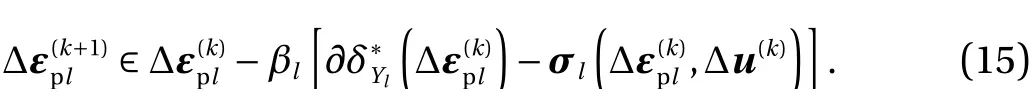
However, this is not adequate as an update rule, becauseon the right side of Eq. (15) is, in general, not determined uniquely. For example, in the truss case considered in Example 1, Fig. 2 showswhereis shown in Fig. 1a. It is observed in Fig. 2 thats not unique at Δεpl= 0. In contrast, as mentioned above,satisfying Eq.(13) exists uniquely, which makes Algorithm 1 well-defined.

Remark 2. To provide another viewpoint, observe that Eq.(13) is equivalently written as

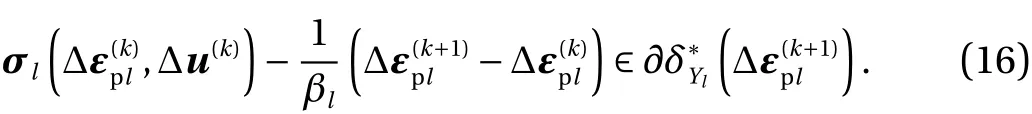
This is analogous to the associated flow rule in Eq. (6), but the second term on the left side seems to be additional. One may consider that a natural update rule based on Eq. (6) is

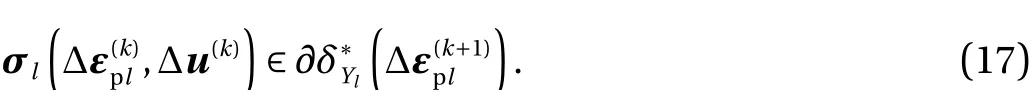
However, Eq. (17) is not adequate, because forthere exists nosatisfying Eq. (17);see Fig. 2 for the truss case. In contrast, as mentioned above, for anyandsatisfying Eq. (16) exists uniquely.

In summary, this short paper has presented a unified form of proximal gradient method to solve quasi-static incremental problems in elastoplastic analysis of structures. An interpretation of the presented algorithm has also been provided from a viewpoint of mechanics. Although in this paper we have restricted ourselves to perfect plasticity, extension of the presented results to problems with strain hardening is possible; one can refer to Refs. [17-19] for cases with specific yield criteria.

The presented general form of the algorithm, as well as interpretation, sheds new light on numerical methods in computational plasticity. For example, although this paper has been restricted to quasi-static incremental problems, it can possibly provide us with a guide for development of similar algorithms solving other problems in plasticity, including, e.g., limit analysis and shakedown analysis. Such algorithms combined with an acceleration scheme may possibly be efficient compared with conventional methods in plasticity, because it has been reported for quasi-static incremental problems that accelerated proximal gradient methods outperform conventional optimizationbased approaches, especially for large-scale problems [17-19].

Acknowledgments

The work described in this paper was partially supported by JSPS KAKENHI (Grant 17K06633) and JST CREST (Grant JPMJCR1911).