一类Duffing 型系统的不动点混沌和Fold/Fold 簇发现象及机理分析1)

陈娅昵 孟文静 钱有华

(浙江师范大学数学与计算机科学学院，浙江金华 321004)

引言

在非线性动力学中有一类问题中有一些参数随着时间的推移而缓慢变化，造成了在同一个系统中存在两个或两个以上的时间尺度，这也被称为多时间尺度问题[1-3].多时间尺度问题具有广泛的应用背景，包括生物网络系统中的神经放电模式[4]、金属氧化反应等.但由于其复杂性，很难用准静态解、奇异摄动法等来研究其解析解，一般只能得到近似的数值解，因此数值分析的方法应运而生.通过数值模拟发现多时间尺度相比于单一的时间尺度具有更复杂的系统表现，如混合模式振荡[5-10].

混合模振荡又称簇发振荡，是一种复杂的振荡模式，它的特征是小振幅振荡和大振幅振荡的结合，可以用快速和缓慢的子系统来描述.当系统处于小幅度振荡时，系统表现出静息状态；当系统经过相关分岔点时会突然失去平衡，进入大幅度振荡，此时系统表现出活跃态.随着慢变量的引导，系统又会从不平衡走向平衡，由活跃态走向静息态，振幅也从大幅度的振荡变为小幅度的振荡，而一旦达到分岔点时，会类似地出现之前的现象.此时的系统就是在静息态和活跃态之间不停地跳跃，称为混合模式振荡.

混合模式振荡也会出现在快慢耦合系统中.Rinzel[11]提出了利用冻结子系统的方法来解释混合模式振荡的想法，这就是我们所知道的快慢分析，它的应用取得了很大的效果.在Izikevich[12]的工作中，创建了混合模式振荡的分类.在快速慢分析的基础上，在研究多时间尺度的系统中，众多学者研究了快慢系统中混合模式振荡出现的机理.例如：Qian 等[13]研究了含两个慢变量的耦合系统的混合振荡模式，讨论了不同时间尺度下的系统动力学行为以及时滞对系统行为的影响；Qian 等[14]研究了单参数激励和双参数激励下的两自由度非线性耦合的Duffing 方程，利用快慢分析方法对耦合系统进行离散，通过数值模拟发现系统会产生簇发振荡现象，并讨论了相关的振动动力学行为；Han 等[8]使用缓慢参数和外部激励来模拟两个缓慢变化的周期参数，并研究了不同时间尺度下的动态响应问题；Zhang 等[15]使用双稳态不对称复合材料层合板对两个慢参数激励的系统以及动态跳跃现象进行了实验和理论分析，提出了一种利用时变原理曲率描述双稳态非对称层合板动态切换现象的新方法；Chen 等[16]展现了具有周期激励的耦合振荡器的弛豫振荡，以典型分叉模式为例，讨论了外激励变化对动态响应的影响，在静止状态和重复尖峰振荡之间交替可以得到簇发振荡；Li 等[17]在具有缓慢周期性参数激励的Duffing 振荡器中，通过数值模拟发现了一种称为周期混沌运动的新型响应，称为不动点混沌；Lin 等[18]研究了一种简单的三元记忆电路周期簇发振荡的分岔机理；Wang 等[19]也研究了简单的自主记忆电路，分析了其对称性、耗散性和平衡稳定性.苟向锋等[20]基于参数平面的耦合研究了单自由度齿轮传动系统安全盆侵蚀与分岔；毕勤胜等[21-22]讨论了不同系统的簇发振荡及其分岔行为；张正娣等[23-24]对于几类非光滑的系统进行了簇发振荡分析；Han 等[25-26]对Duffing 系统进行研究，发现了时滞周转引起的新的簇发振荡类型，叉式翻转迟滞簇发振荡以及复合叉式迟滞簇发振荡.

本文通过构造参数空间来解释簇发现象产生的机理.下面简述这一理论的发展过程.

Rinzel 等[11,27]是第一个利用“解剖”方法来研究快慢系统的簇发振荡，他认为簇发振荡取决于所遇到的分岔，即通过研究慢变量经历不同分岔时产生的跃迁可以对簇发振荡行为进行分类.1995 年，Bertram 等[28]研究了Chay-Cook 模型的两参数分岔图，他们发现这可以看成是三参数焦点型退化Takens-Bogdanov 奇点展开的一个切片.2000 年，Izhikevich[12]发现簇发振荡开始和偏移时的不同位置会导致动态响应发生质的变化.并且基于起始/偏移分岔对来编译可能的簇发振荡分类法.2008 年，Stern 等[29]发现其中一种亚临界Hopf 簇发振荡，它不在余维三奇点展开中出现.2016 年，Osinga 等[30]，研究了生物学和数学的交叉流：伪高原簇发的余维.在一个立方Li´enard 系统的分岔中，发现Fold/homoclinic 簇发振荡与Fold/subHopf 簇发振荡具有非常相似的潜在分岔图，但它不是余维三的，因此可以预测具有余维四.最后通过展示了一个双退化的Bodganov-Takens 点的部分展开中识别出一个三维切片，并证明这个余维四奇异性导致了几乎所有已知的簇发振荡类型.2017 年，Saggio 等[31]提出几乎可以产生所有种类的簇发振荡模型，模型包含两个子系统，对于快子系统，可使用高余维奇点平面展开.在分岔图中，可以确定簇发振荡所需穿过正确分岔序列的路径.而慢子系统沿路径来回引导快子系统.

本文在文献[15]的基础上，针对一类含有两个慢变量的系统使用数值模拟的方法研究了在参数较大的情况下产生的分岔.本文使用数值模拟和基于参数空间的理论分析研究了在参数较小的情况下系统存在双稳态和Fold/Fold 簇发振荡现象，并为控制该系统得到簇发振荡现象提供了参考数据.其中对参数大小的界定标准如下：以1 为界，若参数大于1，认为它是较大的；小于1，则认为它是较小的.

1 不动点混沌

在这一部分我们主要分析了一类含有两个慢变量的Duffing 系统在参数较大情况下的动力学行为.通过数值模拟，得到了系统的时间历程图和相位图.研究表明系统存在不动点混沌，并且随着参数的变化，不动点混沌会表现为单支存在或者双支合并形式.之后本文进一步解释了系统不动点混沌产生的机理.

考虑如下系统

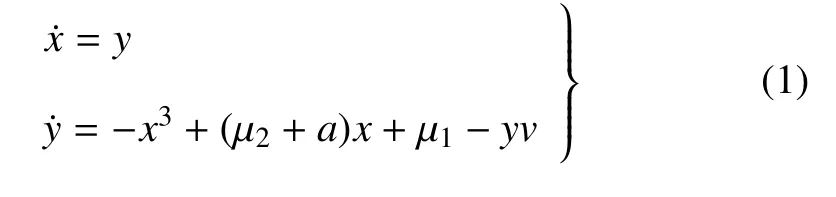
其中，μ1=β1cos(ω1t),μ2=β2cos(ω2t).β1,β2表示振幅，v表示阻尼系数，ω1,ω2表示频率，v,β1,β2被认为是扰动参量.文献[15]对该系统在实验上发现了双稳态现象，并从理论上解释了双稳态现象及动态跳跃现象.

首先假设a=0，则系统(1)变为

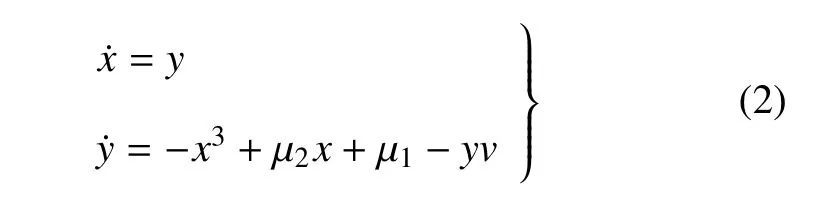
对于系统(2)，为不失一般性，选择β1,β2＞0 并假设ω1=ω2=ω.由于刚度和外激励项是周期性时变的，因此它在一个半周期是正的，在另一个半周期是负的.由于刚度和外激励项的周期性时变性，导致系统产生高度复杂和不寻常的动态响应，包括周期混沌运动的新现象.

固定β1=0.1，β2=6.257 5，v=0.3 时，当ω=0.7 和ω=0.135 5 时，混沌吸引子存在，如图1 和图2 所示.

文献[17]介绍了不动点混沌，这是一种新的混沌现象.它的典型特点是存在一个不动点.对于ω ≪1，系统具有两个不同的时间尺度，一个是快时间尺度，一个是慢时间尺度.当ω=0.135 5，β1=0.1，β2=3.3，v=0.3 时，两个混沌吸引子共存.这些吸引子的最大Lyapunov 指数是正的，表明它们确实是混沌的.而当β2改变时，两个共存的吸引子会分开，出现单独左支或者单独右支的情况.下面保持其他参数不变，而只改变β2分别为2.0 和2.7.

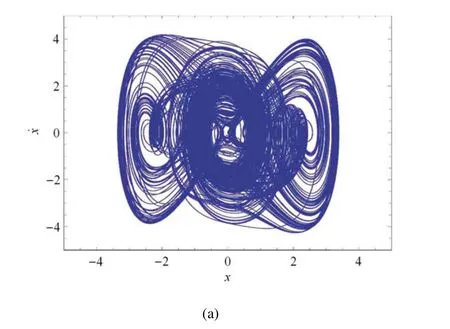
图1 β1=0.1,β2=6.257 5,v=0.3，当ω 分别取0.7 和0.135 5 时系统(2)表现出混沌吸引子Fig.1 β1=0.1,β2=6.257 5,v=0.3，system(2)shows chaotic attractors when ω=0.7 and ω=0.135 5,respectively

图1 β1=0.1,β2=6.257 5,v=0.3，当ω 分别取0.7 和0.135 5 时系统(2)表现出混沌吸引子(续)Fig.1 β1=0.1,β2=6.257 5,v=0.3，system(2)shows chaotic attractors when ω=0.7 and ω=0.135 5,respectively(continued)

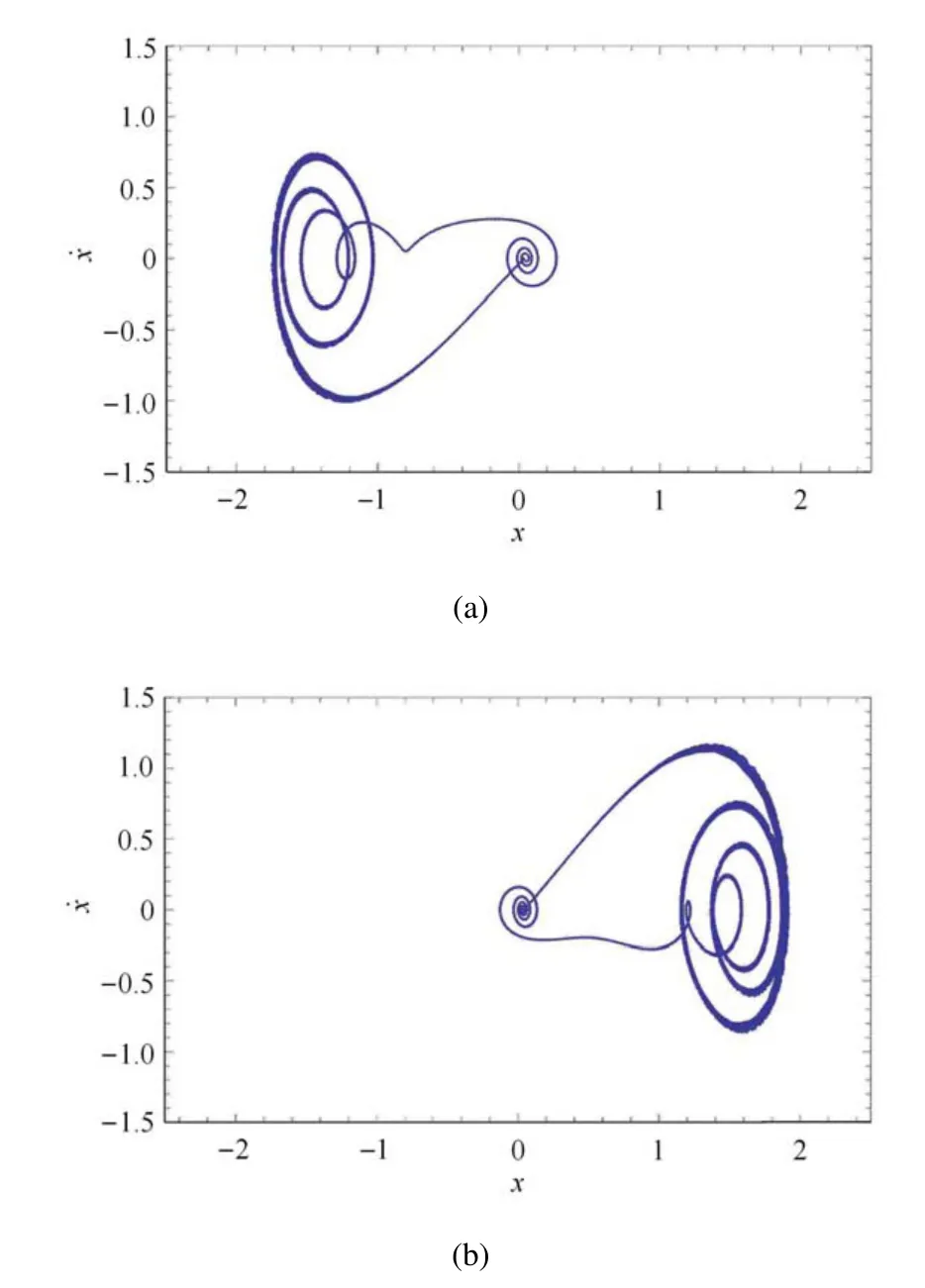
图2 ω=0.1355,β1=0.1,v=0.3，系统(2)在β2=2.0 时表现出单独左支行为，在β2=2.7 时表现出单独右支行为Fig.2 ω=0.1355,β1=0.1,v=0.3，system(2)shows the behaviors of left branch alone with β2=2.0 and right branch alone with β2=2.7

为进一步研究不动点混沌的机理，讨论了快慢系统的分岔行为.对于ω ≪ 1，周期激励μ1=β1cos(ωt)，μ2=β2cos(ωt)分别在[-β1,β1]和[-β2,β2]之间变化缓慢.将μ1,μ2近似地视为一个常数，并将cos(ωt)用作自治系统的分岔参数.

系统(2)的静态平衡解满足

当cos(ωt) ＜ 0 时，系统只有一个稳定平衡点；当cos(ωt) ＞0 时，平衡解由于发生分岔而失稳，产生了一对对称稳定的分岔解，；因此pitchfork 分岔发生在cos(ωt)=0，记为PF.图3给出了系统的离散分岔图.

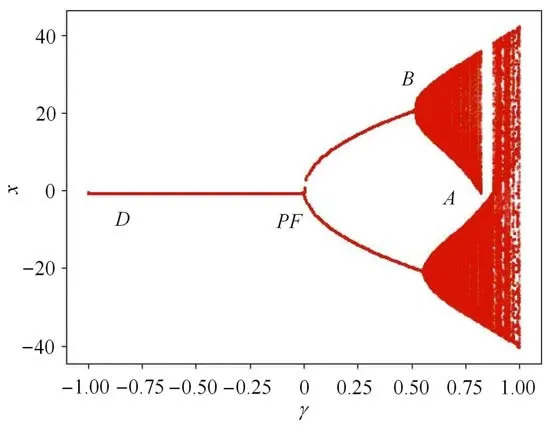
图3 β1=0.1,β2=6.257 5,ω=0.135 5,v=0.3 时系统(2)的离散分岔图Fig.3 Discrete bifurcation diagram of system(2)when β1=0.1,β2=6.257 5,ω=0.135 5,v=0.3

取β1=0.1,β2=6.257 5,ω=0.135 5,v=0.3 来说明不动点混沌机理.图3 显示了规则运动和混沌变化的过程.与上图对应，我们可以看到，A所在的地方是未被红色区域覆盖，此时系统的状态是静默的.在A的右侧，已被红色覆盖，A可以跳跃到上分支或者是下分支，变成了尖峰状态.因此点A是静止状态到尖峰状态的转换点.随着激励的增大，系统在稳定分支的周围拥有尖峰状态.当激励达到最大值，它们开始改变方向，并在同一稳定分支上移动，随着激励的减小而停留在静默状态.当轨迹到达分岔点PF时，它可能被左稳定点吸引，并开始接近稳定平衡点.激励达到最小值，它处于D点.此时，它重新向A点移动，通过平衡点(0，0).然后平衡点(0，0)变得不稳定，逐渐到达B点.在轨迹集合中显示的随机性很可能是因为当系统被吸引到稳定平衡(0，0)时，响应变量x和y是非零的并且很小.在数值计算或实验中，这样的小数字实际上是随机的.因此，离开平衡(0，0)的轨迹在每个周期都有不同的初始条件.对该系统中的初始条件的敏感性显然是混沌的一种性质，所以构成了一个混沌运动.图4 中显示的最大Lyapunov 指数从0.3 变化到小于0.01.它显示了系统丰富的动力学性质，暗示了系统的复杂性.因此，我们对该系统进行了一系列的数值研究.图4 也说明了这一点，当最大Lyapunov 指数大于0 时，表示系统存在混沌现象.

图4 β1=0.1,β2=6.257 5,ω=0.135 5,v=0.3 时系统(2)的最大Lyapunov 指数Fig.4 Maximum lyapunov exponent of system(2)when β1=0.1,β2=6.257 5,ω=0.135 5,v=0.3

2 Fold/Fold 簇发振荡

在这一部分，主要考虑系统(2)中当两个慢变量的振幅β1＜1,β2＜1 时系统簇发振荡现象.系统(2)来源于文献[15].文献[15]从理论和实验两个方面研究了双稳态不对称层合板在外激励的作用下的动态跳跃现象和非线性振动行为，并且发现双稳态不对称层合板在位于中间的不稳定平衡位置时附近会有两个稳定态振动，分别位于上稳定态分支或下稳定态分支.如图5 所示.当系统从一稳定分支跳跃到另一稳定分支时，它就会产生出文献[15]所说的动态跳跃现象，从理论上分析也就是Fold/Fold 簇发振荡.本文对文献[15]中的系统考虑了不同参数的情况.

在快慢系统中，会产生一系列的簇发振荡、尖峰和静止的周期性变化.其中，一个或多个慢变量通过一系列分岔传递快变量，这些分岔介入导致振荡和稳态之间的转换.在以往的研究中发现折叠分岔是余维一的，而两个折叠分岔曲面相交会形成二余维的尖点，如图6 所示.本文通过折叠分岔来解释Fold/Fold 簇发振荡现象.

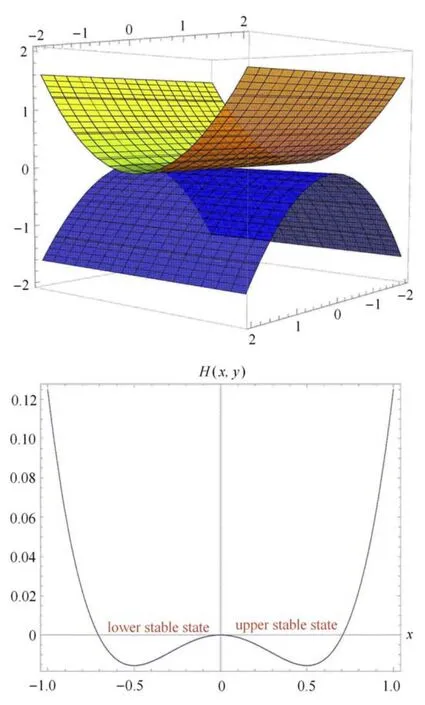
图5 双稳态不对称层合板与动态跳跃现象Fig.5 Bistable unsymmetrical composite square panel and dynamic fracture phenomenon

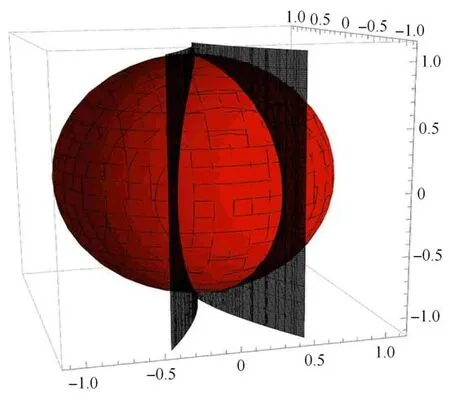
图6 以单位球面为边界的分岔Fig.6 Bifurcation with unit sphere as boundary

此时系统写作快慢系统形式

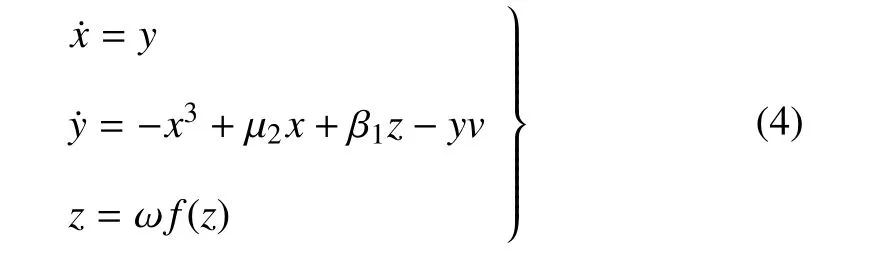
其中

现在将系统视为一个质点，它受到作用在两个垂直方向μ1，μ2轴上的简谐运动，此时这两个分振动可以表示为

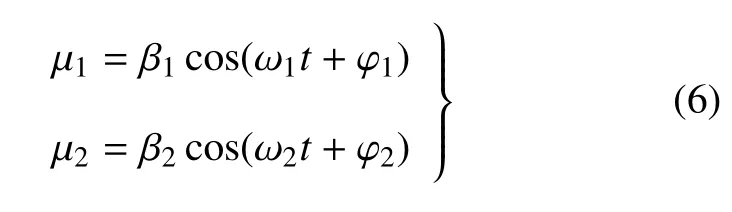
其中，ω1:ω2=1 :2，φ1-φ2=π.可以给出轨迹方程如下

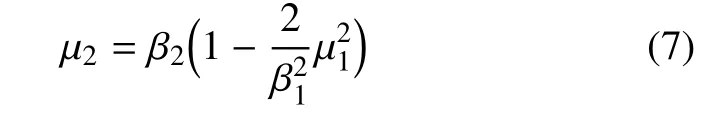
此时任意的β1，β2，a都会产生Fold/Fold 簇发振荡，见图7.下面将详细介绍系统是如何运动的.

在这里可以将相图与时间历程图对应起来解释更微观的情况.图7 显示了簇发振荡，当β1=0.38,ω=0.03,v=0.1 时系统发生Fold/Fold 簇发振荡，在这里可以发现，吸引子在两个平衡点F1，F2附近振荡.F1位于平衡上分支，F2位于平衡下分支.其中的两段尖峰振荡分别对应于平衡点附近，被平衡点F1，F2之间的跳跃运动所连接.在时间历程图上，发现轨迹可以在两个重复的尖峰振荡S P+，S P-之间跳跃，这一运动是对称的.从更深层次的来看，重复尖峰振荡的频率在改变，那是因为相关平衡点在平衡分支上的位置变化，造成了特征值的变化，使得S P±随着慢变参量ω 的变化而变化.

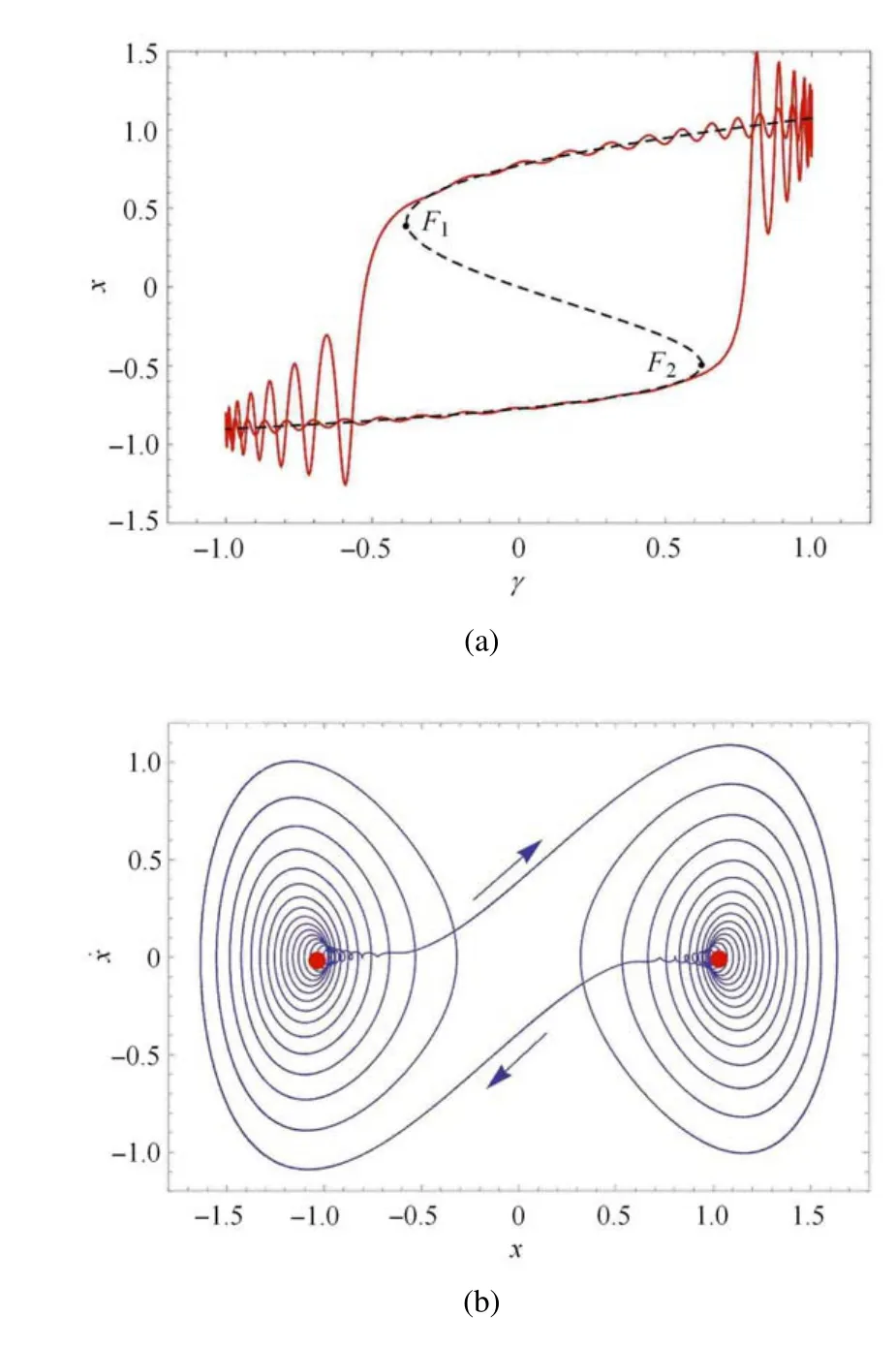
图7 Fold/Fold簇发振荡的叠加图、相图和时间历程图Fig.7 Composition diagram,phase diagram and time history diagram of Fold/Fold bursting

文献[16]表示重复尖峰状态可能围绕F1振荡，平衡点可能从一种状态转变为另一种状态，尖峰行为可以主要由具有较小实部的相关特征值来决定.

假设系统从下分支上的某一点开始运动，它沿着S 型曲线缓慢向右侧移动，直到到达折叠点，它突然从下分支跳跃到上分支，并且围绕上平衡分支F1开始大幅振荡，表现为S P+.随着慢变参数的增大，振荡逐渐减弱.直到慢变参数到达1，系统开始反向运动，然后进入弛豫振荡状态，最后进入静息态，随着慢变参数的不断减小，系统到达另一个折叠点，并且在此时从上分支突然跳跃到下分支，开始围绕F2进行大幅振荡，表现为S P-.振荡逐渐减弱，直到慢变参数到达-1，系统开始反向运动，然后进入弛豫振荡状态，最后进入静息态.如此循环.这就构成了一个周期完整的Fold/Fold 簇发振荡.

该簇发振荡的类型可以称为对称周期性Fold/Fold 簇发振荡，因为此时的系统穿过路径曲线的位置是对称的.

然后解释β1,β2,a的任意性不改变系统的动力学行为.使用一条曲线路径，轨迹的形状如图8(a)所示.为了方便观察双稳态现象，对系统进行欧拉离散，得到图8(b).可以看出图8(b)存在两条分支，如果没有Fold/Fold 簇发振荡，离散后的分岔图只会有一条曲线.当a=0 时，它有一个点(0,β2)始终在μ2轴的上方，而规定了β2必须大于0，这也就解释了在0 ＜β1＜1，0 ＜β2＜1 的情况下，无论β1，β2的取值为多少，都不影响Fold/Fold 簇发振荡产生.并且，此时的Fold/Fold 簇发振荡是对称的.

图8 对应的路径与离散分岔图Fig.8 The corresponding path and dispersed bifurcation diagram

其次，考虑a的变化会带来什么影响，此时，鞍结曲面的位置由.路径方程变成为

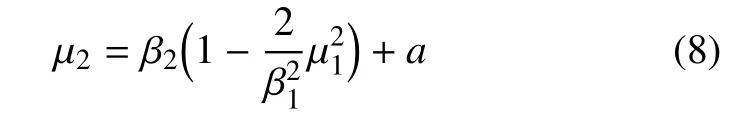
相当于原路径向上平移了a个单位，路径与鞍结曲面必然会相交，只需要保证是在有效范围内相交即可.又由于任意a∈(0,1)都满足0 ＜μ2＜1.这也解释了无论a为何值，在上述的路径下，这并不影响系统从一侧曲面穿到另一侧曲面.更多关于不同频率比与相位差的情况，如表1 所示.

表1 β1=0.38,β2=0.34 三种情况下的分岔图Tabel 1 Three bifurcation diagrams in case of β1=0.38,β2=0.34

3 当a ≠0 时，Fold/Fold 簇发振荡的出现与消失

在上一部分中主要介绍了系统(2)的相关簇发振荡，结合时间历程图、相位图、叠加图仔细地说明了系统是如何运动的.通过参数空间的展开理论和路径说明了系统(2)发生簇发振荡的原因，以及在不同参数下系统的不同行为.在这一部分，介绍新增的常系数项会对系统(1)的动力学行为带来什么影响.先通过数值模拟，发现了一种现象，之后进一步揭示这一现象产生的机理.

考虑当a≠0 时对簇发振荡产生什么影响.固定β1=0.38，ω=0.03，β2=0.80，当a从0.22 变化到0.23 时系统的动力学行为发生巨大的变化.

由图9 可以看出在a=0.22 时，时间历程图表示了簇发振荡的存在，而当a=0.23 时，时间历程图由原来的两段振荡变成了只有上部分的细微振荡，此时簇发振荡已经消失.使用线性路径解释常系数项a的出现却会带来Fold/Fold 簇发振荡.

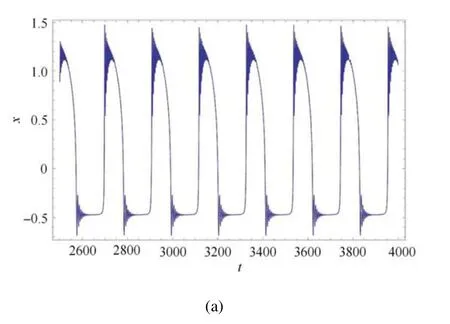
图9 β1=0.38,ω=0.03,β2=0.80,v=0.1，系统(1)的时间历程图当a=0.22 时表现出簇发振荡，当a=0.23 时簇发振荡消失Fig.9 β1=0.38,ω=0.03,β2=0.80,v=0.1,time history diagram of system(1)showing the bursting oscillation with a=0.22 and bursting oscillations disappear with a=0.23

图9 β1=0.38,ω=0.03,β2=0.80,v=0.1，系统(1)的时间历程图当a=0.22 时表现出簇发振荡，当a=0.23 时簇发振荡消失(续)Fig.9 β1=0.38,ω=0.03,β2=0.80,v=0.1,time history diagram of system(1)showing the bursting oscillation with a=0.22 and burstingoscillations disappear with a=0.23(continued)

事实上，若没有常数项，此时路径方程为

此时路径表现为经过原点的线性函数，无论如何，都不会实现从一侧曲面穿越到另一侧曲面.若增加了常系数项，则为从一侧曲面穿越到另一侧曲面提供了可能的路径，仅在二维空间角度考虑，我们有线性路径

当β1=0.38,β2=0.80,a=0.22 时，路径为μ2=2.11μ1+0.22，此时正处于临界状态.路径经过鞍结曲线的一侧，但与另一侧相切，也就是恰好没有经过，此时若控制a＜0.22，路径会穿过左右两侧的曲线，可以实现不对称的Fold/Fold 簇发振荡.

4 多重Fold/Fold 簇发振荡

本节将讨论当μ1=β1cos(nθ)而μ2=β2cos(θ)时会产生什么现象，并且给出了不同现象背后的原因.此时系统变成如下形式

此处，令cos(nθ)=fn(cos θ)，使用结合二项式展开和de Moivre 公式，可以得到

当n=3 时，代入cos(3θ)=4 cos3θ-3 cos θ，可以得到路径方程为

此时的路径关于μ2=a成中心对称.选用不同的参数可以实现该路径与鞍结曲面交点个数的不同，该系统的动力学行为最高可以表现出三重Fold/Fold 簇发振荡.固定β1=0.436,β2=0.327,ω=0.03，v=0.1 通过改变参数a来实现不同重数的Fold/Fold 簇发振荡.a=0.5 的时间历程图、叠加图和路径图如图10 所示.

在图10 中的时间历程图中，阴影部分表示一个周期内的动力学行为，黑色方框表示这个周期内发生Fold/Fold 簇发振荡.可以很明显看出，当a=0.5 时系统发生三次Fold/Fold 簇发振荡.随着a的减小，系统的“1,2,3”振荡会出现不同程度的变化.当a=0.2 时，系统将只发生两次Fold/Fold簇发振荡，与a=0.5 相比，振荡“1,2”的差别不大，但是振荡“3”会明显减弱.当a=-0.1 时，系统的动力学行为会再次改变，与前两者相比，振荡“1”的差别不大，振荡“2”明显减弱，而振荡“3”几乎不显示振荡行为.最后当a=-0.5 时，振荡“1,2,3”几乎都会消失了，此时没有发生Fold/Fold 簇发振荡.其中振荡“3”消失的最为彻底，其次是振荡“2”，振荡“1”还残存着微弱的振荡.

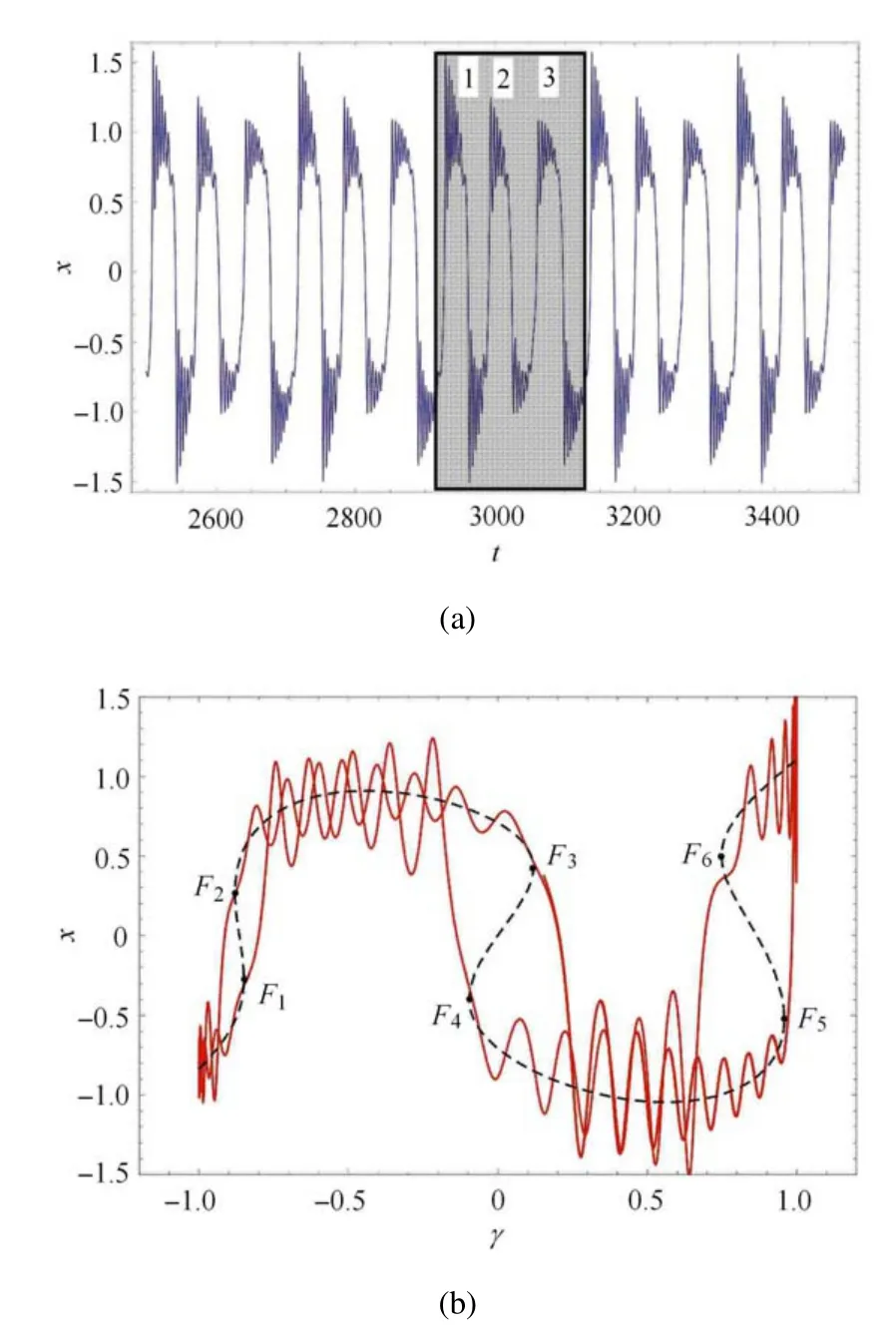
图10 对应的时间历程图、叠加图、路径图Fig.10 Time history diagram,composition diagram and path diagram

图10 对应的时间历程图、叠加图、路径图(续)Fig.10 Time history diagram,composition diagram and path diagram(continued)

这是由于路径最多与鞍结曲面三次相交，即穿过鞍结曲面的两侧.一次相交就对应于一次Fold/Fold 簇发振荡.在a=0.5 时，产生了三次相交，在a=0.2 时，产生了两次相交；a=-0.1 时，产生了一次相交；a=-0.5 时没有相交.

从路径图中可以发现路径与曲面相交的情况复杂多样.表2 表示了不同情况下的Fold/Fold 簇发振荡.

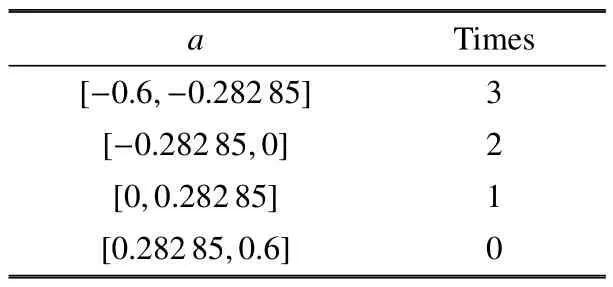
表2 Fold/Fold 簇发振荡重数与a 的关系Tabel 2 The relationship between a and the number of Fold/Fold bursting

关注最大重数在理想的状态下与n之间存在的联系.以n为奇数时为例，结合二项式展开和de Moivre 公式，整理系数可以得到

从该式的固有特点可以看出路径都可以分割成n段，因此理想状态下，如果能使得n段都与鞍结曲面有交点，就可以产生n重Fold/Fold 簇发振荡.

5 结论

系统(1)是一类含有两个慢变量的Duffing型方程，实验研究表明其存在双稳态现象.为了深入理解系统(1)的动力学行为，本文从数值模拟和理论分析两个方面来讨论该系统的混沌特性及簇发振荡行为，得到的结论如下.

(a) 对于系统(2)当振幅参数取值大于1 时，系统表现出了不动点混沌.并且随着参数的变化，不动点混沌可能表现为单支存在或者双支合并.通过叉式分岔解释了当慢变参数小于0 时，系统只有一个稳定解，而当慢变参数大于0 时，系统产生一对稳定的解，随着慢变参数的继续增大，系统出现了混沌.

(b)对于系统(1)来说，它只会产生Fold/Fold 簇发振荡，这是由于它的参数空间中只有鞍结曲面，如果存在其它曲面，对于路径的变化应该十分敏感.并且产生的Fold/Fold 簇发振荡与v的取值无关.对于μ2-μ1型的路径不论是曲线还是线性只要保证它能在有效范围内穿过鞍结曲面的两侧，就能发生Fold/Fold 簇发振荡现象.这能解释第二部分中a,β2选择时的任意性的原因；第三部分中常系数项a的变化使得系统发生巨大改变的原因.值得一提的是穿越鞍结曲面的位置还与Fold/Fold 簇发振荡的对称有关.更多关于不同频率比与相位差的情况，表1 标注了它们是否会得到Fold/Fold 簇发振荡.

(c)当μ1=β1cos(nθ)，μ2=β2cos(θ)时使用μ1-μ2路径讨论产生的现象，此时系统表现出多簇发振荡现象.探究了不同重数的Fold/Fold 簇发振荡与n值之间的关系.由于路径都可以分割成n段，因此理想状态下，n段都会与鞍结曲面有交点，从而产生n重Fold/Fold 簇发振荡.