空间机械臂柔性捕获机构建模与实验研究1)

李海泉 梁建勋 吴爽 刘茜 张文明

*(清华大学航天航空学院,北京 100084)

†(空间智能机器人系统技术与应用北京市重点实验室,北京空间飞行器总体设计部,北京 100094)

引言

空间机械臂是深入开展载人航天活动必不可少的工具,它在空间站系统中承担着舱段捕获与转移、仪器设备转移与安装、辅助航天员作业等功能[1].末端执行器是空间机械臂系统的重要组成部分,安装在机械臂的两端(腕、肩回转关节),能够实现对合作目标的捕获、锁定、电气连接,同时能完成对目标的解锁释放功能.

末端执行器对目标载荷的成功抓捕是空间机械臂完成舱外状态巡检、舱段转位、悬停飞行器捕获等任务的关键.由于平面气浮台试验[2]在约束和操作空间等方面都受到一定的限制,因此为满足机械臂在轨工况全覆盖的验证要求,需要对在轨任务进行一定的仿真模拟,作为气浮式零重力地面二维物理试验和三维半物理试验[3-4]的必要补充.

柔性附件在航天器系统中有着广泛的应用[5-7],得益于大捕获容差的特点[8],末端执行器的绳索式柔性捕获机构被广泛用于国际空间站等航天器的机械臂末端.其理论分析和仿真研究也是近年来国内外学者关注的重点.

介党阳[9]研究了空间大型机械臂末端执行器抓捕控制及载荷运输的轨迹问题,针对载荷运输任务对航天器本体产生的姿态扰动设计了控制算法.丰飞[10]分析了末端执行器的软捕获策略,并着重分析了末端执行器的设计方案和工作原理.潘冬等[11]采用多段刚性微元的形式来模拟柔性绳索的动力学特性,建立了末端执行器柔性捕获机构的动力学模型,并通过气浮实验对比了捕获过程中接触力的变化.Zhang 等[12-13]等采用改进的二维平面绝对节点坐标单元建立了软捕获过程动力学模型,并分析了软捕获过程中接触力的变化以及捕获策略对接触力的影响.荣吉利等[14]采用绝对节点坐标法建立了末端执行器柔性绳索的捕获动力学模型,仿真分析了柔性绳索缠绕漂浮卫星的动力学过程.张龙[15]分析了空间圈套式绳索捕获机构的捕获动力学建模,并分析了捕获过程中的接触碰撞问题.上述研究对末端执行器柔性捕获机构的原理分析和理论建模取得了丰硕的成果.然而,大部分对建模过程和验证方案进行了一定简化,用多段刚性微元代替柔性绳索,或将空间问题简化为平面问题研究,而即使考虑了实际的三维空间构型,在实验验证方面仍然有待补充.

随着理论研究的深入,对柔性绳索的建模研究在近几十年来取得了长足的发展[16],在非线性有限元和连续介质力学理论的支撑下,发展出了几何精确梁理论[17]和绝对节点坐标方法[18]等高效建模理论.随着航天任务对柔性附件需求的发展,相关理论被不断探索与改进[19-24],被应用于多种复杂柔性航天器系统[25-27]、软体机器人[28]及其他大变形问题的动力学仿真与接触碰撞分析中[29-32].相比于多段微元近似的方法,该建模理论的主要优势在于单个单元本身便能够模拟柔性绳索的几何非线性特征,因此对于柔性体,采用少数的单元即可精确的表示出大变形问题,而多段刚性微元则需要几十上百个刚体来模拟一段绳索或其他柔性结构[10].

本文以空间机械臂末端执行器的柔性捕获机构为研究对象,首先采用绝对节点坐标法建立了空间三维柔性捕获机构的动力学模型,充分考虑柔性绳索的大变形特性和绳索与刚性目标之间的接触碰撞问题,推导了软捕获过程的动力学模型.然后建立了地面三维悬吊实验,验证了模型的正确性,最后,将所建立模型与空间机械臂模型进行联合仿真,对舱外状态巡检任务和漂浮目标捕获任务的软捕获阶段进行了仿真预测分析,以期为后续研究和工程发展提供理论基础和相关参考.

1 捕获机构建模

1.1 工作原理

空间机械臂的在轨捕获过程分为3 个阶段[10]:软捕获、拖动和锁定.软捕获阶段又称为柔性预捕获,通过柔性捕获机构在较大的捕获容差范围内将目标适配器上的捕获杆进行缠绕,约束在较小的运动范围内; 拖动阶段通过内部电机运转拉近目标适配器与机械臂末端执行器的距离,拉近过程中通过刚性导向机构进行容差校正,实现目标适配器与末端执行器的完全对齐; 最终通过刚性锁定机构实现机械锁定和电信号连接.其中,软捕获阶段柔性捕获机构的成功操作是后续两阶段的先决条件,并且是解决在轨控制精度带来的大捕获容差和导向机构刚性接触等挑战的关键.

如图1 所示,末端执行器柔性捕获机构由3 根柔性钢丝绳索组成,每根绳索两端分别与转动环和固定环连接,呈3 根空间等距螺旋线分布在末端执行器壳体内部.

固定环与转动环半径相等且圆心同轴,顾名思义,固定环与末端执行器壳体相对固定,转动环由捕获电机通过减速机构驱动,能绕其轴心转动.

初始状态下3 根钢丝绳紧贴固定环和转动环内壁布置,3 根钢丝绳围绕的中间区域为捕获区域;当目标适配器的捕获杆进入捕获区域后,控制系统启动驱动组件,驱动转动环绕其轴心转动,进而牵弓3根钢丝绳运动,钢丝绳所围绕的中间区域逐步变小;直至完成软捕获过程,给出进一步执行信号.

图1 软捕获过程示意图Fig.1 Illustration of the soft capturing process

1.2 柔性绳索建模

本节采用绝对节点坐标法的绳索单元[19]对柔性绳索进行建模,由于实际工程中绳索扭转变形影响较小,该单元考虑了绳索的弯曲变形和拉伸变形,忽略扭转弹性变形的影响.

如图2 所示,为一段柔性绳索,定义单元上一编号为k的节点广义坐标为

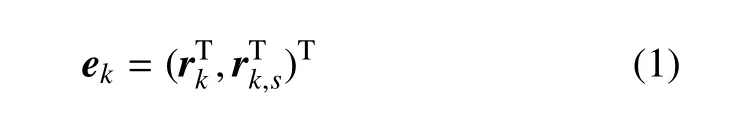
式中,rk表示节点k在全局参考坐标系下的位置坐标值,rk,s=∂rk/∂s,s表示单元轴线方向的弧长坐标,上标T 表示转置.

于是,以节点α 和β 为两端点的任一单元i的广义坐标记为

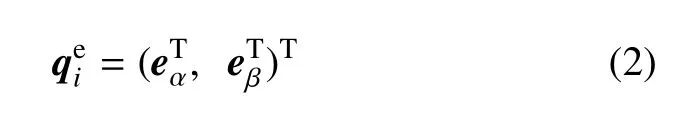
图2 绝对节点坐标法的绳索单元Fig.2 Cable element of ANCF

为便于书写,下文中组集动力学方程内容之前暂时省略单元下标i.该单元上任一点的广义坐标为

式中,S为单元的形函数矩阵

式中,I3为3×3 的单位阵,定义单元长度为le并在弧长方向上进行单位化,即ξ=s/le,则有

对于等截面均质绳索单元,单元的质量矩阵为

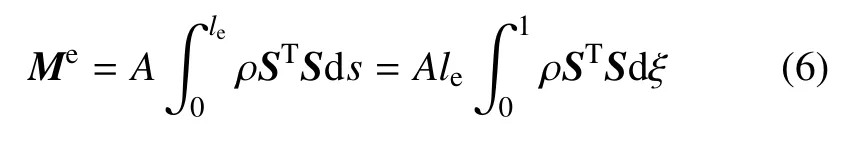
式中,A是绳索横截面的面积,ρ 是材料的密度.

绳索单元的拉伸应变为

弯曲曲率为

于是,绳索单元整体的应变能表示为拉伸应变能Ul和弯曲应变能Ub之和的形式

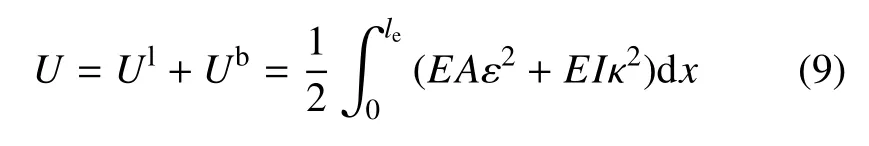
式中,E是绳索材料的弹性模量,I为横截面的惯性矩.进一步,给出绳索单元的弹性拉伸变形力和弯曲变形力

1.3 构型与约束关系

定义捕获坐标系如图3 所示,其中x方向与末端执行器的朝向重合.

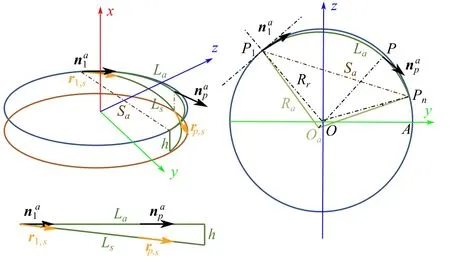
图3 等距螺旋线构型Fig.3 Isometric helices configuration

因此,初始构型下每根绳索在平面yz内的投影都是一段圆弧,该圆弧的弧长和弦长分别为

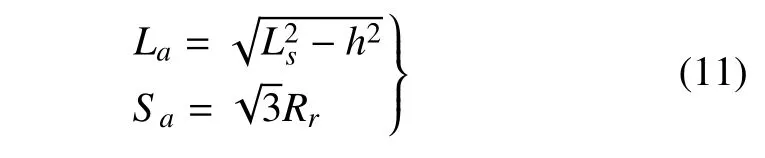
式中,h为两端点在x方向的距离,Ls为单根绳索的长度,Rr是固定环和转动环的半径.

由图3 可得投影的弧长和对应的夹角关系为

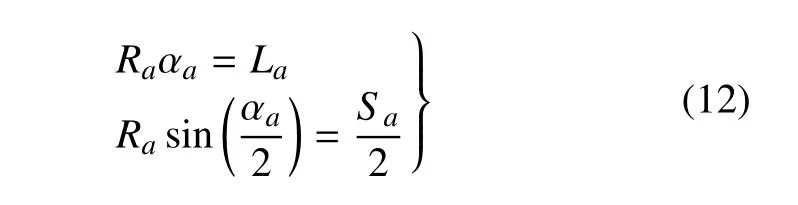
该非线性方程可以采用牛顿迭代法求数值解.如图3所示,∠OaPO=δα=π/3-αa/2,则Oa点的坐标为

式中,α0为绳索初始点连线与Y轴的夹角,对于3 根绳索,分别为2π/3,0 和-2π/3.于是,绳上任一点P的位置为

式中,αp为∠POP1的值,该点的单位切向量值为

从而初始构型下绳索上任一点的广义坐标可以上式确定.

绳索两端分别与固定环和转动环由球铰连接,限制端点处三方向相对位移,于是绳索两端约束方程为

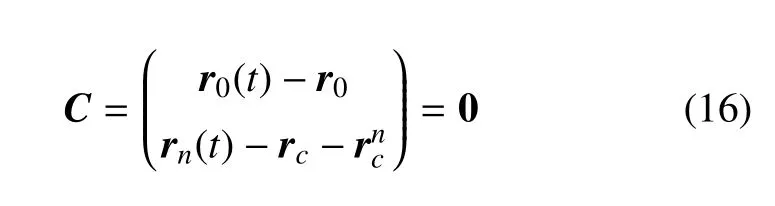
式中,r0(t)与rn(t)分别为绳索两端位置坐标,r0(t)与固定环上r0处相连.圆心Oa到末端点的矢量的坐标阵为

式中,α(t) 为转动环的旋转角度,对于恒定角速度ω的转动,α(t)=ωt.

1.4 接触动力学分析

如图4 所示,在每个单元设置多个接触检测点,任一点P的坐标投影到目标适配器坐标系下,可以写作

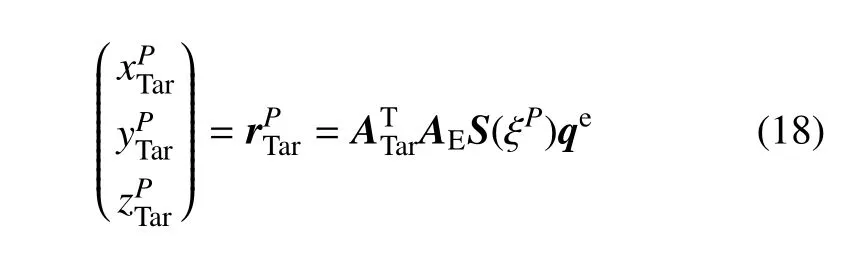
式中,ATar为目标适配器相对于全局坐标系的方向余弦阵,AE为末端执行器相对于全局坐标系的方向余弦阵,ξP为P点归一化后的弧长坐标.

为便于分析,以目标适配器捕获杆中心轴为轴线,弓入一圆柱坐标系如图4(a) 所示,其原点建立在目标适配器坐标系原点,于是P点的坐标值可以用于接触检测,于是接触检测问题转化成了图4(b)所示的一平面问题.此时根据绳索截面圆形与捕获杆剖面的矩形组合体之间接触检测可以判断接触与否以及接触深度.

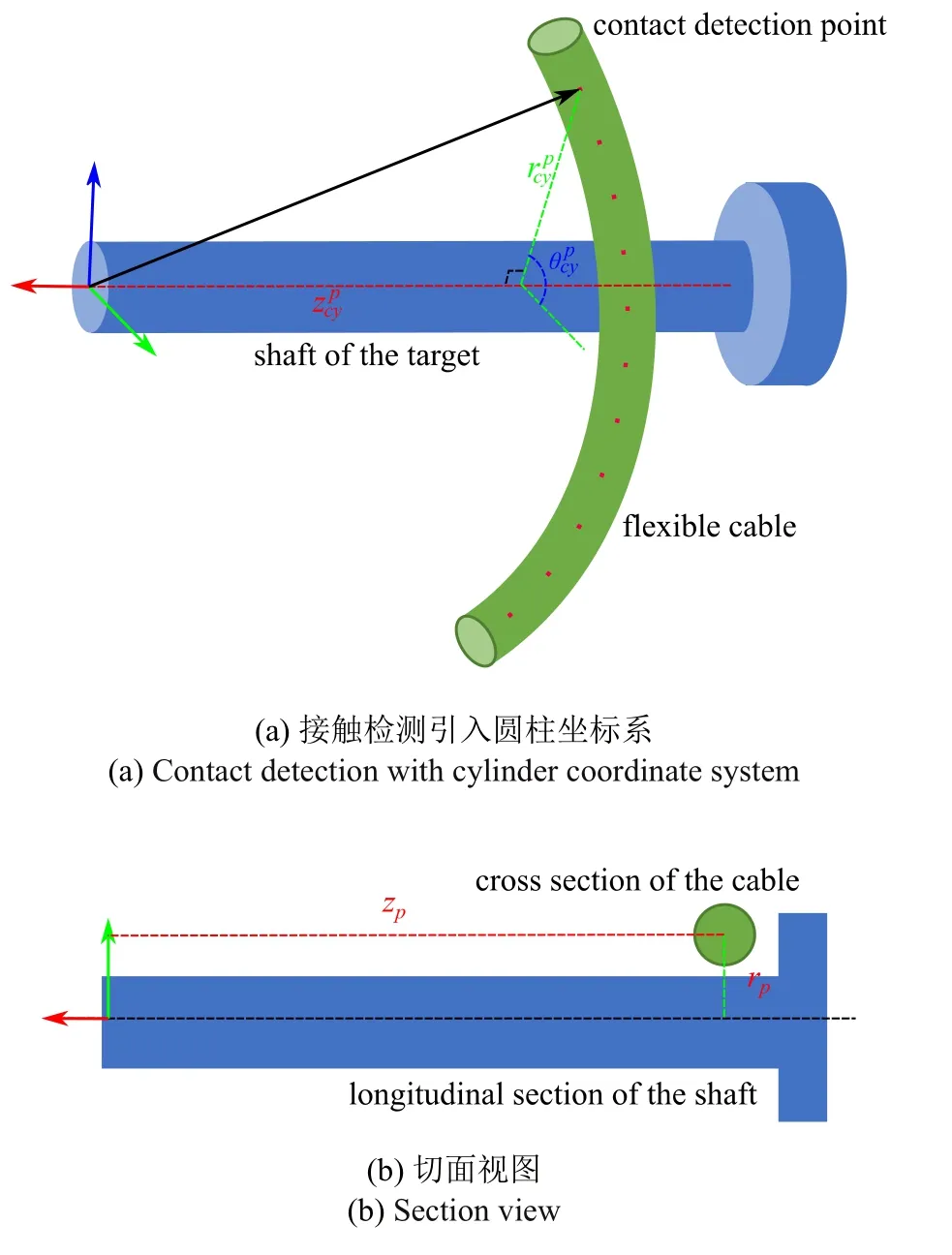
图4 接触检测示意图Fig.4 Contact detection

接触力计算采用赫兹接触碰撞模型[33],由于捕获杆表面光滑度较高,摩擦影响较小,因此采用简单的库伦摩擦模型计算摩擦力

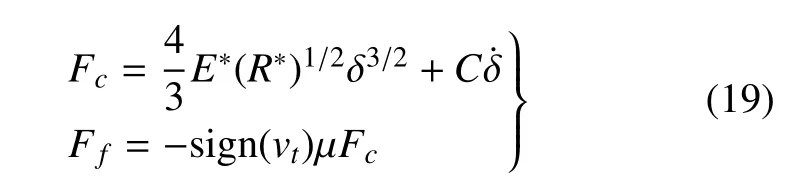
式中,E*为材料接触的等效弹性模量,R*为等效接触半径,δ 为接触嵌入深度,C为接触阻尼系数,vt为接触点的切向相对速度,μ 为库伦摩擦系数.

于是钢丝绳上接触点受力为

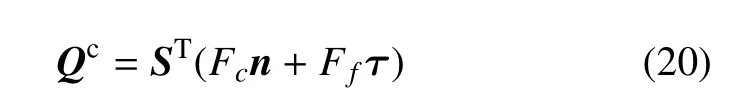
式中,n和τ分别为接触法向与切向单位矢量.

1.5 动力学方程组集

系统中第i个单元坐标与系统广义坐标q的关系可写作

对于矩阵Bi,仅在其第ie列到ie+12 列的位置处取值为12×12 的单位阵,其余位置元素均为0,其中ie为当前单元坐标在系统广义坐标中的起始位置.

组集系统的动力学方程为

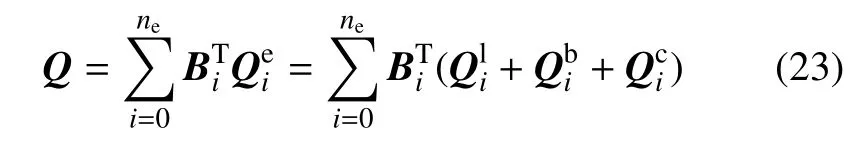
采用数值积分方法对式(22) 求解,可得系统的动力学信息.

2 实验对照

2.1 实验方案

常规的气浮实验只能采集平面二维信息,于是考虑其他方案来进行地面验证.实际在轨抓捕过程中,机械臂关节为被动柔顺状态,整个过程除末端执行器外无其它主动输入.为排除实验过程中主动系统对末端运动的干扰,采用被动弹簧悬吊的方式进行验证.实验场景如图5 所示.

实验过程中力传感器布置于末端执行器根部与实验台连接处,用于采集软捕获过程中的力信号,目标适配器由弹簧悬吊系统悬挂,人为设置初始捕获误差.四周为运动捕捉系统,用于采集捕获过程中的运动信息.

同时建立与实验方案等效的地面悬吊仿真模型,弹簧刚度采用测量值 2042.5 N/m,柔性绳索弹性模量20 GPa,密度7800 kg/m3,每根绳索取10 个绝对节点坐标绳索单元来模拟.初始位置误差设置为x=0.236 9 m,y=0.074 7 m,z=0.040 2 m;初始姿态表示为欧拉四元数[34]的形式,为[0.999 3,0.034 5,-0.007 5,-0.010 8].仿真过程中采用HHT-α 方法[35]进行数值积分,步长1.0×10-5s.软捕获过程转动环角速度为8(°)/s,全程转动80°,软捕获过程持续10 s.

2.2 实验结果及对比分析

图5 实验方案Fig.5 Experiment scheme

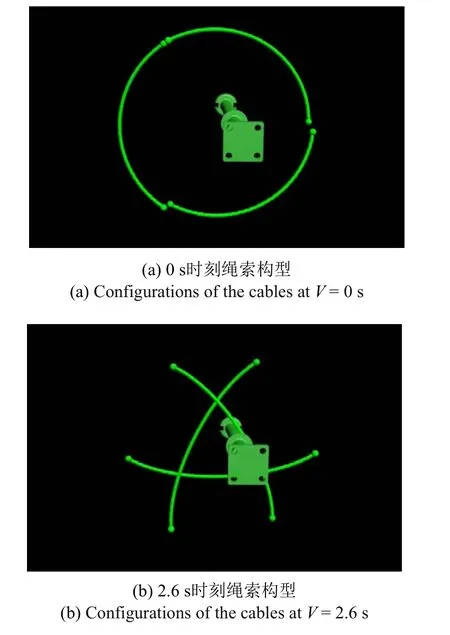
图6 仿真0 s,2.6 s 和10 s 时刻绳索构型Fig.6 Configurations of the three cables at t=0 s,2.6 s and 10 s of the simulation

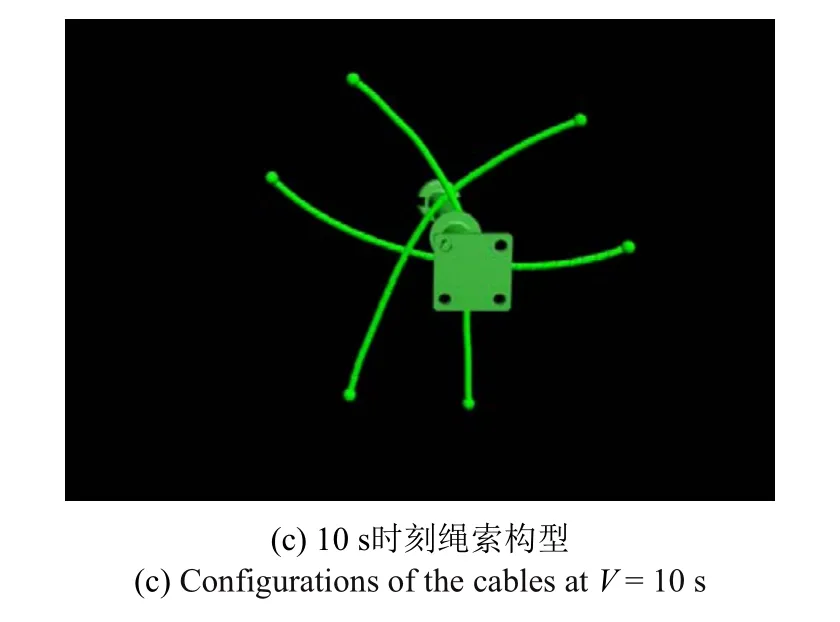
图6 仿真0 s,2.6 s 和10 s 时刻绳索构型(续)Fig.6 Configurations of the three cables at t=0 s,2.6 s and 10 s of the simulation(continued)

图6 为软捕获过程中的仿真画面,分别给出了初始时刻、接触时刻以及软捕获结束时刻的截图.为便于观察,目标适配器仅保留了捕获杆可见,末端执行器仅保留了3 根绳索和端部球铰可见.其中,2.6 s时刻捕获杆初次与钢丝绳发生接触,10 s 时刻钢丝绳收拢到最小范围.

实验结果数据通过坐标变换后转化到末端执行器坐标系下,图7 为实验结果数据与仿真结果的对比.可以看出,仿真结果运动趋势和受力幅值范围基本吻合.

从曲线可以看出,2.6 s 时刻绳索开始与捕获杆发生接触,随着转动环转动,捕获绳索中间围成的区域不断变小,最终收缩至接近中心位置,完成对目标的软捕获,此时目标两径向位移都在1 cm 范围内,已经达到刚性对接机构能够顺利完成后续捕获阶段的范围内.

图7 目标位移和受力仿真与实验对比Fig.7 Comparison of forces act on the target

仿真结果与实验结果三方向位移误差取绝对值后求平均值分别为x方向0.27 mm,y方向2.68 mm和z方向5.99 mm.三方向受力绝对平均误差分别为x方向0.99 N,y方向1.48 N 和z方向2.12 N.仿真结果误差主要来源于测量误差和建模误差,其中,运动捕捉系统和力传感器都存在一定的测量误差,同时运动信息的误差在坐标系转换过程中会对力信息误差产生一定影响.另一方面,由于仿真模型中对悬吊装置进行了简化,未考虑悬吊点的间隙和附加绳索电缆等不确定性因素,因此仿真模型边界条件存在一定误差.

3 任务仿真应用

结合上述模型,对常见在轨任务进行了联合仿真分析,图8 为联合仿真结构框架,其中柔性捕获机构动力学模型、拖动传动机构、刚性对接机构接触动力学模型和控制程序联合组成末端执行器动力学模型,该模型与空间机械臂模型[36]、被捕获目标模型组成任务仿真系统.根据空间机械臂的主要任务设计方案,本文选取了舱外状态巡检(工况1)和悬停飞行器捕获(工况2)两种典型任务[37]下的软捕获动力学仿真过程进行分析.

如图9 所示,舱外状态巡检任务(工况1)中,机械臂肩部末端执行器与漂浮基座相连,通过刚性锁定机构固定在基座上,腕部末端执行器捕获固定在同一基座上另一位置的目标适配器,通过机械臂两端的末端执行器交替抓捕锁定-释放多个布置于基座航天器表面不同位置的目标适配器,实现舱外巡检任务.该过程中目标适配器与基座固定在一起,因此可以以漂浮基座为参考坐标系,将问题等效为固定目标的抓取操作.而悬停飞行器捕获任务(工况2)中,目标与基座各自漂浮,存在相对运动.

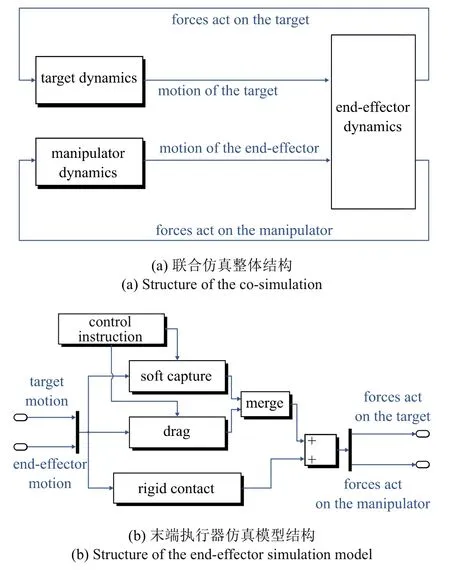
图8 联合仿真示意图Fig.8 Diagram of the co-simulation

图9 在轨操作中两种典型任务Fig.9 Two representative on-orbit operations

抓捕过程中,为避免末端捕获电机的主动控制与关节控制电机输出的力矩互相影响,空间机械臂关节切换为被动柔顺模式,各关节电机停控并释放关节主动力矩,此时各关节仅受关节摩擦与传动机构所产生的被动力矩作用.为便于集中分析末端执行器软捕获阶段的动力学行为,本仿真省略掉机械臂移动过程中的轨迹规划和执行阶段,从末端到位且关节电机停控时刻开始至单次软捕获操作完成时刻终止.

其中基座质量40 t,漂浮目标质量10 t.末端执行器参数与2.1 节内容一致,两工况初始位置容差与角度容差均相同,两径向容差均为0.02 m,轴向初始距离0.12 m,角度容差采用欧拉角描述,三方向均为2°.由于软捕获过程主要影响抓捕操作初始阶段捕获杆与末端执行器径向相对位置,因此图10 给出了仿真过程中目标与末端的径向位移.由于工况1 中目标固定,因此主要靠机械臂末端运动向中间靠近,而工况2 中目标与机械臂末端同时发生靠近运动.

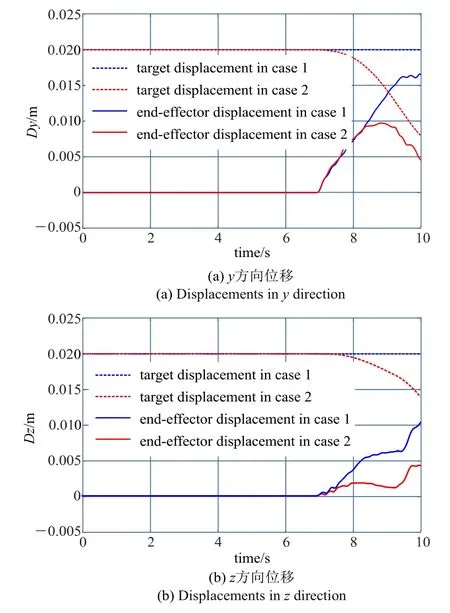
图10 在轨任务仿真结果运动信息Fig.10 Simulation displacement of the two operations

从图10 中可以看出,7 s 左右柔性捕获结构开始与捕获杆发生接触,而后两者相对径向位置逐渐减小,y方向从20 mm 缩减到了最终5 mm 以下,z方向从20 mm 缩减到了最终10 mm 以下.之后较小的容差可以依靠后续拖动过程中的刚性对接机构来完成.

4 结论

本文采用绝对节点坐标法柔性绳索单元建立了空间机械臂末端执行器的软捕获过程动力学模型,针对末端执行器软捕获过程开展了研究,充分考虑了实际工程下的空间构型并建立了绳索与目标捕获杆的接触动力学模型.设计了空间三维的悬吊实验,对所建立的动力学模型进行了验证,证明了模型的准确性.最后,采用所建模型与空间机械臂动力学模型进行联合仿真,对两种空间机械臂任务典型工况进行了分析.研究结果可以为在轨服务研究和工程实践提供一定的参考价值和理论基础.