具有刚性间隙约束输流管的碰撞振动1)

王乙坤 王 琳 倪 樵 杨 沫 刘德政 秦 涛

*(湖北文理学院机械工程学院，湖北襄阳 441053)

†(华中科技大学力学系，武汉 430074)

引言

输流管的振动与可靠性一直是核工业、航空航天和石油化工等行业密切关注的重要工程问题.输流管也被认为是最简单的流固耦合系统,在流体的激励下管道可发生丰富的流致振动现象[1-4].为了提高系统的稳定性,通常会在管道某些位置安装弹性或刚性约束;在长时间服役后,管道振动可能导致约束发生松动,从而在管道和约束之间形成间隙.在某些情形下,因技术需求或装配需要,管道与约束之间可能还预留了一定的间隙.当管道振动的位移达到间隙约束边缘时,二者就会发生碰撞.这种非线性碰撞可能降低管道系统的可靠性,大幅缩短结构的使用寿命.现有关于输流管碰撞振动的研究工作均采用非线性弹簧力来近似描述这种间隙约束力,只能用于模拟管道与间隙之间的柔性碰撞,无法真实地描述刚性碰撞振动的非光滑特征.因此,很有必要针对输流管的非光滑碰撞振动开展相应的研究工作.

Paidoussis 教授是输流管动力学领域的集大成者,早期在输流管数学模型的建立和稳定性问题上做了大量开创性的工作[5-7],在具有间隙约束管道的弹性碰撞振动问题上也有较多突破性的研究成果[8-10].Paidoussis 教授先后提出了立方非线性弹簧和修正的三线性弹簧来描述管道与间隙约束之间的碰撞力,他的研究结果表明这两类模型在管道的柔性碰撞振动方面具有较好的适应性,且理论解和实验结果在定性上吻合较好[8,11].Sadath 等[12]基于立方非线性弹簧和分段三线性弹簧计算了横向流激励下具有多处松动约束悬臂输流管的非线性碰撞振动行为,分析了弹簧刚度对管道振动分岔行为的影响,揭示了系统经由分岔通往混沌的路径.Hassan 等[13]提出了一种能描述管道与约束接触长度和形态的碰撞力模型,可更真实地描述单点接触时管道与约束之间碰撞力的分布情况.Hassan 等[14-15]利用线性弹簧和阻尼器建立了U型管与支撑板的碰撞模型,分析了管道发生流体弹性失稳时的碰撞振动响应,探讨了约束间隙对碰撞力和接触率的影响规律.Azizian[16]系统地研究了输流管与多种约束模型之间的接触形式,考虑碰撞中摩擦力的影响,根据实验测试和工程经验提出了一种能更准确描述碰撞约束力的模型.张艳雷等[17]分析了脉动内流激励下悬臂输流管在立方非线性弹簧约束下的分岔行为和混沌运动,表明大的柔性变形系数可以消除随流速变化的混沌区域；在不同流速下，振荡频率的分岔情况会有复杂的间歇性混沌的发生.王乙坤等[18]分析了悬臂输流管与松动约束发生三维碰撞振动的平面和非平面运动,研究结果表明在平行板约束下管道可出现直线型、椭圆型和瞬变型3 种运动形态[19-20].Geng 等[21]采用基于赫兹接触力模型的碰撞阻尼器分析了悬臂梁发生多模态共振时共振峰和共振幅值随碰撞参数的变化规律,发现大质量的碰撞球能较好地抑制悬臂梁的多模态共振现象,而碰撞间隙的影响则与各阶模态有关,且存在一个抑制多模态共振的最优间隙值.

上述关于输流管的碰撞振动研究均是基于非线性弹簧力的光滑性碰撞模型.由于碰撞过程中弹簧要经历压缩和释放的过程,故这类碰撞力随时间是连续变化的,反映的是光滑性的作用过程.碰撞是一种常见的强非线性现象,碰撞前后存在某些状态向量(如位移、速度和加速度等)的突变使系统的响应曲线存在间断点.因此,刚硬结构之间的碰撞则是一种典型的非光滑现象[22-26].罗冠炜和谢建华[27-28]从非光滑的角度研究了有限自由度碰振系统的周期运动和分岔现象,给出了碰振系统周期解的存在性和稳定性的一般分析方法.Yue 等[29]从理论上分析了两自由度碰振系统的Pitchfork 分岔和Hopf 分岔,给出了碰撞振动的Poincare 映射,揭示了对称和反对称不动点的演化路径.Li 等[30-31]探讨了两自由度碰振系统的周期运动和分岔规律,并计算了相应的Lyapunov 指数,给出了系统在某参数下会出现混沌运动的理论依据.在连续体系统的碰撞振动方面,Wagg 等[32]建立了悬臂梁与单点约束的非光滑碰撞振动模型,运用Galerkin 离散,构造系统的碰撞恢复系数矩阵,推导了梁单元在碰撞前后速度的传递规律,其理论预测与实验结果在定性上具有较好的一致性.

本文将针对脉动内流激励下简支输流管与刚性间隙约束的碰撞振动问题,提出其非光滑动力学数学模型,依据碰撞判别条件和碰撞恢复系数来构建输流管与刚性约束发生碰撞前后速度和位移的传递矩阵;在此基础上,重点分析管道的刚性碰撞振动响应行为,并探究刚性间隙约束参数对输流管碰振行为的影响机制.

1 数学模型

1.1 输流管理论模型

考虑如图1 所示的简支输流管的刚性间隙约束模型.当横向位移较大时，固定在弹性管道中点的刚性套环(蓝色)与刚性约束(红色)会发生刚性碰撞.本文主要探讨管道与刚性约束的正碰撞问题，因此管道被限制在wox平面内运动.图1(a)为管道未变形的初始状态，图1(b)为管道与约束发生碰撞接触的示意图.图1 中x为沿管道长度方向的位置坐标，w(x,t)为管道的横向振动位移，w0为初始的间隙值.管道原长为L，弯曲刚度为EI，材料黏弹性系数为E*，密度为ρp，外径为do,内径为di，横截面积为A，单位长度的质量为m=ρpA.管内不可压缩流体的密度为ρf，单位长度的质量为M=，流速为U，且随时间做周期性变化.

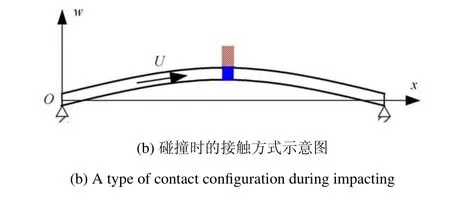
图1 简支输流管单点碰撞振动示意图Fig.1 Schematic of a simply supported pipe subjected to a point impact

根据Euler-Bernoulli 细长梁理论,考虑管道振动时轴线发生变形引起的几何非线性因素,可将脉动内流激励下简支输流管的无量纲振动微分方程描述如下[33-34]

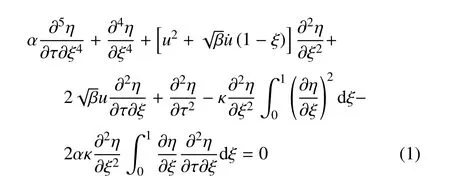
式中,无量纲参数定义为

管内流体的无量纲脉动流速u定义为u=u0(1+σ sin ωτ),其中u0为脉动流的平均流速,σ 为脉动流的脉动幅值,ω 为脉动流的脉动频率.下面采用Galerkin 法对方程(1)进行离散化,即

式中，C为系统的阻尼矩阵,K为刚度矩阵,g()为非线性向量.各矩阵和向量的元素可由下式计算

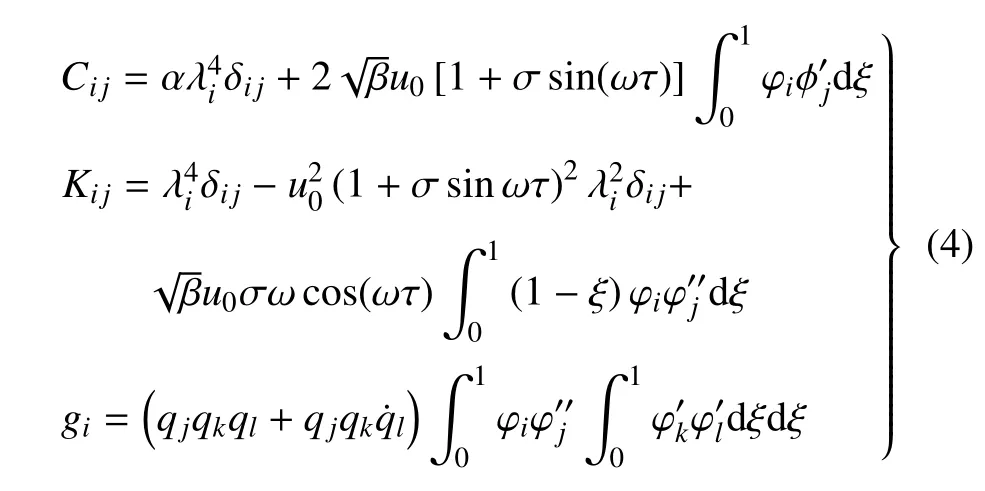
1.2 碰撞传递关系

考虑刚性碰撞的强非线性和瞬时性,本文将忽略管道与刚性约束发生碰撞过程所经历的时间[28,32],故可将碰撞前后管道上各点处节点的位移和速度传递关系写成如下形式

其中,ξb为刚性间隙约束在管道长度方向上的作用位置; τ-表示碰撞前一时刻,τ+表示碰撞后一时刻;r为刚性间隙约束的碰撞恢复系数,用于描述系统非光滑过程的参数.式(5)表示碰撞前后ξ=ξb处碰撞节点的位移和速度传递关系,式(6)表示碰撞前后ξ ≠ ξb处各非碰撞节点的位移和速度关系; 从式(5b)可知,碰撞前后管道在碰撞点的速度存在跳跃间断点,这是一种典型的非光滑现象.

对式(4)进行数值积分时,需将管道划分为P个单元,总节点数为Q=P+1.将这些节点从左到右依次编号为1,2,···,Q.由于间隙约束位于管道中点ξb=1/2 处,为了应用状态向量的传递关系(5)和(6),管道中点处须有一个节点.考虑到所划分节点和单元的对称性,单元数P须为偶数,相应的总节点数Q为奇数,且ξb=1/2 处节点的编号为(Q+1)/2.简支输流管在节点1 和节点Q将应用简支梁的边界条件,则管道上实际发生振动的自由节点数为Q-2,自由节点的编号分别为2,3,···,Q-1.对管道上参与振动的节点分别应用Galerkin 法离散格式(2),可将刚性间隙约束下管道状态向量的关系式(5)和(6)写成如下格式

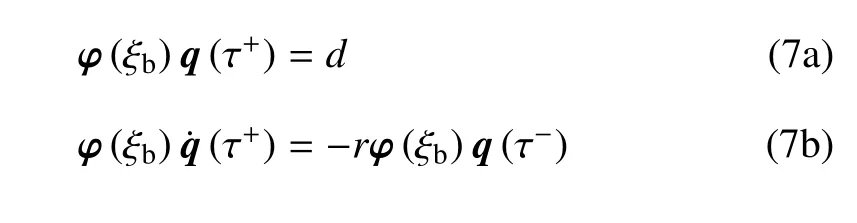
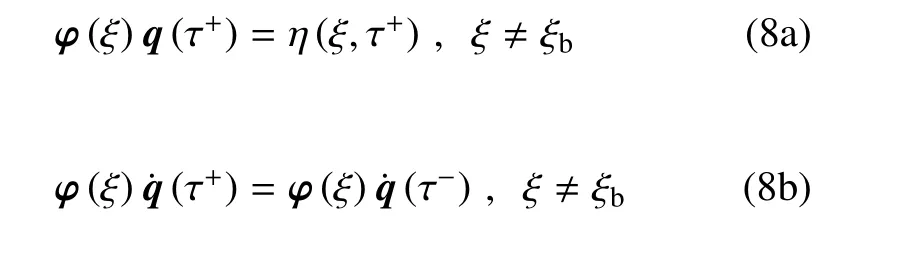
为使碰撞节点ξ=ξb处管道的位移在碰撞瞬间为间隙值d,碰撞后速度变为碰撞前速度的-r倍,且ξ ≠ξb处的单元和节点由于系统的惯性,在管道发生横向振动方向上的位移和速度仍维持碰撞前的状态不变.联立方程(7a)和(8a),并按Galerkin 法展开如下

式中,i=1,2,···,N为模态编号,j=(Q+1)/2 为管道中点的碰撞节点编号.式(9)描述了管道在碰撞前后的广义位移的传递关系,该方程左边系数矩阵由模态函数和自由节点的坐标构成,方程右边表示管道在发生碰撞瞬间各点的位移.方程(9)的解即为碰撞发生后τ+时刻管道的广义位移.式(9)是N元一次线性方程组,其独立方程的数量为Q-2,该方程组有唯一解的条件之一是系数矩阵为方阵,故N=Q-2.令

则碰撞前后管道广义位移的传递关系可改写为

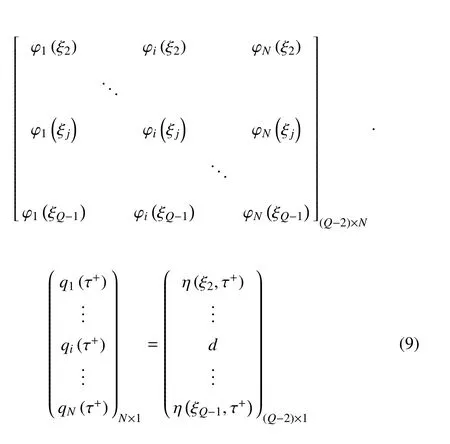
式中,Γ=Φ-1为碰撞前后位移的传递矩阵.为得到碰撞前后广义速度的传递关系,联立方程(7b)和(8b),应用上述N=Q-2 的推论,将这两个方程按Galerkin 法展开如下

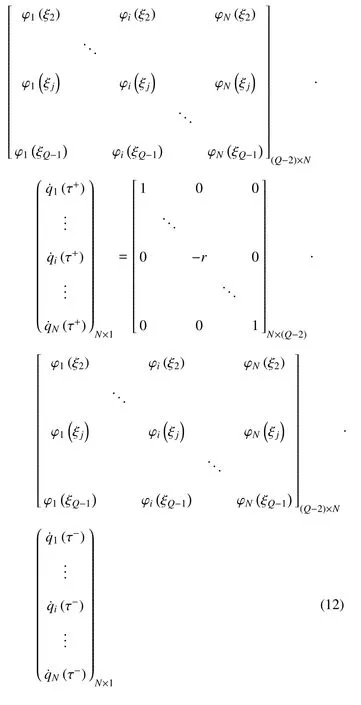
其中,恢复系数r作用在碰撞节点j=(Q+1)/2 处.令

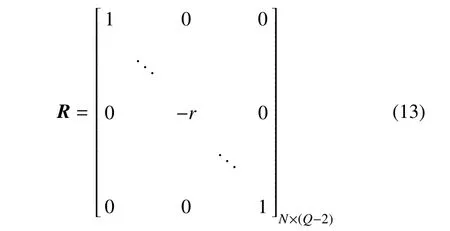
则方程(12)可写成如下形式

式中,Λ=Φ-1RΦ 表示碰撞前后系统速度的传递关系，亦即碰撞恢复系数矩阵.联立式(11)和式(15),运用四阶龙格库塔法对方程(3)进行积分即可得到输流管非光滑碰撞振动的动力学响应.

值得一提的是,本文关于碰撞振动状态向量的传递关系式(11)和式(15)适用于Galerkin 法分析管和梁等结构的非光滑碰撞动力学行为.应用时仅需根据结构的特点(对称、反对称)和约束所在的位置,适当地划分单元,使得间隙约束作用某一节点上,但须满足实际发生振动的自由节点数等于应用Galerkin 法时所取模态截断数的条件.下面将利用式(11)和式(15)研究脉动内流激励下简支输流管与单侧刚性间隙约束的碰撞动力学行为,着重讨论间隙约束参数对管道非线性碰撞振动响应的影响.

2 无间隙约束时输流管的流致振动

为验证本文算法的有效性,并为后文间隙大小的取值提供依据,选取计算参数为:N=5,u=4.5，α=0.005，β=0.64，κ=5000，σ=0.2.经数值计算,得到在没有间隙约束时管道中点无量纲位移随无量纲流速脉动频率的分岔图,如图2 所示.该位移分岔图的计算法则定义为:当管道中点的速度发生反向时,记录速度反向前一时刻的位移.若采用N=2 和σ=0.4 作进一步计算,所得管道的动态响应分岔图与Wang 等[35]的计算结果完全吻合,这表明本文关于无约束两端支承输流管的动态响应问题的算法是正确的.从计算结果来看,在脉动频率约为0 ≤ω ≤55 时,管道位移的最大值约为0.046,且只在极少数脉动频率能达到最大值; 在大部分脉动频率范围内,管道的位移均小于0.038.此外，结合文献[35]的分析结果可知，在4 ＜ω ＜14 频率范围内管道主要表现为复杂的非周期运动.由于两端支承管在定常流速下的失稳方式为静态屈曲，故在更高频率值的范围内管道易出现对称和反对称的周期运动，其分岔图中还可能包含有多周期运动的窗口.

图2 无间隙约束时管道中点位移随流速脉动频率变化的分岔图Fig.2 Bifurcation diagram of the mid-point displacement of the supported pipe without rigid constraint under various pulsating frequencies

在进行Galerkin 法离散化时,若单元数P=2、总节点数Q=3,则系统的自由节点数为Q-2=1,此时两端支承输流管动力学模型可以简化成一个单自由度的碰撞振动系统.本文采用罗冠炜和谢建华等的方法[27]对该单自由度输流管系统进行碰撞振动分析,发现在ω=14，R=0.8 和d=0.035 时管道在双侧对称刚性约束下出现了典型的2/1 碰振响应(图3),这在定性上与文献[27]的结论是一致的,表明本文关于碰撞前后状态向量传递关系的描述是正确的.

3 刚性约束间隙值的影响

从图2 结果可知,当ω=10 时管道的响应处于非周期运动状态,当ω=20 时管道处于周期运动状态.因此,本文选择性地取这两种典型运动状态下的频率值来初步分析约束间隙对管道动力学响应的影响规律.典型的计算结果如图4 所示,其中恢复系数r=0.9.

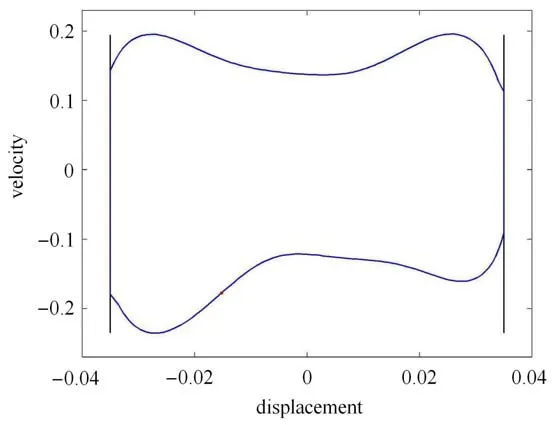
图3 ω=14,R=0.8,d=0.035 时管道单自由度系统的碰撞振动响应Fig.3 Vibro-impact response of a single-degree-of-freedom system of the pipe with ω=14,R=0.8 and d=0.035

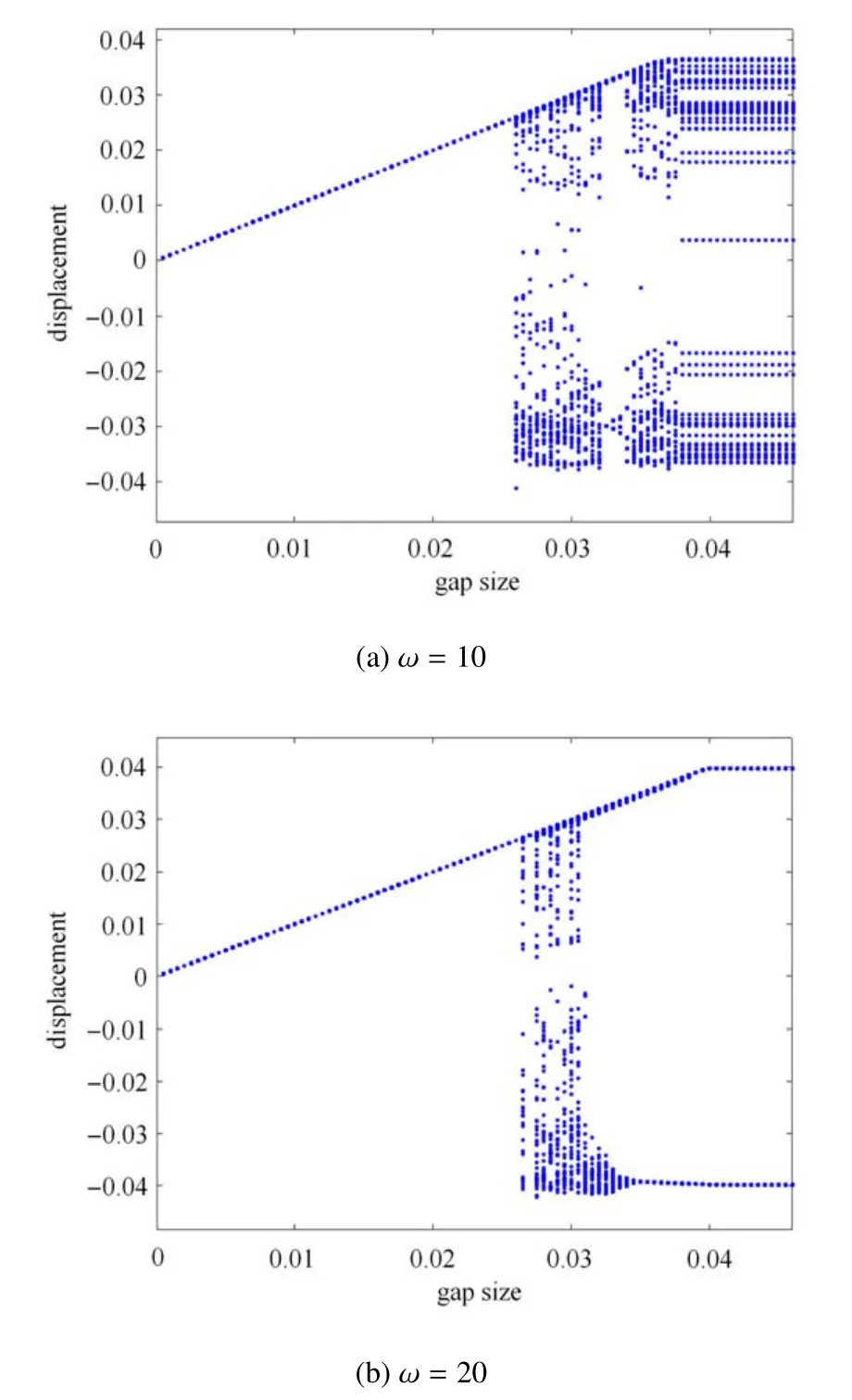
图4 管道中点位移随间隙值变化的分岔图Fig.4 Bifurcation diagrams of the mid-point displacement of the supported pipe under various gap distances

计算结果显示,当ω=10 时,较小的间隙值(0 ≤d≤0.025)会抑制管道原有的振动,此时管道可能粘连在刚性约束上; 随着间隙值的增大(0.026 ≤d≤0.046),管道可发生复杂的振动行为,故在分岔图中显示为密集的散点.当间隙值取为0.038 ≤d≤0.046 范围时,因管道位移最大值约为0.038,故管道与刚性约束之间的碰撞很弱或不再发生接触.当ω=20 时,较小的间隙值如0 ≤d≤0.027 仍可使管道粘贴在刚性约束上而不出现振动; 当间隙值在0.028 ≤d≤0.035 范围时,管道会发生复杂的振动行为,并在更大的间隙值时逐渐演化为周期1 运动形态; 在0.036 ≤d≤0.04 范围内,管道将维持周期1 碰撞振动; 当间隙值继续增大到0.04 ≤d≤0.046 范围时,因间隙值较大,管道将不再与刚性约束发生碰撞.上述列出的各种动力学现象表明,约束间隙值对管道的动态响应行为影响十分明显,较小的约束间隙值可抑制管道的振动,中等大小的间隙值会导致复杂的运动形态,较大的间隙值则不会发生碰撞.

基于图4 的计算结果,选取两个间隙值(d=0.03 和d=0.035)来分析管道的刚性碰撞振动行为随脉动频率的变化情况,以进一步揭示间隙值对管道动力学响应的影响规律.图5 和图6 分别给出了这两种间隙值下管道中点的位移和速度随管内流体脉动频率变化的分岔图.其中,速度分岔图的计算法则为:当管道与约束发生碰撞时η(ξb,τ+)=d,记录碰撞前一时刻的速度˙η(ξb,τ-).从该计算法则可知,速度分岔图主要反映管道与刚性约束间发生碰撞的次数,从而反映出管道与约束的周期和非周期性的碰撞振动行为.

图5 管道中点位移和速度随脉动频率变化的分岔图,d=0.03Fig.5 Bifurcation diagrams of the mid-point displacement and velocity of the supported pipe under various pulsating frequencies,for d=0.03

图6 管道中点位移和速度随脉动频率变化的分岔图,d=0.035Fig.6 Bifurcation diagrams of the mid-point displacement and velocity of the supported pipe under various pulsating frequencies,for d=0.035

从图5 的管道中点位移和速度分岔图可知,d=0.03 时在较宽的脉动频率范围内,即3 ≤ω ≤24.6，35.1 ≤ω ≤40.4，52.1 ≤ω ≤54.4,管道均处于非周期运动状,表现为一种无序的碰撞振动状态;在24.7 ≤ ω ≤ 35 范围里,管道振动行为与无间隙约束时保持一致(见图2),速度分岔图则显示此时管道与约束不发生接触; 在较高脉动频率值区域内(43.8 ≤ ω ≤ 52),管道与间隙约束仍可粘连在一起而不发生振动.不过,在某些较高脉动频率值的参数范围(如40.5 ≤ ω ≤ 43.7)里,管道在一个运动周期内可出现多次碰撞振动的情形.从图6 可发现,当d=0.035 时,管道发生非周期性碰撞振动的频率区间比d=0.03 的要窄,而发生周期性多次碰撞振动的脉动频率范围显著增宽(如15.3 ≤ω ≤20.5 和35.6 ≤ω ≤46.3);当20.6 ≤ω ≤24.6 或46.7 ≤ω ≤49.1 时,管道与约束发生复杂的多次碰撞.从上述关于图5 和图6 的分析可知,若一个振动周期内出现多次碰撞,其碰撞振动次数通常会随着脉动频率的增大而逐渐增多.当运动管道遇到固定的刚性约束时,加速度方向保持不变,碰撞前的速度经由多次碰撞逐渐减小到零(如图6 中20.4 ≤ω ≤24.7的情形),此时管道发生了黏滑运动[36].这种黏滑运动是非光滑系统不同于光滑系统的动力学现象之一.

为了更直观地观察管道在某些脉动频率激励下的动态响应,图7 描绘了4 种不同脉动频率取值时管道振动的相图和Poincare 映射图.其中，Poincare 映射的法则为:每经历一个脉动激励周期,记录当前时刻管道中点的位移和速度.根据Poincare 映射点的分布形态可以判断此时管道的运动状态(如周期,概周期和混沌等).图7(a)和图7(c)分别给出了d=0.03，ω=38 和d=0.035，ω=10 时管道的动态响应,此时的Poincare 映射图为一系列离散点构成且具有分形结构的奇异吸引子,表明此时管道的非周期碰撞振动状态是混沌运动.图7(b)和图7(d)分别显示了d=0.03,ω=43和d=0.035，ω=42 时管道的动态响应,此时管道处于周期1运动状态.从图7(b)的Poincare 映射图可看到5 个映射点,而图7(d)中则只有4 个映射点; 从映射法则可知,映射点的数量代表经历的脉动周期数,故二者是不同类型的周期性碰撞振动.由图5(b)和图6(b)的速度分岔图可知,在这两个脉动频率下,管道与刚性约束均发生了4 次碰撞.由文献[27]可进一步发现,图7(b)是4/5 的周期碰撞振动,而图7(d)是4/4 的周期碰撞振动,这也是非光滑碰振系统特有的现象之一.

图7 管道中点运动的相图(蓝色线)和Poincare 映射(红色点)Fig.7 Phase portrait(blue line)and Poincare map(red point)of the mid-point of the pipe

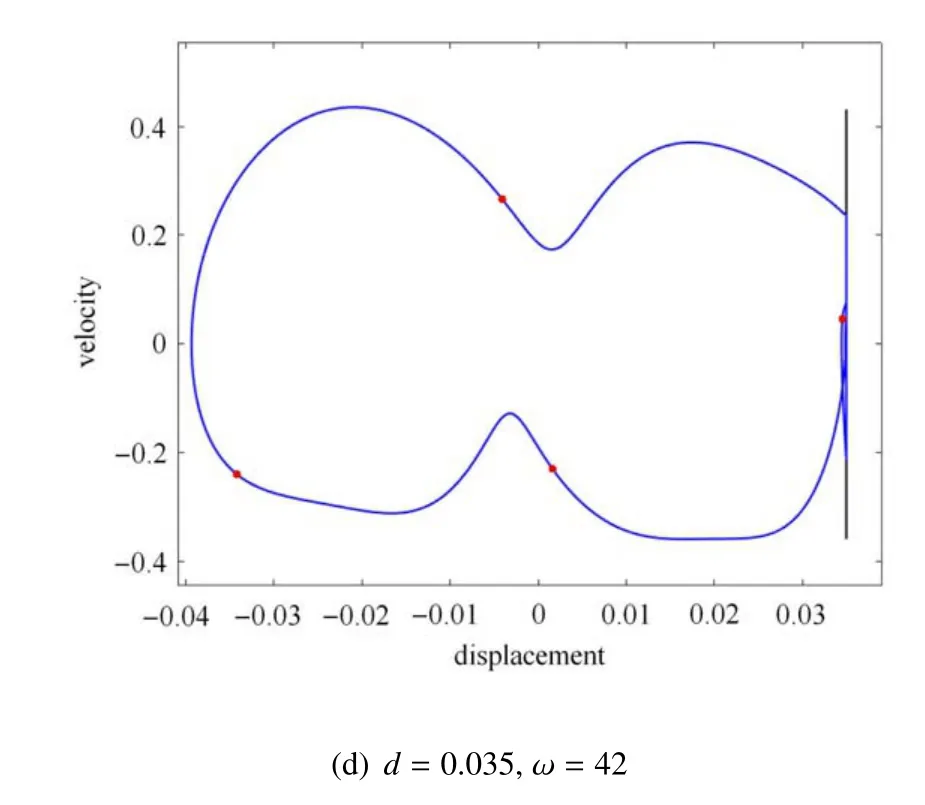
图7 管道中点运动的相图(蓝色线)和Poincare 映射(红色点)(续)Fig.7 Phase portrait(blue line)and Poincare map(red point)of the mid-point of the pipe(continued)

4 碰撞恢复系数的影响

为了探究恢复系数对管道碰撞振动行为的影响,约束间隙值取为d=0.035,其他参数值保持不变.图8 给出了恢复系数r=0.8，r=0.7 和r=0.6 时管道中点位移和速度的响应随脉动频率变化的分岔图.与图6 中r=0.9 的分岔图对比可看出,随着恢复系数的降低,复杂的非周期碰撞振动所对应的脉动频率区间显著增大,周期性碰撞振动的脉动频率范围大幅缩小.由此可见,对本文所研究的碰撞振动系统,较小的恢复系数极大地增加了系统出现不规则碰撞振动现象的可能性,而较大的恢复系数有助于使系统在较宽的频率范围内处于周期性碰撞振动状态,可一定程度上抑制混沌运动的出现.

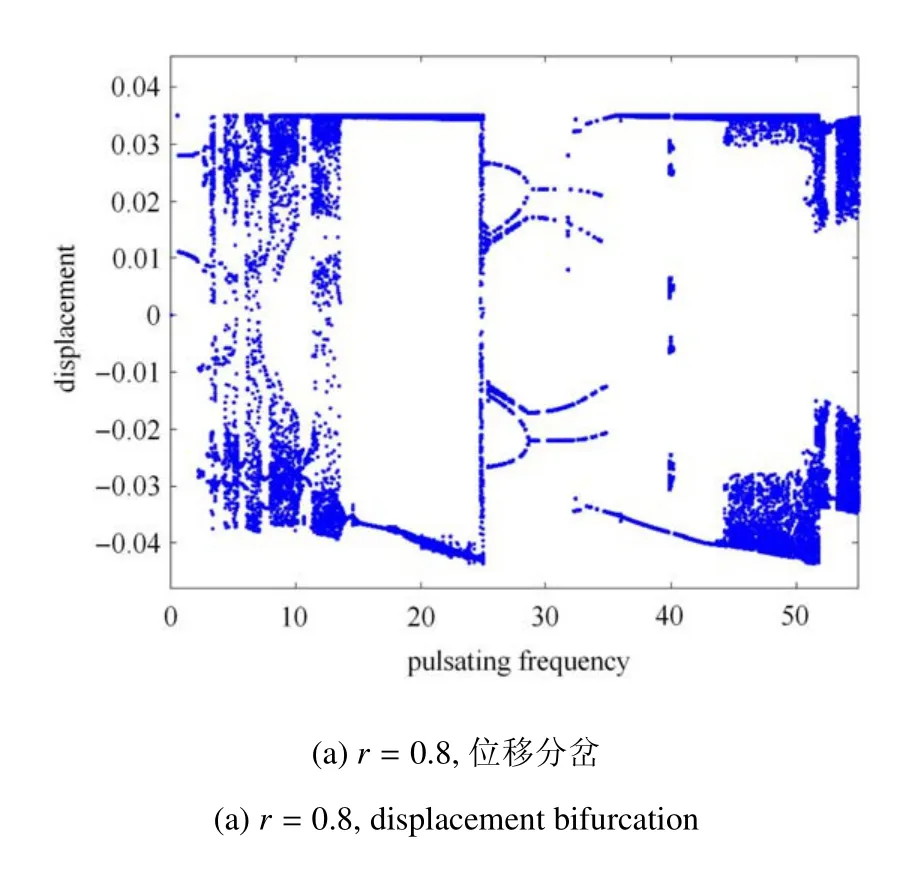
图8 管道中点位移和速度随脉动频率变化的分岔图Fig.8 Bifurcation diagrams of the mid-point displacement and velocity of the supported pipe under various pulsating frequencies

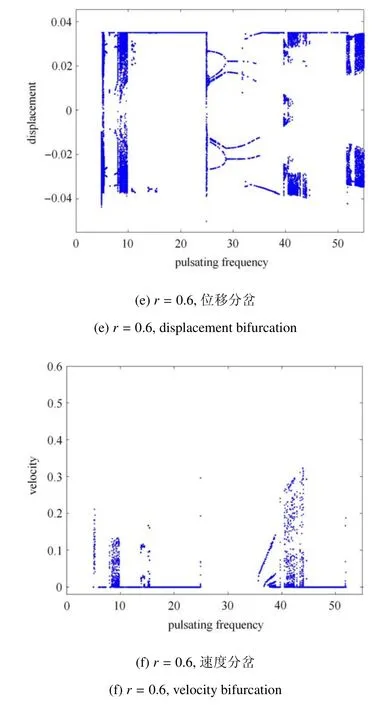
图8 管道中点位移和速度随脉动频率变化的分岔图(续)Fig.8 Bifurcation diagrams of the mid-point displacement and velocity of the supported pipe under various pulsating frequencies(continued)

5 结论

本文基于非光滑理论建立了简支输流管与刚性间隙约束的碰撞振动模型,构造了碰撞前后系统状态向量的传递矩阵,分析了在脉动内流激励下管道与刚性间隙约束的碰撞振动行为,讨论了间隙约束间隙值和碰撞恢复系数对管道动态响应的影响.研究结果表明,较小的约束间隙值会使管道粘连在刚性约束上,即不出现振动;较大的约束间隙值可使管道随流速脉动频率的变化而演化出规律的多周期运动和复杂的非周期碰撞振动; 约束间隙值的大小还会显著影响出现非周期性碰撞振动的流速脉动频率范围.碰撞恢复系数对管道周期和非周期性碰撞振动的影响也十分显著,较高的恢复系数值有利于使管道处于周期性碰撞振动状态,而较小的恢复系数值则容易使系统在更宽的脉动频率范围内出现非周期性的碰撞振动.此外,本文研究工作还观察到输流管刚性碰撞时的黏滑现象,这是有别于以往输流管弹性碰撞振动研究结果的新的非光滑动力学特征.