三维切口/裂纹结构的扩展边界元法分析1)

李 聪 牛忠荣 胡宗军 胡 斌

*(合肥工业大学土木与水利工程学院力学系，合肥 230009)

†(安徽建筑大学土木工程学院，合肥 230601)

引言

在土木、机械和航空等工程结构中经常出现三维V 形切口/裂纹问题，如地下室方形洞室角区、重力坝踵坝趾区等.由于几何形状或材料组成的突变会造成三维V 形切口/裂纹尖端的强应力集中，严重时会导致受力构件甚至结构的整体破坏.因而，准确计算三维V 形切口/裂纹结构的应力场具有重要的理论意义和工程实用意义.

目前国内外学者对于三维V 形切口/裂纹结构的研究大多局限于裂尖场的奇异项、应力强度因子、裂纹扩展路径等.Chue 和Liu[1]给出了正交各向异性切口应力奇异阶的一般解，并指出解的奇异性取决于切口角度、边界条件及材料特性.Ungamornrat[2]用弱奇异对称Galerkin 边界元法(SGBEM)分析了三维多相材料线弹性裂纹结构的应力奇异性.Sator 和Becker[3]采用复变函数法获得了各向同性多材料接头端部应力奇异性指数的解析解.胡宗军等[4]建立了三维位势问题高阶边界单元几乎强奇异和几乎超奇异积分的半解析算法，其数值结果表明该方法可高效计算边界元法中几乎奇异面积分.Wu 等[5]基于离散的快速傅里叶变换(FFT)理论，推导出线弹性各向异性双材料结构的界面应力场的半解析解.

此外，对应力强度因子和裂纹扩展的研究也比较深入.文龙飞等[6]基于改进型扩展有限元法，研究了动载荷作用下扩展裂纹尖端应力强度因子的求解方法.Xu 等[7]在变长径比和双材料参数下，采用体力法计算了三维矩形界面裂纹的应力强度因子.王振和余天堂[8]采用自适应多尺度扩展有限元法计算了三维I 型裂纹和I-II 复合型裂纹的应力强度因子.贾旭等[9]采用裂纹弹性应力场的有限元解计算了三维裂纹的应力强度因子，其结果符合三维裂纹体裂纹尖端实际的应力应变状态.Fakovr 和Ghoreishi[10]研究了机械支柱、转速、裂纹取向等因素对旋转盘中应力强度因子的影响.Huang 等[11]采用有限块法(FBM)计算了静载荷和瞬态动态载荷下的应力强度因子和t应力.贾旭等[12]提出了三维矩形平板内承受复杂非线性载荷下，仅含有3个系数的通用权函数，并采用FEM 计算了三维含穿透裂纹的矩形板的3 组参考应力强度因子.Magnus[13]采用FEM 分析了三维各向异性低渗透岩石在水压作用下的应力场.Dhanesh 等[14]采用迭代分析技术MMEKM 分析了三维弹性复合材料层合板在均匀轴向拉伸、弯曲、扭转和热载荷下的应力场，结果显示了自由边应力场的MMEKM 解在项数和迭代次数方面具有良好的收敛特性.Stasyuk[15]基于改进的边界积分方程法，分析了三维弹性无限体和有限弹性体中两个相互作用的圆盘形裂纹附近三维应力强度因子，并给出了裂纹沿法向均匀加载下的应力场.

Karsten 和Gunther[16]采用对偶边界元法模拟了复杂三维线弹性裂纹的裂纹扩展路径，其结果和实验结果吻合较好.Li 和Guo[17]采用三维FEM 研究了有限厚度板在单轴拉应力作用下的V 形切口尖端弹性应力场，研究结果表明了板厚、切口角度对应力集中系数有明显的影响等.Park 和Nikishkov[18]提出了SGBEM-FEM 交替方法，该方法可有效分析三维平面和非平面裂纹及其扩展.Lan 等[19]采用三维FEM 模拟了铝合金板在混合型加载下的裂纹扩展过程，并研究了裂纹尖端有限元尺寸和裂纹扩展增量尺寸对模拟预测结果的影响.Dias 等[20]采用有限元方法模拟了准脆性材料的三维裂纹扩展问题，该方法可高效模拟位移不连续扩展的性能.Ding 和Wang[21]采用三维边界层(小范围屈服)公式对三维小应变进行了弹塑性模拟，模拟结果表明了尖端区域非奇异T 应力对塑性区的尺寸和形状有显著的影响，且应力的大小、方向也受到T 应力的影响.Wang 等[22]通过建立三维复合材料的2 种几何结构模型：微观结构模型和多单元模型，分析了三维碳/环氧复合材料在-100°C 至-140°C 不同温度场下的热膨胀行为和界面热应力.

研究三维线弹性V 形切口/裂纹的文献很多，但大多局限在研究第1 阶应力奇性指数及其在此基础上模拟裂纹扩展路径，而关于三维切口/裂纹结构完整位移和应力场的分析缺乏有效方法.本文基于二维V 形切口/裂纹结构的全域弹性应力场[23-24]的求解思想，联合尖端扇形柱的渐近分析和外围结构的边界元法分析求解三维V 形切口/裂纹结构完整的位移和应力场，称之为扩展边界元法(XBEM).XBEM 计及了离尖端径向距离r的渐近级数展开式中若干项的特征指数和特征函数.文中将通过算例定量展现XBEM 求解三维V 形切口/裂纹结构完整应力场的准确性和适用性.

1 线弹性三维V 形切口/裂纹尖端附近应力奇异性分析

考虑三维柱状V 形切口结构，如图1 所示，其柱形切口张角为α=2π-θ1-θ2.当α=0°时，图1 所示结构为三维裂纹结构.将三维V 形切口结构分为一个半径r=ρ 的扇形柱体(图2(b))和外围结构(图2(a))两部分.外围结构新形成的边界为，在切口尖端处同时定义笛卡尔坐标系ox1x2x3和柱坐标系orθz(坐标原点o在切口尖端).扇形柱体是应力奇异性区域，外围结构是无应力奇异性的普通弹性区域.对于一个三维V 形切口结构，图2(b)所示切口尖端附近应力奇异性区域的位移场可表达成关于径向r的渐近级数展开式[25-26]

式中，Ak为位移幅值系数，λk为切口尖端的位移特征指数，N表示截取的级数项数，(θ,z,λk)，(θ,z,λk)，(θ,z,λk) 为位移特征角函数.由于图2(b)结构形状沿z方向是相同的，并不涉及外载荷，因此分析切口尖端扇形柱区域的奇异性时，式(1)中的特征角函数(θ,z,λk)，(θ,z,λk)，(θ,z,λk)与z无关，于是式(1)可简化写成

图1 三维V形切口结构Fig.1 A 3-D V-notched structure

图2 三维V形切口结构挖去小扇形柱体Fig.2 A sectoral column is separated from the 3-D V-notched structure

考虑各向同性均质材料，将式(2)代入三维弹性力学几何方程和本构方程，可用位移场函数表示应力场函数(为简明起见，以下分别简写为

式中，(···)′=d(···)/dθ，余下同.G=E/[2(1+v)]，E为材料杨氏模量，v是泊松比.

注意到式(1)的位移特征指数λk和位移特征角函数仅取决于切口的材料性质和楔形边界条件，不依赖载荷，因此应力特征分析不用考虑体力.取式(2)中的典型项Akrλk+1(θ,λk)，Akrλk+1(θ,λk)，Akrλk+1(θ,λk)代入到忽略体力项的三维弹性力学平衡方程

通过一系列推导，可得关于切口尖端扇形柱区域应力奇异性特征值问题的常微分方程组(为方便起见，分别简写为)

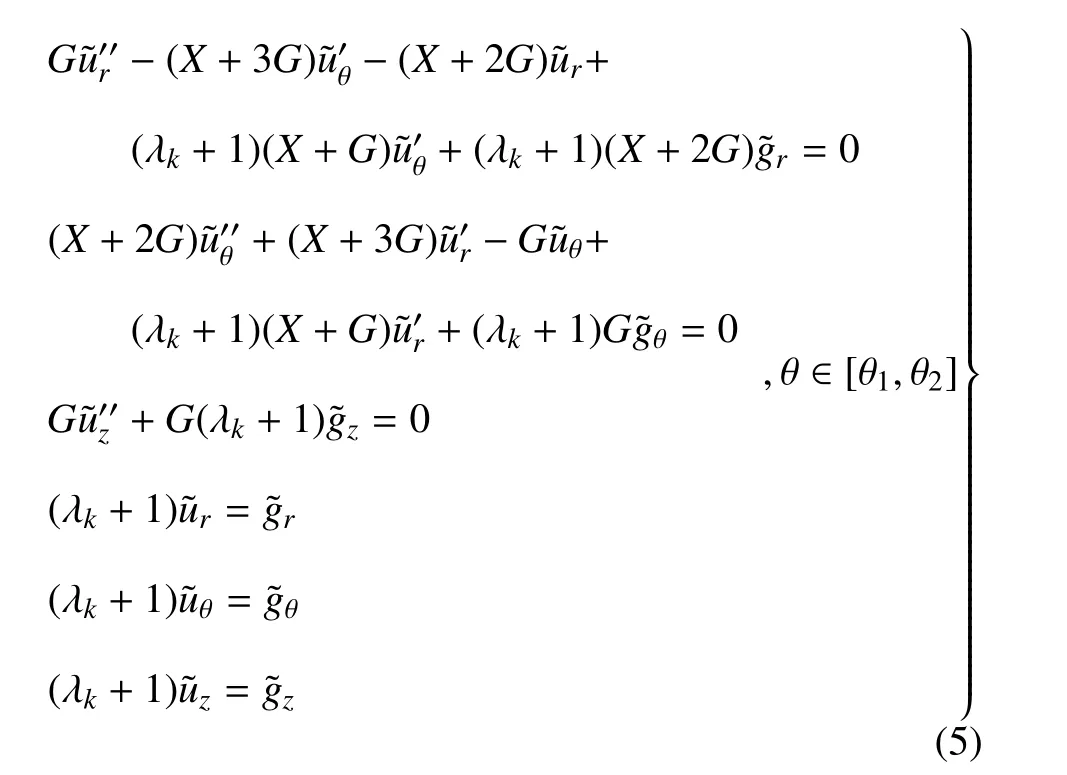
式中，(···)′′表示对坐标θ 的二阶导数，余类同.X=Eν/[(1+ν)(1-2ν)]=2Gν/(1-2ν).

假定切口两楔边自由，则其上面力为零，边界条件可由式(6)表示

因此，三维V 形切口尖端扇形柱附近的位移特征指数λk的计算变成了求解常微分方程组(5)和相应的边界条件(6)的特征值问题.采用插值矩阵法[27-28]求解式(5)和式(6)，可得切口尖端扇形柱附近的位移特征指数λk、相应的位移特征角函数及其导函数.

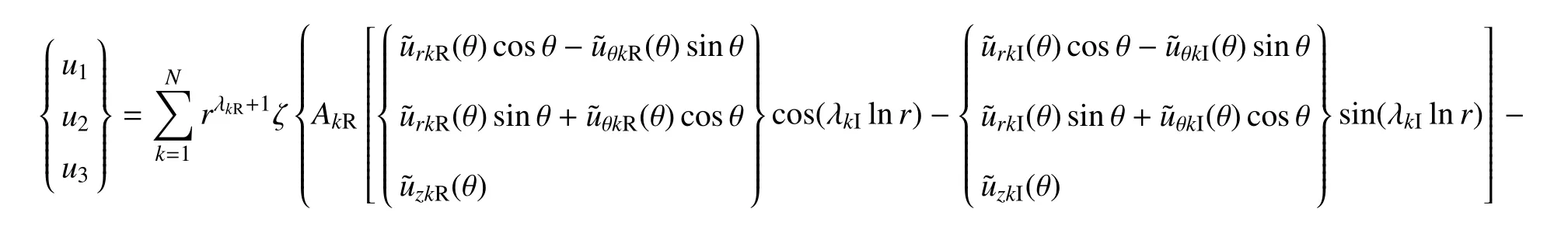
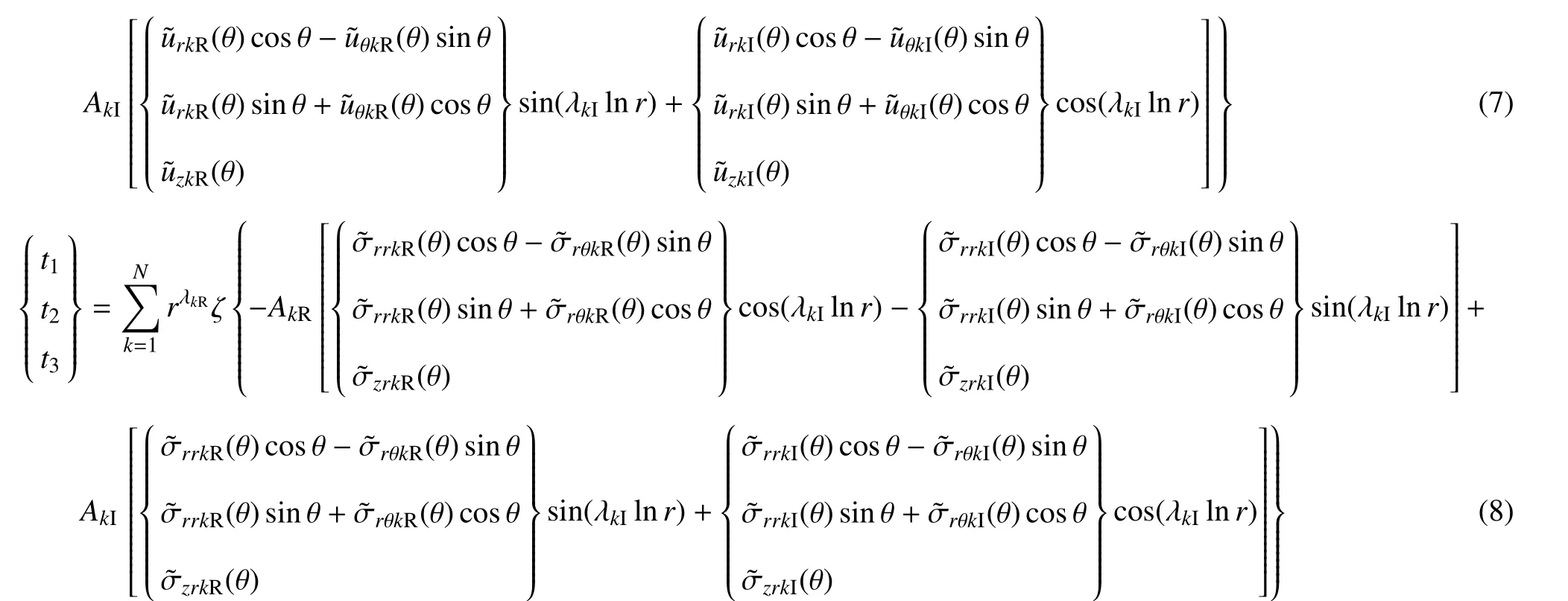
式中，下标R 表示复数的实部，下标I 表示复数的虚部.若λk是实根，则其相应虚部项为零，系数ζ=1；如果λk是共轭复根，则相应虚部项不为零，系数ζ=2，因需计及复数共轭项对位移场和应力场的贡献.

注意：式(7)和式(8)中位移幅值系数AkR和AkI(k=1,2,···,N)待求.基于切口尖端应力奇异性的特征分析结果式(7)和式(8)，下面建立求解三维切口结构位移和应力渐近场表达式中幅值系数AkR和AkI的扩展边界元法.

2 分析三维V形切口/裂纹结构完整应力场的扩展边界元法

在图1 切口结构中挖去尖端扇形柱后剩余的外围结构区域Ω′无应力奇异性，见图2(a).其边界位移um(x)和面力分量tm(x)可由如下常规边界积分方程描述

外围结构Ω′内任意点的位移和应力可分别由位移和应力边界积分方程表达

3 三维V 形切口/裂纹问题算例

3.1 含V 形切口的长方形柱体

含V 形切口的长方形柱体，见图3.结构尺寸L=15 mm，H=5 mm，B=10 mm，弹性模量E=200 GPa，泊松比ν=0.3.沿长方形柱体正表面对称线上有一个等深度的V 形切口，切口深度a=2.5 mm，切口张角2α=60°.长方形柱体结构左侧面(x2=L)固定，右侧面(x2=-L)施加均匀的外部拉力qx=0 MPa，qy=30 MPa.

首先从三维V形切口结构(如图3 所示)中挖取一个ρ=0.5 mm 的扇形柱体(如图4(b)所示)，采用插值矩阵法对扇形柱体进行特征分析，获得三维V形切口尖端扇形柱区域的前若干阶位移特征指数λk和其相对应的位移特征角函数,,，如表1 和图5 和图6 所示.

图3 三维V形切口结构Fig.3 A 3-D V-notched structure

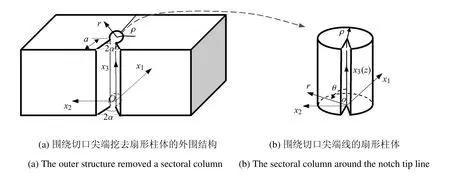
图4 三维V形切口挖去小扇形柱体Fig.4 A sectoral column is separated from the 3-D V-notched structure

表1 三维V 型切口2α=60° 尖端的位移特征指数λkTable 1 The displacement indexes λk of the 3-D V-notched structure with 2α=60°

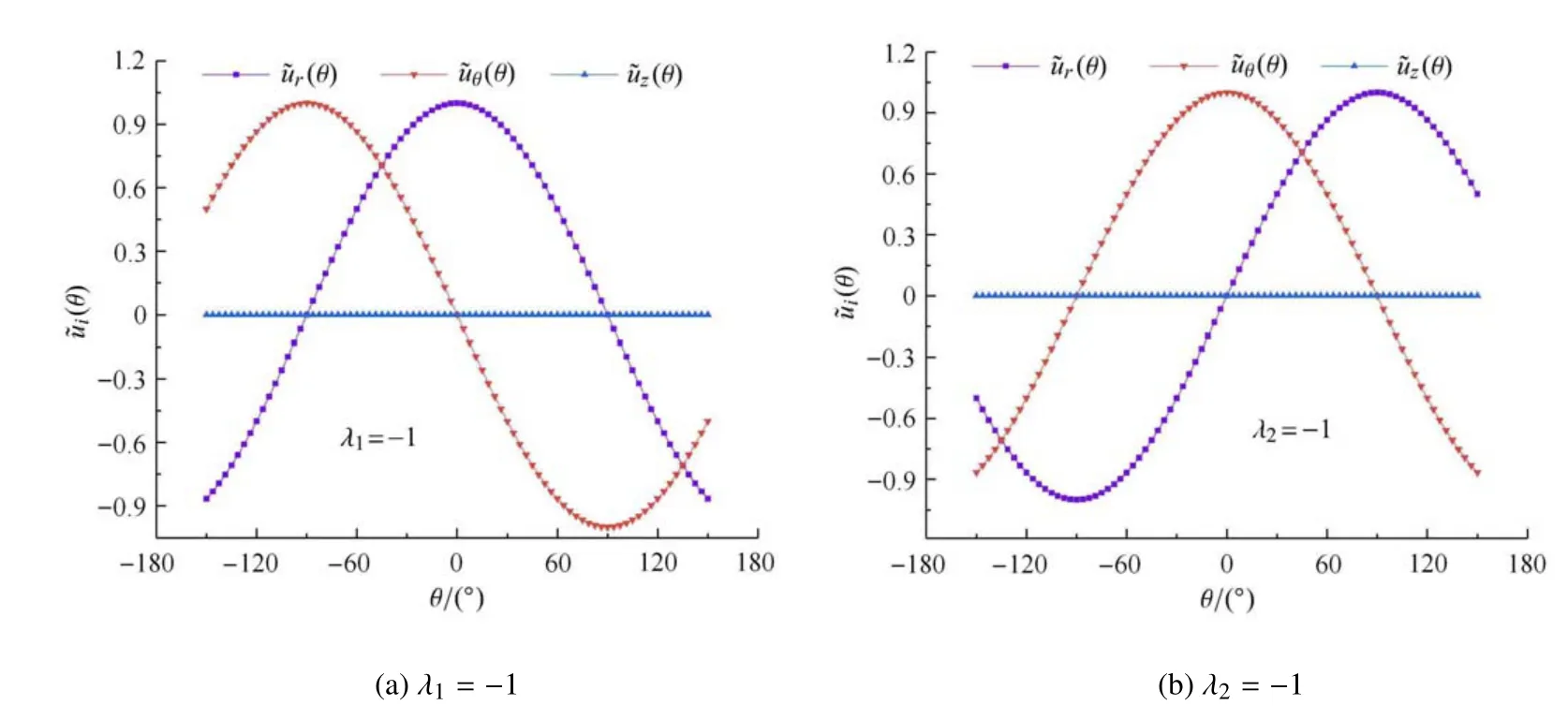
图5 三维V 形切口2α=60° 对应的位移特征角函数Fig.5 The displacement eigenvectors for the 3-D V-notched structure when 2α=60°

图5 三维V 形切口2α=60° 对应的位移特征角函数(续)Fig.5 The displacement eigenvectors for the 3-D V-notched structure when 2α=60° (continued)

图6 三维V 形切口2α=60° 对应的位移特征角函数Fig.6 The displacement eigenvectors for the 3-D V-notched structure when 2α=60°

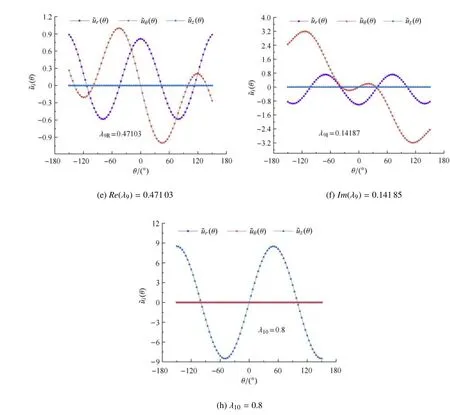
图6 三维V 形切口2α=60° 对应的位移特征角函数(续)Fig.6 The displacement eigenvectors for the 3-D V-notched structure when 2α=60° (continued)

表1 中λk前4 项是刚体位移项，相应的特征角函数见图5.图5(a)～图5(c)呈现的是平面问题的3 个刚体位移项，图5(d)呈现的是反平面问题的刚体位移项.这些刚体位移项对应力场的计算没有影响，但对于位移场的计算不可省略.

注意到图6(b)、图6(d)、图6(h)中˜ur和˜uθ均为0，故λ6,λ8和λ10为反平面V 形切口对应的位移特征指数.图6(a)、图6(c)、图6(e)、图6(f)中˜uz均为0，故λ5,λ7和λ9为平面V 形切口对应的位移特征指数；其中，λ5和λ9为平面内对称位移特征指数，λ7为平面内反对称位移特征指数.

扩展边界元法(XBEM)对三维V 形切口结构进行计算时，初始选取渐近级数展开式(1)中截取级数项数N=7(4 个刚体位移项，1 个平面内对称项，1 个平面内反对称项和1 个反平面项)作为渐近级数展开式(1)的基准项数.随后在N=7 的基础上增大N，讨论N的取值对三维V 形切口结构完整位移和应力场精度的影响.

XBEM 分析三维V 形切口结构的实施过程：首先，采用插值矩阵法求解常微分方程组(5)获得切口尖端的位移特征指数λk及其相对应的特征角函数，然后对外围结构采用边界元法进行分析，边界采用8 节点四边形单元，单元数424，节点数1274.联立求解两组方程组获得了位移幅值系数AkR,AkI以及外围结构边界未知的位移和面力.在XBEM 执行中，不可避免遇到有些源点到边界单元距离很小的情形—三维BEM 中几乎奇异积分的难题，本文采用半解析法[4,30]高效解决了这一难题.最后，将求得的边界位移和面力代入式(10)和式(11)得外围结构任意内点的位移和应力.对于扇形柱体区域的位移和应力场，采用渐近级数展开式(1)和式(3)计算，外围区域(图4(a))内点的位移和应力场采用内点积分方程(10)和式(11)计算，其临近扇形柱附近的外围区域内点的位移和应力场也可采用渐近级数展开式(1)和式(3)计算.

表2 和表3 以及图7 分别给出了切口尖端扇形柱一定范围内应力和位移的XBEM 计算结果，其中，XBEM-ASY 表示采用渐近级数展开式(1)和式(3)计算的结果(扇形柱及其临近区域)，XBEMBEM 表示采用积分方程式(10)和式(11)计算的结果(外围区域)，FEM 表示采用有限元分析软件计算的结果.表2 和表3 中XBEM-BEM 计算值和图7(a)曲线显示：当截取级数项数N＞7 时，N的增加对于外围结构区域的XBEM-BEM 计算结果影响很小.说明选取了足够的N之后，XBEM 的计算精度对N的取值不敏感，稳定性很好，这对于XBEM 求解三维V 形切口结构的完整应力场非常便利.

表2 显示，对外围区域点(1.438 mm,0 mm,5 mm)处，当N=7 时，XBEM-ASY 计算的应力值(σx2=32.56 MPa)和XBEM-BEM 计算相同点的应力值(σx2=40.04 MPa)的相对差为-18.7%.当N=8时，XBEM-ASY 计算的应力值(σx2=34.89 MPa)和XBEM-BEM 计算相同点的应力值(σx2=40.04 MPa)的相对差为-12.9%.当N=9 时，XBEM-ASY 计算的应力值(σx2=36.57 MPa)和XBEM-BEM 计算相同点的应力值(σx2=40.04 MPa)的相对差为-8.7%.说明相对XBEM-BEM计算值而言，XBEM-ASY 计算同一点的相对差随N的增大逐渐减小，即XBEMASY 计算切口尖端应力场的有效范围随N的增大逐渐增大.

通常情况，外围结构的位移和应力由XBEMBEM 解胜任，无需采用XBEM-ASY 计算，这里关于两者计算值的比较，意在说明XBEM-ASY 解的有效范围可为扇形柱半径的选取提供参考.例如，若XBEM-ASY 计算的切口尖端应力场在r＜1.0 mm 的范围内是足够准确的，说明XBEM 使用时，尖端扇形区域半径ρ 的选取范围较为宽松，ρ ＜1.0 mm 之间均可行.表3 中切口结构位移解显示了同样的规律.

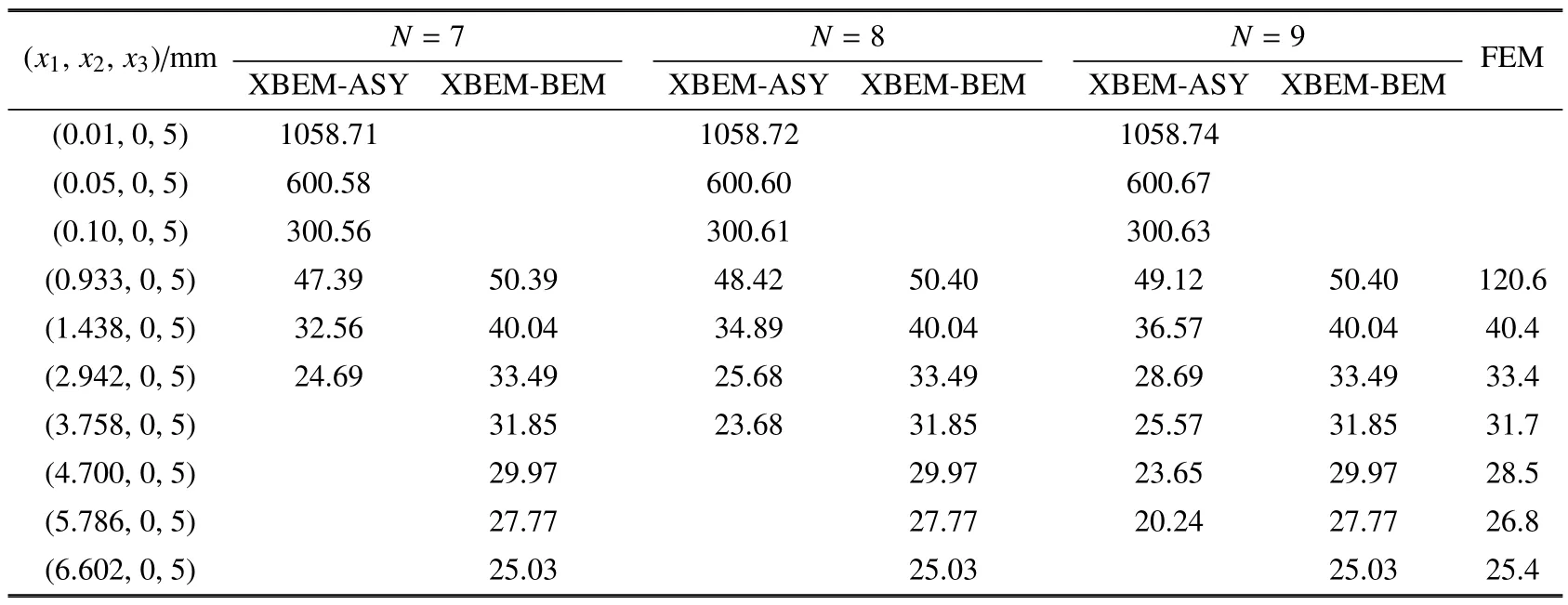
表2 XBEM和FEM 计算沿x2=0 mm, x3=5 mm 附近内点的应力分量σx2(MPa)Table 2 Variation of stress component σx2(MPa)along x2=0 mm, x3=5 mm

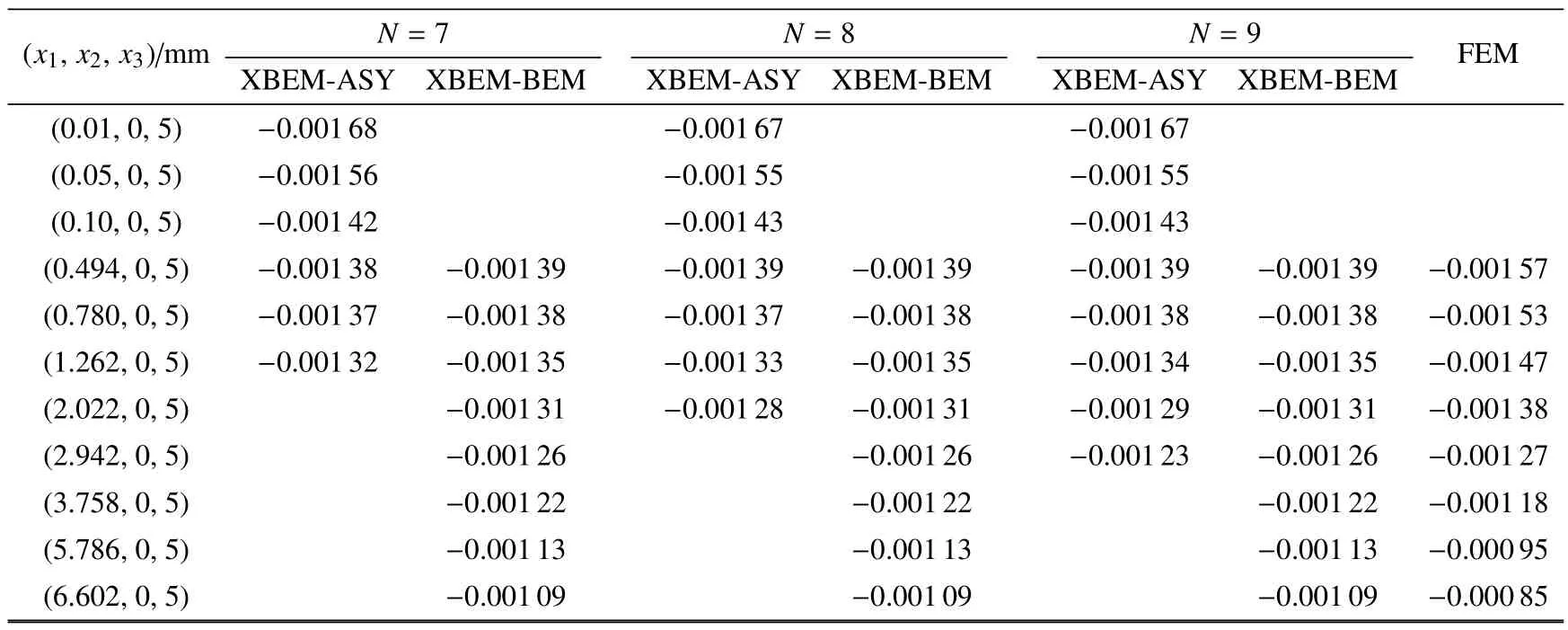
表3 XBEM和FEM 计算沿x2=0 mm, x3=5 mm 附近内点的位移分量ux2(mm)Table 3 Variation of displacement component ux2(mm)along x2=0 mm, x3=5 mm

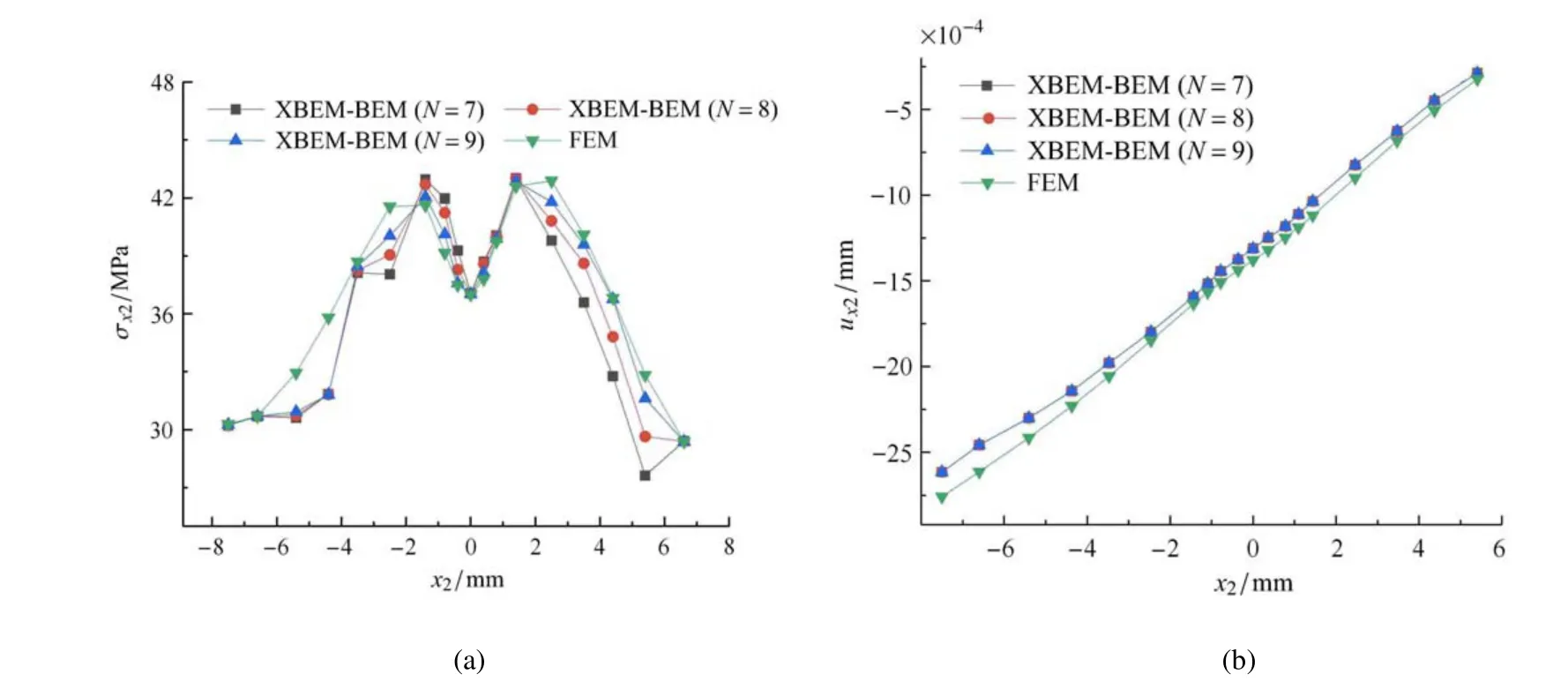
图7 XBEM-BEM 和FEM 计算3-D V 形切口沿x1=2 mm, x3=5 mm 线段的σx2 和ux2 值Fig.7 σx2 and ux2 along x1=2 mm, x3=5 mm calculated by XBEM-BEM and FEM

此外，本文还采用有限元法(FEM)对图3 结构进行计算.这里FEM 采用20 节点六边形单元，划分单元数111 000.表2 显示，当x2=0 mm，x3=5 mm，x1＞ 1.262 mm 的远场区域，FEM 的结果和XBEM-BEM 的结果吻合较好；而当x2=0 mm，x3=5 mm，x1＜ 1.262 mm 时(切口尖端近场区域)，FEM 计算的应力场与XBEM-BEM 的结果有较大的差异.对于三维V 形切口尖端的强应力集中，尽管FEM 在尖端使用了细密的网格划分，其采用的单元数为XBEM 单元数的261 倍，极大地增加了计算量和计算机内存需求，但仍无法准确描述其尖端近场区域的应力场.随着距尖端距离的增大，应力集中的现象逐渐减弱，FEM 的计算结果方为可信.

3.2 含裂纹的长方形柱体单向受拉和受剪

含裂纹的各向同性均质材料长方形柱体，结构尺寸L=10.0 mm，H=3 mm，B=4 mm，弹性模量E=200 GPa，泊松比ν=0.3.沿长方形柱体正表面对称线上有一个等深度的裂纹，裂纹深度a=0.8 mm，边界条件为长方形柱体结构左侧面固定，右侧面施加均布载荷qx=10 MPa，qy=10 MPa，为复合型裂纹，如图8 所示.

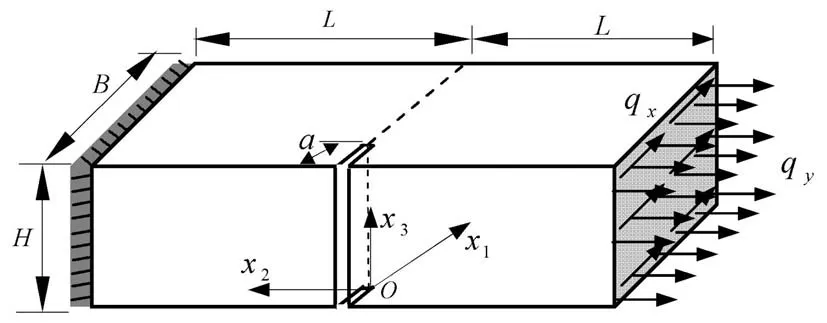
图8 三维裂纹结构Fig.8 A 3-D cracked structure

图9 三维裂纹挖去小扇形柱体Fig.9 Asectoral column is separated from the 3-D cracked structure

首先从图8 三维复合型裂纹结构中挖取一个ρ=0.2 mm 的扇形柱体(如图9(b)所示)，采用插值矩阵法对扇形柱体进行特征分析，获得裂纹尖端扇形柱区域的前若干阶位移特征指数λ1,λ2,λ3,···,λ10分别为-1,-1,-1,0,-0.5,-0.5,-0.5,0,0.000 01,0.5.其相对应的位移特征角函数˜ur,˜uθ,˜uz如图10 所示.

图10 三维裂纹对应的位移特征角函数Fig.10 The displacement eigenvectors for the 3-D cracked structure

λ1～ λ4前4 项是刚体位移项，λ5～ λ10为主导的各阶位移特征指数，其对应的位移特征角函数见图10.注意到图10(b)、图10(d)、图10(h)为反平面裂纹对应的位移特征角函数；图10(a)、图10(c)、图10(e)、图10(f)为平面裂纹对应的位移特征角函数.

图11 三维裂纹结构边界元网格Fig.11 The BE meshes of 3-D cracked structure

表4 和表5 以及图12 结果显示：选取不同的截取级数项数N，XBEM-BEM 计算相同点的应力和位移值基本相等，说明XBEM 计算三维复合型裂纹结构应力场和位移场的数值稳定，XBEM 的计算精度对截取级数项数N的选取不敏感，便于XBEM 的应用.

表4 还显示，在外围区域点(1.70 mm,0 mm,3 mm)处，当N=7 时，XBEM-ASY 计算的应力值(σx1=4.665 MPa)和XBEM-BEM 计算相同点的应力值(σx1=6.407 MPa)的相对差为-27.2%.当N=8时，XBEM-ASY 计算的应力值(σx1=5.314 MPa)和XBEM-BEM 计算相同点的应力值(σx1=6.417 MPa)的相对差为-17.2%.当N=9 时，XBEM-ASY 计算的应力值(σx1=5.544 MPa)和XBEM-BEM 计算相同点的应力值(σx1=6.527 MPa) 的相对差为-15.1%.说明相对XBEM-BEM 计算值而言，XBEMASY 计算同一点应力的相对误差随N的增大逐渐减小，即XBEM-ASY 计算裂纹尖端应力场的有效范围随N的增大逐渐增大.同理分析表5 可得，XBEM-ASY 计算裂纹尖端位移场的有效范围随N的增大逐渐增大.

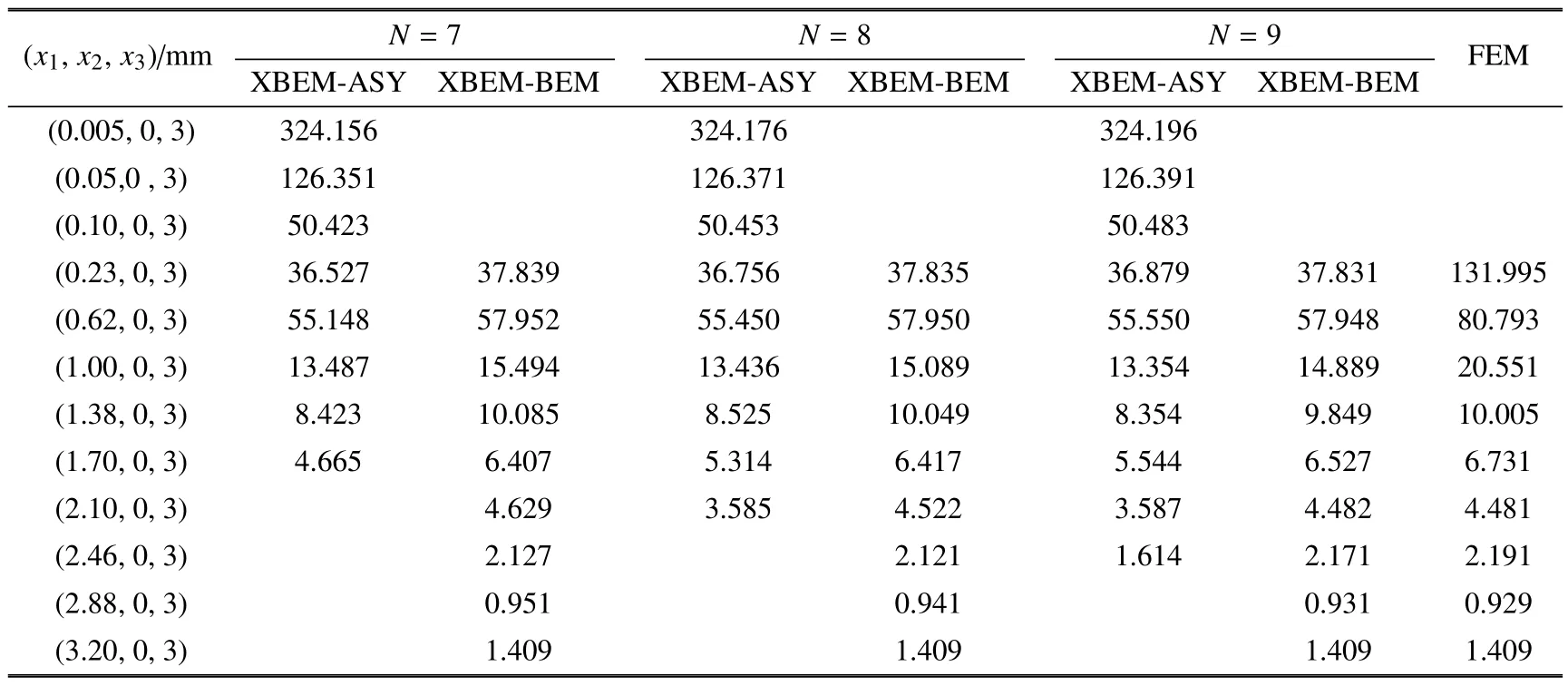
表4 XBEM和FEM 计算沿x2=0 mm, x3=3 mm 附近内点的应力分量σx1(MPa)Table 4 Variation of σx1(MPa)along x2=0 mm, x3=3 mm calculated by XBEM and FEM

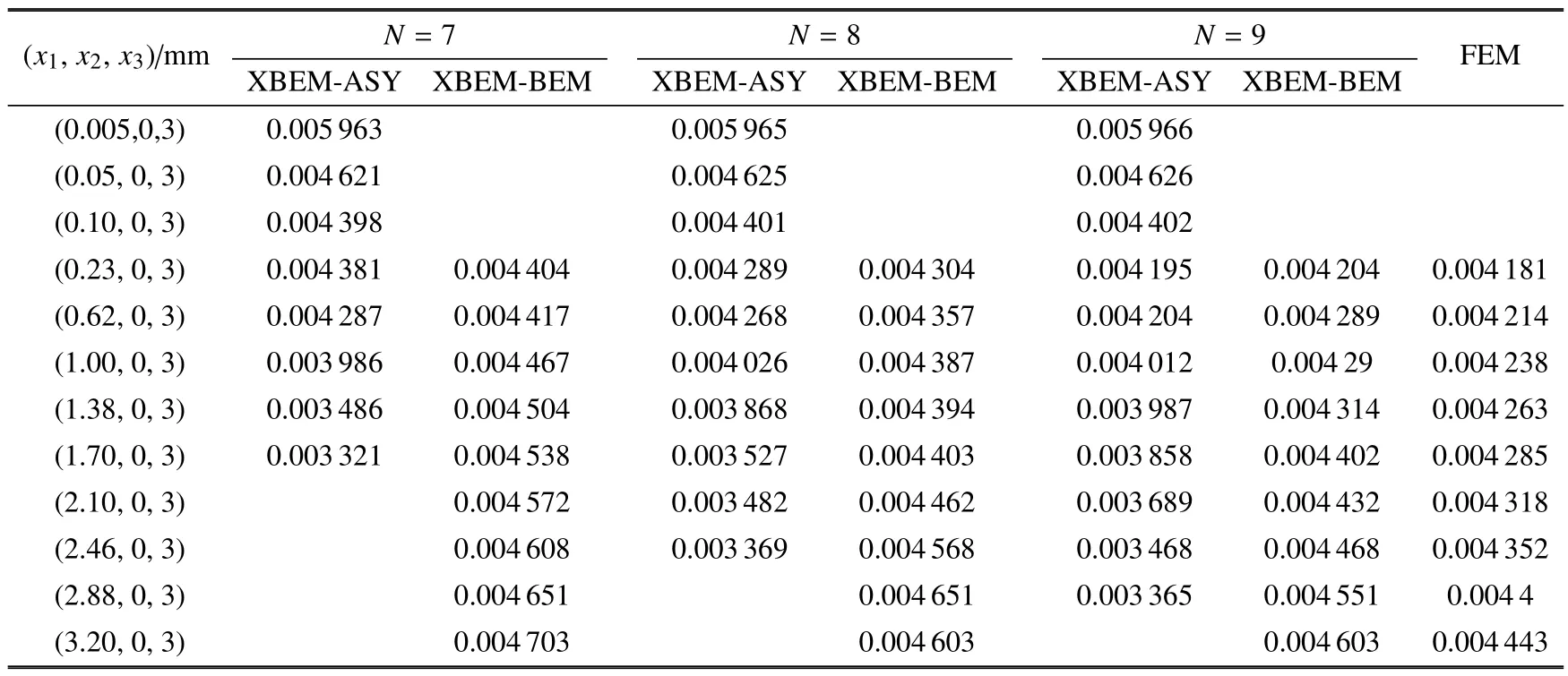
表5 XBEM和FEM 计算沿x2=0 mm, x3=3 mm 附近内点的位移分量ux1(mm)Table 5 Variation of ux1(mm)along x2=0 mm, x3=3 mm calculated by XBEM and FEM

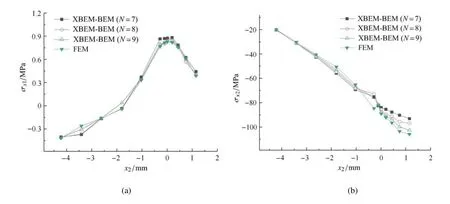
图12 XBEM-BEM 和FEM计算沿x1=2.88 mm, x3=3 mm 附近内点的应力分量Fig.12 The stress component along x1=2.88 mm, x3=3 mm calculated by XBEM-BEM and FEM

通常情况，外围结构的位移和应力由XBEMBEM 解胜任，无需用XBEM-ASY 计算.这里关于两者计算值比较，意在说明XBEM-ASY 解的有效范围内，均可作为扇形柱半径的选择范围.例如，若XBEM-ASY 计算的裂纹尖端应力场在r＜0.2 mm 的范围内是足够准确的，说明XBEM使用时，尖端扇形区域半径ρ 的选取范围较为宽松，ρ ＜0.2 mm 之间均可行.

表5 显示，当x2=0 mm，x3=3 mm，x1＞1.38 mm 的远场区域，FEM 的结果和XBEM-BEM 的应力结果吻合较好，而当x2=0 mm，x3=5 mm，x1≤1.38 mm 时，FEM计算的应力场(裂纹尖端近场区域)与XBEM-BEM 的结果有较大的差异.对于三维裂纹尖端的强应力集中，尽管FEM 在尖端使用了细密单元，结构采用20 节点六边形单元，划分单元数141 000，XBEM 使用单元数808，FEM 采用的单元数为XBEM 的163 倍，这极大地增加了计算量和计算机内存需求，但仍无法准确描述其尖端近场区域的应力场.随着距尖端距离的增大，应力集中的现象逐渐减弱，FEM的计算结果变得可信.而本文方法可采用较少的单元数来准确获取三维裂纹结构完整的应力场，进一步表明了XBEM 处理V 形切口应力集中问题的优越性.

4 结论

本文建立了三维线弹性V 形切口/裂纹结构完整应力场分析的扩展边界元法，并对三维V 形切口/裂纹结构在典型载荷工况下进行了计算，结论如下.

(1) 将三维柱状V 形切口/裂纹结构分离为尖端扇形柱区域和外围结构区域，扩展边界元法发挥了切口尖端扇形柱区域渐近分析和外围结构边界元法分析特长.XBEM 类似于半解析方法，在切口尖端扇形柱区域位移和应力由渐近级数展开式表达，远端区域的力学场由边界元法分析.文中算例结果显示了XBEM 可准确获取三维V 形切口/裂纹结构完整的位移和应力场，有利用于判定三维裂纹结构的起裂扩展.

(2)尖端扇形柱区域的渐近级数展开式选取的截取级数项数N越大，则渐近级数展开式计算尖端应力和位移场的有效范围越大，说明尖端扇形柱半径的选取范围越大.

(3) 按照线弹性理论分析，三维V 形切口/裂纹尖端附近的应力值随r→0 趋近无限大，尖端区域发生了塑性变形.后续将研究考虑三维V 形切口/裂纹结构尖端附近塑性变形的扩展边界元法分析.