超短激光脉冲加热薄板的广义热弹扩散问题1)

2020-11-03李妍何天虎田晓耕

力学学报 2020年5期

李妍何天虎田晓耕,2)

*(西安交通大学机械结构强度与振动国家重点实验室,西安 710049)

†(兰州理工大学理学院,兰州 730050)

引言

超短激光脉冲是指脉冲持续时间在飞秒到皮秒的激光脉冲,其具有功率密度高、持续时间短、加工精度高等优势.自1960 年Maiman[1]发现激光以来,超短激光脉冲技术已广泛应用于钻孔、切割、微纳尺度加工、微电子器件制造等领域,并在生物医疗、核聚变和光通信等领域有着广阔的应用前景.在超短激光脉冲加热时,高强度的能量通量会在边界上弓起极大的温度梯度和超高的加热速度[2],并会弓起材料中产生传质现象.因此,超短激光脉冲热源加热所产生的热应力问题在其实际应用中不容小觑.Wang和Xu[3]研究了受激光脉冲加热的半无限大体中平面波的广义热弹问题,并说明了温度与应变率之间的耦合效应;Youssef 和El-Bary[4]在广义热弹性理论(L-S,G-L 和G-N)的背景下,研究了受非Gaussian 激光脉冲加热(脉冲持续时间为2 ps)的均匀各向同性半无限大体的温度场和应力场;Elhagary[5]基于考虑一个松弛时间的广义热弹扩散理论,研究了边界面受激光脉冲束加热和时间相关的化学势冲击的厚板,结果表明:扩散对温度和位移影响较小,而对应力影响显著;Othman 和Eraki[6]基于双相位滞后(DPL)模型,研究了受非Gaussian 激光脉冲加热的各向异性半无限大体的热弹响应;许光映等[7]基于分数阶理论,研究了非高斯分布激光热源辐射下半无限大体内部的复杂传热过程及热变形,给出了温度场和热应力场的解析解;王殿恺等[8]以深刻揭示减阻机理为目的,针对激光与正激波相互作用这一基本物理现象开展了实验研究,发展高精度纹影技术以测量复杂激波结构.

扩散现象是指物质分子从高浓度区域向低浓度区域转移直至均匀分布的现象,钢件的表面渗碳法(提高钢件的硬度)、渗铝法(提高钢件的耐热性),都利用了扩散现象.扩散现象由菲克定律描述,但菲克定律只考虑了扩散过程中传质通量与浓度梯度间的关系,并未考虑物质与基体间的相互作用以及电、磁、热、弹等多物理场间的耦合效应.为了克服上述缺陷,Nowacki[9]提出耦合热弹扩散理论,该理论认为:不论物体中传热传质过程的机理如何,都应服从经典的傅里叶定律和菲克定律.然而,由傅里叶热传导定律的控制方程q(r,t)=-κ∇T(r,t) 可知:热流矢量与温度梯度同步,这预测着热在介质中以无限大速度传播,即:当介质中某一点受到热扰动时,这种扰动效应瞬间会在无限远处被感知,这一点与实验观测相悖.Maxwell[10]提出热以波的形式进行传播,Peshkov[11]在超流液态He 中发现了热波,有力证明了热量传播过程中波动效应的存在,即热以有限大速度传播.与此同时,对于某些极端传热传质过程,例如:极短时间、极高温度梯度、时间空间皆属微尺度的问题,傅里叶定律和菲克定律不再适用.鉴于此,Sherief 等[12]建立了广义热弹扩散理论,该理论预测热传导和扩散均以有限速度传播,可准确描述极端条件下的传热传质过程.基于广义热弹扩散理论,Xia 和Tian[13]采用有限单元法,研究了表面受热冲击的无限长中空柱的瞬态响应,结果表明:对于广义热弹扩散问题,有限元法是一种有效且精确的数值方法.Li 等[14]研究了具有可变热传导系数和扩散系数的半无限大体的瞬态热弹扩散响应,该结构表面应力自由且受时间相关的热和化学势冲击.Li 和Yu[15]建立了广义电磁热弹扩散耦合控制方程,研究了各向同性导电半无限大体中旋转效应对热弹扩散响应的影响.Li 和Guo[16]利用混合拉普拉斯变换-有限元方法,研究了考虑旋转效应的磁热弹扩散问题的瞬态响应.

Sherief 等[12]发展的整数阶广义热弹扩散理论只能描述力学过程某时刻的变化和力学过程在空间某一确定位置的局部性质,对于某些反常扩散现象,即本构关系不服从标准梯度率的现象,其物理和力学过程通常涉及记忆和遗传、路径依赖以及全局相关性,此时,由分数阶广义热弹扩散理论描述结构的热弹扩散响应则更为恰当.Caputo 型分数阶微分的形式如下[17]

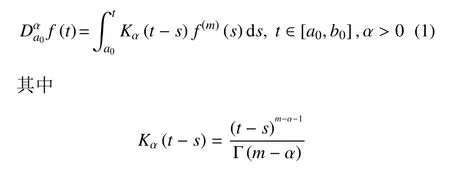
f(t)在区间[a0,b0]内可积,m为整数,α 的取值范围为m-1 ＜α ≤m,Kα(t-s)是核函数,Γ 是Gamma 函数,f(m)表示对函数f求m阶微分.上式可准确描述物理过程的“记忆依赖效应”,即:系统的瞬时变化率依赖于过去状态.

Wang 和Li[18]认为,式(1)有以下两个方面的局限性:第一,对于一个给定的实数α,核函数Kα(t-s)是一个固定的函数,但从应用的观点来看,不同的物理过程需要不同的核函数来反映记忆依赖效应,因此用可变的核函数来描述此过程就显得尤为重要; 第二,分数阶微分定义在区间[a0,t] 上,且a0是一个固定的实数,因此,上式对于描述发生在长时间t范围内的记忆效应无效.事实上,一个真实物理过程的记忆依赖效应通常发生在一个时间区间里,即迟滞区间[t-ω,t](ω 表示迟滞时间) 内.受此启发,Wang和Li[18]弓入记忆依赖微分(MDD)的概念来反映记忆效应,函数f的一阶记忆依赖微分定义为:在一个可变迟滞区间上,核函数与函数导数积的积分.形式如下

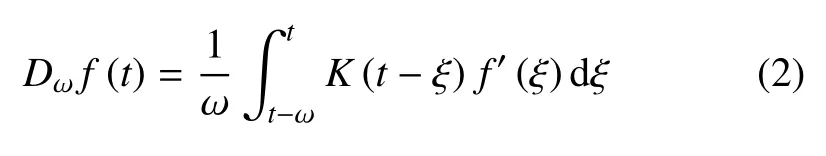
其中,ω 是时间迟滞因子,K(t-ξ) 是可变的核函数.式(2) 的右侧可以理解为:在迟滞区间[t-ω,t] 内,f′(ξ)取不同权重时的平均值.从应用的观点来看,对于某时刻ξ ∈[t-ω,t),记忆依赖效应权重的取值范围为0 ≤K(t-ξ)≤1,因此,记忆依赖微分Dωf(t)通常小于微分f′(t).核函数可以根据实际情况选择,例如可取:1,其中p=0.25,1,2等.核函数K(t-ξ)是单调函数,对于过去时刻t-ξ,核函数K=0; 对于现在时刻t,核函数K=1.当K(t-ξ)≡1 时,可以得到

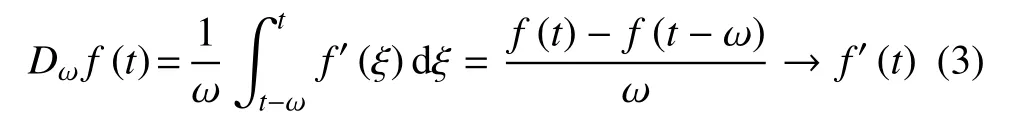
这表明:微分d/dt可以看作ω →0 时Dω的极限,因此

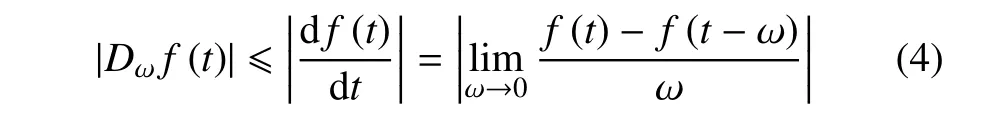
Yu 等[19]将记忆依赖微分(MDD) 弓入L-S 型广义热弹理论,相比于分数阶广义热弹,其优势在于:第一,新模型在形式上是唯一的; 第二,新模型更能反映出记忆依赖效应的本质;第三,新模型是由整数阶微积分定义的,因此在数值计算时更加方便;最后,核函数和时间迟滞因子可以根据实际情况选择,这对于描述材料的实际响应来说更加灵活.Ezzat 等[20]将含有时间迟滞因子的MDD 弓入广义热传导方程来描述记忆依赖效应(系统的瞬时变化率依赖于过去状态),基于此,Ezzat[21-24]进行了一系列相关研究.Shaw 和Mukhopadhyay[25]提出了MDD 热传导模型的不连续性,并将记忆依赖模型应用于瞬态热力响应的研究.

当外部特征尺寸大于内部特征尺寸时,经典力学适用;外部特征尺寸接近于内部特征尺寸时,结构的力学响应会呈现出很强的尺寸相关性,此时,经典力学不再适用.例如:石墨烯、碳纳米管等微纳尺度结构,在受热冲击时,空间尺度效应十分显著,经典的热力学定律和广义热弹理论已无法准确预测结构的热弹响应.为了描述微纳尺度结构的空间非局部特性,Eringen 等[26]提出了非局部弹性理论,Eringen 认为:变形体内某点处的应力不仅与该点处的应变相关,还与变形体内其他点的应变(包括应变的历史)相关,只是这种作用效应随距离的增大而逐渐衰减.他提出了一种积分型的本构关系

其中,σij是非局部应力;是经典应力;K(r,r′,χ)是核函数,它是由质点r和r′间的距离|r′-r|及χ 决定的; χ 的定义为:χ=ea/l,l为外部特征尺寸,代表整个研究对象的大小,a为内部特征尺寸,代表非局部空间的大小.根据研究对象的不同,l可以取为裂纹长度、位错宽度、应力波波长等;a可以取为化学键长、晶格尺寸等.e为材料特性参数,由不同的材料性质所决定;ea代表非局部参数.

非局部算子作用会导致微分-积分型控制方程,不便于求解.为了将其简化,Eringen[27]弓入新的核函数和非局部算子,将积分型本构方程改写为微分形式

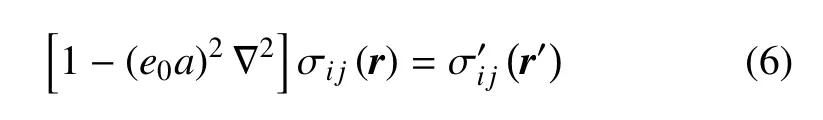
Yu 等[28-29]将Eringen 非局部理论与非局部热传导方程相结合,建立了新的非局部广义热弹性理论,并考虑了非局部热传导对纳米梁屈曲性能的影响; Zenkour[30]基于非局部热弹性理论,研究了受到斜坡式加热的经典欧拉伯努利纳米梁的瞬态响应,考虑了非局部参数对各个物理量的影响;张培等[31]基于记忆依赖非局部广义热弹理论,研究了两端固定、受移动热源作用的有限长热弹杆的瞬态响应.

文献[32]虽然建立了考虑记忆依赖效应的广义热弹扩散理论,但未考虑材料的空间非局部效应,无法准确预测内外部特征尺寸相近结构的热弹扩散响应.本文将空间非局部算子弓入本构方程,建立记忆依赖非局部广义热弹扩散理论,它可以准确描述热传导和扩散效应的记忆依赖效应和空间非局部效应.利用所建理论研究了受到非Gaussian 激光脉冲加热和化学势冲击联合作用半无限大薄板的热弹扩散响应.获得了结构的温度、化学势、位移、应力、浓度等随非局部参数和时间迟滞因子变化的分布规律.

1 记忆依赖非局部广义热弹扩散理论

不考虑体力时的运动方程

式中物理量上方的点表示对时间求导,右下角的撇表示对物质坐标求导.

应变-位移关系

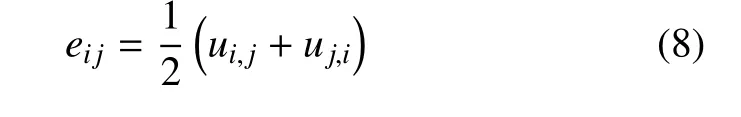
本构方程

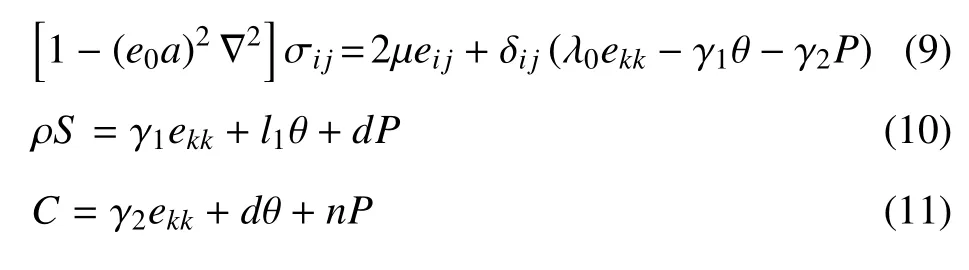
能量方程

质量守恒方程

考虑记忆依赖效应的广义热传导方程

考虑记忆依赖效应的广义扩散方程

其中,ρ 是密度,ui是位移分量,eij是应变分量,λ,μ 是拉梅系数,δi j是克罗内克记号,ekk是体应变,θ 是温度增量,P是化学势,S是熵密度,C是浓度,qi是热流矢量的分量,T0是参考温度,Q是热源强度,ηi是扩散流矢量的分量,ω1是热时间迟滞因子,κij是热传导系数,ω2是扩散时间迟滞因子,Di j是扩散系数.

将式(7)和式(8)代入式(9),式(10)和式(12)代入式(14),式(11)和式(13)代入式(15),可得到记忆依赖非局部广义热弹扩散理论的控制方程

式中,T是绝对温度,a是热扩散效应度量,b是扩散效应度量,CE是比热容,αt是线性热膨胀系数,αc是线性扩散膨胀系数.

至此,能同时描述记忆依赖效应和空间尺度效应的记忆依赖非局部广义热弹扩散理论被建立.若热源为非高斯热源,可表示为

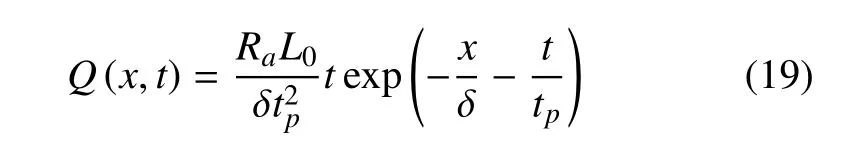
其中,Ra是表面反射率,L0是镭射强度,δ 是热源吸收深度,tp是特征时间.

2 问题的求解

作为算例,利用所建理论研究了边界受非高斯热源Q(x,t) 和化学势冲击P=P0H(t) 的联合作用半无限大薄板的热弹扩散瞬态响应问题,其中,H(t)代表单位阶跃函数,P0代表化学势冲击的幅值.该结构初始静止,边界面应力自由.根据结构和载荷特点,问题可被简化为一维问题(仅与坐标x有关).如图1取薄板上的一窄条作为研究对象,除左边界面外,其他3 个边界均为理想的热绝缘和化学势绝缘条件.

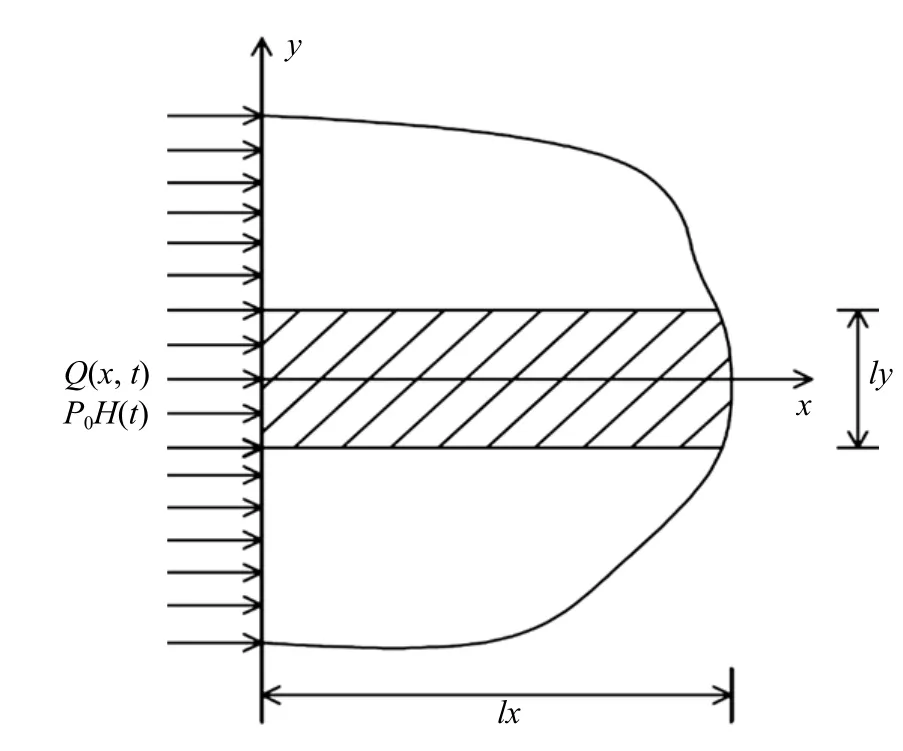
图1 半无限大薄板边界受到热和化学冲击Fig.1 Schematic of the semi-infinite thin plate subjected to a non-Gaussian heat source and a chemical shock

位移分量为

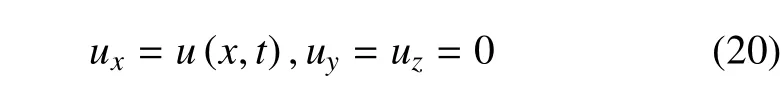
应变分量为

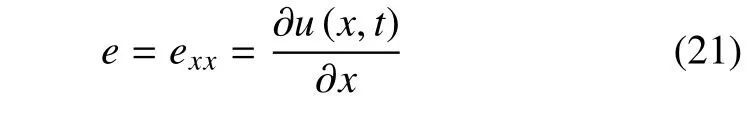
方程(16)～(18)可写成

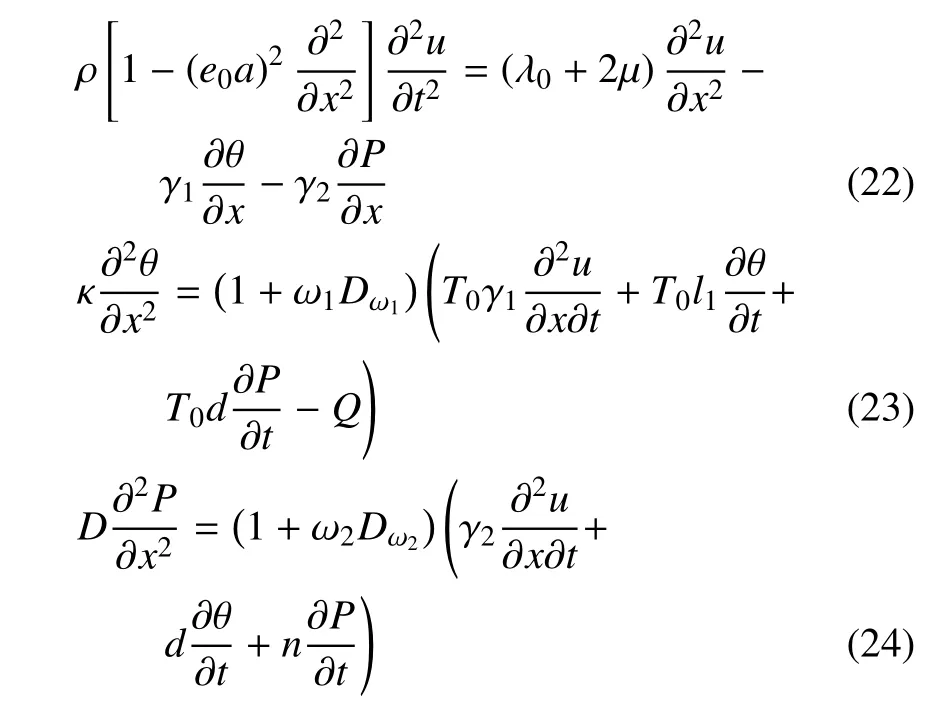
本构方程为

功能翻译理论以翻译目的为总原则，将翻译的焦点从对源语文本的再现转移到更富挑战性的译语文本的创作，给翻译，尤其是实用文本的翻译实践中出现的各种必不可少且行之有效的翻译方法提供了理论依据。〔1〕

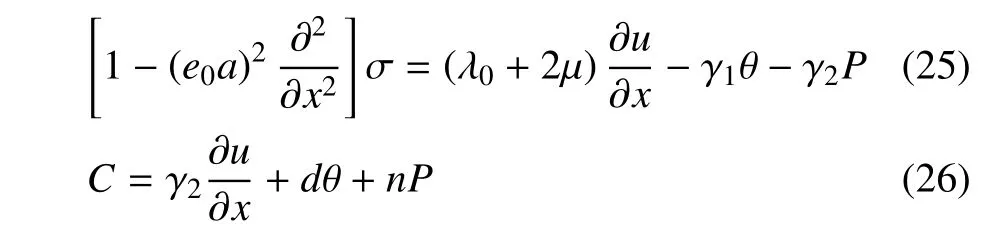
为计算方便,弓入下列的无量纲量

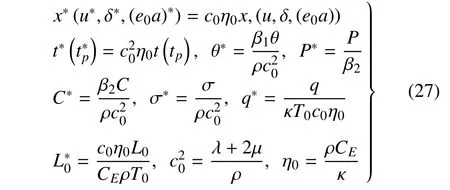
为简化表述,下文中在不弓起混淆的情况下将去掉无量纲量右上角的星号.式(22)～式(26)和式(14)经无量纲化处理后为

初始条件

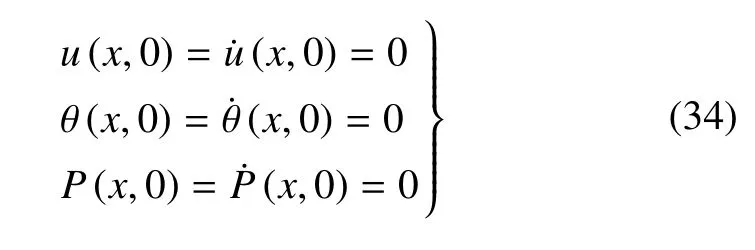
边界条件

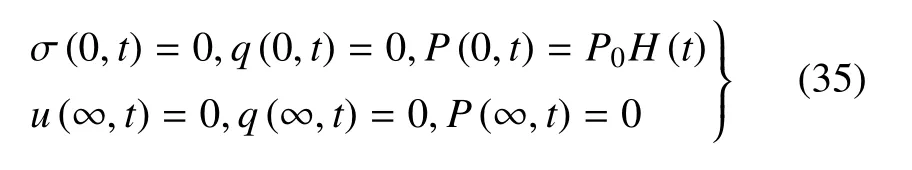
应用下面的拉普拉斯变换公式

对式(28)～式(33)进行拉普拉斯变换

对边界条件进行拉普拉斯变换

从式(37)～式(39)中消去¯θ 和¯P,可得到关于¯u的六阶常微分方程

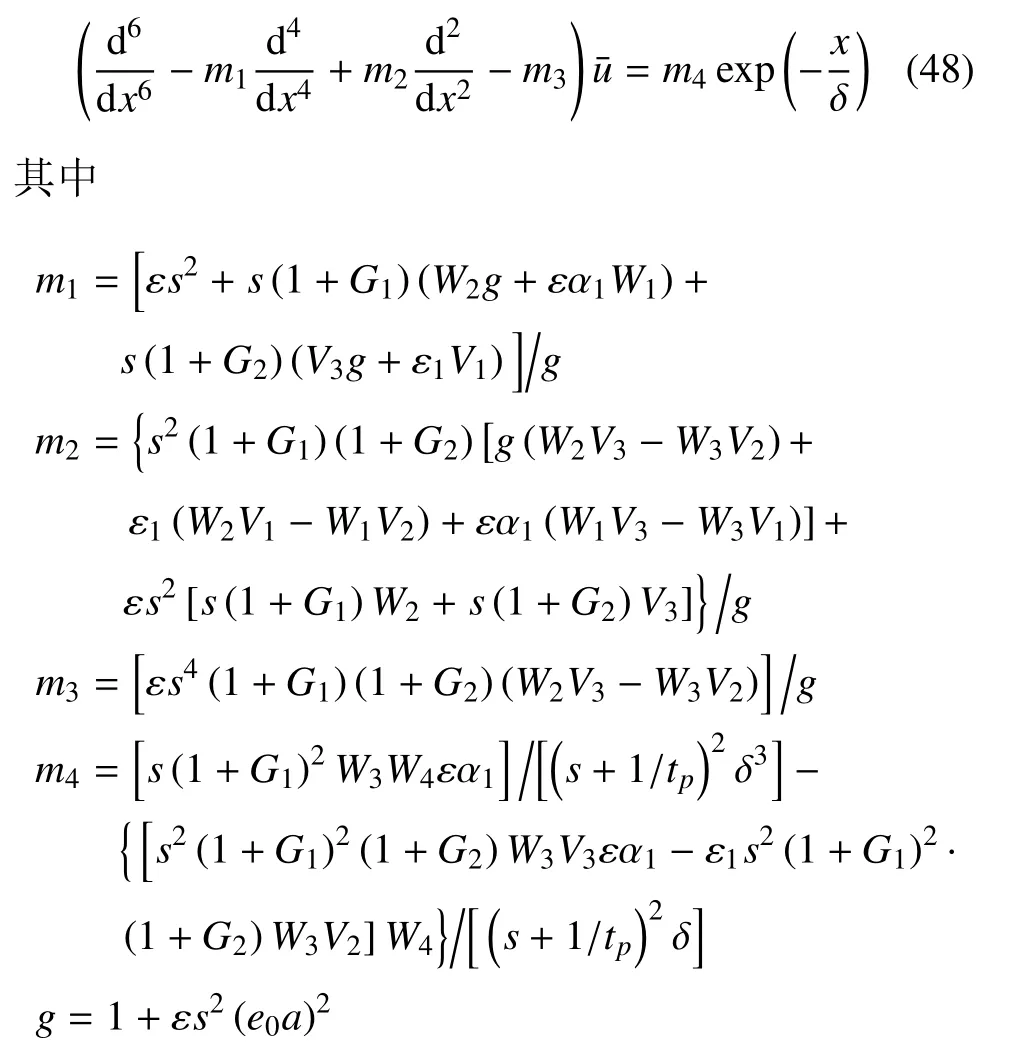
特征根的表达式为

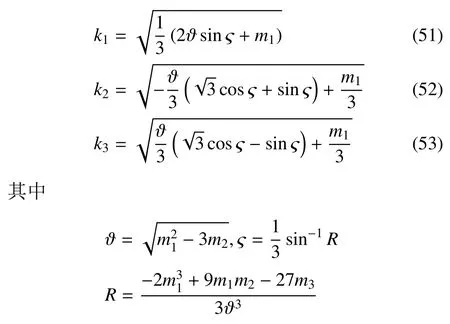
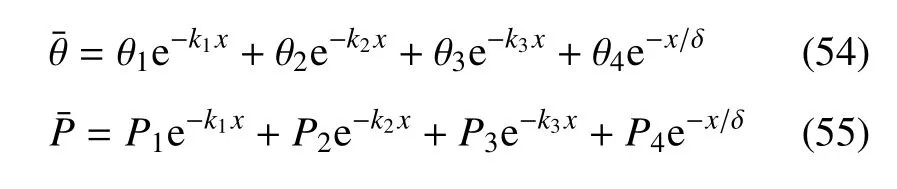
将式(49)、式(54)和式(55)代入式(38)和式(39),可以得到

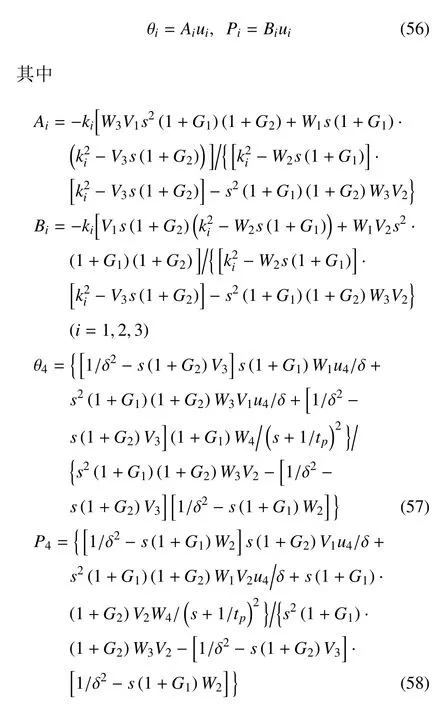
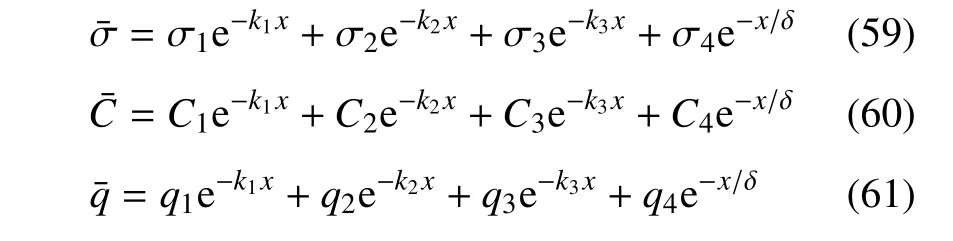
将温度、化学势和位移的解代入式(40)～式(42),可以得到

至此,得到了所有物理量在拉氏域中的解.

3 拉普拉斯数值反变换

为了将所求得的物理量从拉氏域转换到时间域中,还需进行拉普拉斯反变换.由于拉氏域中所得结果的复杂性,不便求其解析解,而应用数值计算的方法可以将求解过程简化.本文中,采用Brancik[33]提出的Matlab 程序进行拉普拉斯数值反变换.

4 模型验证及算例分析

考虑材料的记忆依赖效应和空间非局部效应,且边界面受非高斯激光脉冲加热和化学势冲击联合作用的半无限大薄板,其瞬态响应与时间t、非局部参数e0a、热时间迟滞因子ω1、扩散时间迟滞因子ω2、热核函数K1(t-ξ) 以及扩散核函数K2(t-ξ) 有关.本文重点研究非局部参数、热时间迟滞因子和扩散时间迟滞因子的变化对结构温度、化学势、位移、应力和浓度的影响.分析中用到的常量如下λ=7.76×1010kg/m·s2,μ=3.86×1010kg/m·s2,κ=386 W/(m·K),D=8.5 × 10-9kg·s/m3,αc=1.98 × 10-4m3/kg,ρ=8954 kg/m3,αt=1.78×10-5K-1,CE=383.1 J/(kg·K),a=1.2 × 104m2/(s2·K),b=9.0 × 105m5/(kg·s2),T0=293 K,L0=1.0×105J/m2,Ra=0.5,δ=0.01 m,tp=2.0 ps.

以下分析中所述量均为无量纲量,无量纲化学势幅值P0=1.

4.1 模型验证

为验证所建模型的准确性,基于本文所建模型分析了边界受热和化学冲击时板的响应,并与L-S 广义热弹扩散理论所得结果进行比较,分析中,热核函数和扩散核函数均取为1.t=0.1 时刻模型取不同参数时板的温度分布如图2 所示.由理论可知,当所建模型的热时间迟滞因子ω1、扩散时间迟滞因子ω2及非局部参数e0a均趋近于0 时,所建模型将退化为L-S 模型.由图2 可知,当ω1,ω2和e0a的取值趋近于0 时,本文模型所得结果向L-S 模型结果靠近.如图中所示,当它们取0.001 时,本文结果几乎于L-S 结果重合.由此验证了本文模型的准确性.

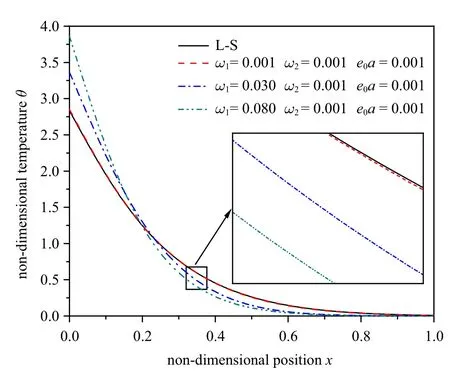
图2 记忆依赖非局部模型与L-S 模型的对比Fig.2 Comparison between memory-dependent nonlocal model and L-S model

4.2 非局部参数e0a 的影响

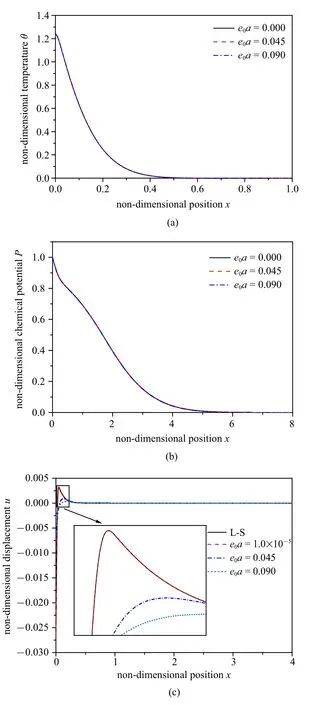
图3 随非局部参数的变化.(a)无量纲温度,(b)无量纲化学势,(c)无量纲位移,(d)无量纲应力,(e)无量纲浓度的分布规律Fig.3 The distributions of the non-dimensional temperature(a),chemical potential(b),displacement(c),stress(d)and concentration(e)with different nonlocal parameters

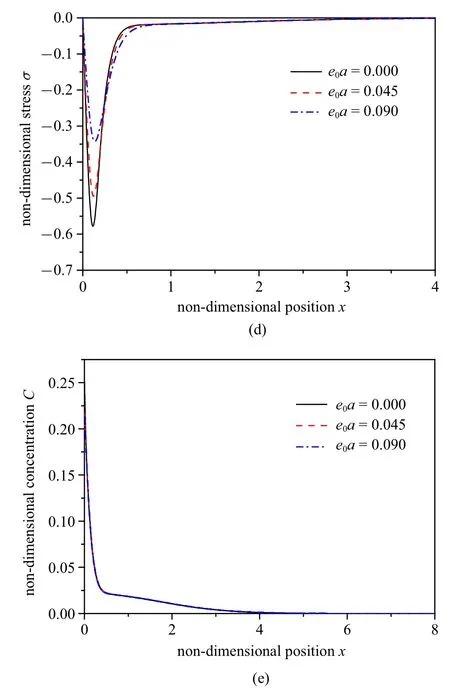
图3 随非局部参数的变化.(a)无量纲温度,(b)无量纲化学势,(c)无量纲位移,(d)无量纲应力,(e)无量纲浓度的分布规律(续)Fig.3 The distributions of the non-dimensional temperature(a),chemical potential(b),displacement(c),stress(d)and concentration(e)with different nonlocal parameters(continued)

研究非局部参数e0a的变化对温度、化学势、位移、应力和浓度分布规律的影响.在计算中,非局部参数分别取:e0a=0,e0a=0.045 和e0a=0.09,时间、热时间迟滞因子、扩散时间迟滞因子、热核函数和扩散核函数的取值分别为:t=0.05,ω1=0.02,ω2=0.02,K1(t-ξ)=1 和K2(t-ξ)=1.得到的结果如图3 所示.

从图3 可以看出:非局部参数取不同值时,位移和应力图像变化显著,而温度、化学势和浓度图像几乎不受非局部参数的影响.这是由于:非局部参数表征的是空间非局部效应,即它对本构方程影响显著,对传热和传质方程影响较小,而结构中的温度和化学势是由热传导方程和扩散方程控制的,故非局部参数的变化对位移和应力的影响显著,对温度、化学势和浓度的影响不显著.

由图3(c) 可知,位移的峰值随非局部参数的增大而减小,在靠近边界处,位移的最大值随非局部参数的增大而减小.当e0a的取值为小量(1.0×10-5)时,记忆依赖非局部模型与L-S 模型的位移曲线接近,此结论与理论预测一致,可验证本文模型的准确性.由图3(d) 可知,应力峰值的绝对值随非局部参数的增大而减小.图3(e)表明:温度达到零值前浓度的减小速率远远大于温度达到零值后浓度的减小速率.

4.3 热时间迟滞因子ω1 的影响

研究热时间迟滞因子ω1的变化对温度、化学势、位移、应力和浓度分布规律的影响.在计算中,热时间迟滞因子分别取:ω1=0.02,ω1=0.05 和ω1=0.08,时间、非局部参数、扩散时间迟滞因子、热核函数和扩散核函数的取值分别为:t=0.1,e0a=0,ω2=0.02,K1(t-ξ)=1 和K2(t-ξ)=1.得到的结果如图4 所示.

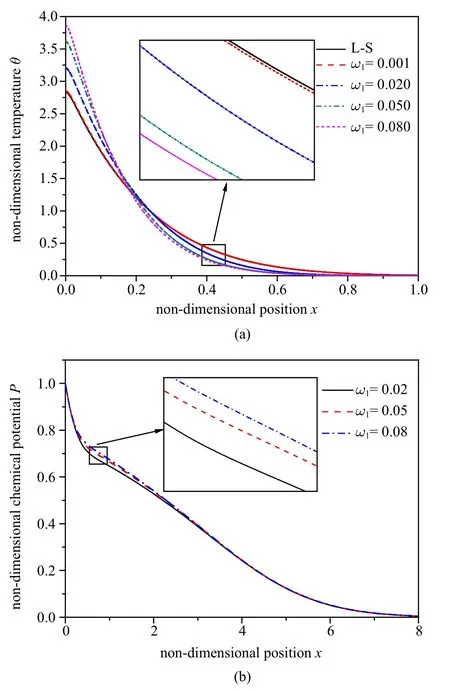
图4 随热时间迟滞因子的变化.(a)无量纲温度,(b)无量纲化学势,(c)无量纲位移,(d)无量纲应力,(e)无量纲浓度的分布规律Fig.4 The distributions of the non-dimensional temperature(a),chemical potential(b),displacement(c),stress(d)and concentration(e)under different thermal time delay factors

图4 随热时间迟滞因子的变化.(a)无量纲温度,(b)无量纲化学势,(c)无量纲位移,(d)无量纲应力,(e)无量纲浓度的分布规律(续)Fig.4 The distributions of the non-dimensional temperature(a),chemical potential(b),displacement(c),stress(d)and concentration(e)under different thermal time delay factors(continued)

由图4(a) 可知,温度在靠近边界处随热时间迟滞因子的增大而增大,在x=0.15 直至热弹波传播至零的过程中,温度随热时间迟滞因子的增大而减小.当ω1的取值为小量(0.001)时,记忆依赖非局部模型与L-S 模型的温度曲线接近,此结论与理论预测一致,可验证本文模型的准确性.图4(b)表明:化学势随热时间迟滞因子的增大而增大.由图4(c) 和图4(d)可知,位移峰值和应力峰值的绝对值均随热时间迟滞因子的增大而增大,在靠近边界处,位移的最大值随热时间迟滞因子的增大而增大.图4(e)表明:浓度随热时间迟滞因子的增大而减小.

4.4 扩散时间迟滞因子ω2 的影响

研究扩散时间迟滞因子ω2的变化对温度、化学势、位移、应力和浓度分布规律的影响.在计算中,扩散时间迟滞因子分别取:ω2=0.02,ω2=0.05 和ω2=0.08,时间、非局部参数、热时间迟滞因子、热核函数和扩散核函数的取值分别为:t=0.1,e0a=0,ω1=0.02,K1(t-ξ)=1 和K2(t-ξ)=1.得到的结果如图5 所示.

比较图5(a) 和图4(b) 可知,随热时间迟滞因子ω1的变化,化学势图像变化显著,随扩散时间迟滞因子ω2的变化,温度图像几乎重合,此现象表明:传热对传质过程影响显著,而传质对传热过程影响甚微.由图5(b)可知,扩散时间迟滞因子越小,扩散波传播的距离越远,其原因是:迟滞时间越短,意味着过去态越接近于现在状态,即时间越长,波传播的距离就越远.当ω2的取值为小量(0.001)时,记忆依赖非局部模型与L-S 模型的化学势曲线接近,此结论与理论预测一致,可验证本文模型的准确性.图5(c)、图5(d)和图5(e) 表明:位移峰值随扩散时间迟滞因子的增大而增大,在靠近边界处,位移最大值随扩散时间迟滞因子的增大而增大; 应力峰值的绝对值和浓度随扩散时间迟滞因子的增大而减小.

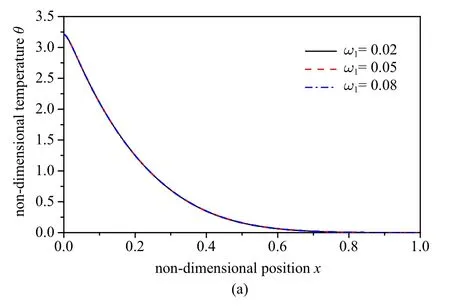
图5 随扩散时间迟滞因子的变化.(a)无量纲温度,(b)无量纲化学势,(c)无量纲位移,(d)无量纲应力,(e)无量纲浓度的分布规律Fig.5 The distributions of the non-dimensional temperature(a),chemical potential(b),displacement(c),stress(d)and concentration(e)under different diffusion time delay factors

图5 随扩散时间迟滞因子的变化.(a)无量纲温度,(b)无量纲化学势,(c)无量纲位移,(d)无量纲应力,(e)无量纲浓度的分布规律(续)Fig.5 The distributions of the non-dimensional temperature(a),chemical potential(b),displacement(c),stress(d)and concentration(e)under different diffusion time delay factors(continued)