磁-电-弹性半空间在轴对称热载荷作用下的三维问题研究1)
2020-11-03胡克强高存法仲政ChenZengtao
胡克强 高存法 仲政 Chen Zengtao
*(南京航空航天大学机械结构强度与振动国家重点实验室,南京 210016)
†(哈尔滨工业大学(深圳)理学院,深圳 518055)
**(Department of Mechanical Engineering,University of Alberta,Edmonton,AB,T6G 2G8,Canada)
引言
磁-电-弹性材料是一种同时具有压电压磁磁电耦合效应的复合材料,这种材料在工程结构中,尤其是在智能材料和结构系统中,有越来越广泛的应用.磁-电-弹性材料所固有的力电磁耦合特性使它们成为智能结构中传感与执行元件的首选材料,广泛应用于传感器、执行器、滤波器、换能器和其他智能器件,在能量转换系统中有着非常可观的潜在的应用前景[1-8].由于这些智能器件通常在复杂的力、电、磁和热耦合载荷环境下工作,因此对磁-电-弹性材料在多场耦合环境下的响应问题研究具有重要的意义.
近年来,关于磁-电-弹性材料力学问题的研究备受关注.Wang 等[9]推出了各向异性磁-电-弹性半空间在圆周方向载荷作用下的解析解.利用推广的Stroh 公式和坐标变换技术,Qin[10]求得了磁-电-弹性介质中含有任意方向半平面或双材料界面时的Green 函数解.利用积分变换和奇异积分方程方法,Hu 等[11]研究了磁-电-弹性和正交各向异性半空间中的界面裂纹问题,发现裂纹尖端的振荡奇异性或非振荡奇异性取决于双材料的特定材料属性组合.段淑敏等[12]用奇异积分方程法求解了磁-电-弹性材料与加层间的界面裂纹在反平面剪切冲击载荷和面内电磁冲击载荷作用下的动态响应问题,讨论了载荷、材料及几何参数对能量释放率的影响.Ma等[13]用扩展有限元法分析了磁-电-弹性双材料界面裂纹的静态断裂和多场耦合效应.Yang 和Li[14]通过考虑表面效应并利用Kirchhoff薄板理论,获得了纳米尺度圆盘状磁-电-弹性薄板弯曲和自由振动的解析解.
鉴于磁-电-弹性材料和结构通常会用在磁场、电场和温度场等多场耦合的载荷环境中,而其性能通常会受到温度载荷显著的影响,因此有必要对其热效应进行深入的研究[15].Hou 等[16]求得了各向同性磁-电-弹性材料中的二维形式的通解和基本解.通过弓入5 个调和函数,Chen 等[17]推导出了横观各向同性磁-电-热弹性体的一般解并得到了各耦合场的表达式.Carman 等[18]提出了一个含有保守非线性的磁-电-弹性材料中的微观机械模型.利用微观机械方法可以对完全耦合的磁-电-热弹性多相复合材料的性能进行系统的分析[19-20].Ke 和Wang[21]基于非局部理论和Kirchhoff板理论研究了磁-电-弹性纳米板的自由振动,发现其固有频率对于力、电和磁载荷很敏感但对热载荷不敏感.田晓耕和沈亚鹏[22]讨论并综述了磁-电多场耦合的广义电磁热弹性耦合问题方面的研究以及计及扩散效应和黏弹性效应的广义热弹性理论的发展.He 等[23]研究了无限长空心圆柱体中的广义电磁热弹性问题.Ootao 和Tanigama[24]研究了多层磁-电-热弹性板条在非稳定及非均匀热载荷作用下的动态响应.Karimi和Shahidi[25]利用非局部理论研究了磁-电-弹性纳米板在外加磁势、面内剪切和热载荷作用时的自由振动及表面效应.Gao 等[26]根据广义Stroh 公式研究了完全耦合的磁-电-弹性介质中的共线电渗透型裂纹问题并给出了在远场均匀热流作用时磁-电-弹性场强度因子的简洁表达式.利用积分方程法,Niraula 和Wang[27]求得了磁-电-弹性介质中的圆币型裂纹在均匀热流作用下的精确解.Li 等[28]求得了具有横观各向同性性质的无限大热-磁-电-弹性介质中的圆币型裂纹的三维基本解.Zhao 等[29-30]用扩展的位移间断边界积分方程法分析了三维横观各向同性热-磁-电-弹性双材料中任意形状的界面裂纹问题并讨论了电-磁场边界条件对各个场强度因子的影响.
从检索到的相关文献资料来看,现有的工作主要集中在求解无限大磁-电-弹性体中的力学问题或者相应的热载荷是作用在全部边界上的情形,而考虑边界的影响以及局部范围内分布载荷的作用则更具有实际意义.本文利用积分变换方法推导并求解了磁-电-弹性半空间在边界上作用轴对称温度载荷时的热传导和控制方程,得到了磁-电-弹性半空间中的温度场、应力、电位移和磁通量的解析解.本文结果对磁-电-弹性材料在热环境中的应用具有重要的指导意义.
1 基本公式
考虑一个横观各向同性的磁-电-弹性材料,其极化方向沿z轴方向,各向同性平面为xy平面,如图1 所示.对于轴对称问题,线性磁-电-弹性介质的本构方程为


其中,场变量为r和的z函数,与角度θ 无关;ur和uz分别是径向和轴向弹性位移的分量;φ 和φ 分别是电势和磁势;σrr,σθθ,σzz,σrz为应力张量的分量;Dr和Dz为电位移的分量;Br和Bz为磁通量的分量;c11,c12,c13,c33,c44为弹性模量;e15,e31,e33为压电常数;ε11,ε33为介电常数;d11,d33为电磁常数;μ11,μ33为磁渗透系数; βj(j=1,2,...,5) 是热应力系数; ΔT是温度变化量; [ ]′表示矩阵的转置; ()表示对相应坐标的求偏导.
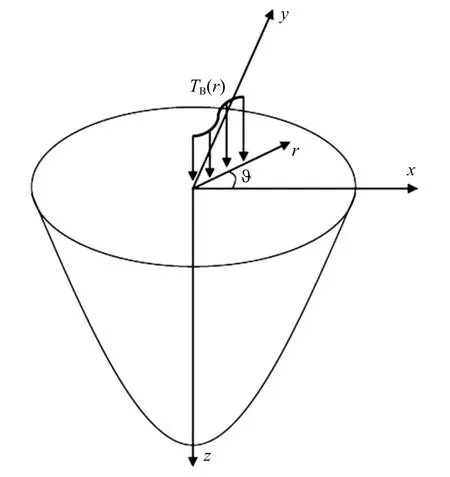
图1 轴对称热载荷作用下的磁-电-弹性半空间Fig.1 A magnetoelectroelastic half-space under axisymmetric thermal loading
电场Ej(j=r,z)和磁场Hj(j=r,z)可以分别由电势和磁势的偏导数表示为
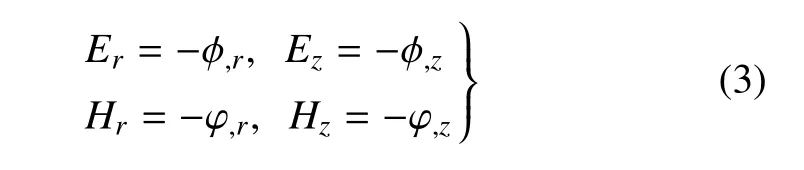
若不计体力及自由电荷,平衡方程可以表示为
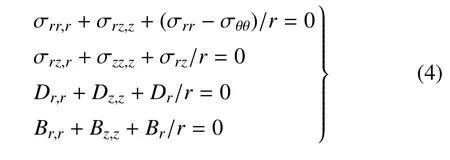
将方程(1)和(2)代入以上方程可以得到关于位移ur,uz,电势φ 和磁势φ 的控制方程如下

2 问题求解
考虑一个在其边界表面上作用有轴对称热载荷的磁-电-弹性半空间,如图1 所示.采用柱坐标(r,θ,z),并假定极化方向沿z轴方向;TB(r)是一个定义在圆域(r≤a,z=0)内的轴对称函数.
横观各向同性材料在轴对称条件下的稳态热传导方程为

其中,T=T(r,z) 是介质中的温度分布函数,kr和kz分别为r和z方向的热传导系数.应用Hankel 变换可以得到温度的表达式为

其中,A(ξ)为待求函数,A0是一个可以由远场边界条件确定的常数,J0()是第一类零阶Bessel 函数,系数λ 定义为

假设无穷远处的温度为一有限值TI并且作用于磁-电-弹性介质边界上有界区域内的温度为TB,即
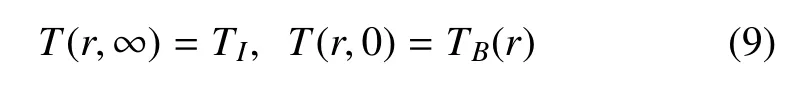
则A0和A(ξ)可以表示为

将方程(10) 代入方程(7) 可以得到温度场的表达式为

温度变化可以表示为

对方程(5)做Hankel 变换,可以得到弹性位移,电势和磁势的通解如下
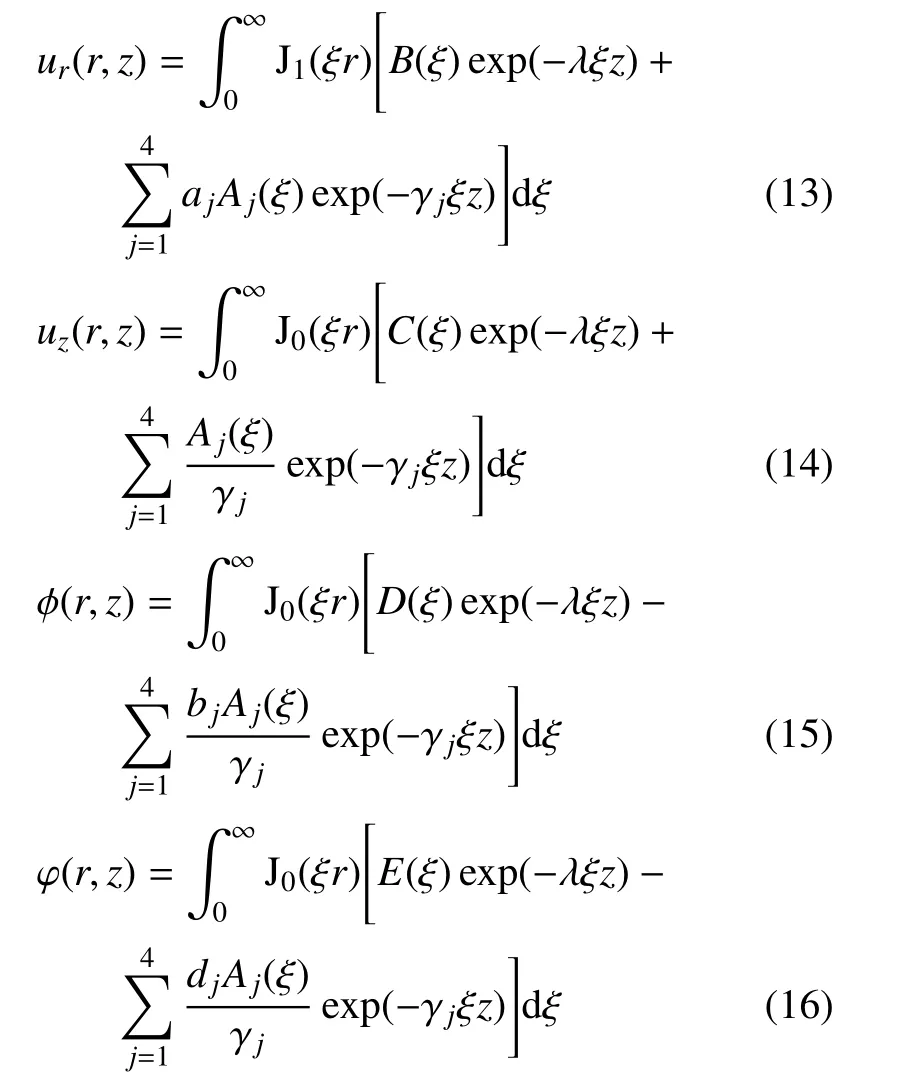
其中,Aj(ξ) (j=1,2,3,4),B(ξ),C(ξ),D(ξ),E(ξ) 为待求的未知函数,aj,bj,dj,(j=1,2,3,4) 是与材料系数相关的已知的系数,见附录;J1()是第一类的一阶Bessel 函数,γj(j=1,2,3,4) 为以下特征方程的特征根
其中,|M|表示矩阵M的行列式值.这里需要指出的是,八阶特征方程(17)有8 个特征根成对出现,每一对大小相同符号相反,复根以共轭形式成对出现.在式(13)~式(16)中,取特征根γj(j=1,2,3,4)的实部为正,以确保稳定系统的内能正定[31-32].
利用本构方程,可以得到应力,电位移及磁通量的各个分量为
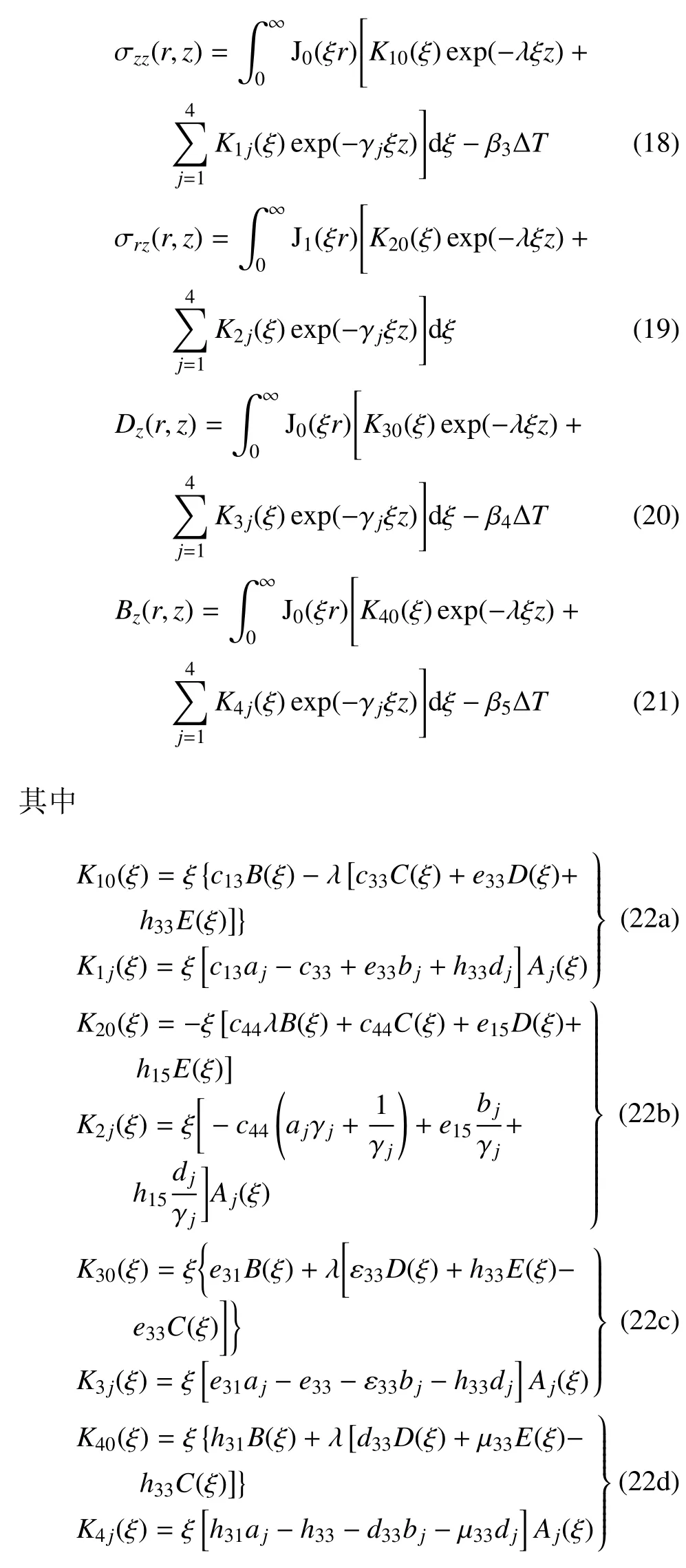
当在半无限大体的表面只作用有热载荷作用时,磁-电-弹性半空间表面上电、磁和机械边界条件为
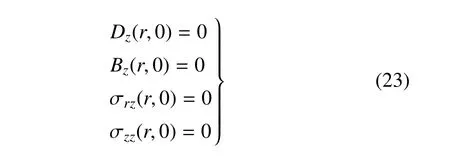
将方程(18)~(21) 代入方程(23),可以得到以下关系式

未知函数B(ξ),C(ξ),D(ξ),E(ξ) 可以由函数A(ξ) 表示为
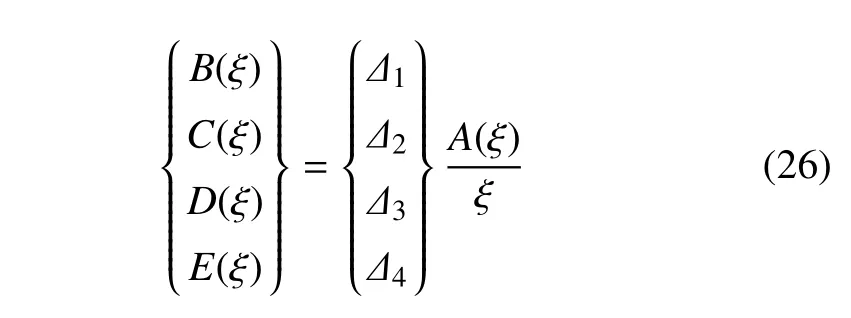
其中,Δj(j=1,2,3,4)的表达式在附录中给出.
Yj(j=1,2,3,4)可以表示为A(ξ)的函数
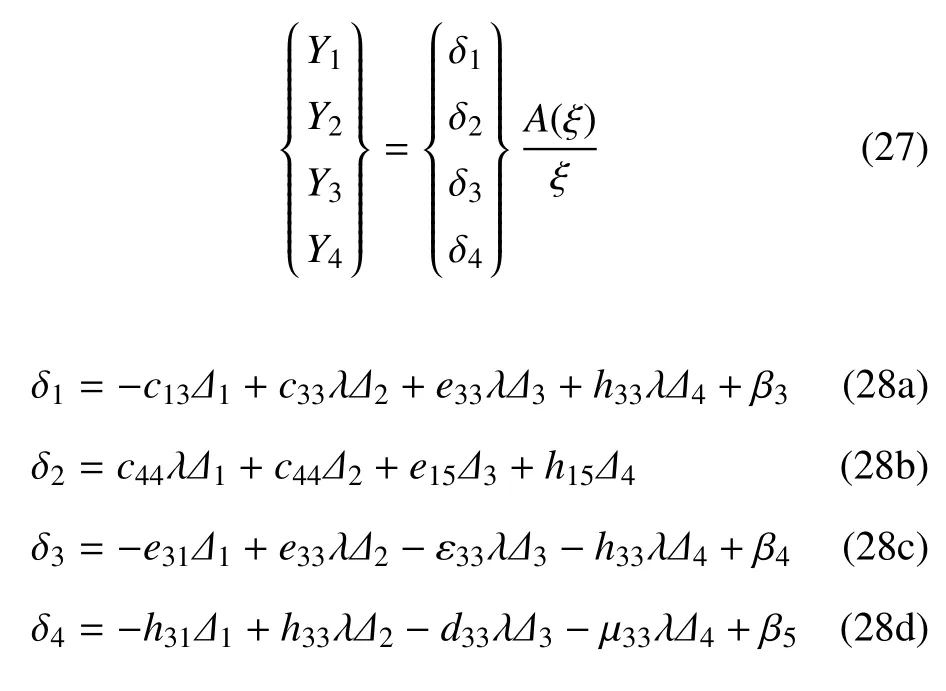
Aj(ξ)(j=1,2,3,4)与A(ξ)的关系为

求解以上方程可得

其中,Ωj(j=1,2,3,4)在附录中给出.
本文考虑如下定常相对温度作用在磁-电-弹性半空间表面上一个圆域上的情形
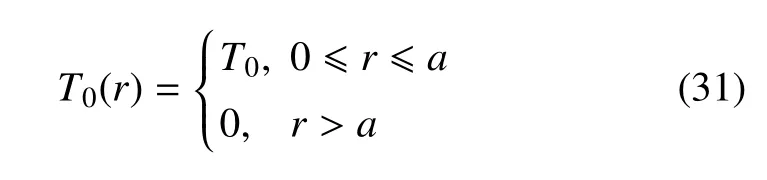
需要指出的是,T0是作用在圆域上的温度与圆域外的温度的相对值,而所考查的半空间中的磁-电-弹性场的变化与T0有关.
将方程(31)代入方程(10)可以得到

温度场的积分表达式如方程(7)所示,利用关系式(26)和式(30),可以得到位移、电势、磁势、应力、电位移和磁通量的解析形式的表达式.在此略去具体的细节,应力、电位移和磁通量的分量可以表示为


其中,系数Vk(k=1,2,...,6),Ej,Fj,Gj,Hj,Kj,Lj(j=1,2,3,4)在附录中给出,积分算子Ij(λ)(j=1,2)定义为
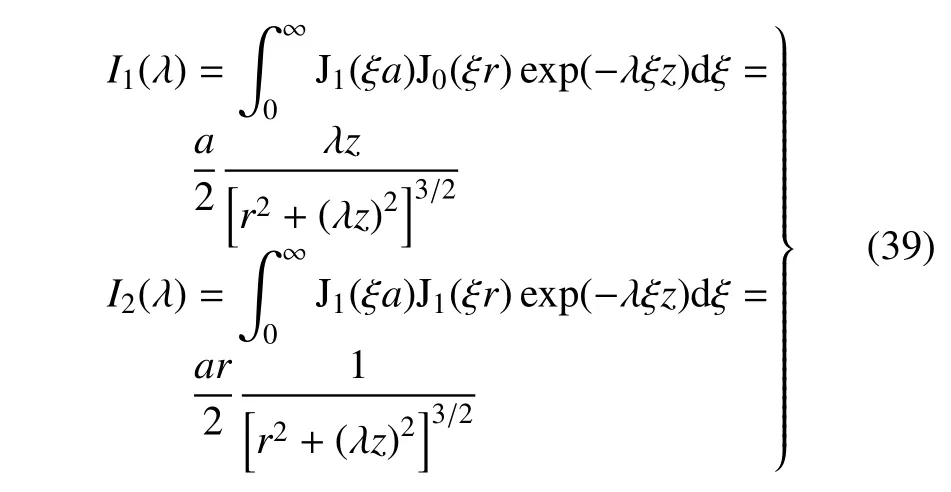
常数βj(j=1,2,3,4,5)可表示为
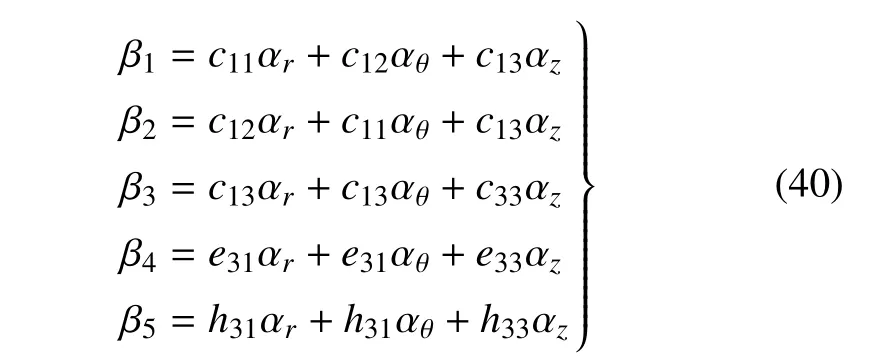
其中,αi(i=r,θ,z)为热膨胀系数.
由以上所得到的磁、电、热弹性场的解析表达式可知,对于在任意区域作用任意温度载荷的情形,本文的结果可以作为一个基本解,在线弹性和小变形范围内利用叠加原理可以得到一般温度载荷情形的解.需要指出的是,由于解的表达式中含有无限积分项,在不能获得精确积分结果的情况下,数值积分可能会产生一定的误差.
3 数值计算及分析
在数值计算中,不失一般性,我们取一具有完全的机械、电和磁场耦合作用的横观各向同性性质的磁-电-弹性材料-复合材料BaTiO3-CoFe2O4,其材料常数为[31]

对于以z轴为极化方向的横观各向同性材料,径向和切向的热膨胀系数相同,即αr=αθ.因此,由方程(40)可知β1=β2.在以下的数值计算中,热膨胀系数假定为αr=αz=7.0×10-6K-1,圆域内的相对温度值假设为T0=100 K.
图2 给出了磁-电-弹性半空间中的无量纲化的正应力的分布.图中显示最大应力发生在沿-轴方向距离半空间边界约z≈1.3a的位置.可以推断当温度载荷作用的圆域半径增大时(a增大),最大应力发生的位置会远离半无限大体的边界,即最大应力会发生在更深处; 反之当温度载荷作用的圆域半径减小时(a减小),最大应力发生的位置会靠近半无限大体的边界,即最大应力会发生在靠近边界的位置.需要指出的是,在圆域外(r>a)的正应力很小.
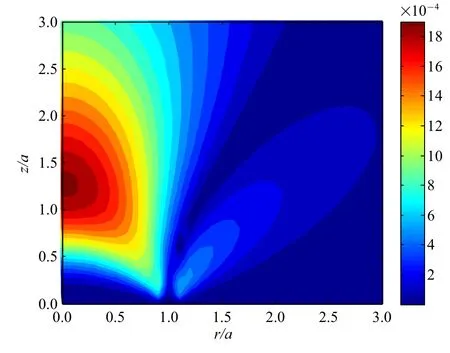
图2 正应力σzz/β3T0 的分布Fig.2 Distributions of the normalized stress σzz/β3T0
图3 显示了在圆域温度载荷作用下磁-电-弹性半空间中最大剪应力σrz/β3T0的分布.最大剪应力发生在靠近边界表面大约在圆形区域的边上(r≈a).在远离温度载荷作用区域(r>2a,z>a)时,剪应力变得相当小.

图3 剪应力σrz/β3ΔT 的分布Fig.3 Distributions of the shear stress σrz/β3ΔT
图4 给出了无量纲化的电场的分布,可以看出,电场在温度载荷作用的圆域内在边界表面附近有明显的强化.这一结果预示在高温载荷情形时,高温度区域可能会出现电击穿的情形.图5 显示了半无限大空间中磁场的分布,正的和负的磁场在不同的区域都得到了强化:负的磁场在z轴附近约的区域强化显著,而正的磁场在z≈0.1a,r=1.2a的区域得到了强化.
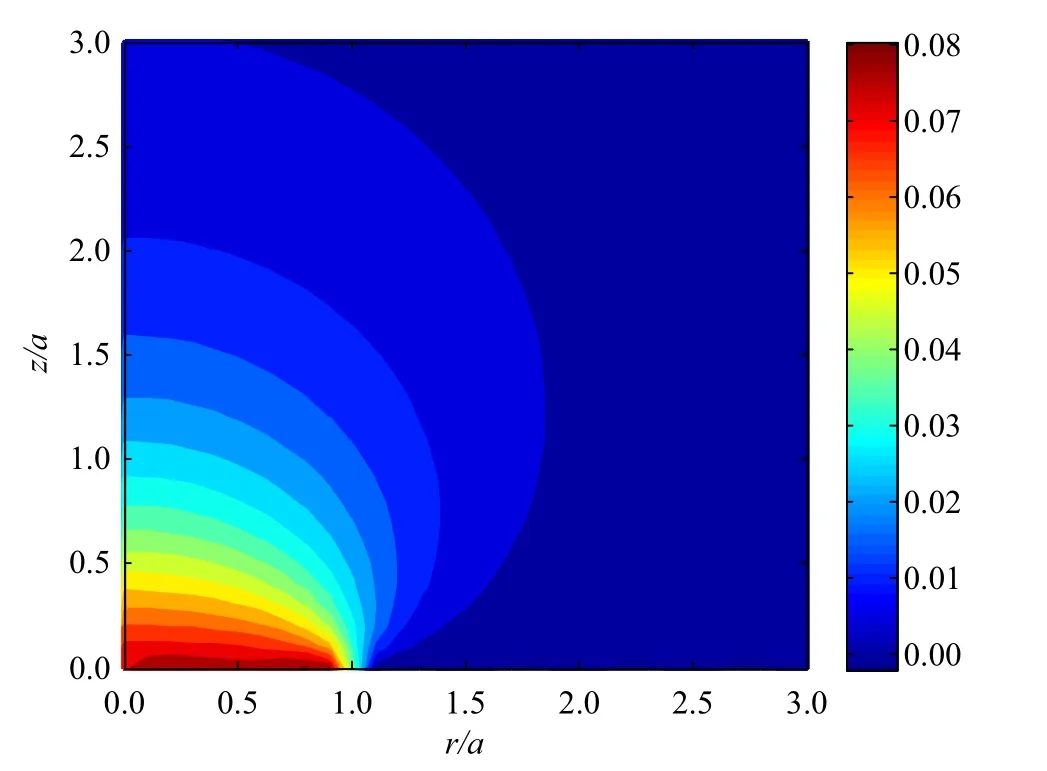
图4 电场e33Ez/β3ΔT 的分布Fig.4 Distributions of the normalized electric field e33Ez/β3ΔT

图5 磁场h33Hz/β3ΔT 的分布Fig.5 Distributions of the normalized magnetic field h33Hz/β3ΔT
4 结论
本文给出了磁-电-弹性半空间在轴对称温度载荷作用下的磁-电-热-弹性多场耦合的解析解.利用变换法成功求解了磁-电-弹性介质中的热传导方程和控制方程,得到了温度场分布的解析表达式,并进一步获得了应力,电位移和磁通量在半空间中的场分布.数值结果表明在温度载荷作用下应力,电位移和磁通量在各自特定的区域内会得到强化,磁-电-弹性场强化区域的强化程度跟温度载荷的大小和作用区域大小相关.本文结果对磁-电-弹性材料和结构的设计和应用具有重要的理论指导意义.
附 录
方程(13),方程(15)和(16)中的常数aj,bj,dj(j=1,2,3,4)定义为
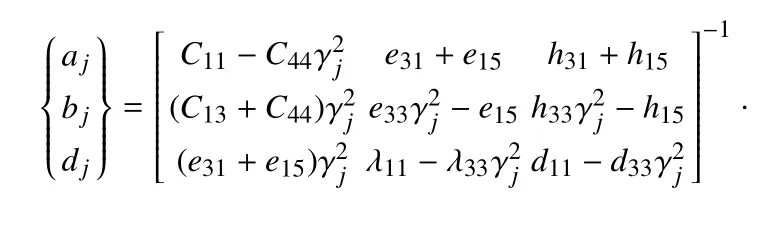
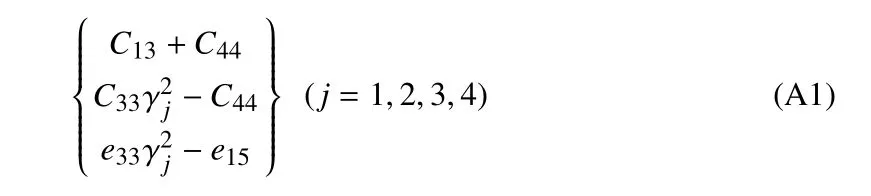
其中,γj(j=1,2,3) 为特征方程(17) 的特征根.在方程(26) 中Δj(j=1,2,3,4)定义为

在方程(30)中Ωj(j=1,2,3,4)定义为


其中分量Xi j(i,j=1,2,3,4)在方程(25)中定义.
方程(33)~(38)中的系数Vk(k=1,2,...,6)定义为

