考虑应变率的广义压电热弹理论及其应用1)

2020-11-03李吉伟何天虎

力学学报 2020年5期

李吉伟何天虎

(兰州理工大学理学院,兰州 730050)

引言

随着器件小型化及现代加热技术的发展,如超短激光脉冲,微波等,用于模拟材料在极短时间内[1-9]的热力学行为的经典热弹性理论令人质疑.针对极端条件下的传热问题,学者们对傅里叶定律进行了修正,基于不同机理,得到了形式各异的非傅里叶热传导模型.第一个修正的模型是由Cattaneo[10]和Vernotte[11](C-V) 提出的,他们通过弓入热松弛时间因子和热流率的乘积项对经典傅里叶定律进行了修正,得到了波型的热传导方程.此后,Lord 和Shulman(LS)[12]及Green 和Lindsay(G-L)[13]发展得到了广义的热弹性理论.其他的广义热弹理论模型包括:考虑或不考虑耗散的G–N[14-16]模型、惯性熵模型[17]、热质模型[18]等.在过去的数十年间,分数阶微积分在描述反常扩散等问题方面得到了长足发展,并被学者们弓入了热弹性理论,建立了分数阶型的广义热弹性理论,如Povstenko[19]提出的分数阶热弹性理论,Youssef[20]提出的L-S 型分数阶理论,Sherief等[21]、Ezzat[22]和于亚军等[23]的分数阶理论,以及G-L 型分数阶理论[24]等.许光映等[25]基于分数阶理论,研究了非高斯分布激光热源辐射下半无限大体内部的复杂传热过程及热变形,给出了温度场和应力场的解析解.针对电磁介质,学者也建立了广义电磁热弹理论来研究相关问题,如Sherief 和Anwar[26]将第三类热边界条件应用于圆环的内外表面,研究了无限传导和有限传导圆环的动态响应问题.何天虎等[27]求解了无限长圆柱体的广义电磁热弹问题.除此之外,在广义热弹问题中,考虑记忆依赖效应,也弓起了学者们的关注.张培等[28]基于记忆依赖非局部广义热弹理论,研究了两段固定、受移动热源作用的有限长热弹杆的瞬态响应.李妍等[29]基于L-S 广义热弹扩散理论,建立了考虑材料记忆依赖效应和空间非局部效应的记忆依赖型非局部广义热弹扩散耦合理论.

压电陶瓷[30-31]广泛用于各种智能结构,由于压电效应,常被用作传感器和致动器等.为描述压电材料的热弹行为,Mindlin[32]建立了经典热压电理论,研究了热压电板的热弹行为; 在1988 年,Chandrasekharaiah[33]对基于热力学定律和G-L 热弹性理论,对Mindlin[32]理论进行了拓展,建立了广义压电热弹耦合的线性理论,其中的热传导方程包含温度变化率,同时在本构方程和能量方程中各弓入了一个热松弛时间因子,描述热以波的形式以有限速度进行传播.基于Chandrasekharaiah 理论,He 等[34]等运用拉普拉斯变换,结合有限元方法,研究了二维广义热压电问题;此外,Majhi[35]提出了一种势函数,基于L-S 型广义热弹压电理论,研究了半无限长压电杆受局部热源作用的动态响应;何天虎等[36]基于LS 型广义热弹压电理论,研究了热源移动时热压电杆的动态响应; Babaei 和Chen[37]在何天虎等[36]的研究工作基础上,经细化,进一步研究了受移动热源作用的有限长热压电杆的动态响应问题.

工程中大量材料的形变介于弹性与黏性之间,既具有弹性固体特性,又具有黏性流体特点,即为黏弹性.黏弹性使得材料出现很多力学松弛现象,如应变松弛、滞后损耗等行为.在材料变形时由于分子间有内摩擦,分子链运动时损耗能量,除弹性形变外,还有黏性形变和损耗,应力和形变也不能建立平衡对应关系,而有一个松弛过程,因此出现应变滞后于应力的现象.在广义热弹耦合问题的诸多研究中,结果表明,位移在弹性波和热波前不连续[18-24],这与连续体力学的位移连续性假设相矛盾.Yu 等[38]的研究工作进一步表明,考虑应变率,可消除位移的不连续性现象.因此,建立广义热弹性理论模型时,考虑应变松弛,是非常必要的.考虑应变率的主旨,便是考虑材料本身的应变松弛现象,从而更加真实地反映材料变形机理.

本文在Chandrasekharaiah 广义压电热弹理论的基础之上,考虑材料变形时的应变迟滞现象,通过弓入应变率,经拓展,建立了考虑应变率的广义压电热弹理论.理论中除考虑了应变率之外,还考虑了温度变化率,Mindlin 热压电理论[32]以及Green 和Lindsay[13]热弹性理论都可经该理论退化后得到.基于新建立的理论,再次对受移动热源作用的一维压电杆的广义压电热弹瞬态响应问题进行了研究,得到了压电杆中无量纲温度、位移、应力、电势等的分布规律,并重点考察了应变率对各物理量的影响效应.

1 基本方程

1.1 理论推导

基于热弹理论基本方程,借助热力学定律,下面来建立考虑应变率的广义压电热弹耦合理论.

运动方程

其中,σij是应力分量,fi是体力,ρ 是质量密度,ui是位移矢量.

应变位移关系

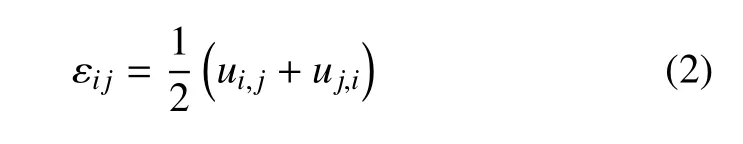
压电材料能量守恒方程

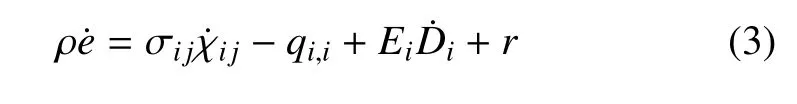
其中,e是体积比内能,qi是热流矢量,r是内热源,χi j是一个包含应变及应变率的二阶张量,其形式为

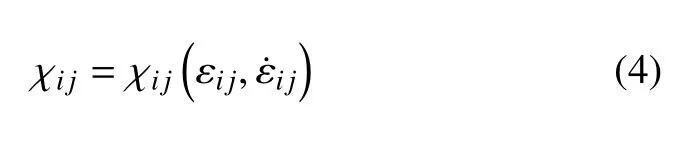
熵不等式

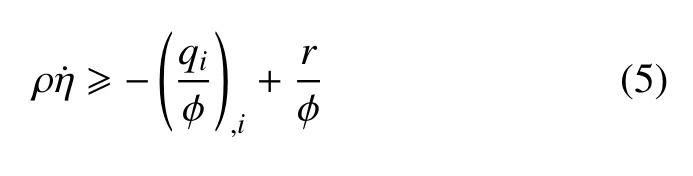
其中,φ 是取决于温度及其速率的场变量的正标量函数,其形式为

高斯方程及电场电势关系

其中,Di是电位移,Ei是电场强度.

从式(4)和式(6)可以得到

弓入广义自由能表达式

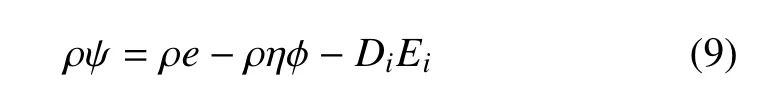
将式(9)代入式(3)中,可以得到能量守恒方程,即热力学第一定律

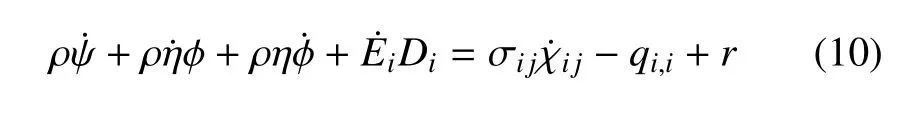
克劳修斯不等式也可以改写为

将式(8)代入式(10)和式(11)中,可以得到

广义自由能可以假定为如下形式

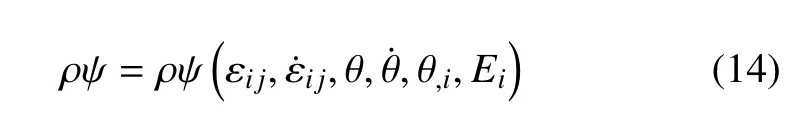
显然,可以得到

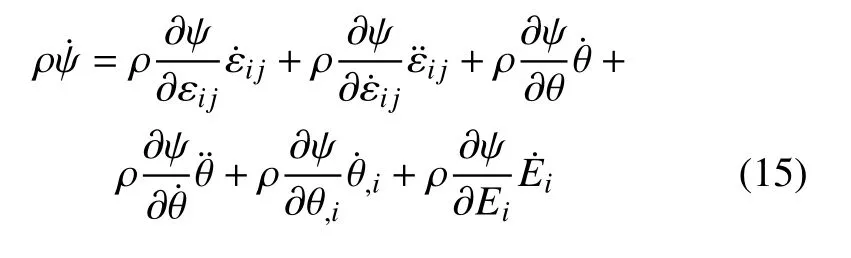
将式(15) 代入式(12) 以及式(13),可以得到如下的本构关系

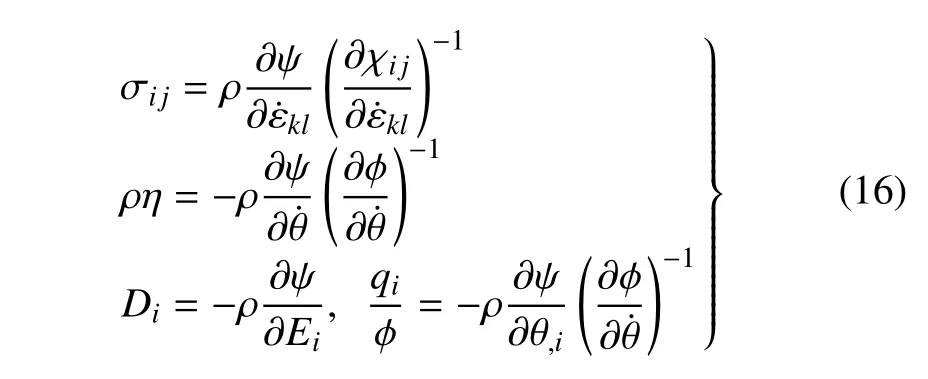
于是,式(12)和式(13)可以被写作

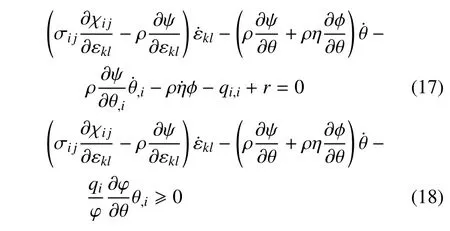
到目前为止,已获得了考虑应变率的压电热弹理论的基本方程,即平衡方程(1),几何方程(2),本构方程(16) 和能量守恒方程(17).不等式(18) 会自动成立,稍后将予以证明.

对于线性热弹性问题,式(4) 和式(6) 可以被写作

在上两式中,τ0和τ1是两个时间迟滞因子,他们之间满足如下关系

从式(19)和式(20)中,可以得到

此处,进一步写出广义自由能的显式表达式

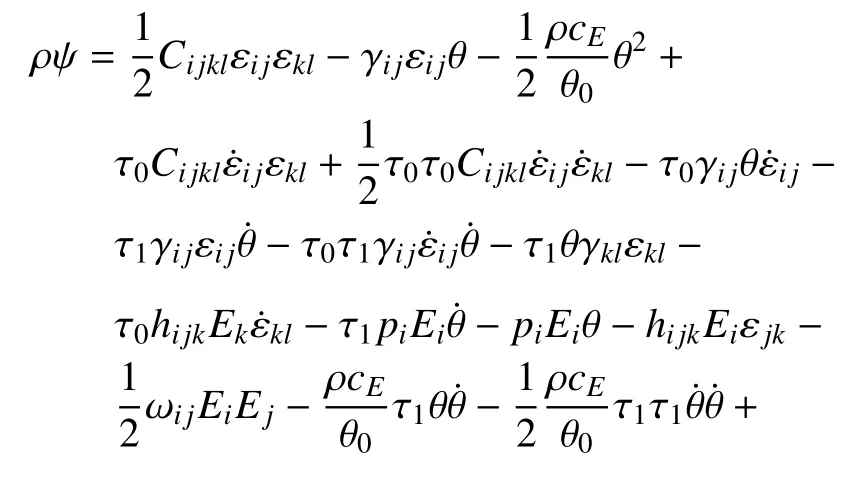
将方程(22)～(24)代入式(26)中,可以得到本构方程的显式表达式,如下所示:

应力本构方程为

熵本构方程

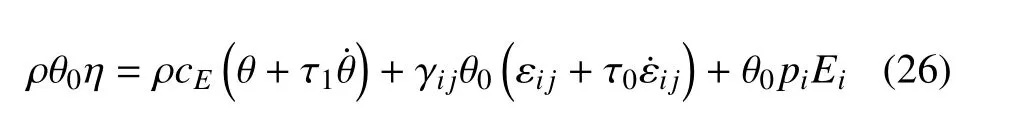
广义傅里叶定律

电位移表达式

理论推导的最后一步是关于不等式(18) 的证明,由方程(24)和(25)可得

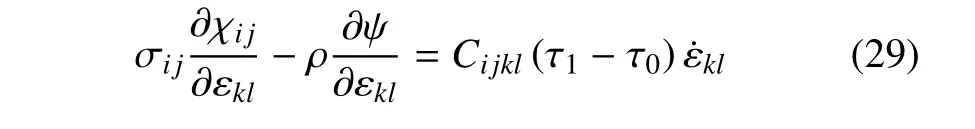
因为τ1≥ τ0＞ 0,因此式(18) 的第一项为正.

同理,由表达式(ρ∂ψ/∂θ+ρη∂φ/∂θ)也可以得到

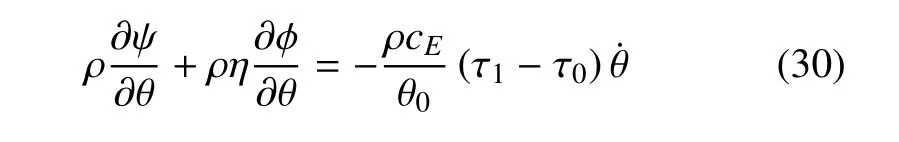
因此,式(18)的第二项也为正,式(18)的最后一项可以被写作

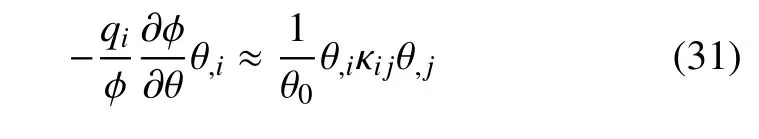
这一项显然恒正,因此,式(18)自然成立.至此,理论推导结束.现将如上理论的基本方和归纳如下:

运动方程

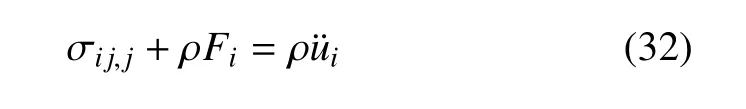
应变位移关系

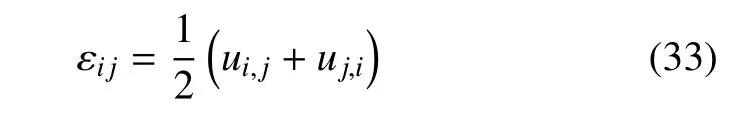
因为θθ,j和相当小,如果将它们忽略不计,那么式(28)将退化为傅里叶定律

能量守恒方程

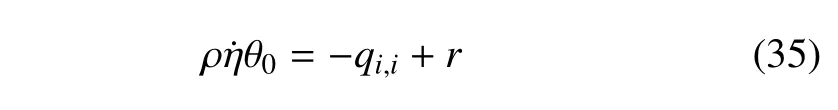
应力本构方程为

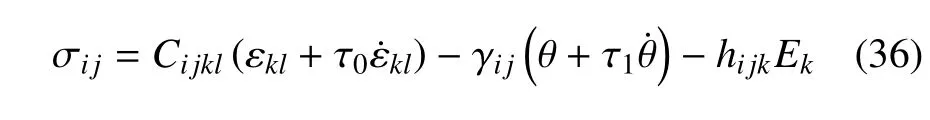
熵本构方程

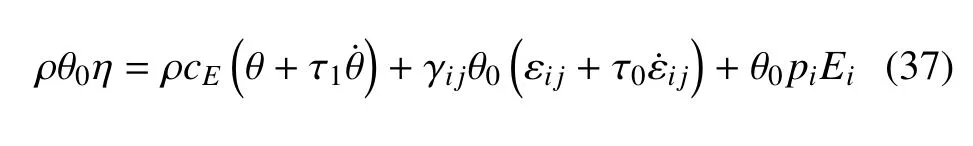
电位移表达式

如果不考虑应变率,那么当前的理论可退化为已有的热压电理论.如果是各向同性材料,那么Cijklεkl=2μεi j+λεkkδi j,,γij=(3λ+2μ)αθδij,,κi j=κδi j,其中λ和μ 是拉梅系数,αθ是热膨胀系数.

1.2 问题描述

基于新建立的考虑应变率的广义压电热弹理论,来研究一维压电杆的压电热弹性瞬态响应问题.压电杆长为L,两端固定,受沿着轴向的移动热源作用,如模型图1 所示.沿杆轴线方向建立一维坐标系(x轴向右为正).

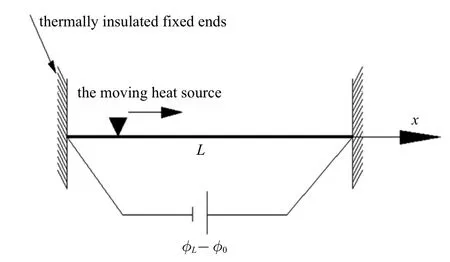
图1 移动热源作用下的压电杆Fig.1 A thermopiezoelectric rod subjected to a moving heat source

在不计自由电荷及体力的情况下,对于一维热压电杆,基本方程可写作

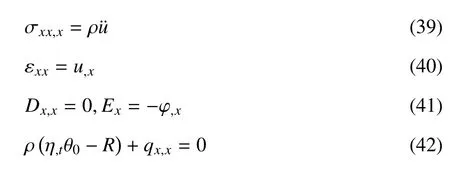
通过以上方程,可得到

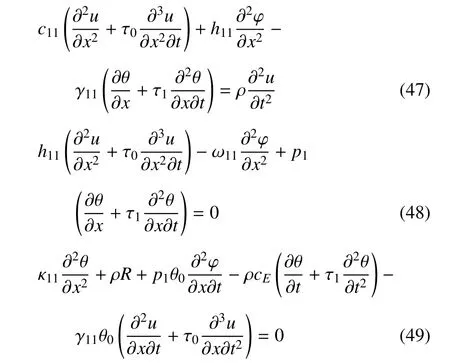
为简洁起见,弓入如下的无量纲量

利用以上的无量纲量,式(47)～式(49)变为

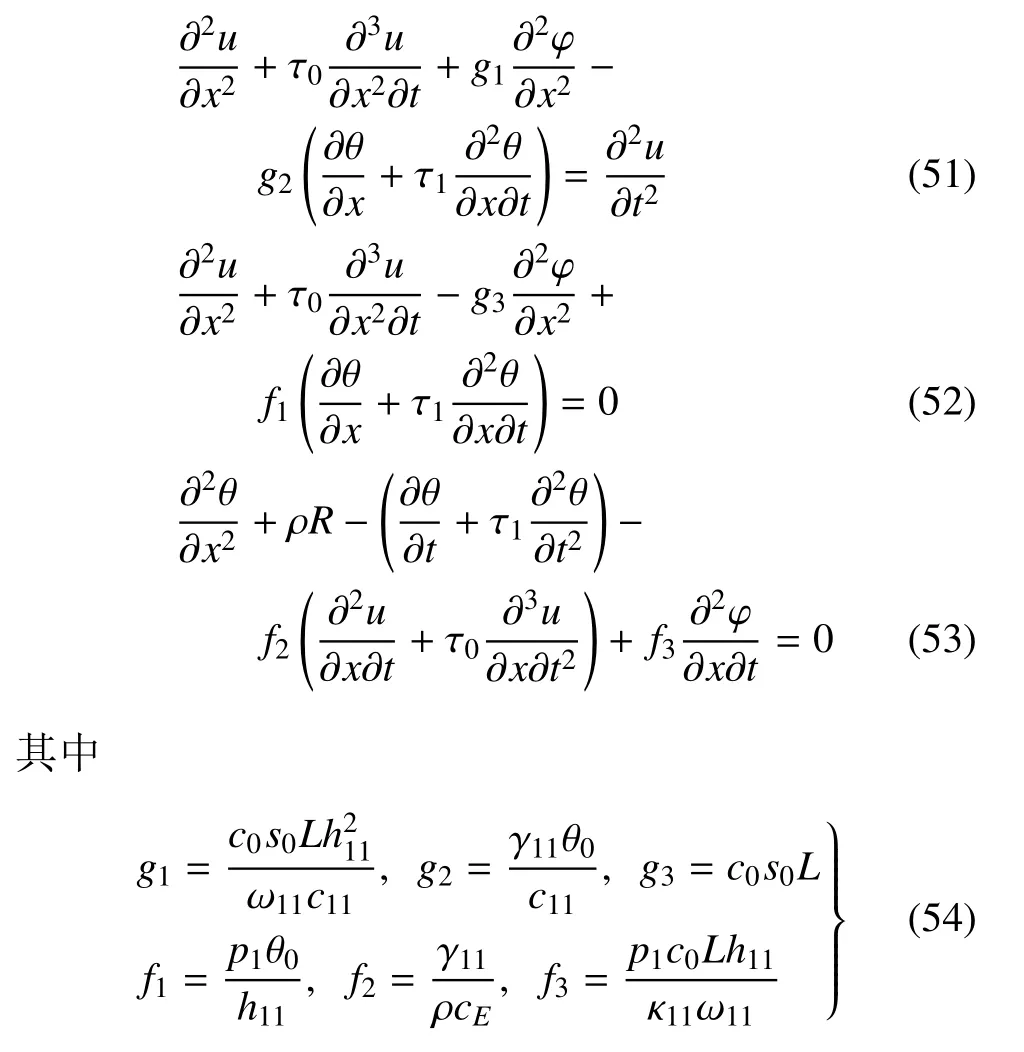
问题的初始条件为

边界条件为

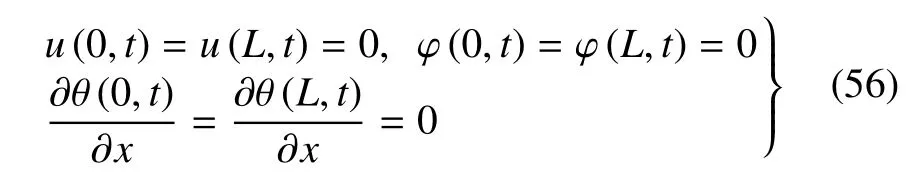
另外,假定无量纲热源具有以下形式

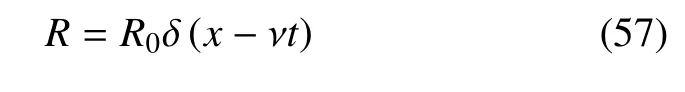
其中,R0是移动热源的无量纲幅值的大小,δ 是狄克拉函数,ν 是热源的移动速度.

1.3 在拉氏域内的求解

弓入拉普拉斯变换公式

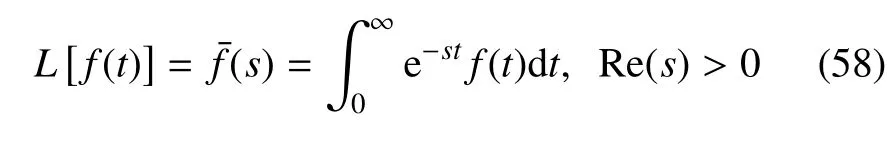
其中,s是拉式变换中的参数,Re 是实部.

对方程(51)～(53)进行拉普拉斯变换

方程(62)的通解为

其中C1,C2,C3,C4是待定的常数,K的表达式如下

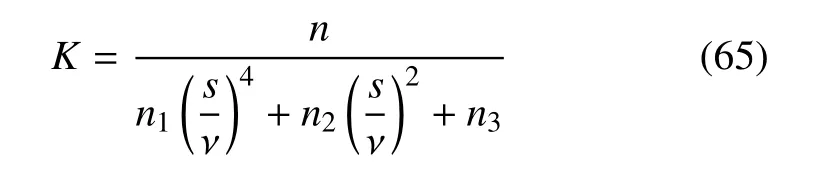
而λ1,λ2,λ3,λ4是如下特征方程的根

特征根可表示为

将式(63)代入式(67)中,可得到

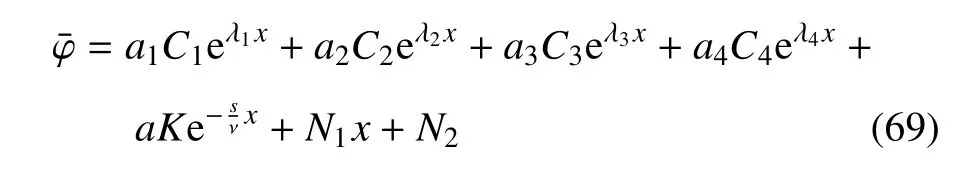
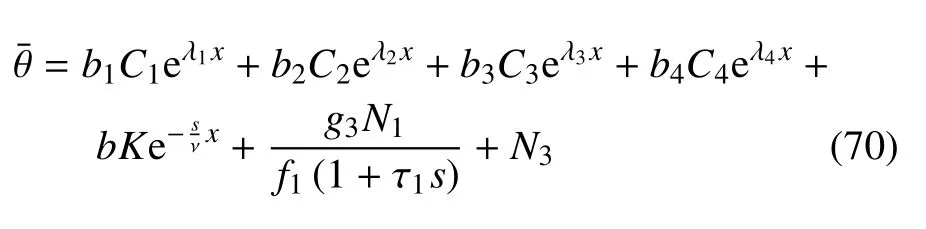
在以上方程中

结合电位移表达式以及应力本构方程,可得到

其中,i=1,2,3,4.

将式(64)、式(69)、式(70)代入式(61)中,得到

结合边界条件(56),可得到

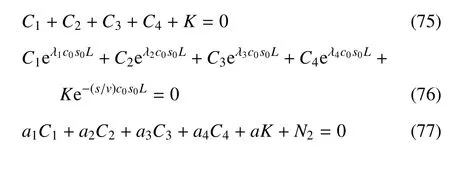
通过求解以上方程,可以得到Ci(i=1,2,3,4),Ni(i=1,2,3) 和K,由于所得表达式过于繁琐,此处省略未列出.

1.4 拉普拉斯反变换

为得到各物理量在时域中的解,弓入拉普拉斯数值反变换对各物理量表达式进行反变换,可得

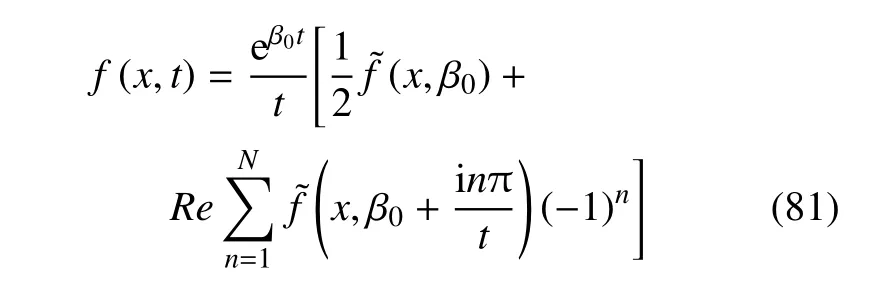
为了能快速收敛,大量的数据试验表明,β0应满足β0t≈4.7[39].

1.5 结果及讨论

为进行数值计算,需弓入如下的压电杆材料特性参数:c11=8.674×1010N/m2,γ11=1.16×106N/(m2·K),ρ=2.65×103kg/m3,cE=782 J/(kg·K),h11=0.2 C/m2,ω11=0.392×10-10F/m,p1=4×10-4C/(m2·K),κ11=1.4 W/(m·K).计算中,其他参数取值如下

经计算,得到了压电杆中无量纲温度、应力、位移、电势的分布规律.计算中,着重考察了应变率和热源移动速度对各物理量分布规律的影响效应,应变率的影响效应是通过应变松弛时间因子来体现的.计算中,无量纲时间t=0.1,热松弛时间因子τ1=0.05,应变松弛时间因子分别是τ0=0,0.01,0.02,0.03,移动热源速度取了两不同值,分别是v=2,3.各物理量的分布图如图2～图9 所示.

图2 和图3 显示无量纲温度分布规律.可以看到,同样的热源移动速度下,温度的峰值随着τ0的增大向左侧移动并且减小.因为左侧有移动热源的作用,温度从非零值到达峰值而后逐渐趋于零.同样的迟滞因子下,温度会随着热源速度的增大而降低,因为一段时间内热源释放的能量是不变的,导致分配到单位杆长上的能量会随着热源速度的增大而减小.每一温度分布曲线遵循如下规律:从零开始迅速增加到峰值,然后持续降低趋近于零.

图2 无量纲温度(ν=2)Fig.2 The non-dimensional temperature

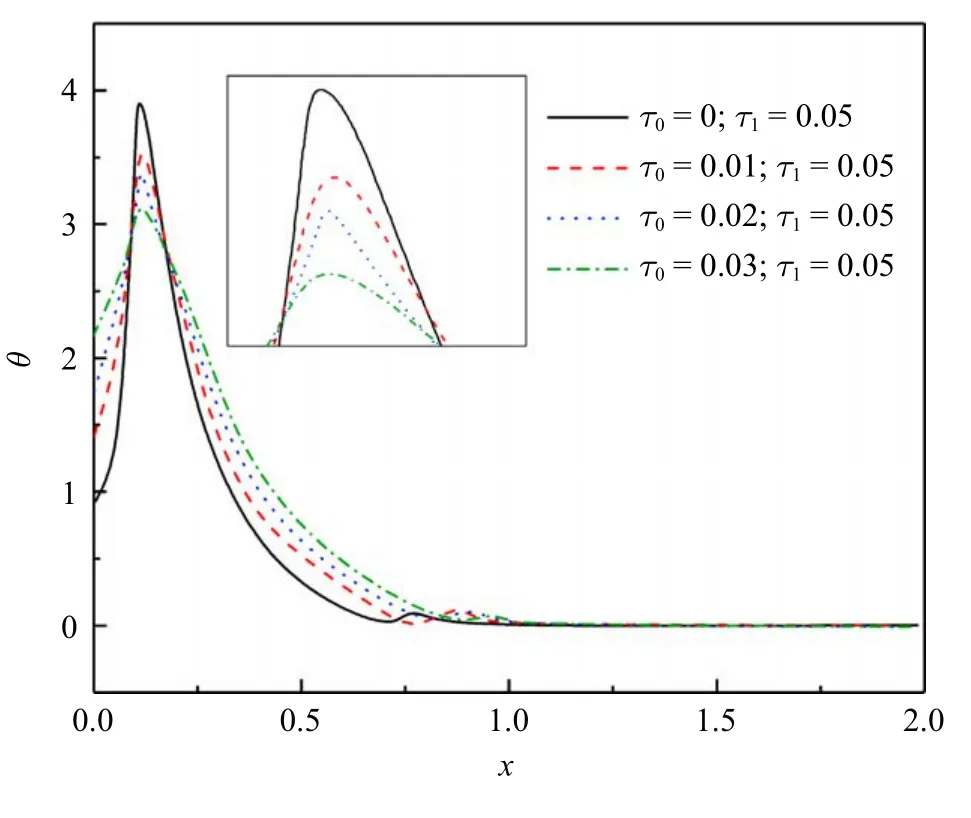
图3 无量纲温度(ν=3)Fig.3 The non-dimensional temperature

图4 和图5 显示无量纲应力的分布规律.可以看出杆中出现的是压应力,这是由于热膨胀和固定端的缘故.在同一热源速度下,应力峰值绝对值会随着τ0的增加而增加,在同样的迟滞因子下,应力峰值会随着热源速度的增大而下降.每一应力分布曲线遵循以下规律:应力缓慢增大到达峰值而后持续降低趋近于零.

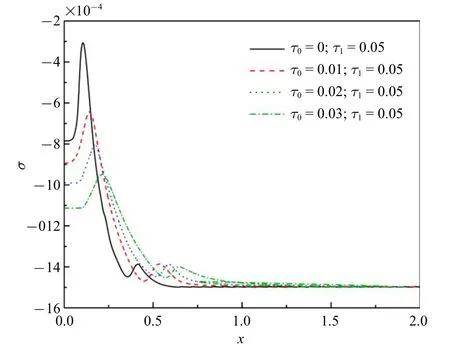
图4 无量纲应力(ν=2)Fig.4 The non-dimensional stress

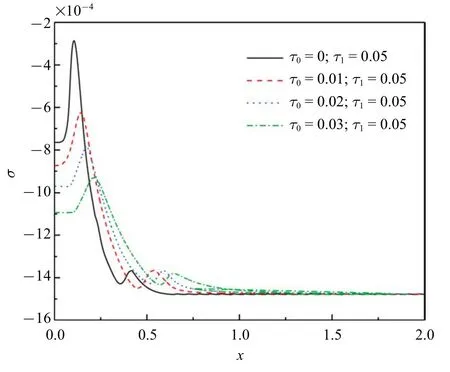
图5 无量纲应力(ν=3)Fig.5 The non-dimensional stress

图6 和图7 显示无量纲位移的分布规律.从图中可以看出,同一热源速度下,位移峰值绝对值随着τ0的增大而减小,而同一迟滞因子下,位移峰值绝对值会随着热源速度的增大而降低.还可以看到,杆的两端位移仍然为零,这是由于杆的两端固定.每一位移分布曲线满足如下规律:从零开始缓慢增大达到峰值然后逐渐降低趋近于零.

图8 和图9 显示热压电杆中无量纲电势分别在v=2 和v=3 的分布规律.压电材料有其特有的性质,即压电效应.由于热膨胀及杆端固定,杆内产生压电效应,导致在杆中产生电势.可以看出,同样的热源速度下,电势的峰值随着τ0的增大而减小.相同的迟滞因子,不同移动热源速度下,电势峰值所在的位置会不同,峰值会随着移动速度的增大而减小.每一电势分布曲线遵循以下规律:从零开始缓慢增大到峰值而后持续降低趋近于零.