超弹性材料本构关系的最新研究进展1)

彭向峰 李录贤

(西安交通大学航天航空学院,机械结构强度与振动国家重点实验室,陕西省先进飞行器服役环境与控制重点实验室,西安 710049)

引言

工程实际中常见的聚合物、橡胶、凝胶等高弹体以及诸如动脉、肌肉、皮肤等生物物质[1],具有高弹性、抗震性、耐磨性等许多优良的性能[2].纤维增强超弹性复合材料更是因为具有热解温度高、耐老化等特点,被广泛应用于固体火箭发动机绝热包覆层中[3-4].这些材料,一般都具有随机取向的分子链网络结构,由于分子间相互作用力弱、分子链间交联点稀疏等特点[5],能够经历很大变形,且在加载循环结束后没有能量耗散,被称为是超弹性材料.

不同领域研究者对超弹性材料的关注角度不同.数学家关注应变能函数的存在性、客观性及对称性等基本特性; 材料学家关注如何运用模型预测和描述实验现象; 应用领域的科技工作者关注的则是通过描述特定实验数据,对超弹性材料器件的复杂响应进行数值模拟[6].可以看出,建立超弹性材料的本构关系是所有领域研究者普遍关注的核心问题[7].

断裂分析是材料本构关系应用的典型问题,复杂变形模式和大变形构成的近裂尖区完整形貌决定了材料的断裂行为.线弹性断裂力学虽简洁完美,但由于线弹性理论在描述较大变形方面的局限,严格意义上不适用于裂尖场分析.超弹性材料本构模型弥补了线弹性模型在这方面的缺陷,是研究裂尖大变形行为的理想选择.然而,由于非线性问题的复杂性和多样性,人们对超弹性材料本构特性的认识尚不够全面,降低了人们通过断裂分析对裂尖形貌的掌握精度,难以准确指导实际的工程设计.

本文主要从体积变化、变形模式、变形程度3个不同角度,对超弹性材料本构关系研究的最新进展进行总结和分析,并对实际超弹性材料完全本构关系建立和可压超弹性材料应变能函数构造等方面的研究工作提出建议.

1 超弹性材料本构关系研究的基本理论

超弹性材料是一类具有大变形能力的非线性弹性材料,其本构特性完全取决于它的应变能函数[1,8],因而,超弹性材料性能的研究就是运用恰当的理论和方法确定该材料的应变能函数W.

根据连续介质理论,超弹性材料的应变能函数必须遵守“确定性、局部作用性及标架无关性”3 个基本原则[9].此外,作为规范化条件,应变能函数及在可压情形下表示的应力在未变形的参考构型中还应为零(本文研究以假定无初始应力和应变为前提)[7].另外,在小变形情形下超弹性理论与线弹性理论的自洽性也是一个必须遵守的条件.

为使线弹性材料应变能函数具有正定性,应变能函数需满足C(classical)条件[10],即线弹性材料的剪切模量G和体积模量K均为正,或剪切模量G为正、泊松比的取值范围为-1 ＜ν ＜0.5.类似地,超弹性材料应变能函数也需满足一些附加约束条件,但由于其非线性,这些约束条件表现为多种不同形式,例如:C 条件、B-E (Baker-Ericksen)条件、E (empirical)条件、C-N (Coleman-Noll) 条件、O-F (ordered-force)条件[9]、P-C(pressure compression)条件[11]、Drucker稳定性准则[12]等.需要指出的是,在特殊变形模式下某些条件是等同的,例如等体积变形时P-C 条件与B-E 条件等同[13];在某些材料的某些变形范围,某些条件甚至不妥,例如,E 条件对于生物聚合物是一种过度约束,B-E 条件在中等到大应变时则是不正确的[9].多个领域的研究人员都研究了应变能函数应满足的条件,但遗憾地发现,除确定性、局部作用性及标架无关性3 个基本原则以及规范化等基本条件外,其他对超弹性材料应变能函数的附加约束条件都不是基本的,其合理性仍值得商榷[7,14].

根据超弹性材料应变能函数的3 个基本原则,应变能函数应表示为变形张量不变量I1、I2和I3=J2的函数W=W1(I1,I2,J),例如Rivlin 类[15],或表示为3 个主轴方向的主伸缩比λ1,λ2和λ3的函数W=W2(λ1,λ2,λ3),例如Ogden 类[16].

未变形时3 个不变量的值为I1=3,I2=3 和J=1,3 个主伸长比的值为λ1=λ2=λ3=1,这样,参考构型中无应变能的规范化条件可表示为

可压材料参考构型中无应力的规范化条件可表示为[17]

用不变量表示即为

超弹性材料的拉伸模量、剪切模量、体积模量及泊松比等材料参数代表了变形过程中的材料特性.

在单轴拉伸变形模式下,超弹性材料的拉伸模量和泊松比可分别定义(除了本文采用的切线方式定义模量外,非线性材料还可采用割线方式定义模量)为E(λ1)=dT1/dλ1和ν(λ1)=-dλ2/dλ1,其中以应变能函数表示的单轴应力为[18]

并且,另外两个方向的主应力为零,即

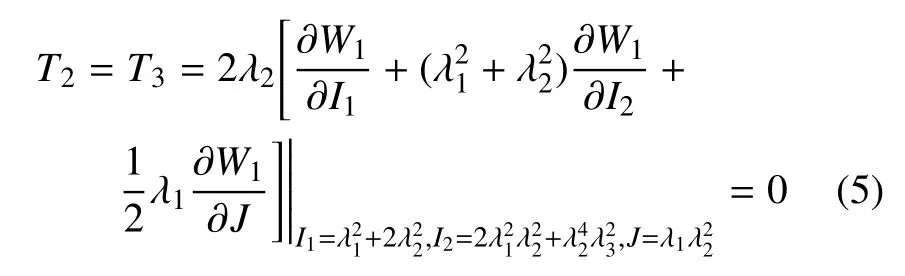
在简单剪切变形模式下,剪切模量可定义为G(γ)=dT12/dγ,其中应变能函数表示的剪应力为

在纯体积变形模式下,体积模量可定义为K(J)=dTm/dJ,其中以应变能函数表示的静水应力为

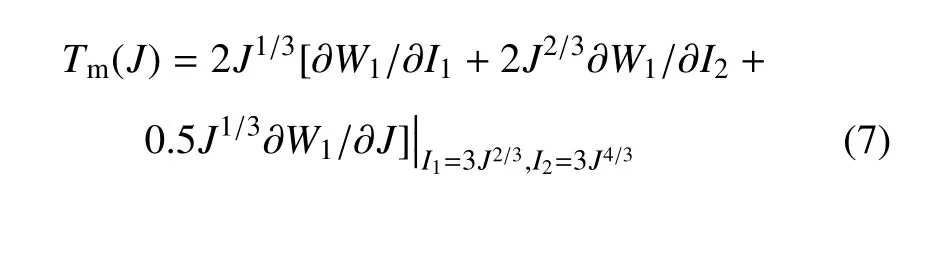
应变能函数在微小变形时需与线弹性理论自洽[13],其含义为微小变形时超弹性材料具有与Hooke线弹性材料相同的物理性质[17],一般表现为如下两个特性:一个是微小剪切量γ 时的剪切模量G(0)与线弹性材料剪切模量 ¯G具有相同的性质; 另一个微小纯体积变形时的体积模量K(1)与线弹性材料体积模量¯K具有相同的性质.事实上,由于各向同性线弹性材料只具有两个独立的材料参数,以单轴应力作用下微小变形时的拉伸模量替代静水应力作用下纯体积变形时的体积模量,将在表述具体模型自洽性条件时更为简捷,也可利用更易于实现的简单拉伸实验测试数据.

由于非线性问题的复杂性及多样性,这些材料参数常常表现出与线弹性参数迥异的性态.例如,剪切模量不能仅通过单轴拉伸实验通过拉伸模量和泊松比来得到,需通过剪切实验测量[13];在描述体积变形时,体积模量与泊松比不再完全等效,而是前者更为恰当[11].采用Hencky 应变时泊松比为常数0.5,才反映不可压超弹性材料的体积变化特征[13]; 大多材料小变形时的泊松比值在0 与0.5 之间[19],但大变形时软木塞在轴向压缩时的表观泊松比却为少见的负值[20]; 某些木材径向伸长、横向收缩时的表观泊松比甚至达到0.6～0.8[21],超出了线弹性理论泊松比值最大为0.5 的上限.最近,Sanborn 和Song[22]实验研究发现,在压缩变形模式下,硅泡沫材料的泊松比从普通的可压值转变为近不可压值,但准静态和动态时又略有不同.

研究超弹性材料应变能函数形式的方法主要有两种[23]:第一种是根据研究者自己的假设,运用基本理论,确定函数的具体形式,例如选取Rivlin 展开式[15]中的前几项,这是一种“先确定后识别” 的方法;另一种是以实验数据为依据,根据不同变形模式和/或不同变形范围时实验曲线的变化特征,选取相应函数形式,例如Rivlin 和Saunders[24]及Treloar[25]的工作,这是一种“边确定边识别”的方法.

具体超弹性材料的应变能函数模型分为数学模型和物理模型两类:运用连续介质理论,结合超弹性材料的基本条件,推演得到含模型常数的数学模型,再将其应用于材料试验测试结果,对模型常数加以识别,最终建立超弹性材料的本构关系[16,26].根据超弹性材料的分子链结构特征,运用统计力学方法,得到含微观结构常数的物理模型.以不变量表示应变能函数时,两种模型对简单情形得到的形式相同[5],但参数的意义不同:例如neo-Hookean 型超弹性材料,其数学模型的应变能函数为W1=μ(I1-3)/2,模型常数μ 在物理上可解释为微小变形时的剪切模量G(0)[16];物理模型的应变能函数为W1=nkθ(I1-3)/2,除Boltzmann 常数k和绝对温度θ 外,唯一的材料参数n具有分子链密度[5]的物理含义.数学模型可根据实验测试数据进行调整,以反映非线性的多样性;物理模型则可对变形机制给予物理解释,例如应变能函数中I1的高阶项反映了网络伸长行为的非高斯分布特性[27-28].由于与微观分子结构建立了物理关联,物理模型常常含有较少的材料常数,例如三链模型[29]、四链模型[30]、八链模型[31]和全网模型[32-33]均只含有两个材料参数.特别地,基于微观结构统计方法的物理模型为描述更复杂变形模式和更大变形范围给予了启发和指导[5].研究表明[6],结合数学模型和物理模型,运用协同多尺度方法,可建立更符合具体超弹性材料的本构模型.

总之,由于非线性超弹性材料性能及其表征的复杂性和多样性,建立本构模型时需要考虑6 方面因素[23].

(1)基本理论:本构模型必须符合理论所要求的3 个基本原则及规范化要求.

(2)附加约束:本构模型及其参数需要满足某些附加约束条件.

(3)变形模式:由于本构参数与变形模式有关,根据一种实验数据确定的本构参数,只适用于该类变形模式或被理论证明的等效变形模式,因而,本构模型还需适用于多种变形模式[9].

(4)变形范围:由于不同变形阶段的物理机理不同、变形规律差异较大,本构模型必须适用于理论上允许的整个变形范围,换句话说,只适用于小变形和中等变形的模型,不适合被用来进行变形很大的裂尖场分析.

(5) 函数形式相对简单,参数尽可能少:为便于实际应用,本构模型应选用含有较少参数的函数形式,在小变形时保持与线弹性模型自洽,尽管从实验数据角度这种较简单模型的预测效果并不是最佳[34];实际上,具有更多参数的复杂模型,有时反而造成对实验数据的过度拟合[35].

(6)参数具有明确的物理意义:若采用物理模型,其中的常数本身就具有物理意义; 若采用数学模型,其中的常数应通过规范化条件等赋予其物理意义.这是力学方式区别于数学方式研究本构模型的一个显著特征.

2 研究现状

2.1 不可压与可压本构关系研究

2.1.1 不可压本构关系研究现状

实验表明,大多超弹性材料具有体积变化非常小的特征[26],加之不可压条件极大简化了超弹性材料性能的理论研究及工程应用,因而,对不可压型超弹性材料应变能函数的研究是一项基本而重要的工作.

物理上,材料不可压时的形状改变由构型熵变化弓起[5],此时体积比J=1,只有不变量I1和I2是最基本的.目前已提出许多不可压型应变能函数,文献[23]的附录中列出了其中的29 种.

总体而言,不可压超弹性材料应变能函数的研究有3 个突破性工作.

第一个突破是基于Mooney[36]和Rivlin[14]早期工作建立的Mooney-Rivlin 类模型,是一类数学模型,其形式为[37]

式中,Cij是模型常数.

这类模型以第一变形张量不变量I1和第二变形张量不变量I2的级数形式表示,是基于连续介质理论、运用张量代数表示的超弹性非线性理论,可较好描述小变形和中等程度大变形的超弹性本构关系,是迄今描述各向同性超弹性材料本构关系较为常用的模型[38].这类工作还包括Yeoh 模型[39]、Gent-Thomas模型[40]以及Carroll 模型[26]等.最近,Liu 等[41]在neo-Hookean 模型基础上提出了一种四参数胶原纤维卷曲本构模型,由于考虑了卷曲度和胶原纤维分散系数的影响,可更好表征角膜前中央基质以及其他生物软组织的超弹性力学性能.

第二个突破是Ogden 类模型,也是一类数学模型,其形式为[16]

式中,μp与αp是模型常数.

这类模型采用Valanis-Landel 假设[42],以主伸缩比λi表示应变能函数,首次在理论上实现了对多个变形模式、较大应变范围实验曲线的准确预测,被认为是非线性弹性建模方面的重要进展[6].

第三个突破是运用基于分子网络结构的细观统计力学途径获得的应变能函数,是一类物理模型,其形式以不变量或主伸缩比表示.例如Gent 模型[43]及由此而发展的Gent-Gent 模型[44],其形式分别为

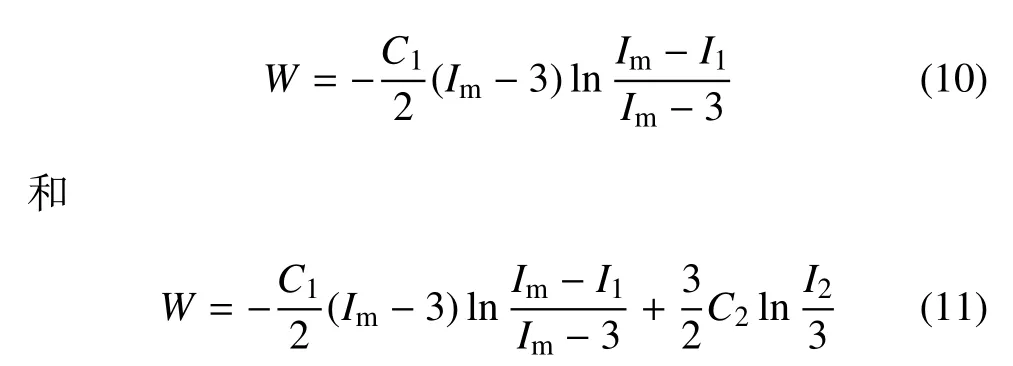
式中,C1和C2为普通模型常数,Im是分子链结构极限伸长参数.

可以看出,物理模型都具有参数少的优点,但也可含有缺乏物理意义的模型常数,反映了物理模型的另一方面重要应用.

2.1.2 可压本构关系研究现状

诸如橡胶等超弹性材料,虽然一般认为不可压,但实际上只是近不可压的,准确的本构模型需要考虑其体积可压性;在受约束条件下,即使很小的体积变化,对材料的响应都将产生重要影响[5];在多孔固体的大变形过程中,常常伴随明显的体积变化,本构模型必须具有描述体积改变的能力.另外,运用有限元方法模拟超弹性材料复杂变形时,可压材料模型更加自然,可避免不可压模型对不可压约束的额外处理[45-46]; 常见的线弹性材料都具有明显的体积变化特征(线弹性材料的泊松比一般在0.3 左右),只有可压超弹性材料模型才能成为小变形线弹性模型在大变形方面的自然延伸.这些都表明,计及体积变化的可压超弹性材料本构关系,理论上才更完善、工程应用中也才更准确.

物理上,超弹性材料的体积改变由内能变化所弓起[5].但为了利用已有不可压本构关系的研究成果,可压超弹性材料应变能函数一般通过解除不可压约束J=1 予以建立[5],据此,可压模型可分为两类.

第一类模型是将不可压应变能函数理解为与体积变形无关的等积(偏量) 应变能,再添加仅与体积比J有关的体积(静水)应变能部分[23],其形式为

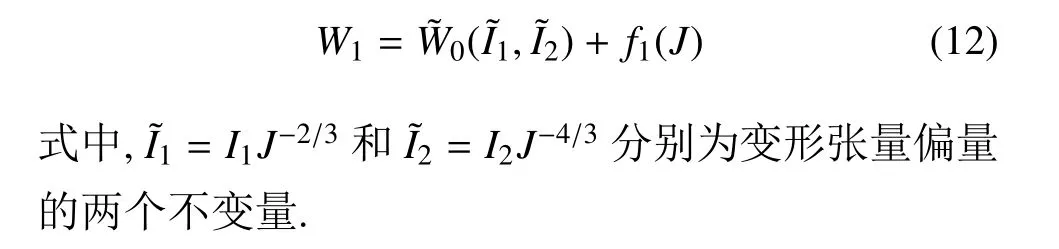
第二类模型是将不可压应变能函数理解为体积比J→1 时的极限应变能部分,再添加仅与体积比J有关的应变能部分,其形式为

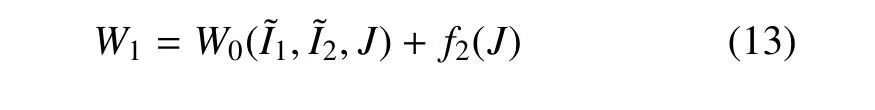
对于静水压力状态,式(12) 描述的体积变化特征为

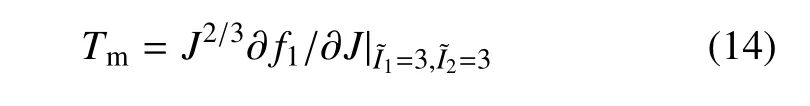
式(13)描述的体积变化特征则为

式(15) 表明,式(13) 第二类可压模型的两部分都与体积变形有关;另外,通过体积模量与剪切模量的比值变大,该模型可很好模拟材料的近不可压特性[5].

第一类可压模型的典型代表是Flory 模型[47]和可压Mooney-Rivlin 模型,其应变能函数分别为

Kumar 和Rao[48]依据式(8) 的一般Mooney-Rivlin 模型进行了可压本构关系研究,分析了项数对材料本构关系的影响,发现项数增多使得应力应变曲线的拐点增多,C01值的大小影响应力应变曲线的非线性程度.

Blatz 和Ko[49]根据唯象连续介质理论提出的模型是第二类可压模型的典型代表,其应变能函数可表示为

式中,f∈[0,1]在模型中是一个比例参数,β=ν/(1-2ν)是与泊松比有关的材料常数.

式(18)的Blatz-Ko 模型已广泛用于模拟多孔材料等可压各向同性非线性固体,在微小变形时可退化为如下的Gent-Thomas 模型[40,50]

St Venant-Kirchhoff模型[1]可归为式(13) 取f2(J)=0 的特殊情形,因而也具有描述材料可压行为的能力; 进一步研究表明[51],因I2项系数为负值而不满足多凸性附加条件,该模型在一定变形范围时将产生体积比J为负的非物理结果.

可压模型的建立需要对体积变形的实验测试,然而,这方面只有早前的少量报道.例如,Penn[52]及Fong 和Penn[53]采用膨胀仪测试了单轴拉伸过程中的体积改变,虽只得到了相对较小变形时的数据,但观察到了体积改变增大率随伸缩比增大而减小的规律.Adams 和Gibson[54]与Bridgman[55]分别开展了天然树胶的静水压缩实验,将试件置于带有活塞的圆柱型流体槽中,通过移动活塞压缩流体,改变试件所受压力.实验结果表明,对于相对较大的体积变化(例如J=0.8),材料的压力随体积变化呈高度非线性,为体积应变能函数形式的构造提供了依据.

式(12)第一类可压型应变能函数的加和分解在运用有限元方法进行变形分析时具有优势,但这种分解只是一种假设,并不是变形(或变形梯度) 张量极分解的必然结果,无小体积变化约束时会造成试件“拉伸时变厚、压缩时变薄”等非物理的大变形行为[45].Ogden[56]曾建议在第一类可压模型中再弓入等积和体积两部分耦合的第三部分应变能,然而,耦合项的存在丧失了本构关系中应力张量和弹性张量可分离的优势,更增加了确定耦合项参数的困难.

2.2 全变形范围本构关系研究

超弹性材料的随机取向分子链网络结构,使其具有承受较大变形的能力,例如Treloar 对硫化橡胶的单轴拉伸实验,轴向伸长比λ 达到了7.6[25].但是,不是所有本构模型,都能够很好地描述从小变形到中等变形、再到较大变形的完整变形过程.如图1 所示,对于氯丁二烯橡胶的大变形,基于交联聚合物链统计热力学得到的neo-Hookean 模型只适用于初始线性范围的橡胶类材料[57],三阶Ogden 模型比简单的neo-Hookean 模型则更加适合[58].

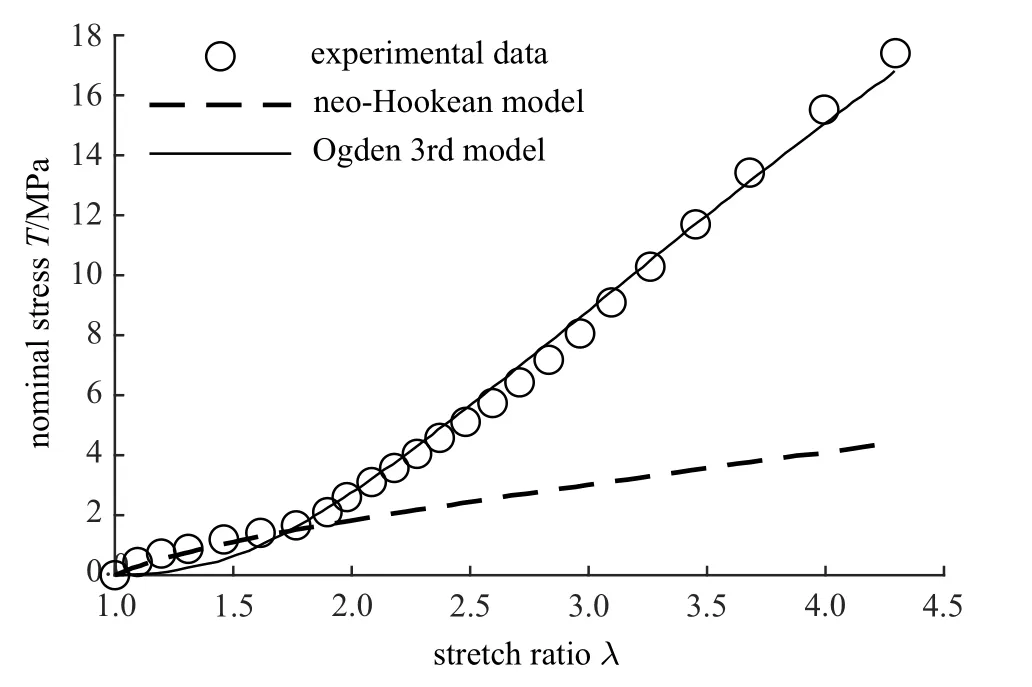
图1 neo-Hookean 模型和三阶Ogden 模型对氯丁二烯橡胶大变形的适用性[58]Fig.1 Applicability of neo-Hookean model and Ogden 3rd model for Chloroprene rubber[58]

Destrade 等[7]的定量工作表明,对于小到中等变形阶段,应变能函数W必须是两个不变量I1和I2的函数,排除了Yeoh 模型等W=W(I1)型广义neo-Hookean 类模型用于中等变形阶段的可能; Mooney-Rivlin[37]、Gent-Thomas[40]和Carroll[26]三种不同模型由于都含有两个不变量,它们对这两个变形阶段(例如1 ≤λ ＜4)都能进行很好预测,如图2 所示.鉴于得到了不依赖应变能函数具体形式的结论,该工作被认为是超弹性材料本构关系研究方面的一项重要工作.

图2 W=W(I1,I2)型应变能函数对不同变形阶段的预测效果[7]Fig.2 Predictions of strain energy functions described by W=W(I1,I2)for different deformation regions[7]

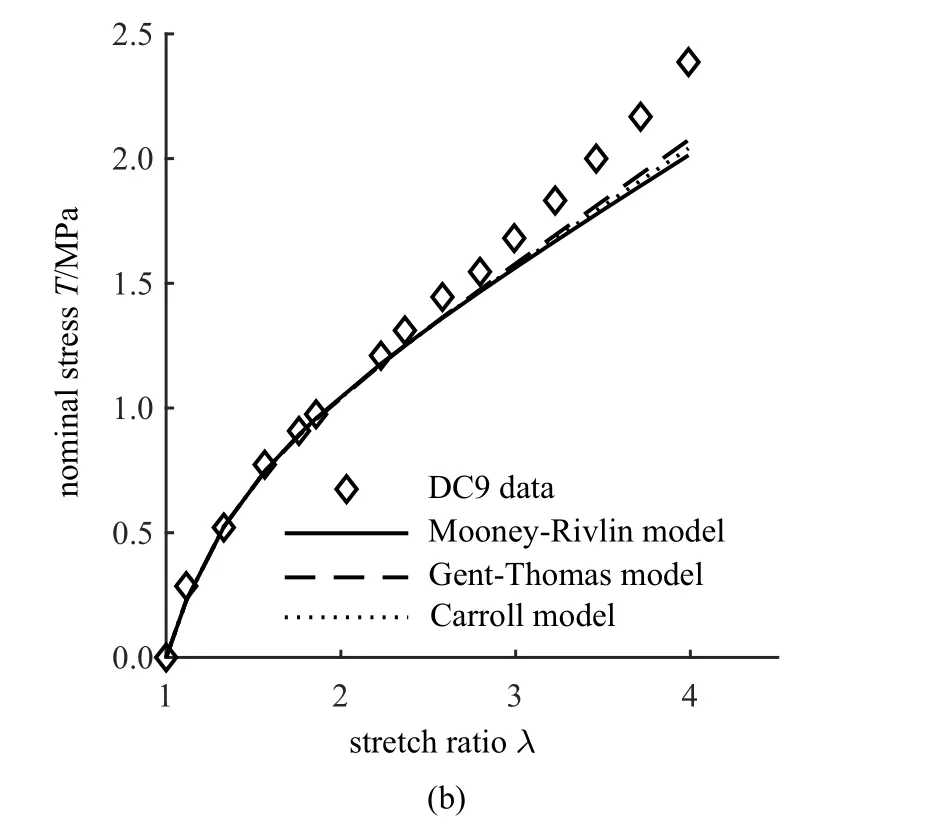
图2 W=W(I1,I2)型应变能函数对不同变形阶段的预测效果[7](续)Fig.2 Predictions of strain energy functions described by W=W(I1,I2)for different deformation regions[7](continued)

建立能描述全变形范围拉伸实验的本构模型,需要与实际实验曲线相结合的建模步骤.Destrade等[7]还对实验数据进行了Mooney 图变换g(z)–z,即横轴运用伸缩比的倒数z=1/λ、纵轴运用折算应力g(z).这样,如图3 所示,整个拉伸曲线被划分为变形机制不同的3 个阶段:第一阶段是小到中等变形阶段,此时聚合物链容易展开,Mooney 图几乎为直线.第二阶段是应变硬化阶段,此时成束链团的展开使得材料的刚度增加,表现为Mooney 图中曲线的“向上翻转”.第三阶段是分子链的极限伸长阶段,随着分子链拉伸至其极限,材料出现了剧烈的刚化现象.三个阶段的特征分别通过不同的函数形式在应变能函数中予以反映,最终得到的应变能函数为

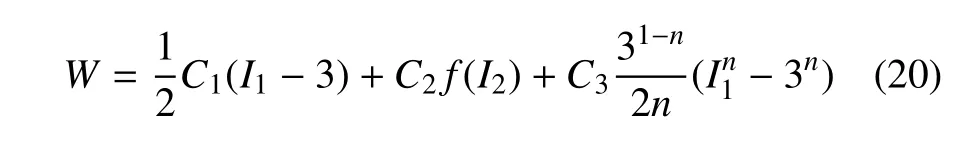
式中,C1,C2,C3与n均为模型常数.

式(20) 对实验数据的全变形范围能很好拟合,在统计力学框架内还可给出物理解释,是数学模型与物理模型相结合开展超弹性材料全变形范围非线性本构关系研究的典型案例.对Treloar[25]经典实验数据及Dobrynin 和Carrillo[59]数据的分析结果表明,Pucci 和Saccomandi[44]提出的三参数Gent-Gent 模型能表征橡胶类非线性弹性材料完整变形过程,五参数Carillo-Dobryin 模型也是一种很好的选择,并通过预测简单剪切实验对这两个模型的强健性进行了验证.

图3 典型拉伸实验数据的Mooney 图变换[7]Fig.3 Mooney plots of typical uniaxial tension’s data[7]

同样基于Treloar 的单轴拉伸数据,Beda[23]通过对整个变形过程进行分级和渐进式增加高阶项的做法,提出逐步分析法,研究全变形范围的不可压超弹性材料的应变能函数.由于只有实验数据与前一步模型预测的偏差在增加项预测时起作用,因此新增加项不影响在前一步已很好预测的变形阶段,从而转化成非线性优化问题并加以求解,得到的应变能函数为

式中,C,K,α 和β 为模型常数.

式(21) 推广了Hart-Smith 模型[60],并再次证实了第二不变量I2在应变能函数中的关键作用.

依据小变形到中等变形、再到大变形的全变形范围的单轴拉伸实验,学者们开展了卓有成效的研究工作,得到了式(20) 和式(21) 等全新形式的本构模型,它们更符合具体材料的实验曲线特征.

2.3 多种变形模式本构关系研究

单轴拉伸的实验测试和理论研究固然非常基本和重要,但实际问题的变形场往往是复杂多样的,多种不同的变形模式同时存在,因而,本构关系的研究还应考虑对单轴拉伸以外其他多种变形模式的适用性.不可压各向同性材料一般具有3 对共6 种均匀变形模式,即单轴拉伸与等双轴压缩、单轴压缩与等双轴拉伸以及纯剪切与面内压缩[9].因此,每对中各取其一的单轴拉伸、单轴压缩及纯剪切3 种变形模式被称为基本变形模式.在材料试验中,最常见的变形模式为单轴或双轴拉伸[34],较少见的是简单剪切或纯剪切以及扭转[61],更少见的则是复合剪-拉或复合扭-拉[62],能包含3 种基本变形模式的完整的材料实验并不多见.

研究应变能函数对多种变形模式的适用性,考察不同变形模式时模型常数的差异,是超弹性材料本构关系研究的一项重要工作.Ogden[16]研究表明,neo-Hookean 模型仅能描述橡胶在小到中等程度的剪切变形,但增加了I2的Mooney–Rivlin 模型其适应性可明显改善,对橡胶特性的预测与实验数据更吻合[6].虽尚不能从理论上解释neo-Hookean 模型和Mooney-Rivlin 模型产生差异的原因,但实例分析表明[24,63],为了适应更多不同的变形模式,应变能函数都需包含第二不变量I2.

Carroll[26]详细分析了3 组典型的实验数据,即Treloar[25]给出的简单拉伸、纯剪切、复合剪-拉以及等双轴拉伸的数据,Rivlin 和Saunders[24]给出的简单拉伸、纯剪切以及复合剪-拉数据及一个主变量不变而其他主变量变化等多种实验数据,以及Jones和Treloar[64]给出的面内一个主伸长不变、另一个变化的实验数据.基于其共有的“曲线形状不变性”[42],他提出了建立本构模型的3 步骤方法:第一步用neo-Hookean 模型进行模拟,识别参数,使neo-Hookean 模型在一定变形范围内(例如1 ＜λ ＜4.5)对Treloar 的拉伸数据能够准确模拟; 第二步建立变形范围修正模型,计算neo-Hookean 模型对更大变形范围Treloar拉伸实验数据预测的应力残差,藉此提出变形范围修正模型并识别其参数; 第三步建立模式修正模型,计算前两步所得模型对Treloar 等双轴拉伸这一不同变形模式实验预测的应力残差,藉此提出模式修正模型并识别其参数.最终,通过3 步分别得到的应变能函数的加和,得到可适用于多种变形模式的应变能函数为

式中,A,B和C为模型常数.该模型对实际多种变形模式的预测效果如图4 所示.

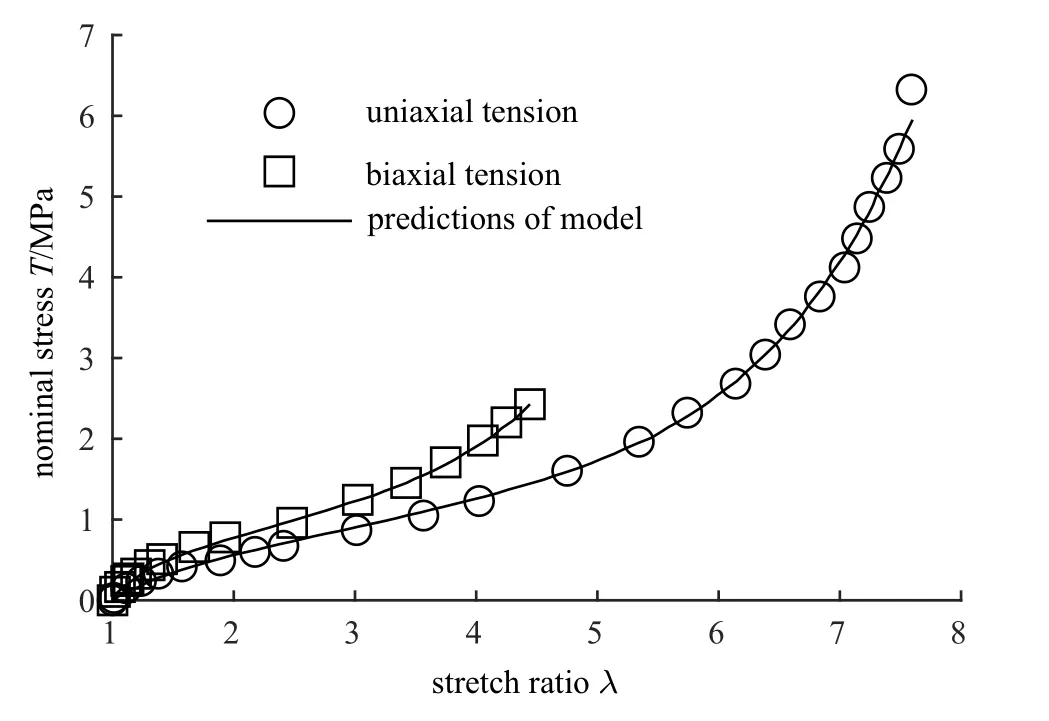
图4 式(22)对Treloar 的单轴拉伸和等双轴拉伸两种模式实验结果的预测效果[26]Fig.4 The predictions of Eq.(22)for Treloar’s uniaxial tension and biaxial tension[26]

利用Gent[43]弓入的分子链结构极限伸长参数Im,并通过新增项,Carroll[65]新近对Treloar 等双轴拉伸全变形范围的实验数据进行了很好拟合,得到了可同时适用于拉伸和等双轴拉伸模式的全变形范围的应变能函数为

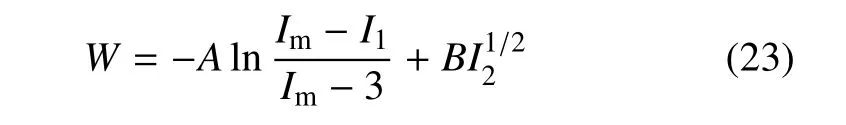
式(22) 和式(23) 在函数形式上非常接近,这一有趣现象表明,从宏观实验数据角度,采用式(21)的数学模型和式(22) 的物理模型,都可获得适合多变形模式的超弹性材料本构关系.

3 研究展望

实际上,从物理学观点,超弹性材料本构关系必须是普遍的,虽不苛求其能够描述所有超弹性材料的力学行为,但要求其能够描述某种具体材料多种变形模式下全变形范围的非线性力学特性,因而,对不同变形模式及不同变形范围的适用性是超弹性材料本构关系研究的重要课题,同时也是本构关系在断裂分析等超弹性材料实际应用中迫切需要解决的根本问题[7].

3.1 完全本构关系研究

依据等双轴拉伸实验数据,Carroll[26,65]研究了其全变形范围的本构关系,与单轴拉伸相比,变形模式中涵盖了等双轴拉伸,虽然还只是一种等效的单向压缩模式; 同时研究了单轴拉伸、纯剪切及复合剪-拉3 种多种变形模式,但变形范围又相对较小(λ ＜4).因而,仍需开展超弹性材料的建模方法研究,以建立适用于多种变形模式、能描述全变形范围的超弹性材料的完全本构关系.

3.1.1 多变形模式本构关系

研究发现,应变能函数的具体形式对其描述能力及有限元数值实现将产生重要影响[7].对于非线性材料,根据一种变形模式所建立的本构模型对其他变形模式可能效果很差、甚至不适用[9].

笔者认为,以小到中等变形范围(例如单轴拉伸时1 ≤λ ≤3)的实验数据为对象,可通过“赋初始模型-增加修正项-多模式验证”的研究步骤,开展多变形模式本构关系研究:第一步赋初始模型,即以某模型(例如neo-Hookean 模型或Mooney-Rivlin 模型)为初始模型,以单轴拉伸(基本变形模式) 实验数据进行参数识别;第二步增加修正项,即针对另一典型(例如等双轴拉伸或剪切)变形模式,根据初始模型的预测差异,结合相关数学模型或相应变形机制的物理模型,确定修正项函数,进行参数识别;第三步进行多模式验证,即将模型用于其他变形模式,验证对更多变形模式的适用性,确认模型的强健性.

多变形模式本构关系,适用于小到中等变形范围的超弹性材料的复杂响应分析,但对裂尖区变形很大的断裂问题分析仍不适用.

3.1.2 完全本构关系

超弹性材料的单轴拉伸实验曲线一般都有一个明显的大变形阶段,例如Treloar 单轴拉伸实验的伸长比λ 达7.6,对应工程应变超600%,因而,全变形范围本构模型不仅具有理论研究意义,而且具有实际应用价值.

将多模式本构关系延伸至全变形范围,可建立超弹性材料的完全本构关系:以较大变形程度(例如单轴拉伸时λ ＞3) 的拉伸实验为依据,以多变形模式本构关系为初始模型,运用“赋初始模型-增加修正项-多模式验证”的研究步骤,构造应变能函数,建立超弹性材料的完全本构关系.

理论上,完全本构关系完整描述了超弹性材料的非线性特性,可应用于所有情形的力学响应分析,包括实际结构的复杂应力场问题和裂纹尖端的大变形场问题.

3.2 不可压与可压本构关系的相关性研究

由于不可压材料的实验数据最为丰富,3.1 节展望了不可压完全本构关系的研究.实际的超弹性材料一般只是近不可压的,可压超弹性材料本构模型在理论上更一般,在微小体积变形时还可退化为不可压模型,因而,研究可压超弹性材料的完全本构关系在力学理论和工程应用上都具有重要意义.

对于超弹性材料,首先研究较简单的不可压型本构关系,再经扩充发展成为可压型本构关系,符合人类的认知过程;从科学研究的角度,从更一般的可压型本构关系出发,通过不可压条件进行退化,可揭示材料不可压特性的物理机制.事实上,一种简单的不可压模型会通过性能差异很大的多个不同的复杂可压模型退化而来,单从不可压模型难以追溯得到材料自身独特的可压或近不可压特性.所以,不可压与可压本构关系的相关性问题是一个严肃的科学问题.

以硫化橡胶材料为例,Fong 和Penn[53]进行了单轴拉伸实验研究,同时获得了拉伸应力与伸长比的关系曲线和体积比与伸长比的关系曲线.他们运用两项不可压Mooney-Rivlin 模型,取应变能函数为

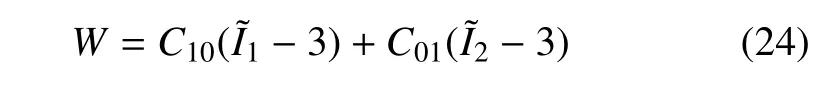
通过对拉伸应力与伸长比关系曲线拟合,得到模型常数为C10=0.181 MPa 和C01=0.082 MPa.

根据与线弹性理论的自洽性,由式(24) 得到该材料的初始剪切模量为=2(C10+C01)=0.526 MPa.

若依式(12) 建立形如式(17) 的第一类可压Mooney-Rivlin 模型,通过对拉伸应力与伸长比关系曲线和体积比与伸长比关系曲线同时进行拟合,Horgan 和Murphy[46]得到式(17)中的模型常数为C10=0.092 MPa,C01=0.237 MPa 和d=1000.1 MPa.

根据与线弹性理论的自洽性,由式(17) 得到该材料的初始剪切模量为=2(C10+C01)=0.658 MPa,初始体积模量=2d=2000.2 MPa,进而得到初始泊松比ν=0.4998.与式(24)不可压模型相比,初始剪切模量相差25.1%.

若依式(13) 建立第二类可压Mooney-Rivlin 模型,其应变能函数取为

通过对拉伸应力与伸长比关系曲线和体积比与伸长比关系曲线同时进行拟合,在相关系数R2=0.998 6时,可得到式(25)中的模型常数为C10=0.307 MPa,C01=-0.157 MPa 和d=1605.4 MPa.

根据与线弹性理论的自洽性,由式(25) 得到该材料的初始剪切模量为=2(C10+C01)=0.300 MPa,初始体积模量=2d-8(C10+C01)/3=1605 MPa,进而得到初始泊松比ν=0.499 9.与式(24)不可压模型相比,初始剪切模量相差达43.0%.

上述两种可压模型,虽然都得到了接近于0.5 的近不可压初始泊松比,但由于C10和C01两个与不可压特性密切相关的模型常数值差异较大、甚至发生了正负号变更,可以说不能退化为相应的不可压Mooney-Rivlin 模型,特别是,关键的初始剪切模量相差悬殊.

为此,在建立可压超弹性模型时,应当根据不可压模型已得到的模型常数,进一步构造体积变化影响项.

本小节的初步分析表明,对于超弹性材料,从不可压本构到可压本构的延拓,仍有一些值得研究的新问题.

4 结论

近一百年、特别是第二次世界大战结束之后的七十余年来,对超弹性材料的性能研究已经取得了丰硕成果,在科学研究和工程应用的多个方面得到了应用.然而,模型的多样性及差异性从侧面折射出人们对目前状况的不满足及该问题研究的开放性.

超弹性材料性能理论研究和实际应用的最基础问题是真实而完整的本构关系研究,虽已提出超30种(类)模型,但仍有很大的发展空间.本文对超弹性材料本构关系的基本理论、发展史上的重要进展及目前的最新成果进行了梳理,分析了超弹性材料完全本构关系研究的理论价值和工程意义,对超弹性材料性能的进一步研究及其他非线性材料性能的研究也大有裨益.