借“可视化”思维工具,呈“有意义”学习经历
——例谈数学手账在“回望课”中的运用
2020-11-03□许艳
□许 艳
所谓“回望课”,顾名思义,就是指回头望一望,“望”教学的学习情况,“望”教学的学习效果,“望”教学部分知识的得失,等等。教师可充分发挥“数学手账”这一可视化思维工具的特点,将其有效地运用到“回望课”中,这不仅是对知识的分享,更是一种生成性资源的运用。
一、系统梳理,追溯知识源头
精心提炼数学手账中的知识梳理板块,做到从点上切入,线上突破,面上整合,能引领学生理清知识的脉络,构建完整的认知结构。这是上好回望课的前提。
(一)忆——回忆知识点
回望课中,教师可引导学生“望”课题,回忆所学的知识,“望”学生自己做的数学手账,回忆每个板块的重要知识点。
例如复习“比例”这一单元知识时,有位学生的数学手账里呈现了鱼骨图(如图1),教师可运用鱼骨图引领学生回忆“比例”单元的知识点:比例的意义、比例的基本性质、比例的应用等。每根鱼骨的分叉点表示知识点的形成,这里需要让学生充分讨论,借助具体情境激活学生头脑中的知识链,查漏补缺,建立知识框架。
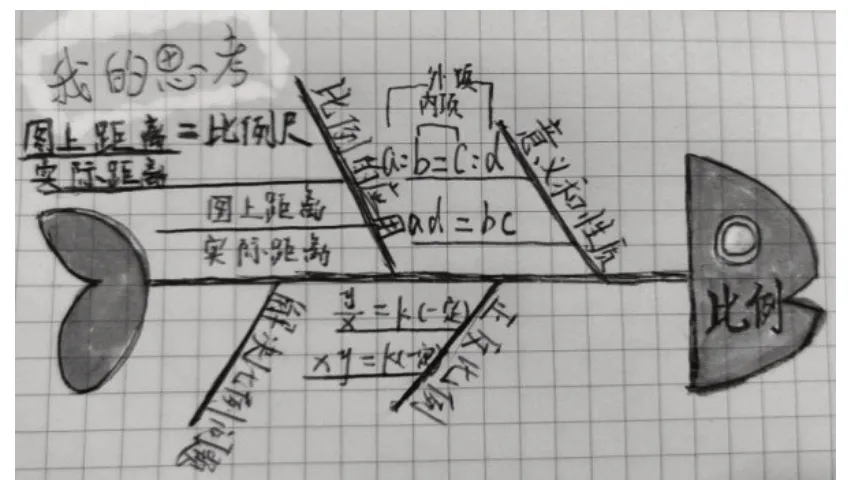
图1
(二)清——厘清知识线
回望课中教师不仅需要引导学生把握所学的知识点,还应该重视梳理、沟通知识的过程,将所学知识前后贯通,以帮助学生厘清知识线,分清解题思路,弄清各种解题方法。
例如在复习“百分数(二)”这一单元时,教师借助学生的手账(如图2),先呈现这一板块的知识要点,即“折扣、成数、税率、利率”,而贯穿这些知识点的主线就是百分数的意义。通过这一主线,帮助学生理解生活中百分数的不同呈现方式。首先,让学生口头复述各概念的含义;其次,在此基础上呈现内容摘要,并通过举例来支撑对概念的理解,还需要举一反三,巩固基本概念;最后,通过相应的基础练习,提炼出解题关键。这一清晰的记录,让学生对百分数这一板块的重点知识一目了然,深入理解。

图2
(三)建——构建知识面
整理归纳知识体系、构建知识网络是回望课中非常重要的环节。构建知识网络,组块化呈现知识内容,可以有效降低学生的记忆负担。
例如“圆柱与圆锥”这一单元的知识点比较多。在回望课中,教师要有意识地组织学生把散乱的知识串成链、结成网,找出图形之间的联系并加以对比,把碎片化的知识串珠成链,构成层次鲜明、结构清晰的知识网。部分学生将“思维导图”运用到数学手账的记录中(如图3),构建的知识网由浅入深、由表及里。
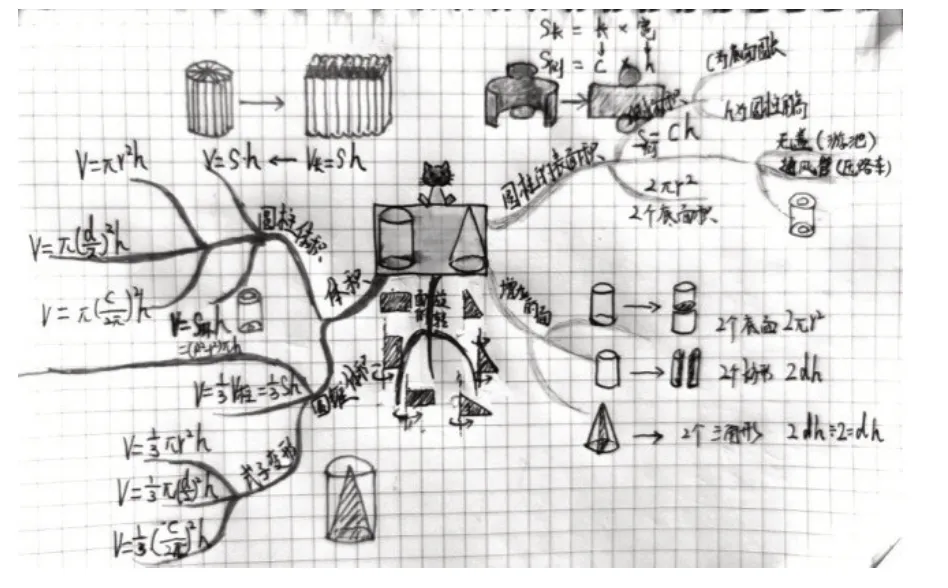
图3
课堂上教师有效利用这一资源,首先从“面的旋转形成体”入手,引导学生熟悉圆柱与圆锥的特征;接着从“体中寻找面”深入,理解圆柱表面积计算的难点——侧面积,借助圆柱展开图加深对侧面积与长方形关系的认识;然后帮助学生回顾圆柱体积计算公式的推导过程,运用转化思想,思考圆柱与长方体、等底等高圆柱圆锥的关系,巩固圆锥体积计算公式;最后拓展到圆柱、圆锥横截面的计算。该思维导图中的每个主干都是知识要点,每个分支厘清了知识的来龙去脉,展示了公式的灵活运用。如此整理复习,能够使知识之间的相似处和差异点变得清晰直观,也能够使学生的思维走向高阶。
二、问题引领,叩问核心素养
在问题的驱使下,引导和帮助学生用所学的数学知识去发现问题和解决问题,将知识结构转化为认知结构,是上好回望课的核心。
(一)觅——解核心之问
“学起于思,思源于疑。”学生数学手账里提出的质疑,可以作为宝贵的复习资源加以合理利用,师生共同探讨解决。在数学手账里学生提出的问题往往是随机产生的,势必良莠不齐,有些过于细小和琐碎,有些与教学目标无关。这就要求教师课前做好“觅疑”的准备。
1.从知识的“产生点”上寻问题。如教师在“圆柱与圆锥”单元数学手账中发现了学生的共性问题(如图4)。

图4
2.从知识的“结合点”上寻问题。如教师在“比例”单元数学手账中发现了疑惑问题(如图5)。
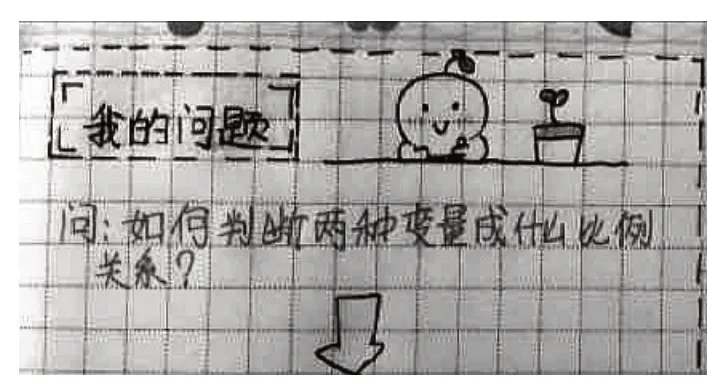
图5
回望课上,教师将共性的问题、有价值的问题展现出来,通过辨析、释疑来解决学生的核心之问。
(二)辨——破疑难之问
在辨疑的过程中,教师组织学生围绕疑问,由浅入深,由表及里,层层思辨,螺旋式地理解核心概念。
如围绕学生提出的共性问题“为什么同样一张长方形的纸,绕长或宽旋转,得到圆柱体积不一样”,教师组织学生展开探究分析。首先,通过直观操作,学生观察到以长为轴旋转而成的圆柱瘦瘦高高的,以宽为轴旋转而成的圆柱矮矮胖胖的。其次,教师引导学生猜想运用怎样的旋转方式得到的圆柱体积大,并请学生说说理由。通过假设验证,得出结论。最后,将探究方法迁移到核心问题“沿着不同的直角边旋转后,形成圆锥的体积大小相同吗”。
这样通过猜想、操作、验证等探究过程,破解学生的疑难杂症,从而提高学生思维、分析、判断的能力。
(三)释——固能力之问
辩疑讨论、突破难点是复习的重要环节,但还没达到最终目的。教师应结合学生的疑问和讨论结果加以归纳总结,并出示题目组织学生进行练习,以达到巩固所学知识的目的。
如有学生在“比例”单元数学手账中提出:“如何判断两种变量成什么关系?”通过辩疑,学生得出判断正比例、反比例的方法,此时教师需要趁热打铁将概念内化,不断巩固,以提升学生解决问题的能力。
觅疑、辩疑、释疑是一种学习过程,更是一种探究过程,有助于学生主动对问题进行分析和探究,促使其学习能力提升。
三、实践运用,走向数学理解
数学手账的运用不仅是对知识的梳理,也是对难点的深入思考,更是让学生运用学到的知识去发现生活中的数学问题,解决生活中的问题,以真实情境下的数据为背景创编相关的数学问题。这是上好回望课的关键。
(一)享——让数学理解更直观
“回望课”的最后一环节,请数学手账实践运用的当事人表达、分享自己的观点,让其他学生进行点评、补充、完善,从而更直观地理解这一板块数学知识的运用,在分享交流过程中扩大信息量,发现生活中的数学问题。如进行负数的复习时,学生在实践板块中将疫情数据完美融入数学学习(如图6)。
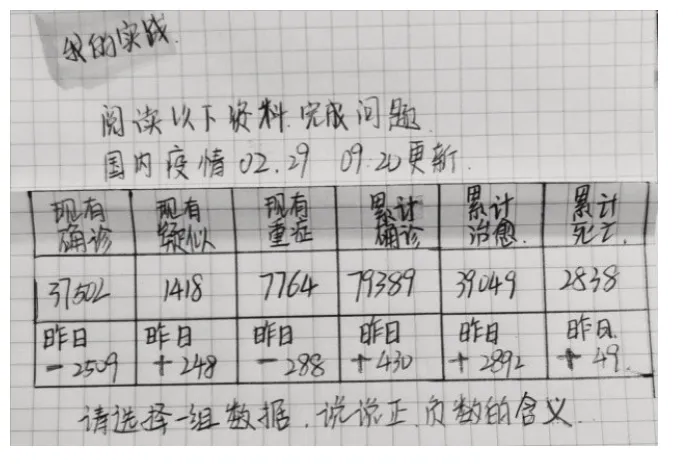
图6
(二)思——让数学理解更深度
实践运用是学生对所学知识再思考、再审视的过程,因此,在分享的同时,教师要善于创设反思的机会,抓住反思的契机,引导学生与数学“深度”对话。
如复习“用正比例解决问题”时,教师组织学生分享这一实践成果(如图7)。除根据基本数量关系列比例外,学生还想到可以根据不同的数量关系列不同的比例。另外,根据以往解决问题的经验,学生发现这些比例没有具体的数量关系,觉得这样的比例没有意义。此时,有学生提出反驳意见:两个呈正比例的量一定存在“相对应两个数的比相等(一定)”的规律,所以,无论式子的形式怎样,只要是相对应的两个数的比相等,这样的比例式都存在“正比例”的意义。教师相机在矛盾冲突中加以引导,借助该学生数学手账里的实践运用,通过“深度”对话,让学生对用正比例解决问题进行了再认识、再提升。

图7
(三)用——让数学理解更透彻
数学手账中实践运用板块的展示,能让更多的学生提高数学应用意识。例如学完比例的应用后,有学生通过实际测量,运用比例尺的相关知识进行计算,求得图上距离后将自家的平面图完美地画下来(如图8)。通过展示与解读比例尺的运用,学生明白了学习比例尺的价值,将数学知识应用于生活实际中。

图8
总之,将数学手账这种思维表征工具应用于“回望课”,既可以丰富教学方式,改进教学现状,又能够促进学生高效巩固知识、深度思考,发展其创造性思维。
