数学本真教学
——“读思达”的影响及作用*
2020-11-03唐少雄
□唐少雄
福建师范大学余文森教授倡导的“读思达教学法”,从阅读、思考和表达三个层面对课堂教学提出新观点、新理念。余教授指出:“教学过程就是学生的学习过程,学习过程即阅读、思考、表达的过程,阅读、思考、表达是教学的三个基本环节。学生只有经过这三个环节的相对完整的学习,才能把知识转化、内化为素养,所以这是一种以学生学习为本位的让核心素养落地的教学法。”“读思达”是基本的教学方法,为数学本真教学(以下简称本真教学)的探索提供了理论支撑。
一、影响:“读思达”对本真教学理论的发展
“读思达”教学法是核心素养背景下,对“立德树人”育人导向的践行,对课程改革具有重要意义。
(一)发展本真教学理论
本真教学基于学情,关注数学教学的育人价值和实践应用,注重培养学生学会阅读,学会思考,清晰表达数量关系和数学模型。“读思达”教学法倡导让学生经历完整的学习过程。个人阅读、提出问题和学科表达,对“本真教学”具有较强的理论引领,丰富了本真数学的内涵:突出数学阅读的地位和作用,准确把握学生的知识经验,引导学生经历知识发生发展的过程;凸显思考,遵循学生的思维规律和认知特点,让学生学会有逻辑地思考,创造性地思考;自主表达,学会个性表达数学理解和探究发现,引导学生用自己的语言表达数学规律和思维过程。“读思达”教学法丰富了本真教学的理论内涵,把数学学科核心素养的培育落实在课堂教学中。
(二)形成数学本真教学模式
阅读、思考、表达是素养本位教学法,是其他教学法研究的信号源和方向标。本真教学从教材、课堂和学生三个层面践行“读思达”,突出三个“重”:一是重教材阅读,引导学生自主阅读,读懂教材,读明思路,读透思想;二是重课堂思考,课堂教学启发学生独立思考,养成良好的思考习惯;三是重学生表达,启发学生用自己的思维探究数学,用自己的思考理解数学,用自己的语言表达数学。在读、思、达三个阶段中,形成本真教学模式(见下图)。
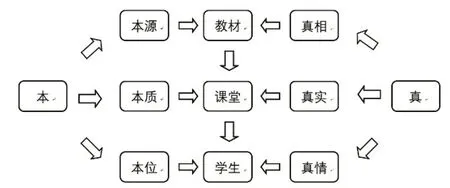
(三)指导本真教学课堂实践
针对数学教学中弱化学生的数学阅读和数学表达的现象,本真教学要突出阅读与表达。数学阅读包括读懂知识、读宽知识、读透知识三个层次。读懂知识,即要鼓励学生课前预习,读懂所学的知识内容,读懂所介绍的方法和路径,读懂数学探究的过程,读懂数学表达的呈现方式,等等。读宽知识,即要多渠道收集相关知识,阅读相关课外书籍,网络查询相关内容,多方获取知识,体验获取知识方法的多元性。读透知识,即读出知识间的联系,理解数学与生活的联系,把握知识的研究方向,等等。数学表达的方式可以是语言表达、图像表达、算式表达、操作表达、实验表达等。教师要鼓励学生结合自己的理解,学会多样的表达方式,力求从数学角度理解知识,把握关系,呈现个性的表达方式。
二、导向:“读思达”对本真教学方法的引领
本真教学在“读思达”教学法理论引领下展开,读是学习之本,思是教学之真,达是本真之宿。
(一)读是教学之本
阅读的本质是信息的吸收。数学阅读的弱化导致学生的信息输入不足,直接影响学生对教学内容的接受和理解。因此,本真教学强调数学阅读,注重培养学生多渠道获取知识的能力,主要有课前预习、课中自学和课后研学。课前预习侧重阅读书本知识,课中自学重点读懂获取知识的方法指导,课后研学是拓宽数学阅读。通过数学阅读,让学生主动提出问题、主动探究知识本源,把握知识生长点、知识连接点、知识结构点,从本源上理解数学。
(二)思是教学之真
本真教学追求理性思维,培养学生学会思考。思是教学之真,教学的根本任务不仅是记忆、理解和掌握知识,而且要培养学生的思考力、判断力和鉴赏力。因此,培养和训练学生的数学思维是教学的主要任务,要注重引导学生在阅读理解的基础上,经历真实的探究过程,要关注学生的思考过程和认知过程,培养学生创造性思维的发展。本真教学中,思考应贯穿于教学的全过程,是教学的出发点,也是教学的落脚点。
(三)达是本真之宿
数学表达是本真教学的归宿。本真教学关注核心素养的育人目标,确立了学习的根本任务是学会阅读、学会思考、学会表达。学习过程中学生的主动阅读、主动探究,其最终回归点就是数学表达,数学表达是学生阅读理解的一种真实展现。数学表达包括语言表达、算式表达、符号表达、图像表达、关系表达等,通过表达,学生达到能力的升华。数学表达是本真教学的根本任务和价值导向,要让学生学会在阅读理解的基础上表达自己的观点和看法。
三、作用:“读思达”对本真教学实践的指导
“读思达”倡导读、思、达三者有机融合,相互促进,其中读是基础,思是关键,达是核心,三位一体。
(一)增进“读”与“思”的融会
数学阅读应伴随思考,阅读的过程也是思考、反思和推理的过程,是读与思的融合。本真教学倡导课前阅读、课中自学、课后研学。课前阅读带着导学问题,课中自学带着明确要求,课后研学带着数学问题,主动探究、主动学习。
以人教版四年级下册“三角形内角和”一课为例,课前预习导思:什么是三角形的内角和?不同类型的三角形内角和相等吗?三角形内角和有什么规律?你想怎么研究三角形内角和?除了了解课本上介绍的方法外,你还知道其他方法吗?让学生带着问题阅读,让数学阅读有思考。课中自学导思:教材中的“画几个不同类型的三角形。量一量,算一算,三角形3个内角的和各是多少度”你怎么理解?“我的这个直角三角形的内角和大约是180°”“我的是锐角三角形,也是……”让你想到什么?是不是所有的三角形内角和都是180°?你想怎么验证?课本介绍的这种方法是否可以验证任何三角形?再次阅读课本,思考会更加深刻,探究会更加有效,使得数学学习更具合理性和实效性。课后研学激思:三角形内角和的探究方法有什么值得借鉴的?四边形的内角和是多少?五边形、六边形、N边形呢?这些图形的内角和有怎样的规律等等,引导学生继续探究计算多边形内角和方法间的联系(见下图)。

(二)促进“思”与“达”的贯通
本真教学着眼学生需要,立足课堂真实,探究数学真相,还原数学本来的呈现方式,显现学生真实的思考过程和真实的数学表达。学生可以借助图像、符号、算式及语言表达他们的探究过程,以及他们对知识的理解,实现思与达的贯通,让学习真正发生。
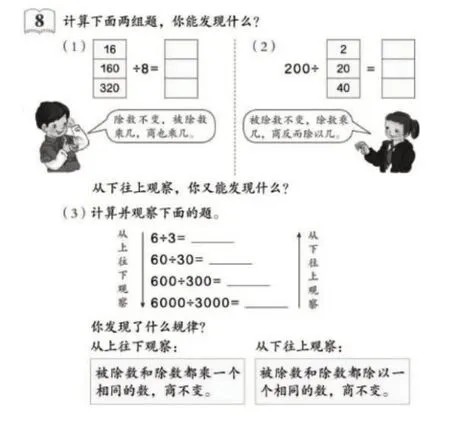
以“商的变化规律”为例(见下图),可以引导学生回忆“积的变化规律”,促发学生思考:商的变化规律可能是什么?引导学生提出猜想:猜想一,除数不变,被除数扩大(缩小)几倍,商也扩大(缩小)几倍;猜想二,被除数不变,除数扩大(缩小)几倍,商也扩大(缩小)几倍。数学需要有理有据的思考,有了猜想,还要有验证,有推理,它们是更深层次的思考。猜想一借助举例,可以尝试让学生自主发现规律,学生也可以借助“积的变化规律”进行语言表达。猜想二是教学的难点,用举例验证的方法也可以发现规律:被除数不变,除数扩大(缩小)几倍,商反而缩小(扩大)几倍。反思猜想与发现之间的不同,可以进一步启发学生思考:为什么除数的扩大(缩小)几倍,商反而缩小(扩大)几倍?可以让学生借助除法意义的理解,尝试自主表达:在除法里,除数表示分的份数,除数扩大(缩小)意味着分的份数多(少)了,当然每一份就少(多)了。在两个活动经验的基础上,启发学生进一步思考:被除数和除数怎样变化,商才能不变?学生结合思维活动经验,提出猜想三:被除数和除数同时乘以或除以一个不为0的数,商不变。从猜想一、猜想二到猜想三的提出和验证,让学生在猜想中暴露思维,在验证中完善表达。在探究中,学生运用猜想、验证、观察、比较、推理等思维方式,实现了真正意义上的数学建构。
(三)推进“读思达”的深化
本真教学吸取“读思达”理论的精髓,加强学生的数学阅读,激发数学思考,学会数学表达,培养全面发展的人。
以人教版教材“平行四边形的认识”为例,由于学生对平行四边形的了解经验先于认识,思维定式影响他们对平行四边形特征的理解。如何引导学生认识平行四边形?教师可以从本源上寻找学习切入点,先让学生寻找生活中的平行四边形物体,并尝试把平行四边形画出来。这里的“画”出来,就是抽象,画的过程是经验和思维的激活,也就是表达图形的特征。当然,停留这一层面的教学仍然是浅层次的认知,需要进一步的数学思考和语言表达:平行四边形有什么特征呢?怎么验证你的发现?引导学生进入探究环节,借助测量工具,如直尺、三角尺等进行实践测量、验证,经历从感性到理性,从片面到全面,从现象到本质的探究过程。在表达层面,需要培养学生有依据的数学表达,如经过测量发现平行四边形对边分别相等,经过平移发现平行四边形对边分别平行……进一步培养学生数学表达的条理性和准确性,最后理解平行四边形的定义“两组对边分别平行的四边形,叫作平行四边形”。
本真数学教学需要在“读思达”理论引领下不断丰富和发展,本着务实求真的科学态度探究本真数学课堂教学模式,推进基础教育课程的改革。
