基于ANSYS的汽轮发电机定子绕组端部模态分析

张 乐，苗 虹，何启源，杜 轩，蔡天伍

（1.四川大学 电气工程学院，成都 610065；2.东方电气集团 东方电机有限公司，四川 德阳 618000；3.重庆理工大学 机械工程学院，重庆 400054）

汽轮发电机运行时的端部振动问题是影响机组能否安全稳定运行的主要原因。研究表明：当定子绕组端部径向电磁力的频率与定子自振频率接近时，就会产生共振［1-2］，进而机组会由于振动偏大引起线圈绝缘磨损、线棒疲劳断裂及发电机漏水等问题。为有效降低发电机运行时的振动幅值，解决机组在运行过程中由于结构共振或绑扎带松动引起的振动偏大的问题，必须对汽轮发电机进行端部模态分析及试验研究。

国内外学者也从试验和理论分析两方面对定子绕组端部的振动特性做了研究，刘石等［2］利用解析法建立定子绕组端部的简化模型，得到绕组端部产生共振的原因，提出了引起发电机端部共振的2条重点论据；张青雷等［3］主要研究了定子端部结构的建模方法，以及温度对端部模态参数的影响，有限元分析中主要通过梁单元、壳单元对其有限元模型进行离散；陈伟梁等［4］利用定子绕组的循环对称特性，研究了定子结构对其模态参数的影响；杨昔科等［5］只采用有限元分析法，对150 MW 级汽轮发电机定子绕组端部进行模态分析，忽略了绑扎带预紧力对定子端部模态的影响，计算结果准确与否并未通过试验进行验证；陈力飞等［6-7］采用有限元法与模态试验相结合的方式对发电机定子绕组端部固有频率做了详细的分析，定量分析了端部结构材料差异对于其模态参数的影响；Drubel O等［8］运用有限元数值模拟方法对汽轮发电机定子端部的动态特性进行了分析，模型构件简化较多，有限元模型中采用三维实体单元模拟线棒，用弹簧单元模拟绑带，用壳单元模拟其他构件。综上所述，目前的研究主要集中于发电机端部简化模型模态的计算。国内外均未见到考虑端部所有主要构件，通过研究不同结构部件的建模方法及各部件之间的融合方式来建立高精度有限元等效模型，以及对发电机端部进行参数化研究的报道。但是，对于发电机定子整体结构而言，零部件模型的准确建立和融合关系的准确模拟会直接影响有限元分析结果的准确性［9］。

在汽轮发电机设计阶段通过有限元软件较为准确地计算其模态参数，能使其定子端部的自振频率在制造前就可避开共振区间。综上所述，本文以某型汽轮发电机为研究对象，综合利用了实体单元、梁单元建立了有限元等效模型，完成了定子端部的有限元模态分析，得到其模态振型及自振频率。并对该定子进行了锤击法试验，将试验结果与计算结果进行对比分析，验证了有限元模型和计算方法的可靠性，为定子绕组端部模态参数的数值模拟提供了可靠的依据。

1 模态分析的有限元数学模型

模态分析实质上是通过坐标变换把原物理坐标系统中的对应向量转换到模态坐标系统中来描述。其中坐标变换的变换矩阵为振型矩阵，其每列为各阶振型［10］。发电机结构离散后的拉格朗日运动方程为

式中：［M］为质量矩阵；［C］为阻尼矩阵；［K］为刚度矩阵；｛u｝为节点的位移矢量；为节点的速度矢量；为节点的加速度矢量；F为作用在结构上的外载荷形成的结构节点动载荷向量。

定子端部模态分析属于自由振动问题，即F＝0，在实际的工程实践中，阻尼对结构固有频率及振型的影响不大，所以在进行分析时可以忽略阻尼的影响，如此就可得到无阻尼自由振动运动方程：

假设结构的自由振动为简谐振动，u（t）＝A cosω，式中A为节点振幅向量，ω为自由振动频率，把该式代入式（2）可以得到齐次方程：

因此可以得到结构的自振频率方程为

由式（4）能够求出结构的n个自振频率。令λ＝ω2，则式（3）可以化为广义特征方程：

将得到的自振频率代入特征方程（5）中可得到特征值矢量，将特征值矢量进行归一化处理后可以得到结构的主振型［11］。

发电机端部绕组的固有频率与其结构的刚度和质量密切相关，为了避免发电机在运行过程中绕组由于受到二倍工频电磁力的作用产生结构共振问题，必须对发电机定子绕组端部进行模态分析。

2 定子绕组端部模态的有限元分析

2.1 定子绕组端部有限元建模

汽轮发电机定子绕组端部结构复杂，主要构件包括定子绕组、绑扎带、锥环、支撑块等。其中定子绕组是定子端部结构中最为复杂的构件，建模也最为困难。其一是由于其截面结构复杂，在端部整体结构中需进行合理简化，本文结合线棒的实际受力情况，在等效线棒和实际线棒具有相同动力特性的前提下，采用实心等效线棒代替实际线棒。其二是由于上下层线棒的排列方向不一致且相互交错，建模时需将其展开，使其渐开线的形状形成一个圆锥面上的空间曲线，在平面极坐标下，圆的渐开线展开方程式为

式中：ρ是渐开线上任意一点p（x，y）到原点的距离；r是基圆的半径；θ为该点与X轴的夹角；t是参数。在建模软件中打开绘制草图界面，根据线棒物理模型及渐开线参数，绘制出端部线棒曲线，以此曲线为轨迹，端部截面为扫描截面，扫描可得线棒三维模型。而后按照位置关系，装配时采用每根绕组自上而下的方式，得到发电机定子绕组的三维模型，如图1所示。

从定子端部模态分析的文献来看，就位于线棒渐开线部分用于加固2层线棒及固定层间构件的绑扎带而言，由于其结构复杂，建模时往往被简化掉，仅采用相应的接触代替。这样虽然建模更简单，计算分析更加容易，但分析结果不够准确。本文在建模时，根据该型机组定子绕组端部的实际情况，使实心等效线棒之间相互切割，预先形成多个节点，再将其按实际结构依次连接，以建立绑扎带的结构。其他部件保留其结构形状及特征尺寸，以保证模型和实际结构具有较高的一致性。最终将各部件导入装配图中，并按总体设计，将各零部件装配起来，装配完成后励端模型如图2所示，汽端模型如图3所示。

2.2 定子绕组端部模态计算

为使计算更易收敛且计算量更低，在整体质量及结构刚强度不受较大影响的前提下，对模型进行有限元计算时做了一定的简化。定子绕组端部模型用有限元单元进行离散时，对定子端部模型进行了一定的切割。除绑扎带的其余结构部件均采用线性的六面体实体单元进行离散，结合绑扎带的实际受力情况，绑扎带采用只拉不压的梁单元进行离散。

发电机定子绕组端部是由多种材料构成的，进行有限元分析时，需根据其物理模型等效各部件的材料性能参数。定子端部金属构件的相关力学性能参数可通过手册获得，其他材料主要通过相关力学试验获得其性能参数，主要构件材料的密度、弹性模量、泊松比如表1所示。

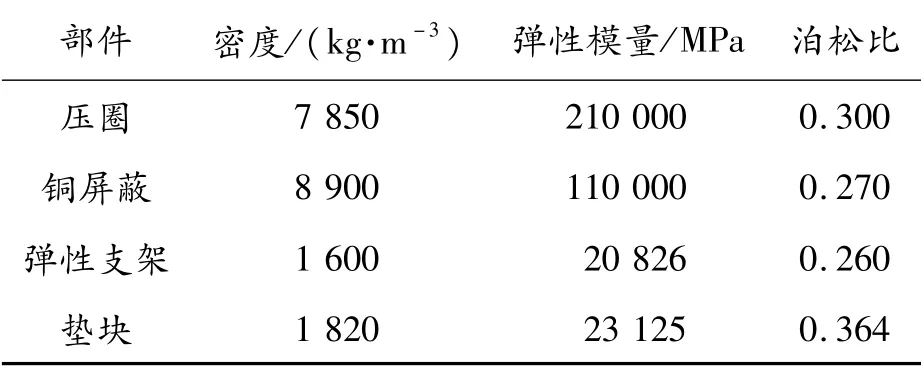
表1 定子端部主要构件力学性能参数

定子绕组端部各部件状态的准确模拟对其整体结构刚强度有较大的影响，从而影响有限元计算结果的准确性。本文在计算时重点考虑定子绕组端部各部件的接触情况以及绑扎带预紧力对模态参数的影响。陈力飞等［6］将绑扎带和垫块之间的边界条件设置为刚性固定，而忽略了绑扎带预紧力对定子端部模态的影响。定子绕组端部线棒间的绑扎带能够更好地将上、下层线棒固定在一起，同时绑扎带也将整个定子绕组端部近似连接为一个整体，线棒间绑扎带的连接能够大幅度地提高整个端部的刚度。为检验绑扎带预紧力对定子绕组端部各阶模态振型对应固有频率的影响，本文运用有限元法分析了当绑扎带处于不同预紧力时，定子绕组汽端各阶模态振型所对应固有频率的变化，绑扎带预紧力对其各阶固有频率影响结果如图4所示。

由图4可以得出：当绑扎带预紧力从0.5F0增加至F0时，各阶振型对应的固有频率都有所提升。其中椭圆（四节点）振型的固有频率值增加了2%左右，八节点振型的固有频率值增加3%左右，变化最为明显。但是，当预紧力从F0增加到1.25F0时，各阶固有频率变化很小。分析结果表明：绑扎带预紧力大小能够明显地影响各阶振型对应的固有频率。因此，对于绑扎结构的定子绕组端部，在分析其固有频率时需考虑绑扎带预紧力对固有频率的影响。本文在进行端部模态分析时，结合定子端部装配时的实际情况，将绑扎带预紧力大小设置为F0。

经过多次试算分析，发电机定子的接触及计算边界条件设置主要包括：支架和绑环之间、环形引线和绝缘支架、环形引线和层间垫块之间的连接关系。其中，最为关键的是线棒与垫块之间的约束方式，结合线棒的实际受力情况，上、下层线棒之间安放有间隔垫块，然后用绑扎带将线棒捆绑在一起，因此间隔垫块与绑扎带之间设置为相应的约束关系。

通过有限元软件ANSYS的计算分析，得到了该型汽轮发电机定子绕组端部的各阶振型及固有频率。励端椭圆振型固有频率为57.66 Hz，汽端椭圆振型固有频率为61.74 Hz，励端各阶振型如图5～7所示，汽端各阶振型如图8～10所示。

3 定子端部模态试验

3.1 模态试验方案

为了验证上述发电机定子端部有限元分析方法的可靠性，对该型发电机定子绕组端部进行了锤击法模态试验。

本次试验采用CRAS模态测试分析系统，试验主要包括3个环节：激励环节、响应环节、数据采集分析环节，测试系统连接如图11所示。

试验采用“多点激励单点响应”的方法，激励部分是通过力锤快速地敲击绕组端部，给端部绕组施加脉冲力。结合本次试验激励所需的能量及频带范围，力锤锤头采用频带较窄的橡胶锤头，锤头上有测量激励信号的力传感器；响应信号则是由安装在线棒上的加速度传感器接收；模态分析软件控制数据采集箱采集并存储测试的数据，最后由模态软件对测得的数据进行处理，得到被测物体的模态参数，试验系统如图12所示。

此次模态试验根据发电机的定子结构，在定子绕组汽励两端圆锥面的内表面外圈均匀布置22个测点，端部结构如图13所示，测点布置如图14所示。试验时将加速度传感器固定在4号测点，力锤依次快速敲击每个测点，每个点敲击4次取平均以降低试验误差。根据力信号的衰减情况、响应信号频谱以及相干函数水平，判断此次数据采集是否有效，根据工程设计的实际情况，本次试验只分析200 Hz以内的固有频率。

3.2 试验数据处理

数据采集完毕后，通过CRAS软件对测试数据进行处理，得到各测点的频响函数。对试验得到的频响函数进行测量方向、约束方程等综合处理，并检验其模态的正交性，最终得到发电机绕组端部的模态振型。励端椭圆振型对应的固有频率为67.02 Hz，汽端椭圆振型对应的固有频率为78.13 Hz，模态试验得到的励端各阶振型如图15～17所示，汽端各阶振型如图18～20所示。

3.3 试验结果与计算结果对比分析

通过锤击法试验和有限元计算均得到了端部的各阶固有频率及模态振型，将试验结果与计算结果对比发现：汽励两端试验和有限元计算得到的各阶固有频率误差均低于7%，满足工程设计要求，结果如表2所示。

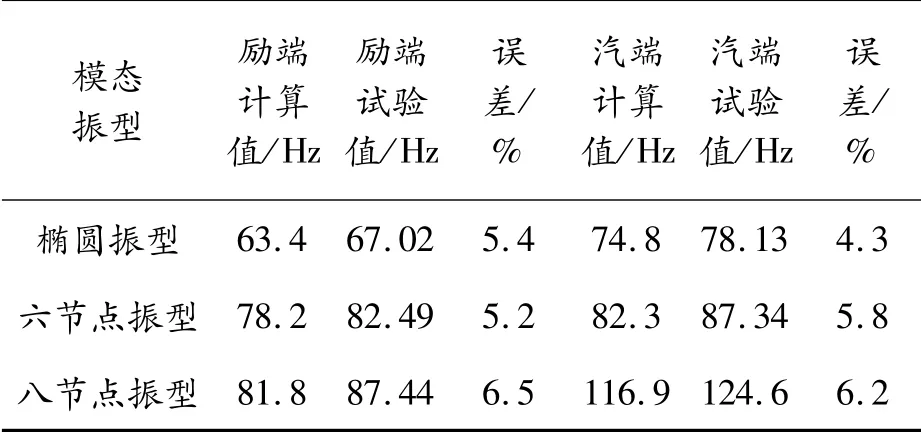
表2 计算结果与试验结果对比

4 结束语

本文以某大型汽轮发电机为研究对象，对其定子绕组端部的振动特性进行参数化分析。根据发电机物理模型建立了定子端部的精细模型，在有限元软件ANSYS中完成了定子端部的有限元模态分析，得到各阶模态振型及固有频率。对该机型定子端部进行锤击法模态试验，将试验结果和计算结果进行对比分析，汽励两端椭圆振型对应的固有频率误差分别为4.3%和5.4%，其余各阶固有频率误差均小于7%。分析结果表明：采用本文的有限元分析方法得到的计算结果较为精确，验证了有限元模型和计算方法的可靠性。

通过本文所述有限元模态分析方法，在汽轮发电机设计阶段就能较为准确地计算其模态参数，可使机组固有频率在生产制造前就避开共振区间，为今后产品的优化设计及新产品研发提供了具有工程实用价值的依据。