基于实时主方向估计的素描渲染

张严辞，龚昱宁

（1.四川大学 软件学院，成都 610207；2.四川大学视觉合成图形图像技术国家重点学科实验室，成都 610065）

随着卡通渲染类游戏的兴起，人们开始不仅仅满足于基于物理的渲染，非真实感渲染出的效果也越来越受到消费者的青睐。素描是一种运用单一色彩表现物体美感的绘制手法［1］，用素描这种绘画的方式对游戏等可交互产品进行渲染，增强了这类产品的趣味性，吸引了消费者的眼球，增加了产品商业价值。

近几年，关于非真实感渲染的研究结果层出不穷。其中文献［2］归纳了大部分基于表面的有说明表现力的可视化方式，其提到使用曲面的第二基本形式［3］或者使用高阶多项式拟合的［4-5］方式来估计素描渲染所需要的主曲率，但其需要耗时的顶点属性的预计算而无法做到实时渲染。文献［6］基于文献［7］提出了使用焦平面的主方向估计方式来估计主方向，但无法很好解决因为复杂模型顶点间属性线性插值带来的噪声问题。

在获得主方向的基础上，关于对素描风格的渲染，文献［8-9］使用了基于文献［10］思路的线卷积积分，但该方法存在透视错误的问题。文献［5］提出使用贴图进行旋转和粘贴的方式来绘制，但这种方式绘制出来的线条与主方向偏差较大且存在空间耦合性的问题。文献［11］提出了深度学习来获取一定的方向进行线卷积积分，但此方法不适用于需要高帧率的实时渲染。

针对以上问题，在实时主方向估计上，本文对构建焦平面的方式来获取主方向的算法进行了改进，相比于原方法对于复杂模型能得到更加鲁棒的结果，相比于无法改变顶点间关系的主方向预计算，有着可以应用到蒙皮网络与顶点动画的优势。其次，本文提出了一种线卷积方式，凭借有序抖动与GPU端硬件的纹理采样优势，突破了原有离散的像素点与2D空间的限制，提高了单帧的渲染效率，且有空间耦合性与投影正确性。最后，使用两个主方向的角平分线作为线卷积的方向，降低了画面整体的复杂度，并对渲染结果进行了风格化处理，使渲染效果更加接近手绘素描的效果。

在适用场景上，由于本文渲染算法为通过几何缓冲进行实时后处理，无需对模型进行预处理或对传统渲染管线更改，有较强空间耦合性，可以应用到需要实时交互且有蒙皮动画的应用上，且不会产生如文献［6］中雨幕效果的问题。因此渲染算法能在常用的消费级渲染引擎上直接使用（如Unity或Unreal Engine4），并应用到基于这些引擎的可交互产品中（如手机或桌面端游戏、影视作品、三维漫游以及可交互教学应用等），为可交互产品展现的场景带来风格化渲染效果，激发使用者的兴趣以提高产品的商业价值。

1 相关工作

1.1 离散主方向估计

曲面上一点的主方向定义为该点法曲率取得最大和最小的方向。主方向对应的两个法曲率被定义为主曲率。由于主方向可以表现物体在某一点的变化趋势，使用主方向为基础在许多风格化与可视化中得到了广泛的应用［13-14］。因此，如何求解主方向成为了一个重要的主题，近几年有许多关于如何求解主方向的研究。在微分几何上，某一点的主曲率与主方向可以由该点Weingarten映射［16］或者形状算子［3，15］进行特征值分解求得解析的解。但对于由三角网络与几何缓冲表达出离散的值而言，难以直接使用主方向的定义求解。现有算法中，对离散值进行主方向估计算法分成两类，基于模型空间的预计算以及使用屏幕空间几何缓冲进行实时估计。对于模型空间的预计算，现有3种较为常见的思路。

第1种算法是用高阶多项式［4-5］对曲面进行拟合然后得到某个顶点的主方向。

第2种算法是先对每个三角面构建切平面［15-16］，之后使用如差分的形势计算该三角面沿着一条边的法向量的变化量，然后将该方向与法向量的变化量代入形状算子的等式来求得形状算子矩阵的值，并将3个方向的结果使用最小二乘法进行回归来得到更为准确对于每个三角面的结果。对于每个顶点，首先根据顶点切平面与三角面的切平面的位置关系，将其中一个平面围绕着两个平面法线的叉乘的方向进行旋转，使得两个平面共面（若两个平面旋转前已经共面，则不用旋转）。之后求得形状算子在顶点坐标系下的值。由于一个顶点对应多个三角形，即一个顶点对应多个形状算子的值，本文使用Voronoi区域［17］值进行加权求和来得到一个更为准确的值。并将最后的结果进行特征值分解得到该顶点的主方向。这种算法，有着对于复杂度较高的模型，有着容易产生不平滑以及不连续的结果的问题［7］。

第3种算法是利用焦平面［7］，其核心思想是利用曲面上一点的法向量与其周围临近的法向量会在某两个平面上共线的这个特性，而这两条共线的线便是主方向，这2个平面便是焦平面。对于离散三角网络的估计，文献［7］使用了L-M方法进行回归以求得更准确的解，根据论文中的数据，这样一种算法比第2种提到的算法，对于普通模型产生的结果略微不够准确，但相对于复杂的模型能产生更为准确以及连续的结果。

总的来说，针对模型空间的算法虽有较高的准确性，相对于模型离散化而产生的噪声有一定的鲁棒性，但是其预计算需要大量时间，有着无法实时应用到有顶点动画与蒙皮网络渲染需求的缺陷，且会带来额外的存储空间。

对于屏幕空间的主方向估计，根据离散几何上对主方向的定义，使用与临近像素点的差分来获取曲面的高阶偏导数，并利用高阶偏导数计算每个像素点的形状算子以求得主方向的值。但这样的算法因使用了三角网络光栅化后线性插值得到的噪声严重的世界坐标和法线方向，使得结果不够准确。因此，文献［6］提出了使用焦平面来实时计算主方向。该算法与模型空间的预计算方法类似，但是没有使用回归的方式求更准确的解，只使用目标像素点以及与其临近的两个像素点来进行计算。

1.2 线卷积积分

线卷积积分作为一种让向量场可视化的图像处理技术最早由文献［10］提出，文献［18］对其进行了改进，文献［19］将该算法应用到了图像处理的运动模糊上。本文将该算法应用到实时渲染中。原算法的核心是在二维向量场上沿着每个像素点对应的向量场方向，每一步跨越一个像素点到另一个像素点，并通过新像素点对应的向量场的方向到达新的像素点。同样的方式也可以推广到三维，但三维向量场的渲染需要使用体渲染，这样的方式难以与现有管线相整合做到实时渲染。

1.3 有序抖动

有序抖动最早是一种半透明的印刷技术。在图形学中，有序抖动对于体积光等体渲染降低迈进步数［20-21］，在图像处理中，对图像降噪等有着较为重要的作用。本文将该方式用于对线卷积积分的改进，提升了线卷积积分的性能。

1.4 素描风格渲染

文献［12］提出了使用不同的光照等级对应不同纹理的方式来进行素描渲染，这种渲染算法存在线条绘制的方向固定、难以表现清物体的结构特点且透视错误的问题。文献［6］用贴图进行旋转和粘贴的方式来绘制，存在空间耦合性的问题，且由于是后处理，每个像素点UV坐标旋转围绕的点的位置必须固定，使得绘制得到的方向与实际主方向偏差大，且存在透视错误的问题。文献［8-9］使用线卷积积分的方式来进行渲染，但该算法存在透视错误的问题，且得到的结果存在叠笔不充分的问题（在素描绘制中，艺术家对于颜色较黑的色块往往使用了从几个方向进行“铺调子”的方式，叠笔绘制）。

2 本文方法

为阐明具有广泛的适用性与鲁棒性的实时主方向算法，以及基于该算法的更为接近手绘素描的渲染算法，从3个部分讲解本文使用到的算法：适用范围更广且更具鲁棒性的实时主方向估计，透视正确且高效率的线卷积积分，基于艺术导向的素描风格渲染，本文使用的算法的流程如图1所示。

2.1 适用范围更广且更具鲁棒性的实时主方向估计

基于模型空间主方向估计需要预计算，不适用于蒙皮动画与顶点动画。而基于屏幕空间的主方向估计只与每一帧绘制得到的几何缓冲有关，并且若使用延迟渲染的方式，几何缓冲很容易获得，使其很容易整合进现有管线中。

在屏幕空间的主方向估计方法中，本文对焦平面进行主方向估计的算法进行改进。相比于直接使用差分估计形状算子的方式，基于焦平面的算法有着更好的对因为光栅化带来的噪声的抵抗能力。

原主方向估计［6］算法的核心思想是：首先构建以计算的像素点的法线为z轴，该点世界坐标为原点的正交坐标系；之后选择两个临近像素点计算其法线射线在该坐标系下的表示，并求得两个法线射线与该坐标系xy平面的交点（u1x，u1y，0），（u2x，u2y，0），并求的法线方向在该坐标系下，z值为1的方向向量（n1x，n1y，1），（n2x，n2y，1），之后利用如下等式求解计算焦平面的位置。

该等式化简后为一元二次方程。若方程有解，则将得到的2个λ代入式（2）中，便可以求得主方向在该坐标系下的表示，将该向量转换为世界坐标下的表示即为所求的主方向。

经复现后，发现此方法存在一定的缺陷：

1）原算法未对如何选取两个临近像素点的法线射线与焦平面的交点中的一个进行分析，因为在大部分情况下选择其中任意一个均会得到正确的结果。但是对于如圆柱曲面以及其类似的曲面上，若选取的临近的法线射线的像素点是与目标像素点在同一个圆周上的点，则会存在该像素点的法线射线与焦平面的交点与目标像素点的法线射线与焦平面的交点重合的问题（相交于该圆周的圆心）。若计算主方向时选取了该像素点，则由于浮点数精度问题，2个交点本应重合，但进行相减不为零向量，归一化后得到的主方向与原来主方向相差过大，使得整体算法缺乏鲁棒性。

2）由于只选择了一组临近像素点（2个），并根据其计算主方向，本文经过实验，发现这样的算法对于形态较为简单的几何体（如文献［6］中展现的球体、圆柱体、茶壶）能得到较为准确的结果，但是对于较为复杂的形体，部分估计值会随着这组像素点的选取而改变。并且随着物体靠近屏幕方向，会出现一些像素点在求得焦平面解二次方程时出现判别式为负数的情况，导致使得该点的像素值无法确定，使得整体算法缺乏鲁棒性。

为了解决上述2个问题，受文献［7］中通过焦平面对模型空间中的离散三角网格的主方向使用L-M方法进行回归的启发，本文采用另一种思路进行更快的线性回归。由于使用2个临近的法线射线以及目标像素点的法线射线就可以计算出一组主方向，首先构建目标像素点所在的切平面的一个正交坐标系，接着分别求出目标像素点的周围8个像素点的世界坐标与法向量在该坐标系下的相对坐标，并分别对这个8个像素的法线射线进行计算。对于每个像素在切平面下表示的法线射线的方向向量记为（nix，niy，1），与切平面的交点记为（uix，uiy，0），其中i的不同取值代表目标像素点周围8个临近像素点中的一个的计算结果。

接下来，将上方与左方、上方与右方、下方与左方、下方与右方、左斜上与左斜下、左斜下与右斜下、左斜上与右斜上、右斜上与右斜下这8组像素点分别与目标像素点在切平面正交坐标系下的几何信息代入式（1），每一组分别求得最大主曲率或最小主曲率分别对应的应在主方向上的2个点（px1，py1，0）与（px2，py2，0）。

将得到的结果使用最小二乘法进行回归。由于主方向与切平面平行，因此不考虑z轴方向，算法的伪代码如下：

算法1 对采样结果进行回归求得更为准确的主方向

输入：

Point［17］通过以上算法求得的17个坐标

axis X，axis Y分别对应切平面坐标系下的X轴与Y轴在世界坐标系下的表达。

输出：

PrincipalDirection世界坐标系下的主方向for（int i＝0；i＜17；i++）

｛

sum_x+＝Point［i］.x；

sum_y+＝Point［i］.y；

sum_xy+＝Point［i］.x* Point［i］.y；

sum_x2+＝Point［i］.x*Point［i］.x；

count++；

｝

k＝（sum_xy-sum_x*sum_y／count）

k／＝（sum_x2-sum_x*sum_x／count）；

b＝（sum_y-sum_x*k）／count；

PrincipalDirection＝normalize（axis X+（k+b）* axis Y）

使用最小二乘法进行线性回归规避了之前提到了计算量大需要反复迭代，使用到超越函数的问题。之后像文献［22］的方法进行平滑处理。

在非生物模型占主导地位的场景或渲染影视作品的场景下，可以只选用上方、下方、左方、右方4个像素点的采样结果进行计算，原因如下：

生物模型（如人体以及各种动物）表面上相对平滑且起伏细节较多，较非生物模型更复杂，因此对生物模型较多的场景应该应使用8个像素点进行采样。而对于非生物等人造物模型占主导的场景（如家具或汽车等机械），其表面比较规则，细节较少，因此对非生物模型较多的场景应使用4个像素点进行采样。

几何缓冲是由光栅化线性插值得到的，因此噪声产生于顶点间顶点属性线性插值。若模型顶点密度较高，相当于该模型其对物体表面采样数更多，线性插值带来的噪声的影响就越小。影视作品其往往使用顶点密度较高的模型，对其应使用4个像素点进行采样并计算结果。而对顶点密度较低的实时交互类应用（如游戏等），由于其使用顶点密度较低的模型，而导致噪声问题严重，因此需要使用8个像素点采样并计算得到结果。

这样的算法能在GPU上能够以较快的速度进行处理。作为实验结果，本文发现使用这样的算法计算得到屏幕空间主方向对于复杂模型有着更为准确的结果，并且基本能回避上文提到的文献［6］中的两个问题。

为了进一步解决物体靠近带来的判别式为负数的问题，本文设置一定的深度等级作为对照。当深度低于一定指标时，在采样时选择离目标像素点一定距离外的像素点来构建法线射线。当物体离视平面较近时，临近像素点由于线性插值和浮点数误差，几个像素点的空间位置上与平面过于近似而无法得到正确的结果。而使用有一定距离外的像素点，会在一定程度上减少线性插值带来的影响，增大几个像素点在空间位置上的差距，减少其与平面的近似程度，从而得到更为正确的结果。除此之外，对于一些已经被判定为平面的点，在进行对主方向进行平滑的时候，搜索其附近的点，将其附近没被视成平面，且和该点在同一平面上的点的主方向赋给该像素点。这样的做法能在一定程度上增强算法的鲁棒性。

对于不同场景、深度等级及其对应的像素，采样间隔设置方法如下：首先找到场景中曲率最低的曲面，若有多处则对多处分别按照以下思路计算深度等级，并对相同深度区间取最高间隔作为该部分的间隔。首先将该曲面贴近裁剪平面，之后将被错误视为平面的像素点中最高深度值作为最高深度等级，并逐一提高像素采样的间隔距离，直到曲面上没有像素点被视为平面。之后降低1像素间隔，并将物体向裁剪平面中远平面偏移，直到没有曲面上的像素点被视为平面，并记录此时曲面上最低的深度值，将该深度值视为使用此时间隔的临界点。并按照如上方法降低像素采样距离并设置深度值，直到间隔变为1。

2.2 透视正确且高效率的线卷积积分

传统线卷积积分以每一个像素点为单位，视一个像素点内向量场不会发生变化。故每一次向前传播时，会固定跨越一个像素点。本文对该算法进行改进，不再将一个像素点内的向量场视为不变，而是作为一个通过插值得到的连续向量场参与后续运算。

本文算法对于非整点的采样，对其临近的4个顶点使用双线性插值获取采样值，并通过控制步长得到风格化的效果，使用有序抖动降低了迈进的步数以提高性能。这样的插值操作在GPU端由于其能被硬件实现而有着较高的效率。

文献［8］中使用到的2D线卷积积分，其直接用主方向与透视矩阵相乘的结果，作为其进2D线卷积积分的2D向量。这样的做法存在透视错误，因透视矩阵的构造，对于有相同方向向量的却在裁剪空间中不同位置的像素点，该向量其在裁剪空间中与水平方向的夹角与像素点在裁剪空间的位置有关。而将其直接与透视矩阵相乘，则使得拥有同样主方向，在不同剪裁空间位置的像素点有着相同的投影主方向。因此，原算法会带来如图2的问题。图2与图3渲染了3个不同朝向的圆柱，并沿着圆柱的主方向进行卷积。图2中由于透视问题导致渲染结果不正确：线卷积积分的线条并非沿着物体表面主方向延伸。但若使用3D的线卷积积分，则需要进行体渲染，对渲染管线改动较大。采用本文算法可以规避以上问题，得到图3的效果。

新线卷积算法首先由使用者确定迈进步长与迈进次数。算法流程如下：

步骤1对于每一个像素点，第一步根据有序抖动矩阵与其像素所在位置得到其起始偏移量，通过该点uv坐标对计算好的主方向结构缓冲与世界坐标结构缓冲进行采，之后计算该点的主方向与偏移量的乘积并再加到像素所在世界坐标。

步骤2将所得到的世界坐标位置与投影矩阵相乘，将结果转换为屏幕空间uv坐标，使用此uv坐标对计算好的主方向结构缓冲与世界坐标结构缓冲进行采样，得到新的世界坐标与主方向。

步骤3将主方向与步长相乘，加到世界坐标上，让累计卷积值加上通过uv坐标对当前卷积目标进行采样的值，迈进次数加1。

步骤4若迈进次数未达到规定的迈进次数，则返回步骤2。

通过规定迈进步长与迈进数，可以得到更为风格化的结果。使用较长的步长可以得到软铅描绘的效果，而较短的步长得到的效果更加细腻，类似硬铅绘制得到的效果。

文献［8-9］等在进行素描风格的渲染时，只对白噪声进行了线卷积积分。本文发现，若使用如Perlin噪声，Worley噪声等可以得到一些风格化效果，具体效果在实验部分进行展开。

为了解决空间耦合问题，本文使用uv坐标对噪声贴图进行采样来实现。首先对不同模型设置一个uv比例材质参数。之后在延迟渲染时将每个像素点的uv坐标乘以uv比例材质参数，将得到的结果单独存在一张纹理中。在线卷积积分时，对于每一点的噪声值，用这张纹理中得到uv值去采样一张噪声纹理得到。之所以要使用一个uv比例材质参数，这是因为一些模型因为其使用的纹理数量不同，uv值会出现较密或者较为疏松的情况。通过使用这样一个纹理比例参数来劲调整，使得绘制出来的线条在模型与模型之间有着相近的大小。

2.3 基于艺术导向的素描风格渲染

文献［6，8，12］对素描风格的渲染模拟是从绘制完成的作品中去分析的，而未从艺术家在完成这类作品时为了表现出某些艺术特点而使用了怎样的绘制方式去分析，错过了一些在素描绘制中表现的较为重要的细节。本文从素描绘制期望表现的特点进行分析，对素描风格渲染模拟提出改进。

2.3.1 增强物体表面立体感

素描为了表现出一个面的立体感，往往采用的渲染手法是让面融入场景。为了达到这样的艺术特点，素描绘制的做法是减少边缘，在上色阶段，会将原来作为结构绘制的边缘部分，通过排线的方式，让其通过渐变的方式融入背景，或者物体的较暗的部分，并以此加强边缘两边的亮度对比。即若边缘的一侧，主要表现的物体越亮，那么艺术家会希望边缘的另外一侧就越暗。若主要表现的物体越暗，则艺术家则希望边缘的另外一侧就越亮。

为了达到期望效果，在光照绘制阶段，首先使用alpha通道或者模板缓存标记物体是否是主要表达的物体。因为之后使用到了较大的卷积核，为了提升运行效率，本文对通过将光照计算得到的渲染结果进行下采样。之后将得到的结果进行卷积核较大的高斯模糊，但为了减少计算量，本文并非对于卷积核内所有单位进行全部采样，而是隔一定的像素距离进行一次采样。将计算结果与原像素值进行对比，若原像素值大于该像素值（对应想表现的部分更暗的情况），则结果为原像素值加上使用者设定的希望的对比度大小与两者的差的绝对值的乘积。若原像素值小于该像素值（对应想表现的部分更亮的情况），则结果为原像素值减去使用者设定的希望的对比度大小与两者的差的绝对值的乘积。将得到的结果与下采样前的光照结果进行混合得到最后背景像素值。

图4左边是未经本文处理的渲染图，右边是经过该方法的渲染结果。不难看出，两幅图中，在箭头处所指，物体的边缘两侧（即背景与物体两部分），右图由于进行了风格化处理，使得明暗对比更加明显，这样一种做法在视觉上使得球体更有体积感。

2.3.2 画面处理复杂度的降低以及更加符合手绘的线条

在传统素描绘制中，艺术家往往会使用角度相差不大的线条组对画面进行上色（即素描专业术语：“铺调子”），若使用角度变化较大的线条进行上色，会使得画面处理复杂度较大，而使得画面过于杂乱。在素描渲染中，若直接使用主方向进行绘制，对于复杂模型，由于主方向变化频率高，使得线条角度变化大，导致整体画面处理复杂度过大，使得渲染结果不符合手绘效果。

为解决以上问题，本文使用了两个主方向角平分线的方向作为线卷积的方向。经实验，使用这样的一个方向降低了画面的处理复杂度（processing complexity），计算机美学研究认为美学价值与处理复杂度成反比［24］，处理复杂度的降低让画面更加符合现实到绘画作品的抽象，使其更具有美学价值。并且处理复杂度的降低提高从整体上来看更加符合素描的效果，且由于每个像素点的两个主方向均不存在空间耦合问题，因此作为其角平分线依然不存在空间耦合问题。并且由实验部分可以看出，这种方法在视觉效果上也能表现出物体的结构特征。

求角平分线所在方向很容易整合进本文的算法中。本文并没有分别去求最大法曲率与最小法曲率对应的主方向，再在该基础上求夹角的角平分线，而是在采样8个点的法线射线分成八组计算焦平面时，选择一半的组估计最大法曲率对应的主方向，一半的组估计最小法曲率对应的主方向，再将结果进行最小二乘法回归。

2.3.3 素描三大面的表现

素描中为了表现物体的光影关系，提出了三大面的概念：亮面、灰面、暗面。素描绘制中，应着重加强3个面的对比关系。其中灰面与暗面往往能用光照方程的渲染结果很好地表达。但对于亮面，文献［8］在线卷积积分后对其没有进行处理，使得灰面与亮面的对比感不强。为了表现亮面，本文设置了2个接近1阈值，当像素点的亮度高过较小阈值时，将其亮度进行一定的非线性缩放，使得该亮度在达到第2个阈值时为1。将亮度值高过第2个阈值的像素点也标记为亮度为1的像素点。通过这样的处理，渲染出来的结果也能像手绘渲染一样有与画面其他部分对比较强的亮面，且亮面与灰面过渡平缓。

3 实验效果

3.1 实验环境

使用1 920*1 080的渲染分辨率与InterI9-9990X的CPU与GTX2080的显卡。为了表现这种算法能很好地整合进现有的渲染管线，本文在Unity3D（2019.3.4f1）上进行了实验。并为了得到更高精度的几何缓冲以及存储模型uv信息的几何缓存，实验部分未使用内置的延迟渲染管线，而是使用了Unity3D的可编程管线（SRP）重新实现了延迟渲染。

3.2 实验效果

3.2.1 主方向实时估计效果

对2个图形学常用模型的主方向进行估计，并分别计算其主方向，并将结果其渲染到屏幕空间上，与现有算法进行对比。为方便读者比较，本文将主方向单位向量的绝对值作为像素点的颜色。其中本文算法与文献［6］的结果算法经过了文献［6］使用的滤波。其中，图5为文献［3］中算法，图6为文献［6］中算法，图7为本文算法。表1为每种算法计算所的时间，表2为以文献［3］算法（图5）为基准，对图6与图7分别计算峰值信噪比。可以看到，本文的算法每一帧渲染时间虽然略高于文献［6］的算法，但是鲁棒性较强，且不会出现如中部分因为估计时解二次方程判别式为0带来的黑色区域。通过对比峰值信噪比，本文算法比文献［6］的算法在估计值上更加准确。相比于文献［3］的算法，无需大量的预计算时间。

表1 主方向估计所需时间

表2 本文算法、文献［6］算法与文献［3］算法计算的峰值信噪比

3.2.2 线卷积积分

将文献［8］使用的文献［10］的线卷积积分与本文提出的改良后的线卷积积分算法的渲染结果进行对比。图8为文献［8］的算法，图9为本文的算法。每组中，从左到右分别是卷积长度为10、20、40、60的结果。表3为每组中不同卷积长度每一帧渲染所需时间。

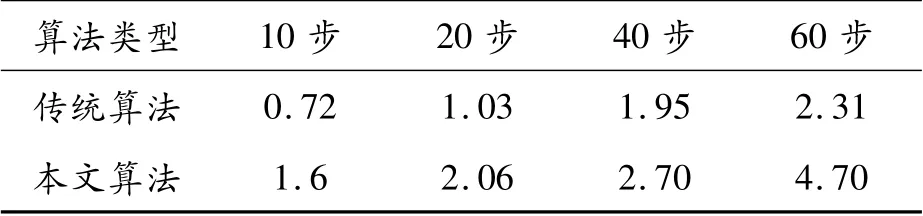
表3 线卷积所需时间 ms

从以上算法中可以看出，本文提出的线卷积算法虽然在相同步数下性能低于传统算法，但本文的算法在10步时有着与原方法60步的效果，并且透视正确。表明了本文的线卷积算法能用较低的步数获取原方法较高步数的效果，且近似效果下，本文算法的10步需要的每一帧渲染的时间1.6 ms低于原方法60步所需的2.31 ms。

3.2.3 画面处理复杂度的降低

为表现相比于直接使用主方向作为线卷积的方向，使用本文算法的主方向的角平分线能降低画面的处理复杂度而进行实验。为了定量计算处理复杂度的降低，本文使用了文献［24-25］中对美学价值处理复杂度定量计算的指标，即将图像采用有损压缩算法（本文使用JPEG压缩算法，即DCT变换），之后通过均方根误差除以压缩率来计算图像的处理复杂度。分别将两个模型的主方向以及主方向间的角平分线的方向与透视矩阵相乘，将得到的方向向量结果转换为标量角度并缩放到纹理像素的取值范围。图10为计算得到渲染结果，其中左边为直接使用主方向，而右图为使用主方向的角平分线。之后分别对每一组计算文献［24-25］中的指标（使用50%的压缩率），结果如表4所示。实验结果表明，使用角平分线相比于直接使用主方向能够降低画面的处理复杂度。

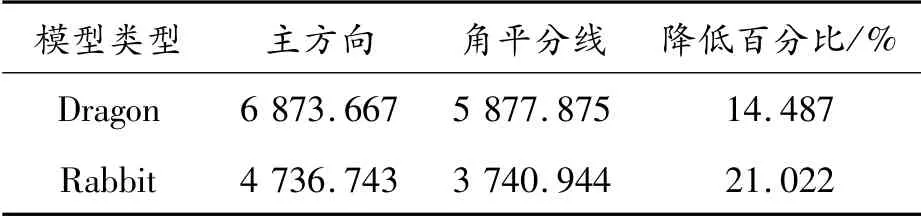
表4 图10中每组画面处理复杂度的降低比例

3.2.4 不同类型噪声的风格化卷积效果

分别使用白噪声、Perlin噪声以及Worley噪声进行线卷积积分。其中文献［8-9］使用到白噪声如图11，Perlin噪声如图12，Worley噪声如图13。为方便对比，未与光照进行混合。经过对比可以发现，使用白噪声进行卷积，得到的结果较为细腻，像是由硬度较高的铅笔绘制出。Perlin噪声轻线条与重线条的区分较白噪声更为明显，像是由硬度适中的铅笔绘出。Worley噪声卷积后得到的结果轻线条与重线条区分十分明显，像是用软铅绘制而成。实验表明，使用不同噪声进行卷积，会带来不同的风格化效果。

3.2.5 空间耦合性

为表明本文算法有较强的空间耦合性，图14对通过本文算法渲染的模型的一系列角度进行观察。不难发现，随着视角位置的变化，模型身上的线条位置没有发生变化。实验表明，本文算法具有较强的空间耦合性。

3.2.6 间隔一定距离采样对性能与效果的影响

为表现本文在2.3.1节中，使用间隔一定距离采样的算法对性能与效果的影响，本节分别对73*73的卷积核全部采样，间隔不同像素距离的采样效果以及渲染单帧所需时间（运算量）进行分析。渲染效果如图15所示（从左到右，从上到下依次为全部采样，间隔2、4、6像素进行采样），单帧渲染时间如表5所示。可以看出，全部采样以及间隔一定像素进行采样对渲染效果无明显影响，而性能上相比于全部采样，间隔6像素进行采样每一帧节省了186.9 ms。

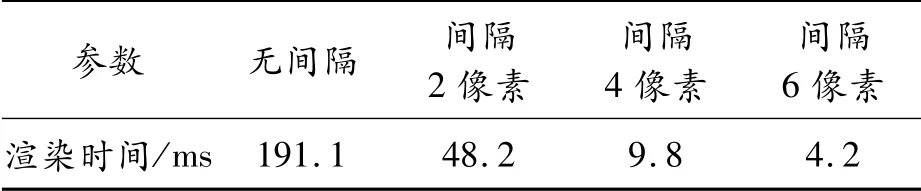
表5 间隔一定像素距离的每帧渲染所需时间

3.2.7 素描风格渲染

本节将素描渲染得到的整体效果，与按照文献［8］中的线卷积方式，以及其卷积方向的选择得到的效果进行对比。按照文献［8］中的线卷积方式，以及其卷积方向的选择得到的效果如图15所示，按照本文算法渲染得到的结果如图16所示。

通过对比，在线条描绘上，图17中，通过结构张量对光照结果进行分析，对主方向表现不明显的脐点，如平面或球体，按照其亮度变化的方向进行卷积，使其也有较为适合线条表达其形状特征。并且对主方向表现明显的物体，使用了多个方向进行叠笔。并且运用了本文的透视正确的线卷积积分，在表达物体的形状上更为准确。而图16文献中算法因仅考虑了主方向作为其卷积方向，使得其对于主方向不明显的脐点只能用固定的方向进行卷积，并且存在透视错误的问题，使得线条无法很好地表现出物体的形状特征。

图17 中，通过对高于一定阈值的像素点的筛选形成了亮面。这种做法加强了画面灰部与亮部的对比，并且通过对背景进行处理，加强了物体的立体感，使得整体效果更贴近手绘素描效果。而图16中，该算法没有考虑物体与物体之间的关系，且未根据素描表现效果进行风格化处理，使得其表现效果不如本文的渲染结果。

4 结束语

本文提出一种更具鲁棒性的实时主方向估计，以及一种效率更高且透视正确的线卷积积分。通过将这两种方法，并结合艺术导向的处理，得到符合美学且实时的素描渲染结果。实验结果表明，这种算法比传统素描绘制算法能更好地表现手绘素描效果，且有着较广泛的适用性。由于主方向可以很好地表现物体的形状特征，因此后续考虑将这种鲁棒的实时主方向估计应用到其他风格化渲染（如油画等）上。